高中物理心理建构教学法的应用

四川省宜宾市南溪一中 邓第宅

一、可解性原则

由于受所能采用数学工具的限制，高一年级运动学是从研究匀变速直线运动开始的，首先是在加速度概念的基础上，引进了两个公式：

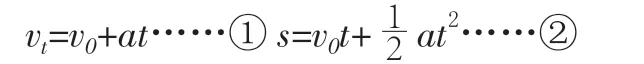
同时给出了两个推论：

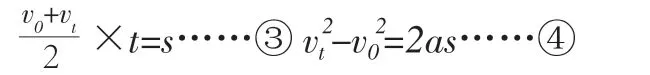
之所以把③和④叫推论，是因为它们可以从①、②两个公式中推导出来。其实这四个公式，只要肯定任意两个，都能把其他两个公示推导出来。然而作为一个逻辑系统，匀变速直线运动所涉及的量，包括初速度、末速度、时间、位移和加速度，已知两个互相独立的方程，只需要告诉三个物理量就能把余下两个未知量计算出来。按已知条件的不同组合，符合可解性要求的题目一共能编十种题（C53=10）。这就是匀变速直线运动的基本数量关系，也是我们从理论上把握这类问题分析方法的逻辑基础。

二、最简思维原则

上述十种题都可以在上列四个等式中任取两个联立起来，计算出结果。只是为了寻求最简算法，有必要进一步研究选择方程的原则。

观察上面四个等式，它们都分别联系着四个物理量。如果题目给出三个已知量，再设定一个求解量，正好与某个等式中的四个量相对应，该等式就成了计算求解量的一元方程，解此方程就是该题目的最简算法。因此，寻求匀速直线运动问题的最佳算法，有两个思考点：第一，题目是否告诉了三个已知量，据此判断题目是否可解；第二，根据题目与哪四个量有关，或者与哪一个量无关，据此确定采用哪个方程计算量最小。具体的选择原则是：与位移无关的问题采用方程①；与末速度无关的问题采用方程②；与加速度无关的问题采用方程③；与时间无关的问题采用方程④。有了这套符合最简思维原则的思路，学生即可有效在正确理论指导下实践。

三、逻辑全覆盖原则

如果因为加速度改变，形成两个不同的运动阶段，前阶段的末速度就是后阶段的初速度。这两个运动阶段一共涉及九个量，有四个相互独立的方程，只需再告诉五个量即可求解。在这五个量中有三个同属一个运动阶段，该阶段独立可解。另一个运动阶段首先计算出连接点上的速度，使其拥有三个已知量，成为可解运动阶段，这样的分析思路，显然是最简捷的。

但是，以上分析是否对多运动阶段的可解题目实现了完全覆盖？还是说没有独立可解运动阶段的题目，运动情况将无法确定？按照可解性原则推理，如果在两个运动阶段的基本等式之外，给出涉及两运动阶段的等量关系，比如，告诉两段位移之和或者两个阶段的总运动时间等相关条件，就可以减少一个已知量。在九个元的系统中，知道四个已知量，由五个方程解五个未知量也是可以的。这就是没有独立可解运动阶段的多运动阶段综合题，只有把各种情况都研究透了，才能实现对直线运动问题的逻辑全覆盖。

四、可操作性原则

例如，题目告诉某质点以大小为v0=3m/s 的初速度，沿直线轨道做匀加速运动，当位移达到s1=10m 以后，加速度减半。在往后的t2=2s 时间内,发生的位移是s2=16m，求前后两运动阶段中的加速度。

此题的可解性显然是成立的，其结果应该是以下五元二次方程组的解，其中v1和v2分别代表两个运动阶段的末速度。

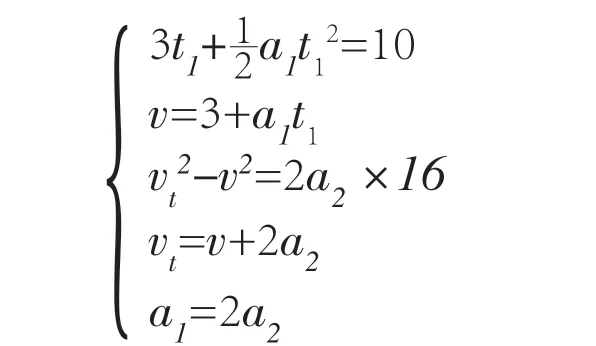
可是学生要在要求的考试时间里解出这个五元二次方程并非易事，更不用说大多数高中生并没有掌握这类题型的逻辑关系，即使有的学生想到要用方程组来求解，但是乱列几个等式，也许不足五个，也许互不独立。此类题的评分标准是在五个方程之后写上“解之得……”字样，然后进行正确演算。因此，对于这类题目的研究不能停留在可解性的判断上，只有让学生掌握切实可行的计算方法。这就是心理建构教学法的可操作性原则。

为了帮助学生克服在考试中不能迅速解开五元二次方程组的困难，最好的方法是找到直接得出连接点上的速度的一元方程，这个方程的原型就是相关条件。设连接点上的速度为，配合前后两个运动阶段中的已知量，表示出相关条件中的有关物理量，这些表达式至多是二次式，然后代入相关条件，即可获得的一元方程。

以上是以直线运动为例，阐述了心理建构教学法的原理。将这些原则推广到整个高中物理教学中，诸如运动力学、电磁学以及相对论和量子力学，甚至是推广到各门自然科学的教学领域，都会卓有成效。学科之间的教学内容虽然不同，但都属于公理化体系，是符合逻辑的，因而可以沿着可解性和可操作性思路，从题型和方法的复杂网络中厘清线索，让每一道可解题的最佳解法都是程序化推理的结果。这条线索还能引导教师找到改善学生心理结构的关键，制定出提高学生思维品质的训练方法。有了这些研究成果，笔者的课堂教学变得别开生面。高中物理教学主要内容是学科知识的理论体系以及可解题型的逻辑构成，只要能展示寻求解题方法的思想过程，例题不必多，但凡讲必透，学生作业少，但要在正确理论指导下进行训练，训练的目的是巩固理论知识。

建构主义是继存在主义之后流行于欧美的哲学流派，最初出现于皮亚杰对儿童心理成长过程的研究中，强调儿童心理发展的阶段性，认为思维能力的提高是通过同化和顺应两种不同的作用方式，在不断改善心理结构的过程中实现的。心理建构教学方法并不是抽象的哲学理念，而是实实在在的教学原则。为了提升高中生的思维品质，学习知识固然重要，但是在领会学科知识逻辑结构的基础上，形成正确有效的思维模式更重要，这才是智慧。

在学科教学中，有一种错误观念叫“熟能生巧”，以为应用知识解决实际问题的能力，可以通过反复训练达到炉火纯青。智能的特点是理论指导实践，科学知识是对客观世界的原则说明。客观世界变化万千，应用知识解决问题，存在选择理论和构想方案的问题，智能行为必须自始至终在意识的干预下实施。不过人的能力是多方面的，一些技能经过反复训练的确能够熟练掌握，但也必须达到无意识操作的水平。如计算机操作技能、体育运动技能以及各种专业技能都需要进行反复训练，掌握技能标准，达到在无意识状态下操作。任何技能一经掌握，原则上是不会忘记的，所以技能是一般高等动物赖以生存的主要能力。然而动物的技能是一种行为习惯，只需模仿就能形成，叫“习得性技能”。而人必须理解技能原理，在理解的基础上反复训练，才能成功，叫“知识型技能”，或者简称“技术”。花样滑冰就是这样的技术，运动员必须懂得在冰面上高速运动时保持平衡的原理，知道什么时候打开和收起手臂，控制身体的旋转速度，在正确理论的指导下进行反复训练，才能达到娴熟的水平。而运动员在参加比赛的时候，却不必有意识地控制每一个动作，只需跟随优美的旋律舞动就能让整套动作天衣无缝，尽展青春美丽。运动员这时的每一个动作，已经成了行为习惯，这才是“熟能生巧”。可是智能不是技能，不能在无意识状态下实施，不会“孰能生巧”。智能之巧源于对学科知识的深刻理解，也来自有效的思维定式。某些心理学家过分夸大无意识在认识发展中的作用，甚至说人的意识只是“冰山的一角”，胡诌大多数科学发明都是在无意识中实现的“事实”，为在教学中以灵感代替逻辑，以训练代替理解，推行所谓“精讲多练”的题海战术提供理论依据。

心理建构教学法反其道而行之，主张严格区分智能和技能，强调以学科知识的逻辑结构为出发点，在对基本模型思维过程进行形式化处理的基础上，研究可解性拓展题型及解题方法，引导学生反思自己的思想过程，改善心理结构，最终针对各类问题形成正确有效的思维定式。这种教学方法得到曾经的学生肯定，他们说：“二三十年过去了，高中物理题几乎都不会做了。可是当年在物理课上学到的研究方法，伴随着自己走向成功，是一辈子都不会忘记的。”