逢山开路 遇水搭桥——妙用三角参数解题

江苏省丰县民族中学 (221700) 高成功

“掌握数学就意味着善于解题”，对于数学题有时解法和思路会很丰富.解题时要做到“逢山开路，遇水搭桥”,完善解题过程,让解题变成一种追求和境界.引入参数通过换元完成解题的方法很多，因三角函数公式多、变换活、思路广以及正、余弦函数的有界性，为问题的解决带来极大便利. 三角换元法也称为三角代换、参数换元法.本文谈谈巧妙引入三角参数进行换元在求解问题中的应用,以期对提高学生的解题能力有所裨益.

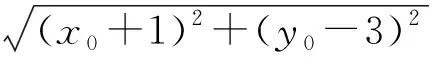
分析：(1)过点P的直线有无数条，讨论直线斜率是否存在从而引入参量进行解题是一种常规思路；(2)结合解题经验利用点C的轨迹是一个圆，从几何的角度也可以解决该题;(3)由于圆、直线等具有一种三角参数方程式，有时选用便于突破重围，起到出奇制胜的良好效果.

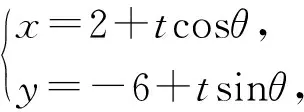
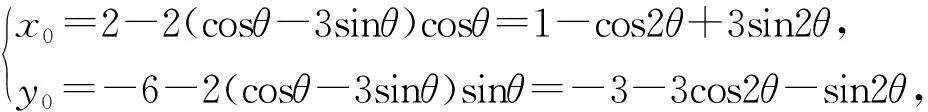
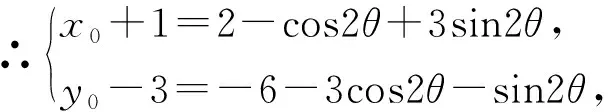
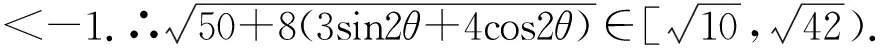
评注：通过引入参数换元实现了代数和三角的转化，使思维处于“山穷水尽”之时，能神奇地开拓“柳暗花明”的局面.

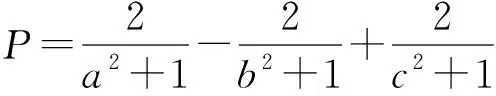
分析：这是一个三元未知量求最值问题,消元法此时也不易于问题的解决.根据式子的结构特点考虑引入参数使用三角换元法.

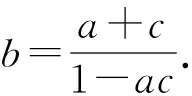
评注：三元最值问题，观察结构特点，联想知识内在联系.引入变量代替某个可以看成一个整体的复杂式子,进而使问题简化.引入三角参数是中学解题中常见的换元技巧,它主要利用已知代数式与三角知识的联系进行换元.通过联想类比,将代数形式转化为三角形式,再利用三角函数的性质,巧妙地实现解题.

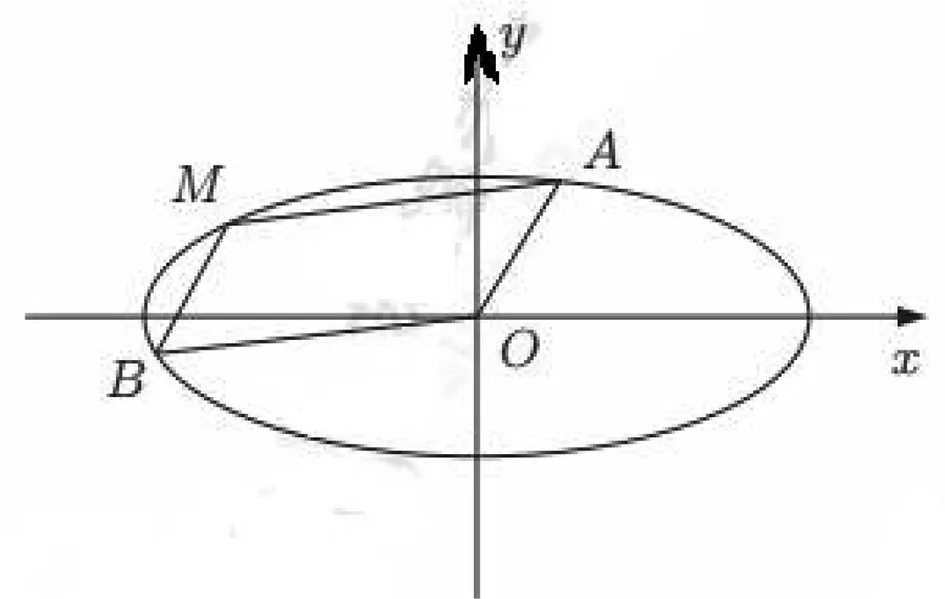
图1

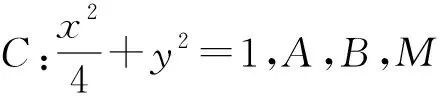
分析：本题常规解法是为了求直线斜率通过设出直线斜率的方法解题.通性思路为设出直线AB的斜截式、联立方程组，运用韦达定理；结合平行四边形下的共圆条件得出直角进而利用垂直条件、以及点M在椭圆上，从而实现两个未知量组建两个等量关系式的目标,问题由此得解.

下面通过设点法(引入三角参数法)来解题.

解：设A(2cosα,sinα),B(2cosβ,sinβ),其中α,β∈[0,2π).显然直线AB的斜率存在，即2cosα≠2cosβ.由于四边形AMBO是平行四边形且A,B,M,O四点共圆，可知四边形AMBO为矩形，由OA⊥OB可得4cosαcosβ+sinαsinβ=0.易知M(2cosα+2cosβ,sinα+sinβ),将点M代入椭圆方程整理得

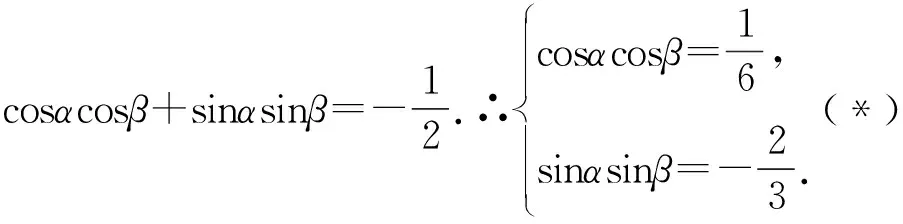
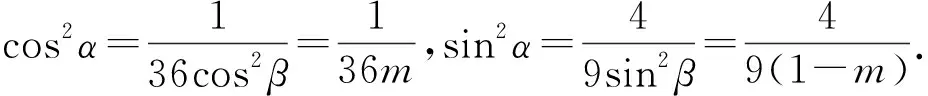
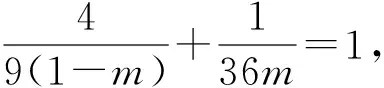
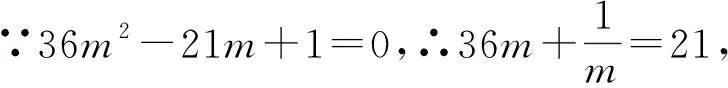
评注：三角参数介入解题，变形技巧是关键；引入变量m设而不求、机动灵活.学习数学，不仅要学习已有的技巧，更要培养良好的观察能力，从整体看，从局部看，从不同角度去看，发现问题的特点，挖掘其中的联系，自己创造技巧，而这种观察能力，正是素养的一部分，应当逐步养成.

总之,引入参数结合三角函数性质解题是一种非常重要的数学思想方法,一些看似无从下手的题目,巧妙引入参数进行换元,往往会达到事半功倍的效果.