横看成岭侧成峰，远近高低各不同——一道模考题的讲评历程及变式探究

江苏省常州市田家炳高级中学 (213000) 徐 颖

高考模拟题的设计力求情境熟悉，切入口多，方法灵活多样，其中填空题的设计以短、平、活为主，能更好地体现学生对知识的掌握程度和应试能力，研究价值很高. 本文通过对2020年苏锡常镇高三数学一模卷14题答题情况的调研，分析学生思维受阻的原因，试图寻找教学中存在的问题，进而提高教学的有效性.

1.试题

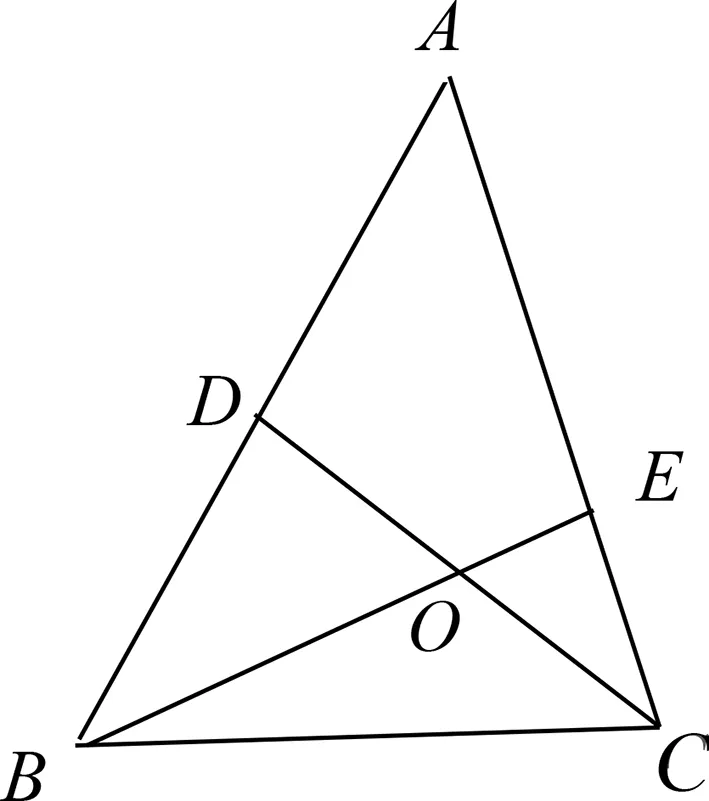
图1

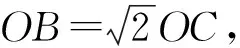
本题考察解三角形、平面向量的运算、最值问题.考查学生等价转化、数形结合等数学思想方法和逻辑推理、直观想象等数学素养，其背景常规，综合性较强，区分度高，涉及的知识点也较多，对学生化归能力要求较高.

2. 教学过程

2.1 横看成岭侧成峰，远近高低各不同

(在点评前，老师要求学生先自行订正，找出问题)

教师：那位同学愿意分享一下解题思路？

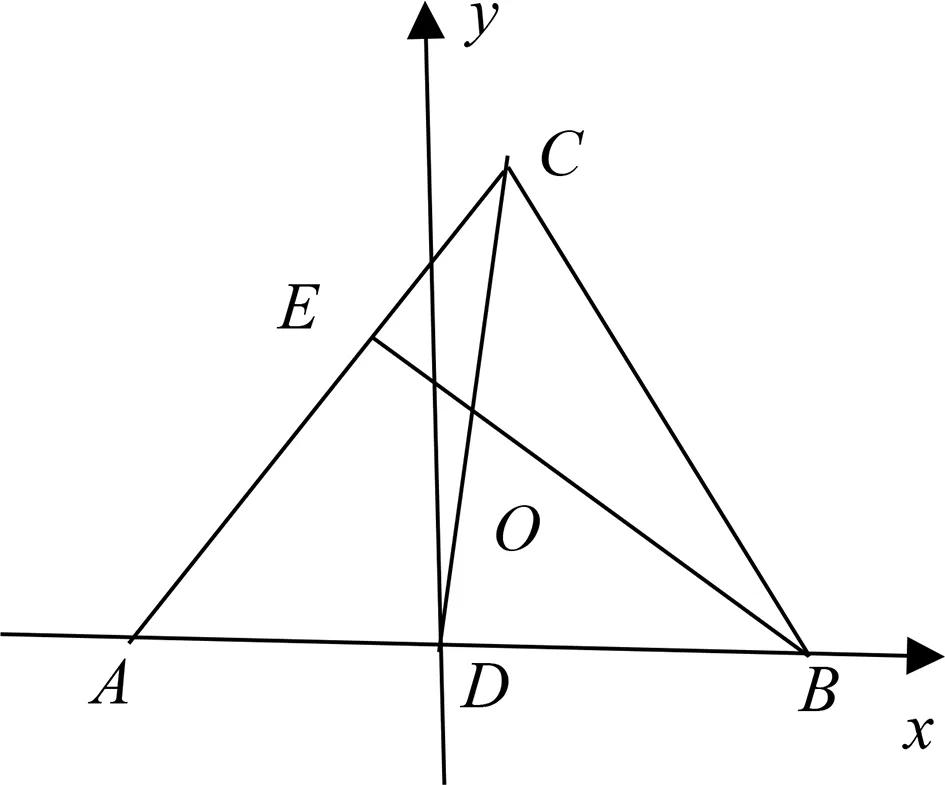
图2

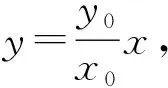
图3

学生2举手示意：关于点O的位置，我认为可以利用平面几何知识，如图3，取AE中点T,连接DT，由于E,T为AC的三等分点，故E为TC中点，由BE//DT可知O为CD中点.

教师：学生1采取建系，这是将代数问题几何化的一种常见方式，非常棒！我很欣赏学生2的确定O点位置的两种方法，利用几何法抓住图形的特征，太赞了，让我们茅塞顿开，也学会了找线段定比分点的方法，他发现了这道题目的第一个本质，这要求我们有灵动的思维，多从图形中发现动中有定.接下来，大家思考如何表示三角形面积？

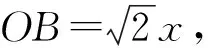
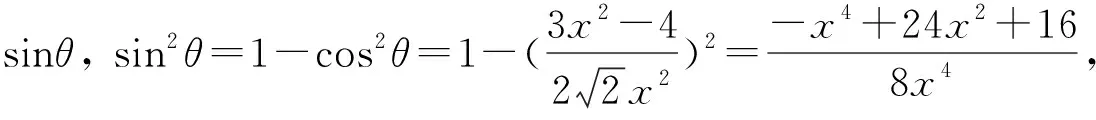
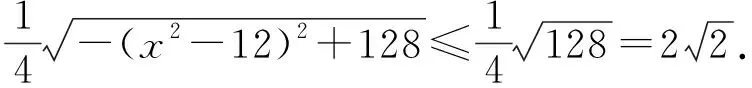
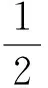
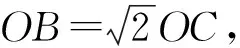
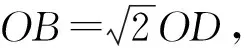
(下面掌声一片！)

教师：学生5，6的解法又让我们眼前一亮，将问题与轨迹思想联系，揭示了这道问题的第二个本质. 前面提到的三点共线定理和阿波罗尼斯圆其实都是课本上例题或练习题，看来在最后复习阶段我们还要回归课本，夯实基础，掌握经典模型.

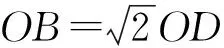
2.2 等闲识得东风面，万紫千红总是春

针对问题的不断深入，在寻求解法的同时，领略考题的本质，挖掘其深刻内涵，作出一些必要的延伸和拓展，充分发挥试题的功能和作用.

图4

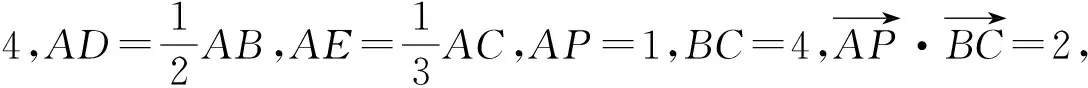
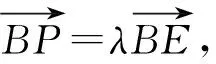
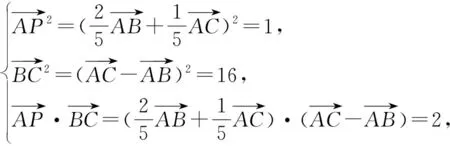
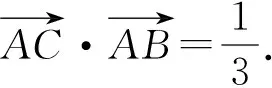
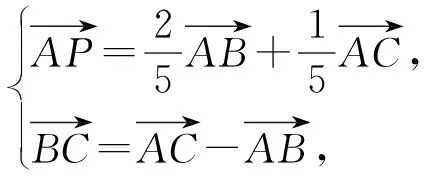
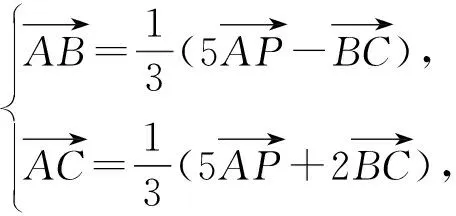
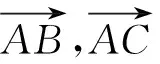
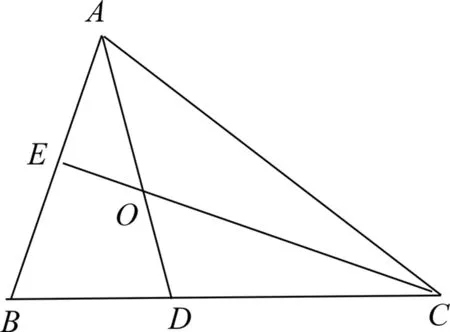
图5

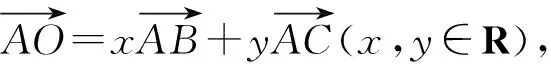
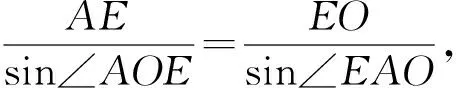
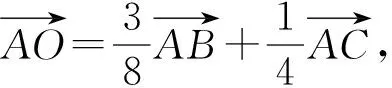
点评：三角形中关注一些小结论，如上，利用角平分线定理能更快得到D点位置.

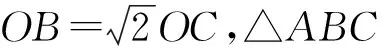
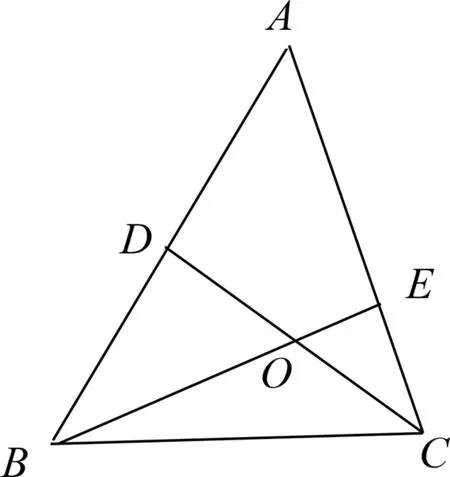
图6

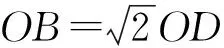
3.教学启示

3.1 解题教学应注重学生的参与，构建动态教学

在高三复习过程中，时间紧，任务重，有的教师急功近利，追求大容量，往往只提解题思路，展示正确的解题方法，很少顾及学生的真实感受，学生自主探究的机会不多，缺少思维过程，只会死记套路. 告知学生，他们会忘记；板演给学生看，他们会记住；本题的一题多解，不是教师预设好硬塞给学生的，而是通过生生互助，师生互动，在一个动态过程中形成的产物，，让学生参与其中，亲经历，真学习，体验数学的发现与创造，获得解题的成就感，提升数学素养.

3.2 解题教学应注重挖掘课本例习题的潜在教学功能

本题的两个切入点就是三点共线定理和轨迹思想，在必修4向量章节和必修5直线与圆章节都有涉及(课本例题或习题)，我们知道课本例题、习题常常是高考命题的生长点，那么怎样具体实施教学才叫活用教材？只有教师在平时的教学过程中，认真钻研，精心设计课堂教学，做到以少胜多，举一反三，帮助学生实践从“一题多解”到“多题一解”的跨越，不在于解法的多样性，而应该挖掘数学本质，形成通性通法，扩大解题的“武器库”[1]，这样才能有效培养学生的数学能力,实现真正减负.