对 “f (x)与f ( f (x) )有相同值域” 问题的思考

四川南充高级中学顺庆校区 (637000) 张小丹 李 婷

一、试题呈现

设函数f(x)=x2+2ax+a，若函数f(x)与函数f[f(x)]的值域相同，则实数a的取值范围为.

第一步：分析f(x)的单调性与最值，易知f(x)在(-∞,-a)上递减，在(-a,+∞)上递增，f(x)min=f(-a)=a-a2，∴f(x)的值域是[a-a2,+∞).

第二步：换元分析两函数.设t=f(x)，则f[f(x)]=f(t)，函数f(t)在t∈(-∞,-a)上递减，在t∈(-a,+∞)上递增，则y=f(t)(t≥a-a2)的值域也是[a-a2,+∞).

图1

第三步：问题求解.设y1=f(x),y2=f[f(x)]，则y2中的f(x)等同于y1在中的x，要y1,y2两函数具有相同的值域，只需y2中的f(x)与可以取到y1中的x的所有的值，即函数f(x)的值域能取遍其定义域中的一切实数.从而由图1可知a-a2≤-a， 解得a≤0或a≥2 .

事实上，我们可以把此题的情况进行推广，得到如下结论：

二、归纳结论

结论1设函数f(x)在其定义域上先减后增，极小值点是x0，f(x)的值域为[f(x0),+∞)，若f(x)与f(f(x))有相同值域，只需f(x0)≤x0.

结论2设函数f(x)在其定义域上先增后减，极大值点是x0，f(x)的值域为(-∞,f(x0)]，若f(x)与f(f(x))有相同值域，只需f(x0)≥x0.

三、结论应用

例1设f(x)=lnx-x+a，若函数f(x)与f[f(x)]的值域相同，则实数a的取值范围为.

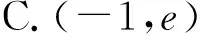
四、完善结论

若f(x)在其定义域上单调，且f(x)与f[f(x)]有相同的值域，那么参数的范围怎么求呢？

分析：设t=f(x)，y1=f(x),y2=f(t)，要使f(x)与f(t)的值域相同，只需t能取遍x能取到的数，即f(x)的值域能取遍其定义域中的一切实数.

结论3设函数f(x)的值域为R，若f(x)与f(f(x))有相同值域，则f(x)的值域能取遍其定义域中的一切实数，即f(x)的定义域为其值域的子集.

例4已知函数f(x)=ex+ae-x+2，若y=f(x)与y=f[f(x)]的定义域相同，则a的取值范围是( ).

A.a<0 B.a≤-1

C.0