“先学后教”理念下的校本作业开发与实践*
2021-01-28福建省厦门实验中学361116黄耿跃福建省厦门第一中学361000李蓉蓉
福建省厦门实验中学 (361116) 黄耿跃福建省厦门第一中学 (361000) 李蓉蓉
国家中长期教育改革和发展规划纲要要求:“减轻中小学生课业负担,学校要把减负落实到教育教学各个环节,给学生留下了解社会、深人思考、动手实践、健身娱乐的时间.”但受应试教育影响,有些教育工作者急功近利,导致以知识落实为主的作业成为教师抢占学生课后时间的重要武器,以布置大量作业,换取学生成绩提高为手段,造成学生对作业的厌烦,甚至厌恶,使一部份的学生成绩反而更差、跟不上.
笔者所在学校,厦门实验中学是一所新办校,学校在开办时就设计好校本作业开发与实施方案,要求学生统一不订阅教辅材料,每天的作业都由老师自己选题、组题.办学7年来,高考取得令人瞩目的成绩,这与学校制定的“五个四”校本作业体系的办学指导思想是密不可分的.本文是笔者站在数学科的角度,就如何开发、实施”五个四校本作业“谈谈自己的一些做法.
一、“五个四”校本作业概念界定
“五个四”校本作业:指四案、四精、四必、四合、四查.
1.四案:指学案、 作业、 课练、 周练.学案是新授课课前发给学生,由学生自主阅读课本并完成学案内容,内容主要包括“知识梳理、重难点问题记载、自主检测、总结反思” 四个模块,达到预习新知的目的.作业与学案相配套,是课后对学生所学知识的巩固练习.学案与课后作业穿插进行,实行小单元教学法.
2.四精:指精选、精练、精讲、精评.四案中的问题老师要先做一遍认真精选,题量控制,让学生跳出题海,达到精练的目的;通过学案引导学生先学先做,在学生先学的基础上老师再精讲,学生会的不再讲;课后作业也是学生先做的基础上,教师从知识重难点和学生易错点两方面剖析题目.四精是四案质量的保障.
3.四必:指必发、必收、必改、必评.对四案中的校本作业,学案要提前1至2天发到学生手中,让学生先学先做,老师收改后再进行施教;课后作业、周练也是让学生先做,老师收改后及时讲评;课练应当天批改当天发还学生手中,让学生及时订正,及时强化知识点,第二天讲评.四必是实施四案校本作业的重要过程.
4.四合:指与作业的八个要求(统一布置、分层要求、先做后讲、全批全改、个别辅导、点评到位、人人过关)相结合、与五步学习法(预习、上课、作业、复习、总结五个环节)相结合、与考点教学法相结合、与家教式辅导相结合.四个结合是四案校本作业细化层面的具体内涵.
5.四查:指查四案质量、查校本作业落实情况、查存在问题、查效益.四查是对四案校本作业补漏提质的重要环节.
二、校本作业开发与实施
零点问题是高考中的重要考点,也是高考的难点,所以学生只有通过先行做题,再听老师讲解,最后再进行类题训练,才能达到巩固、强化,真正理解消化、掌握技能的目的.按照我校校本作业的开发与实施理念,高三年总复习时,对零点存在定理这一重要知识的复习安排,我们会先在学案中安排如下两道解答题,目的是让学生初步学会如何利用零点存在定理解决问题,特别是突破如何取点的问题.
题1 已知函数f(x)=ex-ax(a∈R)存在两个零点,求实数a的取值范围.
题2 已知函数f(x)=lnx-ax(a∈R)存在两个零点,求实数a的取值范围.
设计意图:两个常见的超越函数ex,lnx与一次函数的简单组合,是学生熟悉的函数,与高考试题的命题思想是相吻合的,让学生拿到作业感到亲切,有想做、敢做的冲动.同时,两道题目蕴涵丰富的思想方法,可全面训练学生利用导数研究函数的单调性,零点存在定理中端点值的取法,不等式的切线放缩法及分类讨论思想、数形结合思想等.
下面就如何利用题1揭示问题本质,进行精讲、精评、精析.
第一步,对函数进行求导,利用导数研究函数的单调性.∵f′(x)=ex-a,∴f′(x)>0⟹x>lna,f′(x)<0⟹x (师:结合函数的图象特征可知f(lna)为函数的极小值,要使函数存在两个零点,则必需满足f(lna)<0,从而可求得a>e,但要注意a>e是结论成立的必要条件.所以,必需在lna的两侧各找到一个点的函数值大于0,才能说明a>e是所求的范围.) 第二步,利用零点存在性定理,找端点的函数值正负.∵f(-1)=e-1+a>0, (师:显然,只要x<0的任意一个数,都能使f(x)>0成立,所以这个点是比较好取的,结合函数的单调性,也就意味着在区间(-∞,lna)上必存在唯一的零点.) 综上所述a>e. 题2的讲解与题1的讲解类似,限于篇幅,请读者自行完成. 在课练和周练中,我们再选2道高考题变式,目的是让学生通过听完老师的讲解,通过自己的领悟,利用所学到的思想方法,进一步解决如下两道问题.因为课练和周练都是限时训练,有时间限制,所以通过课练或周练的形式,可以真正检测学生的学习效果. 题3 (2017年全国Ⅰ卷理科变式)已知函数f(x)=ae2x+(a-2)ex-x,若f(x)存在两个零点,求实数a的取值范围. 题4 已知函数f(x)=(x-2)ex+a(x-1)2(a>0),若f(x)存在两个零点,求实数a的取值范围. 下面就如何利用题3揭示问题本质,进行精讲、精评、精析. (师:这种取点判断函数值的正负问题,一般情况下,左右两边有一个数是比较好取的,可以通过观察得到,而另一边的点一般是带有参数的点.) 综上所述,当0 题4的讲解与题3的讲解是类似,限于篇幅,请读者自行完成. 我校“五个四”校本作业实施3年来,数学组的成绩取得较大的进步,从厦门市历次的质检和3次省质检成绩可以佐证.如果不是实施校本作业,对函数零点存在定理的复习,我们也无法根据学生的实际情况,编写四道有针对性的问题展开复习,这是真正体现“因材施教”的教学原则,真正体现“因地制宜”的教育思想.先学后教的理念在“五个四”校本作业得到完美诠释,有利于真正培养学生自学能力.因为学生长期以来都是带着问题在学习、在听课、在反思,这对提高学生分析问题、解决问题的能力是润物细无声的.由于“四案”的作业量始终保持在12道题,这种题量对学生来讲是最适合的.优秀生在完成作业后,可以腾出时间自主安排,进行总结、反思、梳理知识,中等生在一节课的时间内,基本可以完成作业;后进生也可以完成80%,可以说“四案”校本作业是普遍受到学生的欢迎,也是能有效激发学生学习数学的兴趣和热情的.

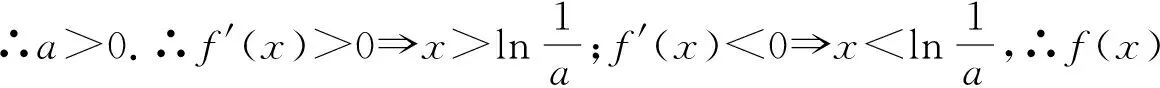



三、感悟
