格基规约技术在混合预编码中的应用*

王 曼

（喀什大学，新疆 喀什 844000）

0 引言

在大规模MIMO 系统中，基站配置上百根天线。若采用全数字预编码，则每根发射天线与一个射频链路相对应。这不仅增加了系统复杂度，还使硬件实施成本更大。如何减少硬件成本是研究的热点，而混合预编码技术可以通过降低射频链路数来达到减少硬件成本的目的。相比传统混合预编码技术，自适应混合预编码[1-5]可进一步简化系统的复杂度。

格基规约技术是将原来的一组“基”根据某种准则变换成另外一组新的基。新的基向量具有更好的正交性，而当基向量正交时，在线性滤波时没有噪声的增强，因此此时的ZF 检测可以达到与最大似然译码或球形译码一样的差错性能。文献[6]提出的LLL 算法能够显著降低格基规约算法的复杂度，使得该技术广泛应用于信号处理方面。但是，LLL 格基规约算法仅限于对实基矩阵进行约减。当用于复值基矩阵时，不仅会使基矩阵的维度增加一倍，也会大大增加运算复杂度。文献[7]提出了CLLL 格基规约算法。这种算法与LLL 格基规约算法相同，但可以直接对复值矩阵进行格基规约，且运算复杂度只有LLL 格基规约算法的一半左右。

本文中所用符号说明如下：(·)T和(·)H分别为矩阵的转置和共轭转置||·||F和|·|分别表示取F 范数和取模；tr(·)是求迹；ℜ(·)和ℑ(·)分别表示复数的实部和复数。

1 系统模型

在大规模MIMO 系统中，假设在基站完全已知信道状态信息的情况下，基站配备了N根天线，接收端有K个用户，每个用户只有一根天线。传统的混合预编码需要NK个模拟移项器（Analog Phase Shifter，APS）和N个加法器[8]，而自适应混合预编码仅需N个APS，且不再需要加法器，大大降低了硬件成本和系统复杂度。自适应混合预编码的结构如图1 所示。

图1 自适应混合预编码的结构

K个用户的接收信号可以表示为：

式中，H∈CK×N是基站和所有用户之间的信道矩阵，F=[f1f2…fk]∈CN×K是模拟预编码矩阵，其中fi=[fi1fi2…fik]T∈CN×1，W=[w1w2…wk]∈CK×K是数字预编码矩阵，X∈CK×1为发送信号，n=[n1n2…nk]T是加性高斯白噪声，是k个用户的噪声。为保证总发射功率恒定，满足：

式中，P是基站的总发射功率，IK为单位矩阵，数字预编码矩W应满足归一化条

1.1 模拟预编码矩阵

混合预编码的设计分模拟和数字两部分。先设计模拟预编码矩阵F，F是通过信道矩阵H或预定义码本设计的，以此得到下行链路的等效信道矩阵。对于自适应网络而言，在射频链和移相器之间添加自适应网络。与传统的预编码比较，它不再需要射频相加器，由自适应连接网络和N个模拟移相器组成模拟预编码矩阵[8]。自适应网络决定了此矩阵中的非零元素，模拟移相器确定了非零元素的相位，所以需同时满足以下限制条件：

条件a 确保了每个射频链路由M个模拟移相器与M根天线相连，这里的M=N/K，其值为整数；条件b 能够确保每根天线仅通过一个模拟移相器与一个射频链路连接。由条件a 可知，模拟预编码矩阵F中的每列元素仅有M个不为0。下面确定M个不为0 的元素的位置。

由于H=[h1h2…hk]T，其中hi=[hi1hi2…hik]T，可通过来确定fi。fi中仅有M个有效值，若要满足max{hi fi}，那么fi中的M个有效值所在的位置应和hij0的位置相对应（hij0分别为hi中振幅最大项），且这M个元素分别取hij0的负相位，fi中的其他元素都赋值为0，若量化精度为B，则：

1.2 数字预编码

在混合预编码中，数字预编码部分一般使用线性预编码。实际上，数字预编码就是用于消除用户干扰的传统的预编码。由文献[9]可知，线性预编码达到的性能与非线性预编码相似，且复杂度较低。但是，随着系统收发两端天线数量的增多，线性预编码的运算复杂度不断增大，制约了其发展。为了解决复杂度的问题，引入了格基规约技术。格基规约算法可以提高等价信道矩阵的正交特性[10]。近来，格基规约（Lattice Reduction，LR）技术不断发展，在MIMO 系统中的应用逐步扩展。在多用户MIMO系统中，基于格基规约技术的低复杂度预编码受到了很多关注。格基规约线性预编码算法[11-12]可以看作是基于格基规约线性检测算法在发送端的对偶处理。根据不同的准则，它可以分为两种形式：一种是基于格基规约技术的迫零（Lattice Reduction-Zero Force，LR-ZF）预编码算法；另一种是基于格基规约技术的最小均方误差（Lattice Reduction-Minimum Mean Square Error，LR-MMSE）预编码算法[11-12]。本文主要研究基于格基规约技术的破零预编码算法在自适应混合预编码中的应用。

2 格基规约技术在线性预编码中的应用

2.1 格基规约技术

对信道矩阵H应用格基规约算法，先对信道矩阵HT进行QR 分解：

式中，Q是N×K正交矩阵，R是K×K上三角矩阵。根据CLLL 复格基规约算法[7]对HT进行格基规约，得到正交性更好的约减基矩阵为上三角矩阵需满足以下两个条件：

式中，表示上三角矩阵中位于第i行第k列的元素，约减参数T通常取3/4。

CLLL 格基规约算法生成的单位模矩阵T中的元素均为复整数，初始基矩阵HT与得到的约减基矩阵的关系为：

假设发送端可以获得全部信道状态信息，对于混合预编码中的数字预编码采用ZF 预编码，将格基规约技术与ZF 预编码结合，构成基于格基规约技术的ZF 预编码算法。此算法是对信道矩阵H的转置进行格基规约[13]，即用正交性更好地约减信道矩阵来进行预编码：

由于是等效信道，z=FX是等效发送信号，使用单位模矩阵T来恢复原始发送信号后得到s=Tz。

2.2 格基规约在混合预编码中的应用

接收信号可以表示为：

式中，H∈CK×N是信道矩阵；F=[f1f2…fk]∈CN×K为模拟预编码矩阵；W是数字预编码；s为发送信号，经过空时编码后形成两个支流s1和s2；N为加性高斯白噪声。若使用格基规约迫零预编码，有：

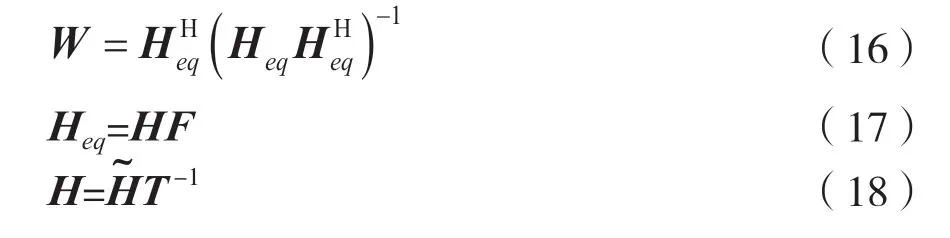
3 仿真结果

图2 是基于格基规约技术的线性预编码算法CLLL-ZF 和传统的线性预编码算法ZF 的方案误码率随信噪比（Signal to Noise Ratio，SNR）变化的对比仿真。发送端有6 根天线，接收端有3 个单天线用户，信道为平坦瑞丽衰落信道，噪声是加性高斯白噪声，调制方式为QPSK。由图2 可知，误码率为10-3时，CLLL-ZF 方案与ZF 方案相比，约有3 dB 的增益，这是因为格基规约与迫零预编码结合时提高了信道的正交性，从而提高了线性预编码的性能。

图2 CLLL-ZF 和ZF 的误码性能对比

图3 是大规模MIMO 下基于格基规约的迫零（CLLL-ZF）混合预编码和数字预编码只有迫零（ZF）预编码的混合预编码两种方案误码性能对比。发送端配备128 根天线，接收端有4 个单天线用户，取QPSK 调制，假设信道是平坦瑞丽衰落信道。由图3 可知，误码率为10-2时，CLLL-ZF 的混合预编码与ZF 混合预编码相比，约有3 dB 的增益，这是因为在数字预编码中，格基规约与迫零预编码结合时提高了信道的正交性，从而提高了系统的性能。

图3 两种方案误码性能对比

4 结语

本文研究了格基规约技术在混合预编码中的应用，分别分析了传统的迫零数字预编码和基于格基规约的迫零预编码两种不同的方案，并将基于格基规约的迫零预编码方案运用在大规模MIMO 中，使系统能够降低系统复杂度和提高系统性能。