基于极化转化超表面的雷达散射截面减缩*

商婷婷，赵 敏，赵建平，徐 娟

（曲阜师范大学，山东 曲阜 273165）

0 引言

雷达散射截面（Radar Cross Section，RCS）的缩减，可以通过将后向散射波漫反射重新定向到不同的方向来获得。2007 年，Paquay 等人提出了一种新的方法，使用以棋盘状形式形成的完美电导体（Perfect Electric Conductor，PEC）和人工磁导体（Artificial Magnetic Conductor，AMC）单元的组合来减少RCS[1]。该方法中，由于AMC 和PEC 单元的相位抵消特性，有效降低了后向散射能量被。为了提高PEC 单元的带宽，将其中的一个单元用另一个AMC 单元取代。具有不同谐振频率的两个AMC单元的组合导致在宽带中产生180°相位差，从而增加带宽，降低RCS[2-3]。虽然以上方法可以有效使目标RCS 降低并提高带宽，但结构更加复杂。。

目前，缩减RCS 的有效技术是利用电磁波的极化特性，通过交叉极化转换产生相位差，实现散射分量相消[4]。本文设计了一款高性能极化转化超表面单元，通过单元与镜像单元实现交叉极化分量相消，利用不同尺寸的极化转化单元实现共极化分量相消，且采用交叉式排列更有效地缩减了RCS。

1 极化转化超表面的基本理论

将x、y直角坐标系沿逆时针方向旋转135°得到u、v直角坐标系，极化转化超表面的工作原理将以u、v直角坐标系为例进行阐明。假设以沿-z方向传播的x极化入射波为例，当入射波垂直入射到超表面单元的结构层时，入射波电场将分别沿u、v轴作正交分解。入射电场为：

入射电磁波经极化转化超表面反射后，反射电场为：

引入反射系数，则反射电场为：

在不考虑入射波被吸收或者被损耗的情况下，由于金属地板的全反射特性，可近似认为反射系数的绝对值等于1。由于各向异性作用，当超表面单元结构发生磁谐振时，材料的磁导率μ将趋于无穷大，介电常数ε基本保持不变，则材料表面的阻抗将无穷大，超表面单元结构可以等效为高阻抗表面，反射相位为0°。但是，这种情况存在一定的理想性，材料的磁导率并不会变化很大。由于金属地板的全反射特性，因此反射相位为180°，之间的相位差也就是180°[6-7]。当电磁波分别以u极化和v极化方式入射时，反射电场的方向将沿y轴方向，实现了x极化入射波转为y 极化反射波。

2 单元设计

基于上述极化转化超表面的基本理论，提出了一款极化转化超表面单元如图1 所示。单元结构包括3 层，由下到上依次为金属地板、介质基板和结构层，具体参数如表1 所示。介质板采用Rogers 5880 的基板，相对介电常数为2.2，损耗正切角为0.000 9。单元通过改变角度theta的大小，得到两种极化转化超表面单元（单元1、单元2）。将这两种单元分别进行镜像操作，可以得到对应的镜像单元。图2 为极化转化单元的镜像单元。

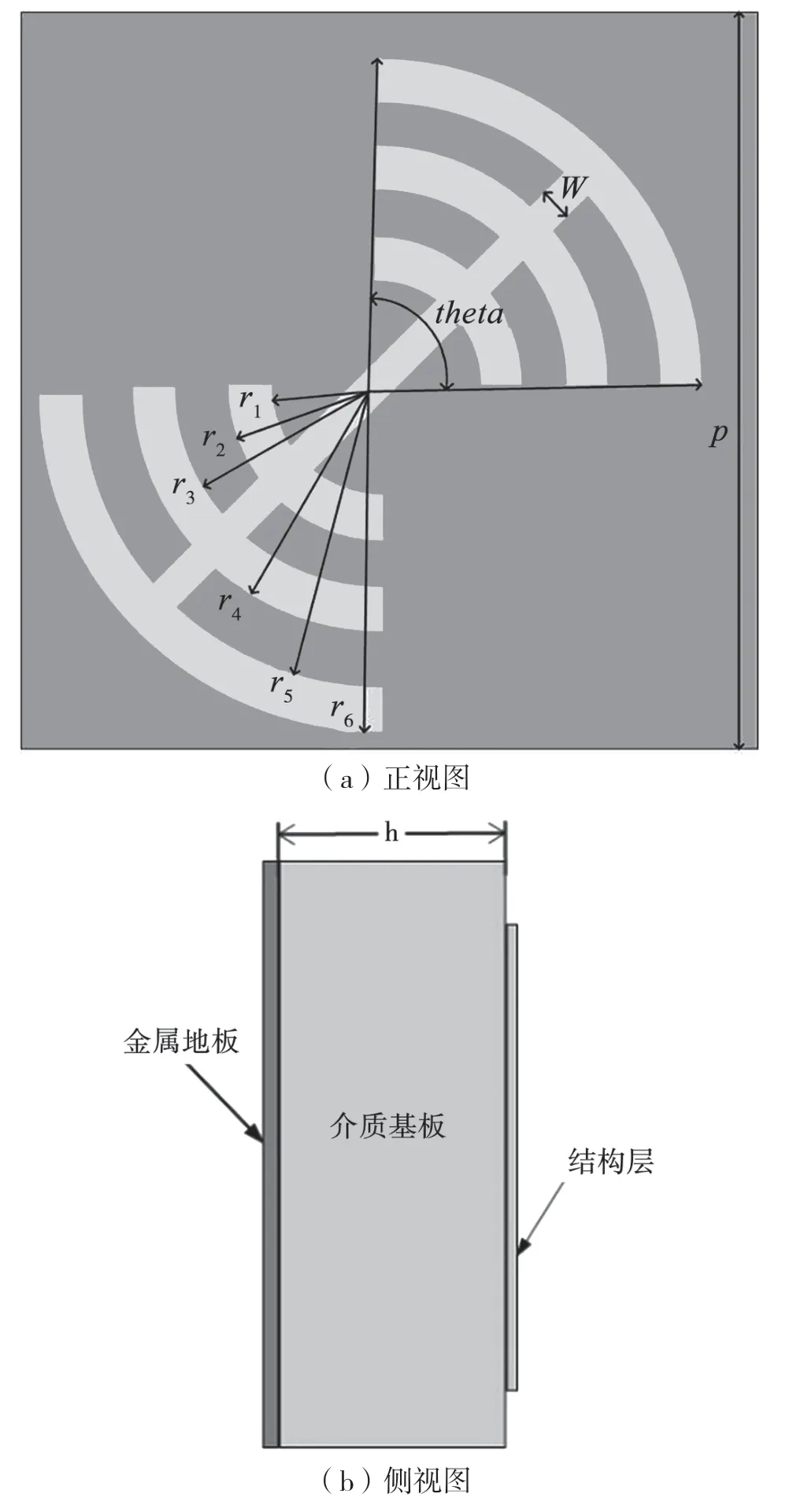
图1 极化转化超表面单元

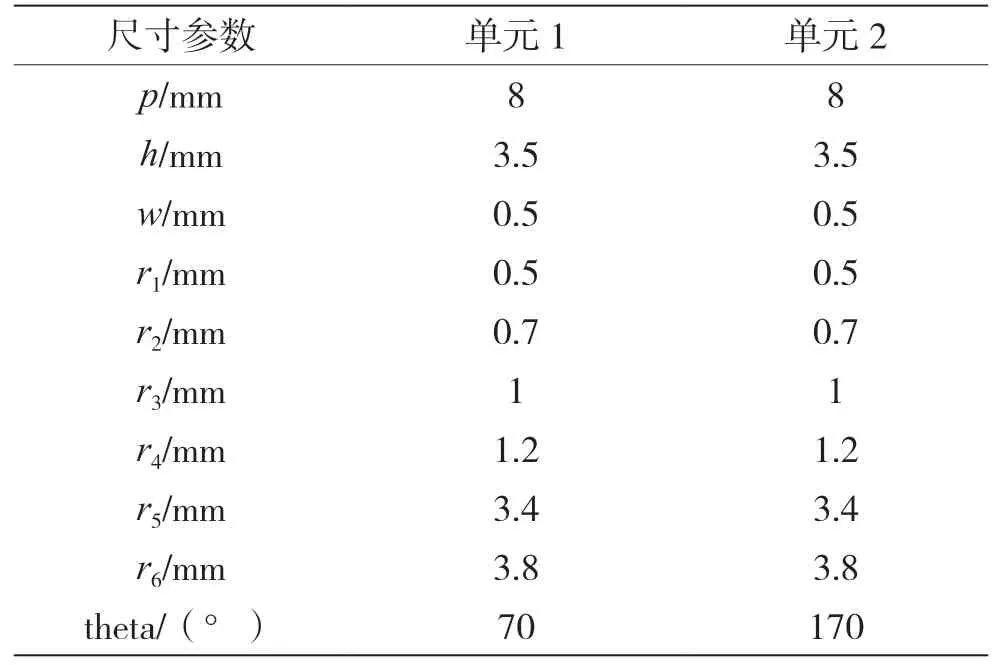
表1 极化转化超表面单元的具体参数

图2 极化转化超表面镜像单元

为了分析极化转化单元的散射特性，通过商业仿真软件HFSS13 对单元进行仿真与优化。以theta=70°的极化转化单元1 为例，当垂直入射的平面波p沿x方向极化时，根据极化转换的原理，散射波会被转换到y方向极化。定义极化转换率（Polarization Conversion Rate，PCR）为[8]：

由于基本单元和其镜像单元具有相同的极化转化率，因此图3 给出了极化转化超表面单元1 和单元2 的极化转化率曲线。

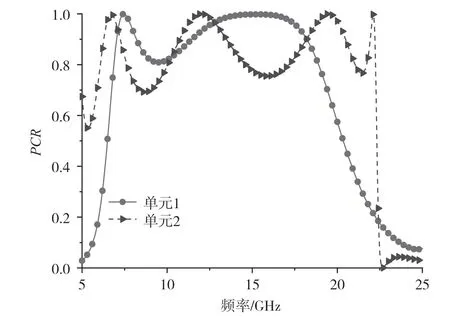
图3 极化转化超表面单元结构的极化转化率

图4 给出了基本单元和其镜像单元的交叉极化散射分量相位之间的关系。单元1 和单元2 分别和它们的镜像单元在整个频段内交叉极化散射分量相位差始终为180°，实现交叉极化散射分量相消。

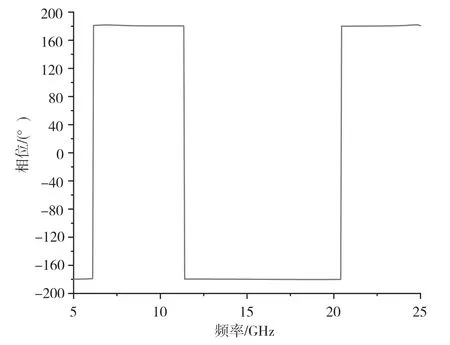
图4 交叉极化散射分量相位差

图5 则给出了极化转化超表面单元1 和单元2之间的共极化反射相位之间的关系。在12.5～19.5 GHz 范围内，单元之间的共极化反射相位差保持在180°，实现单元之间共极化散射分量反向相消。

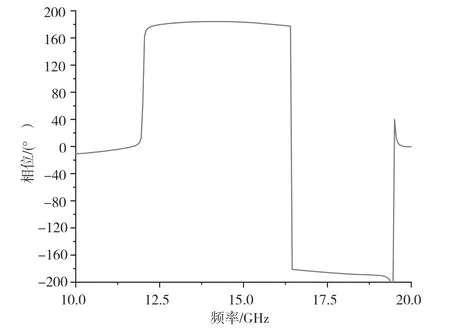
图5 共极化反射相位差

3 超表面阵列排布

3.1 棋盘式排列

基于上述极化转化单元的特性，将两种尺寸的单元构成了传统的棋盘式排列。图6 采用了12×12的极化转化单元来构造超表面阵列。

图6 极化转化超表面棋盘式排列结构

采用等大的普通金属板与棋盘式排列进行对比RCS 缩减，如图7 所示。在5～25 GHz 频段内，棋盘式排列的RCS 值要明显低于普通金属板的RCS 值。

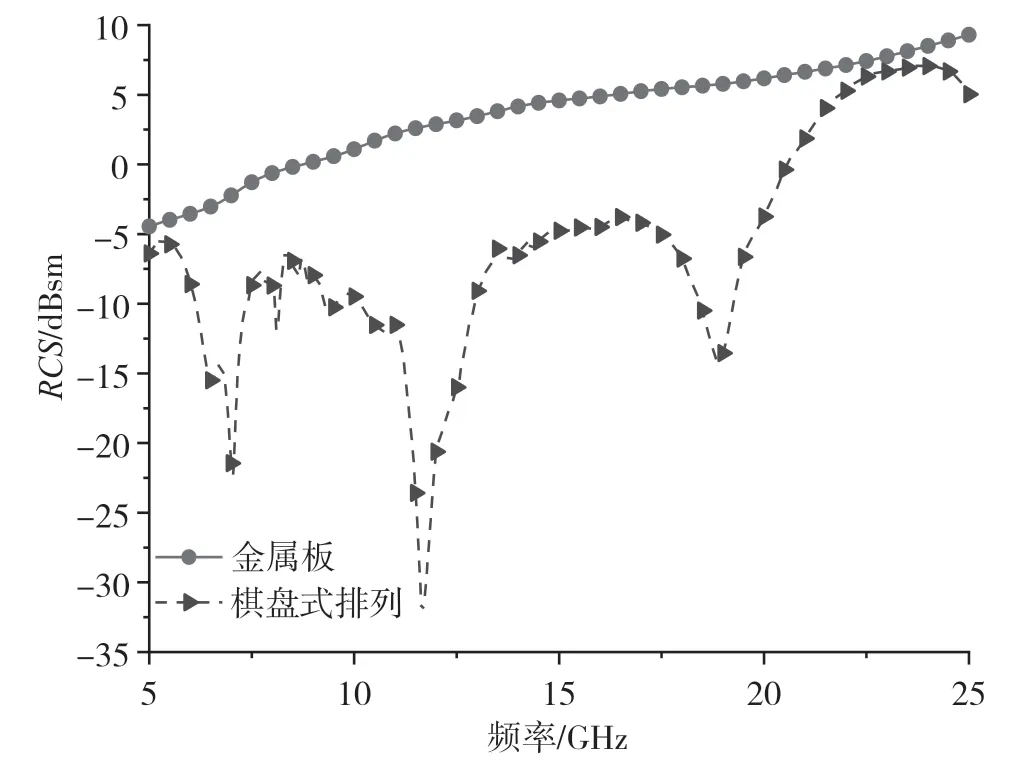
图7 在5～25 GHz 频段内的RCS 特性

在谐振频率15 GHz、phi=0°处，图8 为棋盘式排列超表面将垂直方向散射波束分为了两束波束。

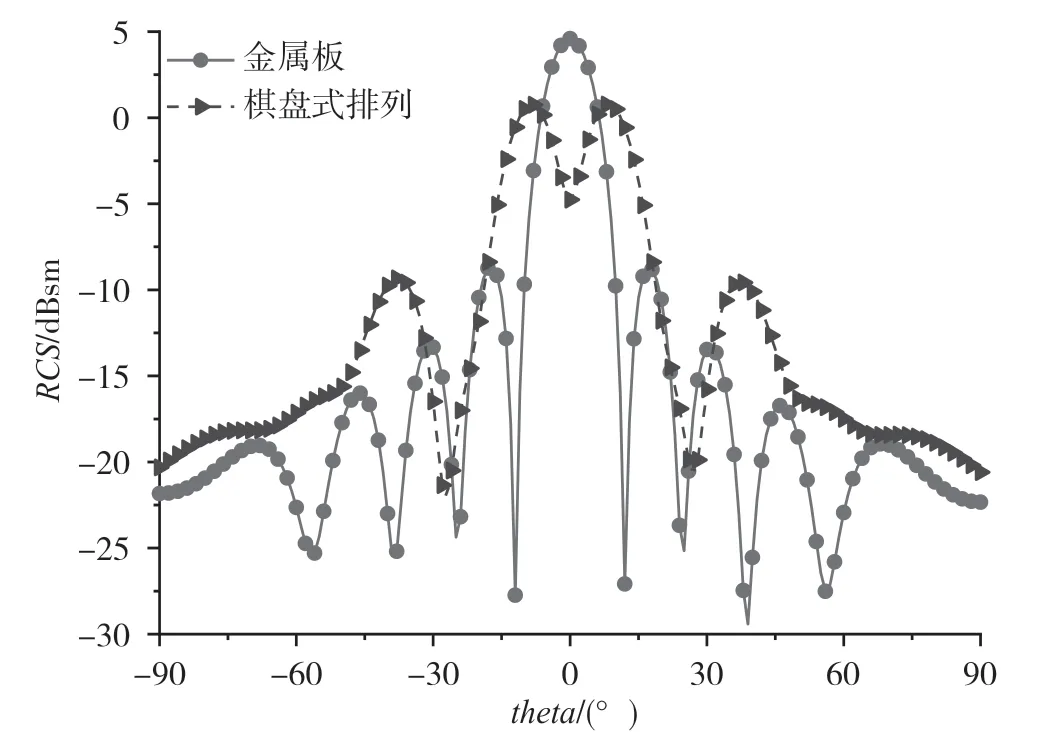
图8 在频率为15 GHz、phi=0°处RCS 特性

为了更直观地观察超表面的散射能量分布情况，图9 给出了金属板和棋盘式排列在谐振频率15 GHz处的3D 散射特性图。可以看到，RCS 在垂直方向有显著减缩。同时，伴随着两束倾斜波束的出现，垂直方向的RCS 缩减是基于能量重新辐射到其他方向。

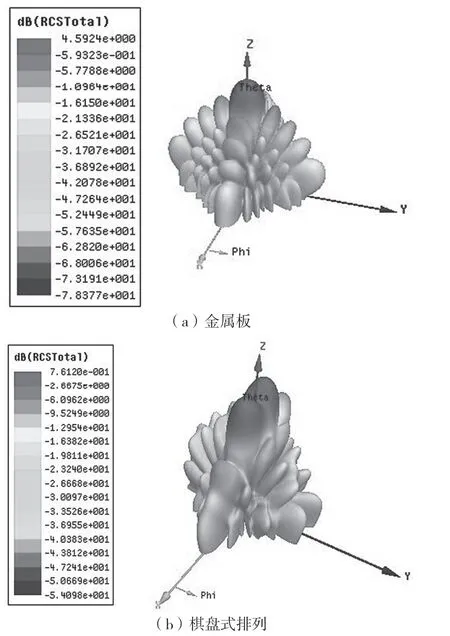
图9 入射波垂直照射下，在15 GHz 处的3-D 散射场

3.2 交叉式排列

通过对传统的棋盘式排列的超表面仿真分析，发现每个单元的排列数量会影响RCS 的缩减情况。将原来每种单元6×6 排列减少到4×4，为了能与传统的棋盘式排列的超表面进行对比，保持口径大小不变，单元的排列按照上述分析的极化转化单元特性进行分布排列。图10 是进行重新排列后的超表面交叉式排列结构。

采用同口径的棋盘式排列与交叉式排列进行对比RCS 缩减，如图11 所示。在5～25 GHz 频段内，两种排列方式的RCS 缩减情况基本保持一致。如图12 所示，在谐振频率15 GHz、phi=0°处，交叉式排列超表面的RCS 值要明显低于棋盘式排列超表面的RCS 值，大约降低了5 dB。为了更直观地观察交叉式排列超表面的散射能量分布和RCS 缩减的情况，图13 给出了交叉式排列和棋盘式排列在频率为15 GHz 处的3D 散射特性图。从图13 可以看到，RCS 在垂直方向有显著减缩，同时伴随着多个波束的出现。也就是说，垂直方向附近的RCS 值缩减是基于能量重新辐射到其他方向。

图10 极化转化超表面交叉式排列结构

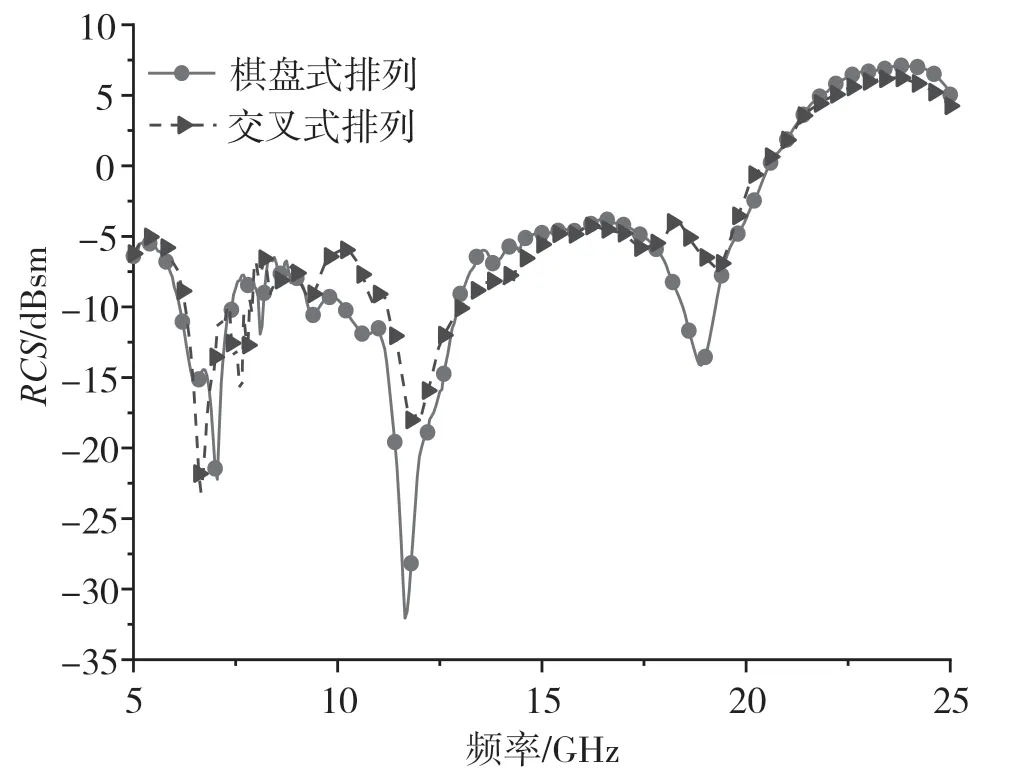
图11 在5～25 GHz 频段内的RCS 特性

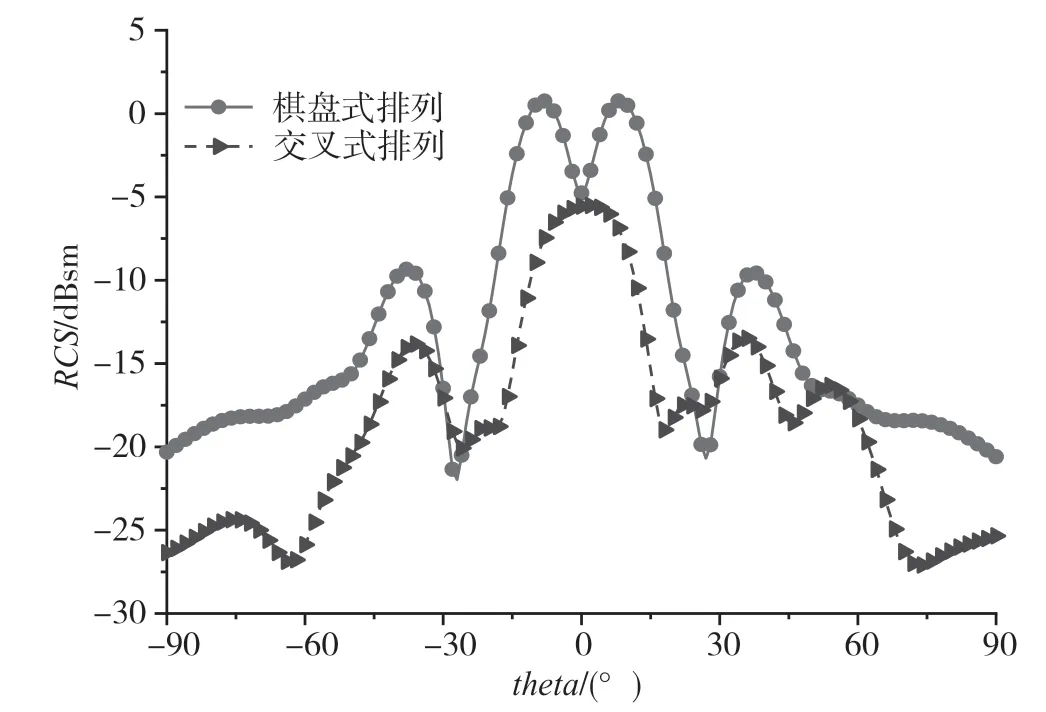
图12 在频率为15 GHz 处RCS 特性（phi=0°）

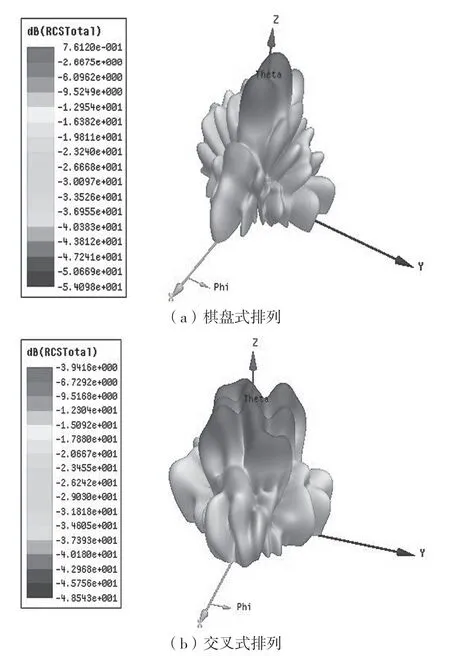
图13 入射波垂直照射下，在15 GHz 处的3-D 散射场

4 结语

本文设计了一款极化转化超表面单元。通过极化转化单元与其镜像单元交叉极化相位差为180°，实现了交叉极化分量相消；利用不同尺寸的极化转化单元存在共极化相位差为180°，实现了共极化分量相消。仿真结果表明，将极化转化单元和其镜像单元采用交叉式排列，后向散射波可被分为多个波束，也就是将垂直方向的能量尽可能重新辐射到其他方向，实现后向RCS 的缩减。