基于改进LLL规约的MIMO系统解码算法*
2017-01-11韩志勇王泽宇
韩志勇 王泽宇
(91919部队 黄冈 438000)
基于改进LLL规约的MIMO系统解码算法*
韩志勇 王泽宇
(91919部队 黄冈 438000)
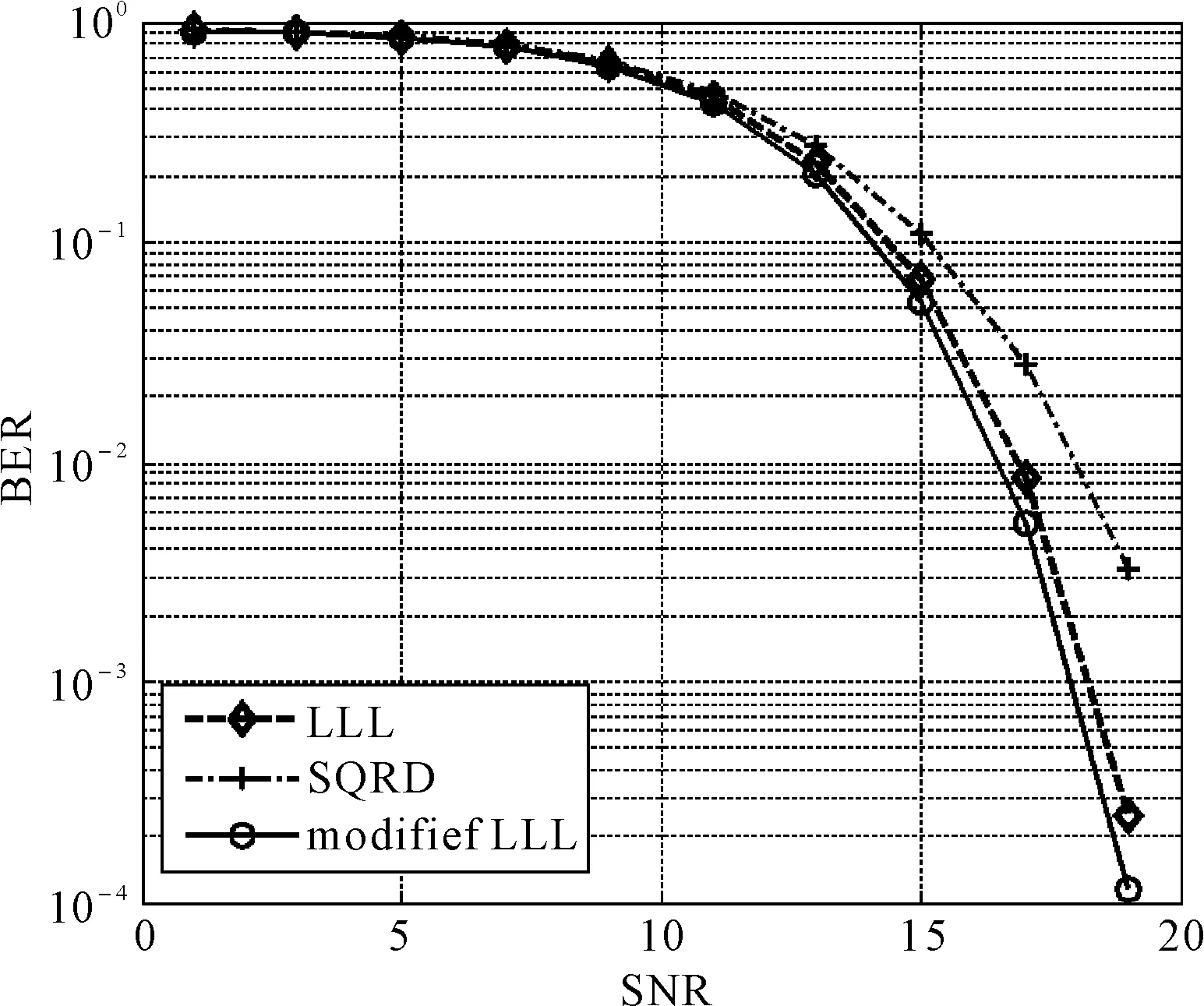
LLL算法是一种经典的格基规约算法,它广泛应用于MIMO通信系统的线性接收机中。LLL算法依赖于Gram-Schmidt正交化算法,这种算法按照增益矩阵中向量的初始顺序产生正交基。论文提出一种排序Gram-Schmidt正交化算法,这种算法可以产生更短的正交基。然后在LLL算法中,用排序Gram-Schmidt正交化算法代替原正交化,以改进规约算法的性能。在仿真实验中,比较了论文提出的改进LLL算法、LLL算法和排序QR分解算法的解码性能。结果显示本文提出的方法误码率(BER)最低。
多输入多输出; 格基规约; LLL; Gram-Schmidt正交化
(No. 91919 Troops of PLA, Huanggang 438000)
Class Number TP301.6
1 引言
MIMO技术能在不提高发射功率或者增加通信带宽的情况下,提高数据的传输速率,增强无线信道的可靠性,是一种非常实用有效的通信技术。虽然MIMO技术让高吞吐量的数据通信成为可能,但是也面临如何在接收机端可靠解码数据的挑战。幸运的是,以LLL算法为代表的格基规约技术的应用,大大增加了数据解码的可靠性。
在数学领域,对格基规约的研究可以追溯到18/19世纪。Lagrange,Hermite,Korkine与Zolotarev以及Minkowski分别在不同条件下提出了规约基的算法[1~4]。但是这些算法大多停留在纯理论领域,很难实际应用。重大突破来自于Lenstra,Lenstra和Lov’asz一起提出了LLL规约,并给出了具体的实现算法[5]。由于LLL规约能够在多项式时间内实现,因此得到了各行各业最广泛的应用:从计算机科学到密码学[6~7],从卫星导航精密定位到MIMO系统通信[8~9],都可以看到LLL算法的身影。
另一方面,诸如排序QR分解为代表的排序分解算法,也可以取得很高的解码可靠性[9]。本文通过把排序QR分解中的排序引入LLL算法,提出了一种新的LLL改进算法,并把新算法应用到MIMO系统解码中。仿真实验表明,本文提出的改进LLL算法性能优于LLL算法和排序QR分解算法。
2 MIMO系统格基规约
考虑一个由m个发信机和n个接收机(m≥n)组成的m×n维MIMO通信系统。发送信号向量x和接收信号向量y之间的关系可描述为
y=Gx+w
(1)
其中G=[g1,g2,…,gn]是一个m×n维的复矩阵,代表平缓衰弱瑞利信道中的增益矩阵;w是高斯分布的加性噪声,其元素互相独立。所谓“格”:l⊂m×n,是复数空间m×n的一个离散子集,它的元素全部由一组格基g1,g2,…,gn∈m×n通过整数系数的线性组合构成:
L(G)={∑xigi|xi∈}
(2)
一个格可以由无数组格基组成,其中一些格基具有非常优良的性能,这些格基被称作“规约的”。LLL规约算法就是把“非规约的”格基变换成“规约的”格基的算法,它包括三个部分:Gram-Schmidt正交化,长度规约和向量交换。
2.1 Gram-Schmidt正交化
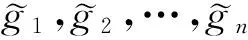
(3)
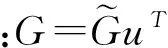
算法一 Gram-Schmidt正交化
输入:向量序列g1,g2,…,gn
2: fori=2:n
3: forj=1:i-1
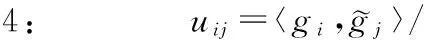
5: end for
7: end for
2.2 LLL算法
定义1 一个格基G={g1,g2,…,gn}∈n可以被称作是δ-LLL规约的,当且仅当以下两个条件同时满足:
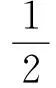
2) ∀1≤i 式中δ∈(1/4,1]是一个可调参数,为了达到算法性能和复杂度的平衡,通常取δ=3/4。上式中的第一个条件叫“长度规约”,它保证规约后向量之间的近似正交性。第二个条件叫“Lovász条件”,它保证规约基的长度不至于缩减太快。记“〔·〕”为取整符号,长度规约可步骤可描述为算法二。 算法二 长度规约 输入: 格基G={g1,…,gn}∈▯n,Gram-Schmidt参数矩阵u 输出: 长度规约基G 1: fori=2:n 2: forj=i-1:n 4:gi=gi-〔uij〕gj,uij=uij-〔uij〕 5: forl=1:j-1 6:uil=uil-〔uij〕uil 7: end for 8: end if 9: end for 10: end for 算法二用gi之前的向量g1,g2,…,gi-1对gi进行长度规约。所造成的结果是越往前面的向量,规约越不充分。为了对所有向量充分进行规约,LLL算法一边进行长度规约一边进行向量位置交换。如果“Lovász条件”在向量gi处不满足,那么gi和gi+1交换,算法后退至gi-1;否则执行长度规约后,算法前进至gi+1继续判断“Lovász条件”。LLL算法的执行步骤可描述为算法三。 算法三 LLL算法 输入: 格基G={g1,…,gn}∈n,参数δ 输出: 规约基G 2:i=2 3: whilei≤n 4: 对gi执行长度规约 6: 交换gi和gi+1,更新Gram-Schmidt正交基 7:i=max(i-1,2) 9: else 10:i=i+1 11: end if 12: end while 从上节叙述可知,LLL算法只对相邻近的向量进行交换。Chang (2005)在GNSS定位领域的研究显示:在规约前对向量进行统一排序,能进一步提高规约性能[10]。著名的SQRD算法就是一种这样的排序算法(Wübben等2000)[9]。在这一节中,我们把SQRD算法引入Gram-Schmidt正交化过程,提出排序Gram-Schmidt正交化算法。 算法四 排序Gram-Schmidt正交化 输入:向量序列g1,g2,…,gn 1:gk=min:1≤i≤n‖gi‖ 3: forl=2:n 4: fori=l:n 5: forj=1:i-1 7: end for 9: end for 12: end for 用排序Gram-Schmidt正交化算法对LLL算法进行改进,就是把LLL算法步骤一中的Gram-Schmidt正交化替换成排序Gram-Schmidt正交化算法,然后再执行标准的LLL规约过程。因为排序Gram-Schmidt正交化算法每一步得到的正交化向量长度都不长于原Gram-Schmidt正交化。在更短的正交基下再进行LLL规约可以得到更好的规约基,同时缩短规约时间。 由于格基规约算法在接收机端解码的巨大作用,导致了以LLL算法为代表的规约算法在实时MIMO通信中的巨大应用。本节通过仿真一个瑞利衰落信道下的MIMO接收机解码算法。分别比较应用SQRD、LLL算法和本文提出的改进LLL算法的MIMO系统的比特误码率(BER)。 实验中设置在发送方和接受方的天线数量均为4,数据调制方式基于64-QAM,数据解码方案设置为迫零检测(ZF)。在上述实验方案下,三种算法的解码比特误码率如图1所示。结果显示,随着信噪比(SNR)的提高,三种算法的BER均大幅下降。其中基于改进LLL算法的解码有最低的BER,略低于原LLL算法,远低于SQRD算法。例如图中显示,当BER小于10-2时,基于改进的LLL算法的解码可以获得2dB的增益。这说明了改进LLL算法优于其它两种算法,实验结果符合本文预期。 图1 三种算法在64-QAM调制下4×4 MIMO系统中的BER性能表现 为了加强MIMO系统解码性能,本文提出了一种改进的LLL规约算法。在改进LLL算法中,引入了经典的SQRD排序改进Gram-Schmidt正交化算法,使得Gram-Schmidt正交化能够获得更短的正交基。基于更短正交基的LLL规约可以获得更好的规约性能。基于一组64-QAM调制下4×4 MIMO系统接收机解码仿真实验,比较了SQRD、LLL算法和改进LLL算法的性能,结果表明本文提出的改进LLL算法由于其它两种算法。 [1] Lagrange L. Recherches d’arithm`etique, Nouv. M`em[M]. Berlin: Acad,1773. [2] Hermite C. Jacobi sur diff’erents objets de la th’eorie des nombres[J]. J Reine Angew Math,1850,40:279-290. [3] Korkine A, Zolotarev G. Sur les formes quadratiques[J]. Math Ann,1873,6(3):366-389. [4] Minkowski H. Geometrie der Zahlen[M].Stuttgart:Teubner-Verlag,1896. [5] Lenstra AK,Lenstra HW Jr,Lov′asz L.Factoring polynomials with rational coefficients[J].Math Ann,1982,261:515-534. [6] Papachristoudis DG,Halkidis ST,Stephanides G.An experimental comparison of some LLL-type lattice basis reduction algorithms[J].Int J Appl Comput Math,2015,1(3):327-342. [7] Fontein F,Schneider M,Wagner U.PotLLL:a polynomial time version of LLL with deep insertions[J].Des Codes Cryptogr,2014,73:355-368. [8] Jazaeri S,Amiri-Simkooei A,Sharifi MA.On lattice reduction algorithms for solving weighted integer least squares problems:comparative study[J].GPS Solut,2014,18:105-114. [9] Wübben D,Böhnke R,Rinas J,et al.Efficient Algorithm for Decoding Layered Space-Time Codes[J].Electronics Letters,2000,37:1348-1350. [10] Chang X,Yang X,Zhou T.MLAMBDA:A Modified LAMBDA Method for Integer Least-Squares Estimation[J].J Geod,2005,79:552-565. A Modified LLL Reduction Aided MIMO System Decoding Method HAN Zhiyong WANG Zeyu The classical lattice reduction algorithm, known as the LLL, is widely applied in the linear receivers of the multiple-input-multiple-output (MIMO) system. The LLL depends on the Gram-Schmidt orthgonalization (GSO) which generates the orthogonal basis by the original order. In this contribution, a sorted GSO strategy is proposed in order to obtain shorter orthogonal basis of the lattice. Then the LLL algorithm is modified by replacing the standard GSO with the sorted one. In the simulation study, the modified LLL, classical LLL and the SQRD are compared. The result has revealed that the proposed algorithm is superior to the other two in the term of the bit-error-rate (BER) performances. MIMO, lattice reduction, LLL, GSO 2016年6月6日, 2016年7月17日 国家自然科学基金项目(编号:41504029)资助。 韩志勇,男,硕士,工程师,研究方向:移动通信,对潜通信。王泽宇,男,助理工程师,研究方向:短波通信。 TP301.6 10.3969/j.issn.1672-9730.2016.12.024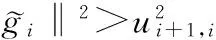
3 基于排序Gram-Schmidt正交化的LLL改进算法
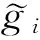
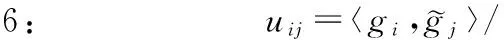
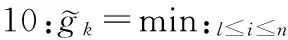
4 仿真实验
5 结语
