衰落信道基于卡尔曼滤波的信噪比估计*

刘世洪，夏洪君，蒋元兵，颜浩洋，穆 刚

（重庆金美通信有限责任公司，重庆 400030）

0 引言

无线通信场景中，由于复杂的电磁环境及移动通信双方之间的相对运动，使无线信道存在着严重的多径衰落及多普勒效应[1]。为均衡多径衰落或多普勒效应的影响，移动通信双方多采用协同降速、信道切换、分集接收、联合解码等策略，来克服信道影响，进而提高传输信息的可靠性。因此，如何获取无线通信中的信道特性，并选用合理的参数（如信噪比、多径、时延、衰落等）来评估信道及指导通信策略，成为无线通信的一个重要研究方向。

信噪比作为信道传输的关键参数，用于衡量通信信号质量，即经过衰落特性后的信号能量与本地噪声能量之比。在无线通信双方，需要根据信噪比自适应协商合理的传输速率及带宽等通信参数，同时在解调处理中也需要利用信噪比来获得信道均衡、迭代译码等步骤中的较优参数。通常，信噪比估计算法根据是否利用同步头辅助分为两种：基于非同步头辅助（Non-Preamble Aided，NPA）与同步头辅助（Preamble-Aided，PA）算法[2]。常用的NPA 算法如二阶/四阶矩估计算法[3]，多用于PSK、QAM 类信号，主要对接收信号进行二阶矩或四阶矩处理，将信号与噪声分离，从而获取信噪比，但在衰落信道条件下估计性能较差，并且存在计算复杂度高等问题，难以适应无线通信的实时传输。在PA 算法中，如基于最大似然估计的方法多利用同步头序列构建似然函数来完成信噪比估计[4]。

本文主要针对多径衰落信道条件下的PA 信噪比估计算法开展研究，提出一种基于卡尔曼滤波辅助的信噪比估计算法。首先利用卡尔曼滤波的方法对信道进行平滑。之后根据信道平滑方法的输出符号序列，以滑动时间窗的方式进行滑动，并计算其与已知辅助符号的均方根误差。当均方根误差趋于稳定时，选取合适的长度进行信噪比估计，从而为衰落信道条件下提升接收机信道质量评估精度、指导通信策略制定，提供技术支撑。

1 基本原理

1.1 无线通信数学模型

本文以无线通信中的串行体制为例进行调制及解调流程的描述，其中调制端原理框图如图1 所示，主要包括组帧、成形滤波、载波调制三个部分。

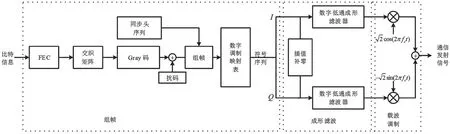
图1 调制端

①组帧：用于用户比特到数字调制符号序列的生成，输出IQ 符号序列，其中同步头序列可表示为p=[p0,p1,…,pL-1]，长度为L。

②成形滤波：用于适配IQ 符号与基带信号的采样速率，将IQ 符号序列转换为基带信号，此处采用平方根升余弦（Root Raised Cosine Filter，RRC）滤波器gT(t)进行成形滤波[5]，基带信号可表示为：

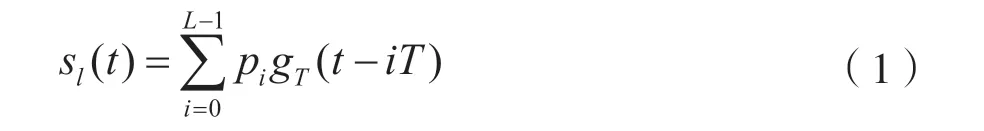
式中，T表示符号采样间隔。

③载波调制：用于将基带信号上边频转换为中频信号，对sl(t)进行载波调制：

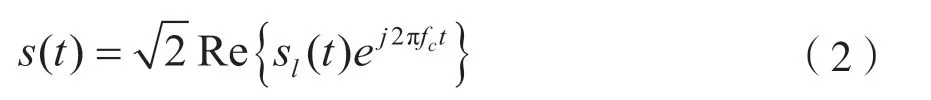
式中，Re{·}表示取实部运算，fc表示子载波频率，完成信号调制过程。

解调端的原理框图如图2 所示，其相对于调制端更为复杂，主要包括下变频、匹配滤波、信号同步、信道估计、解调译码等步骤。

首先对接收信号进行子载波下变频后得到：

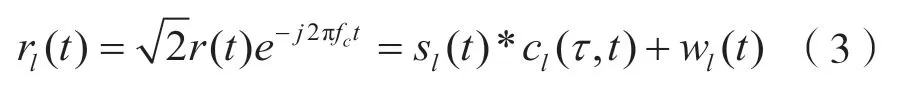
式中，c(τ,t)表示信道响应[6]，τ表示时延，wl(t)表示加性高斯白噪声，其功率谱密度为N0/2。然后对rl(t)进行匹配滤波，可得：

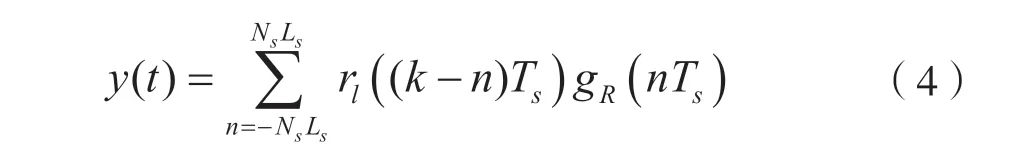
式中，Ts表示采样间隔，Ns=T/Ts为符号间隔与采样间隔之比，gR(t)表示匹配滤波器，其中，匹配滤波器与成形滤波器需要采用滚降系数相同的RRC滤波器，以保证符号间干扰最小。

之后，解调端利用y(t)进行同步（帧同步、载波同步、符号定时同步）、信道参数估计、判决译码等步骤，其中信噪比估计属于信道参数估计的范畴，也是本文研究的主要内容。

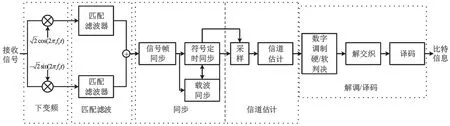
图2 解调端

1.2 PA 类算法

在无线通信系统中，信噪比估计在信号同步完成后，因此，接收符号序列y可表示为

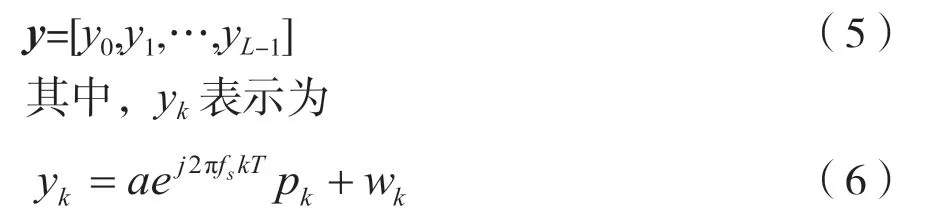
本节针对PA 算法中的基于最大似然（Maximum Likelihood，ML）估计的方法进行描述，ML 算法利用同步头符号序列p=[p0,p1,…,pL-1]与接收符号序列y=[y0,y1,…,yL-1]相关特性进行估计。

首先对p与y进行共轭相关计算得到：

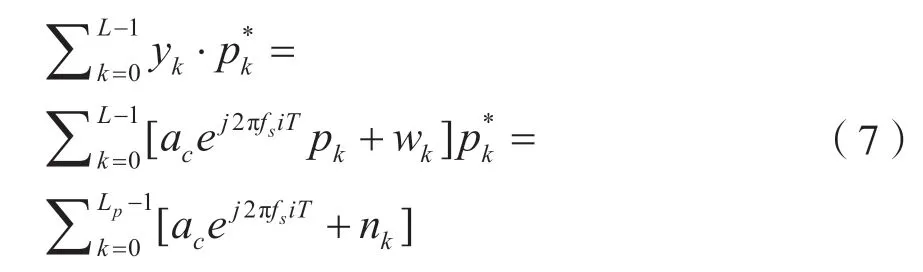
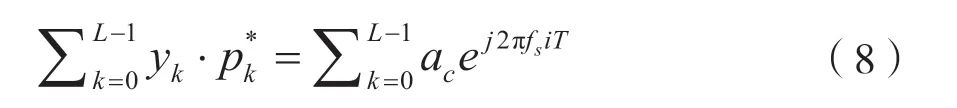
由于信道传播中幅度衰落a与频移f会直接导致接收符号能量衰减及星座图旋转[8]，因此在ML算法运算前需要先完成信道估计，消除a与f的影响，可得

即在yk´=pk+wk的条件下估计，最终估计信噪比为

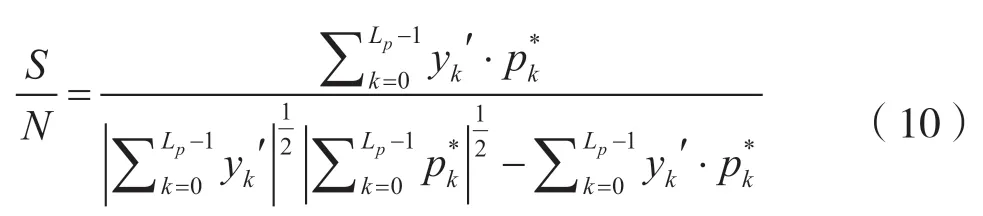
在无线通信中，同步头序列通常持续时间较短，与噪声序列独立，但存在一定的相关性（即相关值较小，不恒等于0），而ML 算法在信噪比估计之前需要优先完成幅度衰落、频移等信道参数的估计，在实际使用中存在一定的局限性。因此，本文基于PA 类算法进行改进，提出基于卡尔曼滤波辅助的信噪比估计算法。

2 基于卡尔曼滤波辅助的信噪比估计算法

基于卡尔曼滤波辅助的信噪比估计算法，用于衰落信道条件下的信噪比估计，首先利用卡尔曼滤波的方法平滑衰落信道影响，而后根据滤波器收敛特性选择信噪比估计的长度，最后利用无偏信噪比估计来完成估计。

2.1 基于卡尔曼滤波的信道平滑方法

本文采用基于卡尔曼滤波[9]的信道平滑方法，利用同步头序列p作为输入，采样符号序列y作为参考信号，其中，滤波器hn的抽头长度为K1+K2+1，K1与K2的取值由信道脉冲响应的最大时延来确定，信道估计器的框架如图3 所示。

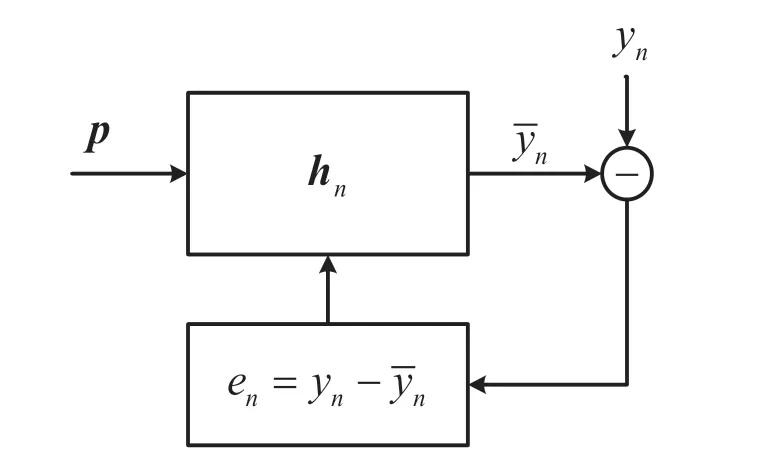
图3 基于卡尔曼滤波的信道平滑方法

当前输入符号序列可表示为yn=[yn+K1,…,yn,…,yn-K2]T，经过hn滤波器后，输出

式（11）中，hn=[hK1,…,h0,…,h-K2]T。此时，和参考信号之间的误差为

由于无线信道的参数是变化的，所以滤波器系数也必须要同步跟踪信道的变化，而RLS 算法[10]具有收敛速度快、适于跟踪快速变化的信道、不受信道特性影响的特点，此时RLS 算法的代价函数[11]为

式（13）中，w表示加权因子，通常0＜w＜1。因此，将指数权重引入过去的数据，当信道特性是时变的时候，这样做是恰当的[12]。

对于ξ(n)相对于系数向量的最小化得到下列线性方程组：

式（14）中，RN(n)是接收符号序列的相关矩阵，可表示为

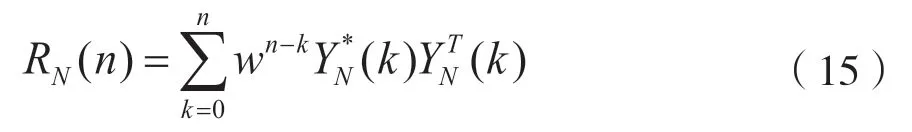
而DN(n)是互相关矩阵，定义为

为了避免对接收到的每一个新的信号分量求解式（17），即求解N个线性方程组，需要对RN(n)进行递推计算：

因此，基于卡尔曼滤波的信道平滑方法的步骤可归纳为：

①初始化PN(0)=δ-1IN，其中δ是一个正数常数；初始化BN(0)=[0,…,0,b0,0,…,0]T，其中b0=1；初始化YN(0)=[yk,…,y0,0,…,0]T；

③利用已知辅助符号xn直接计算误差e(n)=

④计算卡尔曼增益KN(n)；

⑤更新相关矩阵的逆运算QN(n)；

⑥更新滤波器系数BN(n)；

⑦重复②～⑥过程，直到完成所有符号的输出。

2.2 无偏信噪比估计算法

根据信道平滑方法的输出符号序列p=[p0,p1,…,pL-1]，以滑动时间窗的方式进行滑动，窗口长度可取K1+K2+1，并计算其与同步头符号的均方根误差，均方根误差计算如下：

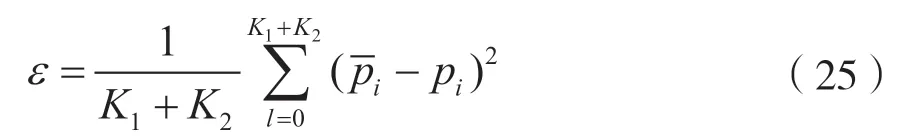
当均方根误差趋于稳定时，选取合适的长度Lp，计算信噪比。本方法首先利用复数相关等运算，估计噪声功率，再估计信号功率，从而得到信噪比。

首先，利用同步头序列与本地接收序列进行复数相关：

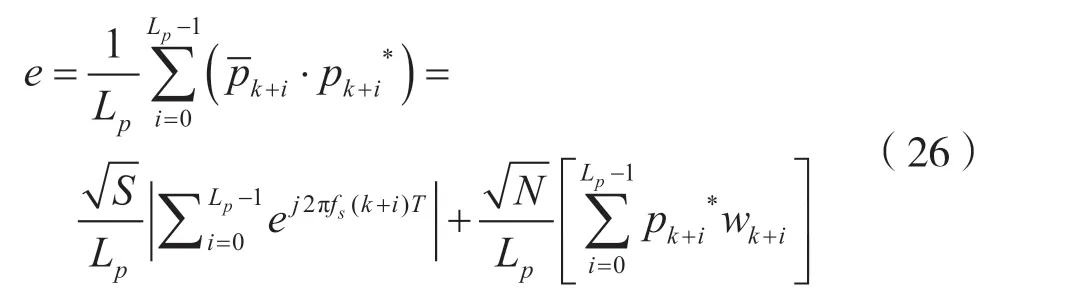
式中，wk表示高斯白噪声。e 的实部中包含了信号的幅度分量信息，对其取模、求平方可得

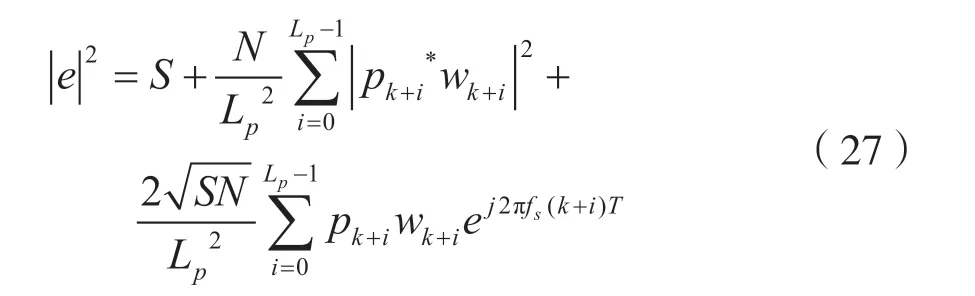
此时，对接收序列pk=[pk,pk+1,…,pk+Lp-1]求模，可得

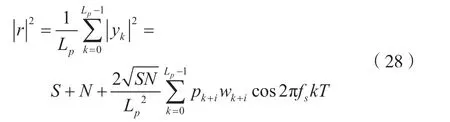
根据式（27）、式（28）可推导出

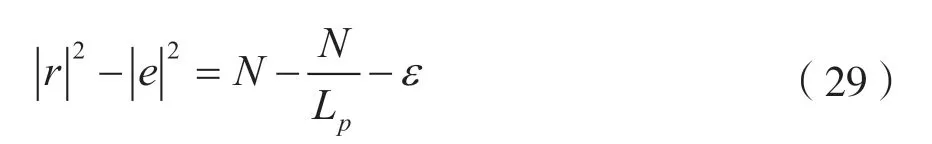
由于wk的均值为0，当随着Lp增大时，ε逐渐趋近于0。因此，获取噪声功率估计值，可表示为

同样，信号功率估计值可表示为：

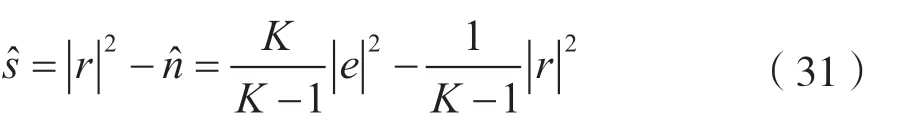
最终，本文算法的信噪比估计可表示为：

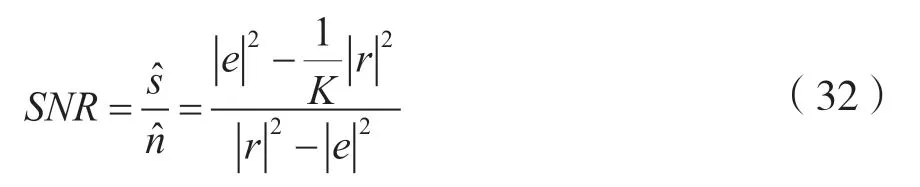
3 仿真与性能分析

为了验证衰落信道条件下信噪比估计算法的有效性，本节对上述信噪比估计算法进行仿真试验与性能分析。在仿真中，采用8PSK 调制的同步头序列作为已知信息，信道条件采用高斯信道、ITU好信道、ITU 中等信道及ITU 坏信道（不加入多普勒展宽），设定成形滤波器与匹配滤波器的滚降系数为0.4，其中，信噪比估计的均方误差（Mean Square Error，MSE）性能通过N=10000 次仿真试验得到，计算公式如下：

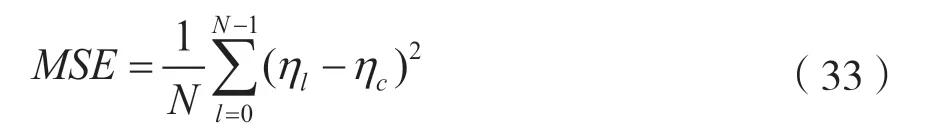
式中，ηc为设定的信噪比，ηl为第l次仿真试验的估计结果。

仿真1：设定同步头序列长度为L=512，选取滤波后滑动窗长度为Lp=128，信道条件为高斯信道、好信道（两条路径、0.5ms 延时）、中等信道（两条路径、1ms 延时）、坏信道（两条路径、2ms 延时），设定SNR 范围为-10～15 dB，对本文信噪比估计算法的进行均值及MSE 性能仿真，仿真结果如图4、图5 所示，其中实线表示经典信噪比估计算法、虚线表示本文算法。仿真结果表明：在高斯信道，两种方法性能相当；而在好信道、中等信道、坏信道条件下，经典算法特别是在SNR 大于0dB时无法获取较准确的信噪比，其估计值在0dB 之后趋于平滑，而本文算法可提供一定的估计性能，如SNR=10dB 时，可提供5～7dB 的信噪比估计均值，MSE 性能在5～77 左右。

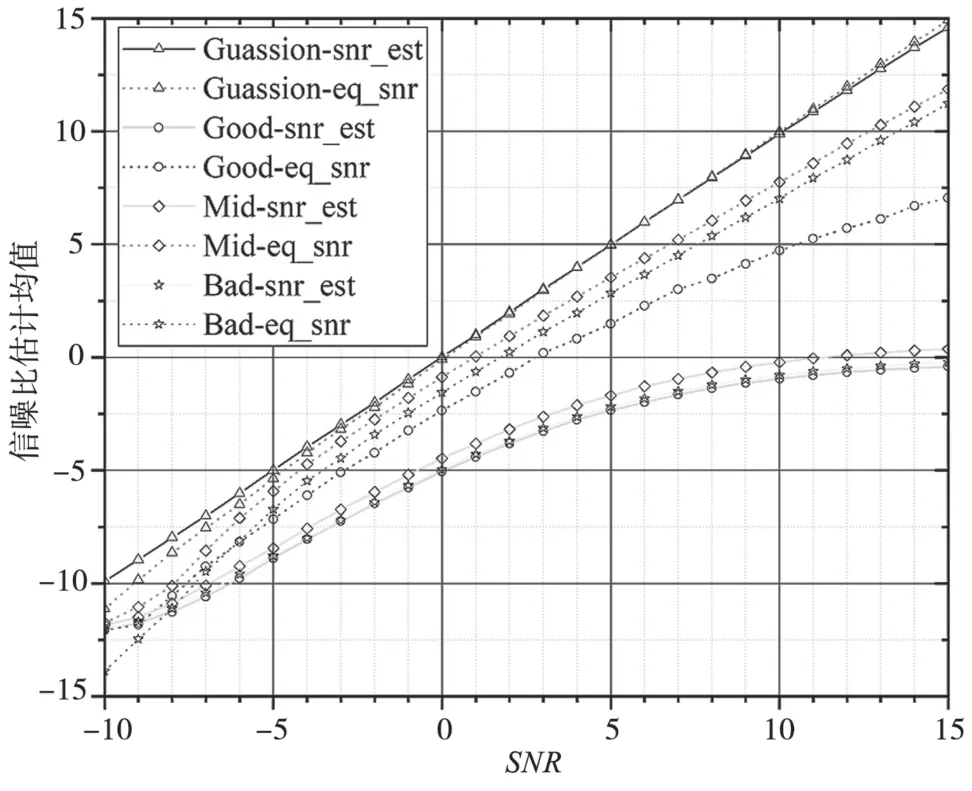
图4 SNR 估计均值曲线

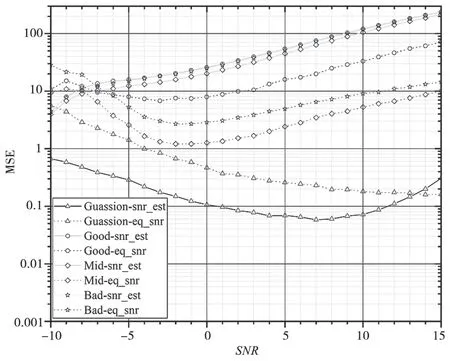
图5 SNR 估计均方差性能

仿真2：设定同步头序列长度为L=512，选取滤波后滑动窗长度为Lp=256，信道条件为高斯信道、好信道（两条路径、0.5ms 延时）、中等信道（两条路径、1ms 延时）、坏信道（两条路径、2ms 延时），设定SNR范围为-10～15 dB，对本文信噪比估计算法的进行均值及MSE 性能仿真，仿真结果如图6、图7 所示。仿真结果表明：在高斯信道，两种方法性能相当；而在好信道、中等信道、坏信道条件下，经典算法无法获取较准确的信噪比，其估计值在0dB 之后趋于平滑，而本文算法可提供一定的估计性能，如SNR=10dB 时，可提供5～8dB 的信噪比估计均值，MSE 性能在8～66 左右，性能略优于Lp=128。

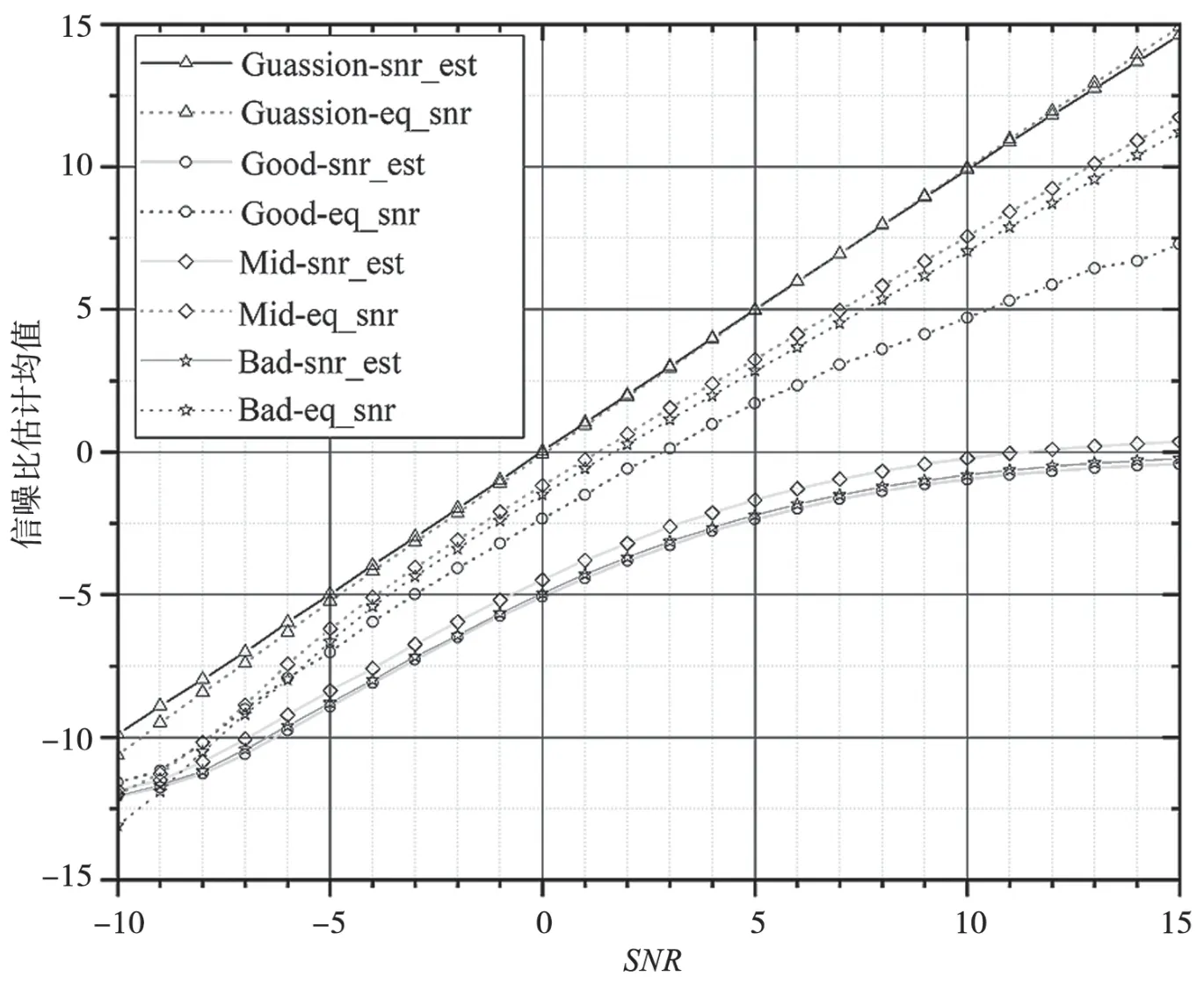
图6 SNR 估计均值曲线

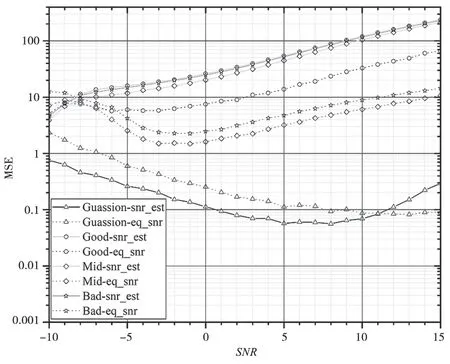
图7 SNR 估计均方差性能

4 结语

针对多径衰落信道条件的无线通信，本文提出一种基于卡尔曼滤波辅助的信噪比估计算法。首先利用卡尔曼滤波的方法对信道进行平滑，之后根据信道平滑方法的输出符号序列，以滑动时间窗的方式进行滑动，并计算其与已知辅助符号的均方根误差。当均方根误差趋于稳定时，选取合适的长度进行信噪比估计。通过在不同的信道条件下的仿真，并与经典信噪比估计算法等进行比较，发现本文算法不仅在高斯信道具有较高的估计精度，针对多径衰落信道较高斯信道估计性能存在2～5dB 衰减，具备一定的估计能力，因此本文算法可用于多径衰落信道条件下的信道质量评估，进而辅助指导通信策略的制定。