基于流固耦合的汽车双筒式减振器动态特性研究＊

2021-01-24邹琳秦傲李国嵩列煜俊徐劲力

汽车技术 2021年1期

邹琳秦傲李国嵩列煜俊徐劲力

（武汉理工大学，武汉 430070）

主题词：双筒式液压减振器阻尼特性复原行程流固耦合数值模拟

1 前言

减振器是悬架系统中最重要的组成部分之一，其性能对悬架系统整体性能起着至关重要的作用[1]。国内外学者对此进行了一系列研究。周长城[2]通过数学建模和理论计算分析了节流阀片受到压力时不同半径位置处的变形量。于振环[3]采用双向流固耦合法，将减振器活塞运动时阀片的变形反馈给流场，完整地分析了阀片变形前、后流场内的流动情况以及流场各处压力情况。马逸飞[4]运用AMESim 分析了覆盖节流阀片刚度、节流孔面积和充气压力等25个常规设计参数在多个典型运动工况下对示功特性的敏感性及其变化趋势。王伟[5]利用MATLAB 得到使悬架系统达到最佳阻尼匹配的减振器速度特性曲线。马天飞[6]运用AMESim建立了液压减振器的仿真模型，以优化设计软件Isight 集成AMESim，对模型进行了试验分析与优化设计，提高了设计效率，可用于指导减振器阀系参数的设计与性能预测。JanŁuczko[7]通过引入的非线性弹簧元件使液压减振器在大振幅激励的情况下免受损坏，提高了驾驶舒适性。Lalitkumar Maikulal Jugulkar[8]利用Fluent 研究了节流孔数量对汽车减振器在不同速度下的阻尼力和阻尼系数的影响。

本文利用ANSYS Fluent 软件中的用户自定义函数（User-Defined Function，UDF）描述补偿阀片的运动过程，对复原阻尼力进行完整数学分析，并对双筒阀片式液压减振器所建立的流固耦合模型进行计算流体动力学（Computational Fluid Dynamics，CFD）仿真分析。

2 双筒阀片充气式液压减振器数学建模

双筒充气式液压减振器是一种双作用式减振器，其基本工作原理是利用油液流经窄小孔隙产生的节流作用力和油液粘性产生的摩擦力来抵消车轮跳动传递至减振器的力并将动能转化为热能，以达到减振的作用，结构如图1所示。

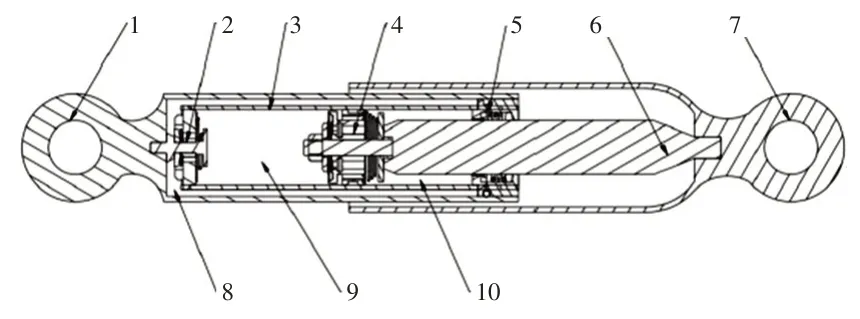
图1 双筒阀片式减振器结构示意

2.1 基本假设

为了简化数学模型，在数学建模中作出以下假设：

a.减振器内的油液为粘性不可压缩流体；

b.孔口处的流动是准稳态的；

c.内部腔室中的压强瞬时均匀化，即同一腔室内部压强处处相同[9]；

d.在一个行程中，内管液体温度不变；

e.减振器内部各处无弹性变形；

f.减振器在工作过程中不产生气泡；

g.活塞阀系与底座各处无缝隙。

根据以上假设和减振器的内部结构，建立等效物理模型，规定活塞杆向上运动为正方向，如图2所示。

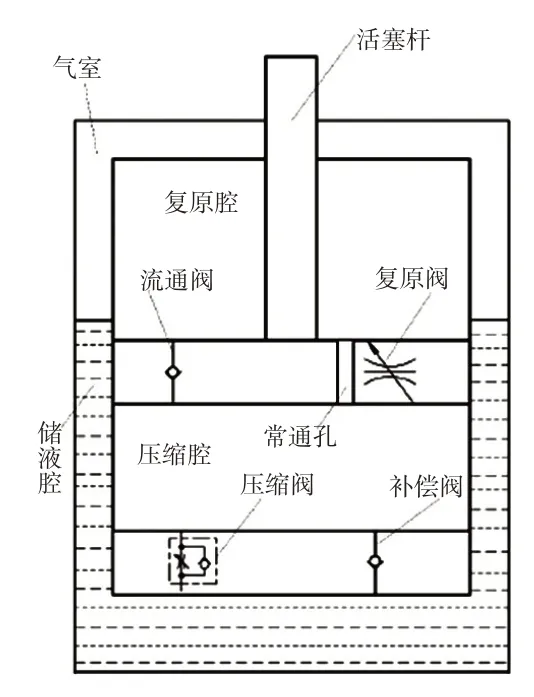
图2 减振器等效物理模型

2.2 数学建模

将减振器内部各结构作为整体，对活塞和活塞杆组成的整体进行受力分析，可以得到：

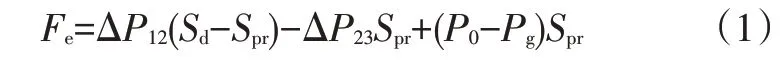
式中，Fe为活塞杆上受到的复原阻尼力；ΔP12为复原腔和压缩腔间的压强差，即活塞阀系的压强差；Sd为活塞截面积；Spr为活塞杆截面积；ΔP23为压缩腔与储液腔之间的压强差，即底阀系的压强差；P0为大气压强；Pg为气室内体压强。

设活塞杆系运动的距离为xe，将气体近似看作理想气体，根据理想气体方程PV=nRT（其中，P为气体压强，V为气体体积，n为气体的物质的量，R为比例系数，T为体系温度），并结合式（1），有：

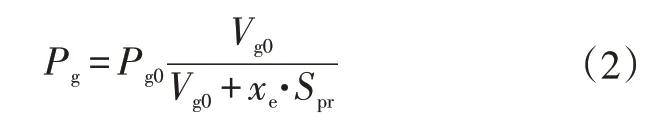
式中，Pg0、Vg0分别为气室内体的初始压强和气体体积。

补偿阀结构可简化为圆环平面缝隙模型，补偿阀上、下压强差为：

式中，μ为油液动力粘度；Rcv、rcv分别为补偿阀节流孔的外半径和内半径；δcv为补偿阀片偏移的距离，由于阀片的刚度和弹簧预紧力均很小，储液腔内液体压强很快就将大于预紧压强，因此可近似地看作阀片直接开启到最大偏移量状态，于是δcv为补偿阀片到底阀顶部的最大偏移量；Q23为流经补偿阀的油液密度，计算方式为：

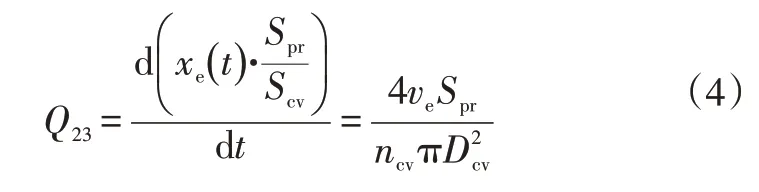
式中，Scv为补偿阀节流孔面积；ve为活塞杆系的运动速度；ncv、Dcv分别为补偿阀片槽的数量和液力直径。

联立式（1）～式（4），减振器复原行程阻尼力可以表示为：

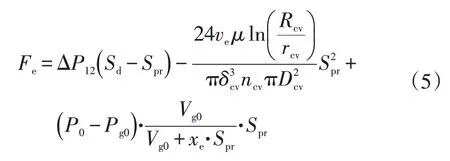
由式（5）可知：活塞杆面积在复原阻尼力的公式中各部分均出现，因此势必对阻尼力产生影响；气室压强也会对阻尼力产生影响；活塞阀系的压强差中，阀片的半径会对压强产生影响，且呈正相关，而阀片常通孔开口处的半径与阻尼力呈负相关，与阀片的当量厚度呈正比。根据对结构参数的初步分析，可以设定对复原行程阻尼力影响较大的具体参数为复原阀片的外半径、减振器活塞杆的直径和充入气室气体的初始压强。

3 补偿阀片运动仿真分析

利用减振器圆筒对称的特性，本文计算中均使用1/4流道模型，两侧墙壁设置为对称面，如图3所示。

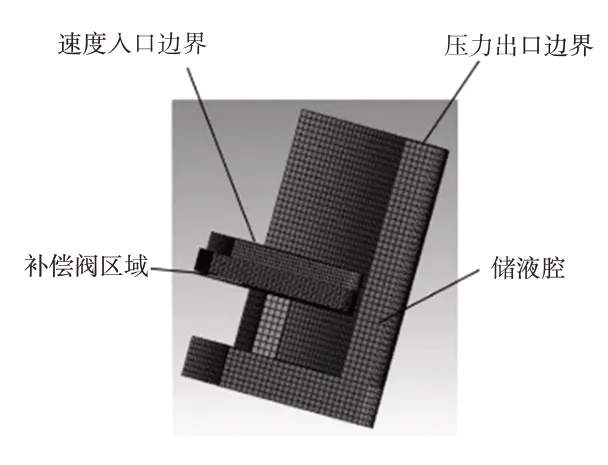
图3 阀片运动简化模型

3.1 计算模型

补偿阀片简化运动模型处理中，阀片处的处理较为重要。阀片初始时紧贴在压缩阀座上，因此阀片上、下的流场被阀片隔断，参考贺李平[10]对减振器液体模型的建立与局部处理，在阀片下方增加0.05 mm的液体预留层，使上、下流体区域相通，如图4所示。模型整体采用六面体网格进行划分，划分网格数量为12.6万个。

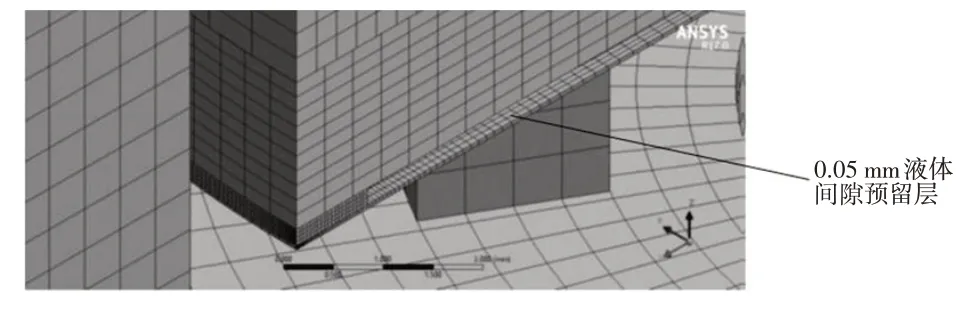
图4 液体间隙预留层示意

3.2 函数语言的建立

补偿阀片在流体力、弹簧弹力和预紧力的共同作用下运动，运动状态满足牛顿第二定律：

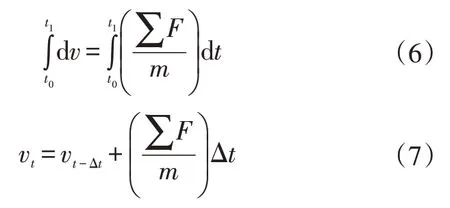
式中，v为补偿阀片速度；ΣF=F1-Fk-F0=F1-kxsp-F0为阀片上受到的合力；Fl为流体力，即油液作用在阀片上的力；Fk为弹簧弹力，由胡克定律可以得到；F0为初始预紧力；k为弹簧弹性系数；xsp为弹簧位移；m为补偿阀片质量；t0、t1分别为油液作用的起始时间点、终止时间点；vt为补偿阀片速度；Δt为油液作用的时间。

设定阀片运动的范围为0～1.5 mm，编写UDF程序，由于只有阀片的下表面（与油液最先接触的面）需要读取流体力并进行计算，在UDF程序中加入value_1函数，用于提取阀片下表面的速度并赋值给其他表面。

模型采用瞬态湍流模型，时间步长为5×10-5s，步数为100 步，迭代次数为5 次，出口边界压强为2×105Pa，流体入口速度随时间线性增长。

3.3 仿真结果分析

图5所示为流场在不同时刻的速度，随着时间的推进，油液流动速度增大，阀片下表面的冲击力增大，阀片逐渐向上移动。液体在阀片的综合作用力下形成射流，油液从侧壁处流出，但液体作用力不足以完全克服弹簧力，因此阀片仍有少量向下的速度场，在阀片上方形成了小规模的涡流。

图5 不同时刻流场速度矢量图

图6所示为流场在不同时刻的流线，流体从入口流入，经过储液腔和底部腔室汇聚到底阀节流孔的瓶颈处，通过节流孔后，挤压阀片向上，从阀片和管壁间的缝隙处流出。随着时间的推进，油液速度不断增大，但液体作用力不足以完全克服弹簧力，油液在阀片下方汇聚后向侧壁射出，阀片下方油液速度较大。

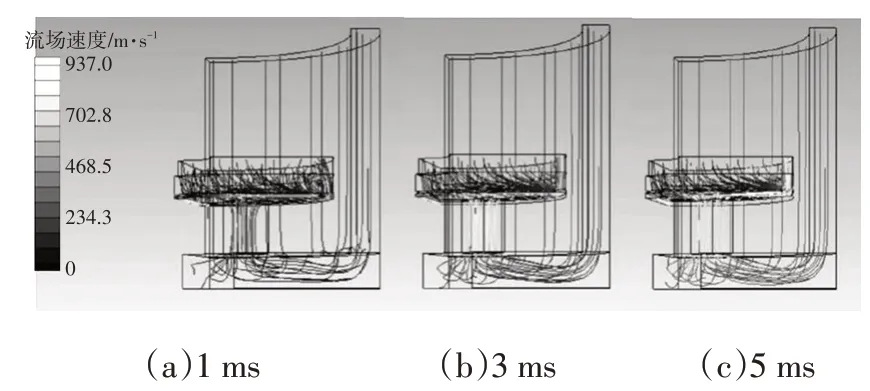
图6 不同时刻流场流线

图7所示为阀片下表面在不同时刻的压力，随着油液速度的增大，阀片下表面的压力逐渐增大，阀片的中间位置（正对底阀节流孔处）压力最大，这是节流孔的节流作用产生的，而靠近内侧管壁处油液压强也较大，并辐射向外逐渐减小。在节流孔出口附近出现了小范围的负压，且面积逐渐增大，这是由于阀片向上移动过程中在弹簧弹力的反作用力下出现振荡，油液压力不稳定造成的。

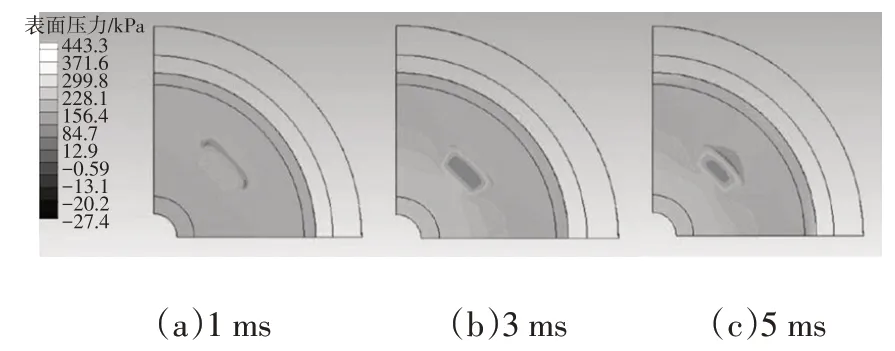
图7 不同时刻阀片下表面压力云图

通过对补偿阀片运动简化模型的模型处理、受力分析、UDF程序编写、边界条件设置和仿真分析，验证了动网格模型和UDF 程序的可行性，对仿真结果的分析验证了流体流动的方向和压强云图的正确性，结果表明，该简化原理模型可行。

4 复原阀片变形仿真分析

4.1 计算模型

利用减振器结构的对称性，建立减振器复原行程流道的1/4模型，采用全六面体网格对流道模型进行划分，网格数量为17.2万个，流道如图8所示。

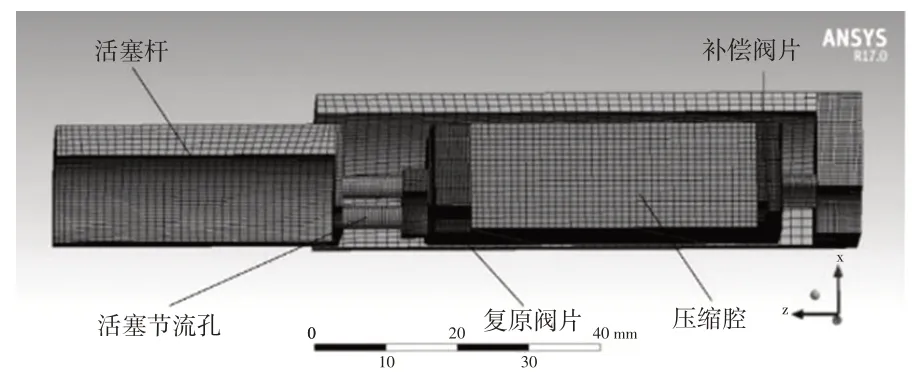
图8 1/4减振器复原行程流道模型

为了尽可能还原活塞节流孔的节流作用，在结构建模中保留活塞节流孔及其下方放大的液体层。划分网格后进行动网格的设置和边界条件的设置。仿真采用了正弦激励的方式，由于正弦函数具有周期性，本文只探究最初1/4周期的变化情况，参数如表1所示。

表1 激励函数、油液及氮气参数

流动采用k-ε模型和SIMPLEC算法计算，收敛精度为0.001，仿真步长为0.599 ms，步数为250步，总时长为150 ms。对活塞在节流孔内和补偿阀片在底阀上的运动网格进行设置，并用预览网格运动选项（preview mesh option）预先观察网格运动后的重构情况和质量情况。

4.2 仿真结果分析

图9所示为t=120 ms时的压力云图，复原阀片下方流体的压力最大，这是复原阀片的节流作用造成的，复原腔被压缩，但液体可以通过活塞上的节流孔流入复原腔，泄压口的存在使压强不会过大，而储液腔内的压强相对较小，这与上部气室内充入气体的压强有关。

图10 所示为1/4 减振器流场在复原行程中不同时刻的流场流线。在t=10 ms 时，活塞节流孔下方和底阀节流孔上方油液速度均较大，而复原阀片下方的流场处出现了涡流。活塞向上运动，活塞阀中液体受到挤压，通过活塞阀上的细圆孔流向活塞阀下部，同时油液从储液腔经底部腔室流入压缩腔，在补偿阀片处产生节流作用。在t=60 ms时，随着活塞阀的向上运动，补偿阀片上方也出现了涡流，且涡流不断增大，同时，油液在2处节流孔附近的速度减小。在t=120 ms 时，随着活塞上行，减振器内油液流速降低，节流孔下方的油液速度也趋于稳定，此时压缩腔内产生了比较大的涡流。

图9 t=120 ms时流场模型的压力云图

图10 流场流线图

图11 所示为不同时刻流场的速度，从活塞位置的变化和油液速度的变化可以看到，随着时间的推进，活塞杆上行速度逐渐减小，因此油液在工作缸内的流动速度减小。活塞阀中复原阀和底阀中补偿阀处油液的流动速度较大，这是阀片的节流作用造成的。阀片处所受压力增大时，阀片变形打开，更多油液流向压缩腔，产生更大的节流作用。

图11 流场速度矢量图

5 结构参数对阀片开度的影响

由于单向流固耦合是先计算完整的流场流动过程，再将流场内面上的力传递到固体域上进行静力学分析，也就意味着油液流场不会随阀片的变形而改变，因此无法模拟出减振器复原阀片从未开阀到开阀再到最大变形的整个过程。因此，本文通过探讨阀片在油液流场不同速度下的开阀情况，进而探究改变结构参数对阻尼力的影响。阀片的厚度为0.1 mm，材料选择为45 号结构钢，弹性模量为201 GPa，泊松比为0.27。

5.1 充入氮气的初始压强

图12 展示了阀片在油液速度为0.1 m/s 和0.25 m/s时复原阀在不同氮气初始压强下的变形情况。在v=0.1 m/s 时，初始压强为0.1 MPa 和0.4 MPa 的阀片变形量很小，此时认为阀片没有开阀，初始压强为3 MPa 的阀片已经开阀；在v=0.25 m/s 时，初始压强为0.4 MPa 和3 MPa 的阀片变形量相较于阀片的厚度均很大，此时认为阀片在开阀状态，而初始压强为0.1 MPa 的阀片变形量仍然很小，此时认为阀片未开。

图12 复原阀片在不同初始氮气压强下的变形云图

从图12 中可以看出：当初始压强为3 MPa 时，阀片在v=0.25 m/s 时所受压力过大，这样可能使阀片的寿命降低，还有可能引起畸变现象，因此充气压力不应过大；当初始压强为0.1 MPa 时，阀片的变形量不足以打开阀片，因此减振器可能达不到设计所需提供的阻尼力，车辆在道路上行驶十分危险，因此初始充入气体也不应过小。根据经验总结和试验测试，氮气初始压强应在0.4～0.6 MPa 范围内，才能使充入的氮气发挥应有的增加回弹力和降低噪声的作用。同时，根据阀片变形量的分析可得，初始压强越大，阻尼力越小。

5.2 活塞杆直径

图13 展示了复原阀片在v=0.2 m/s 和v=0.25 m/s 时活塞杆直径分别为8 mm、10 mm和12 mm的变形情况，从图13 中可以看出：复原阀片的变形量随着活塞杆直径的增大而减小，这意味着活塞杆直径越大，阀片开阀时的速度越快，也就意味着减振器阻尼力进入开阀后的第2、第3阶段变慢，而所对应的第1阶段末阻尼力大小几乎相同（由于腔室内压强相差无几），则在同等激励条件下第3阶段末能达到的阻尼力也会变低，故减振器活塞杆直径越大，复原行程产生的阻尼力越小。因此，活塞杆直径与阻尼力呈负相关。

图13 复原阀片在不同活塞杆半径下的变形云图

5.3 复原阀片外半径

图14 展示了复原阀片在v=0.2 m/s 和v=0.25 m/s 时复原阀片外半径为12 mm、10 mm 和8 mm 时的变形情况，从图14中可以看出，阀片的变形随着复原阀片半径的减小而增大，且变化很明显。这是由于随着阀片半径增大，阀片的刚度随之增加，更不容易产生变形，且半径增大后相对应的流体层油液的体积变小，因此，更少的油液能够通过阀片，但同时油液速度也在不断增加，因此会产生更大的节流作用力。因此，复原阀片外半径的增大会带来开阀速度的减慢，则复原阻尼力更大，这一结论与理论分析相一致，进一步验证了复原阀片半径与阻尼力正相关的关系。

6 结束语

本文对减振器复原行程阻尼力进行数学建模，用局部结构的等效流场模型求得复原阻尼力的公式，初步确定了影响阻尼力的3 个结构参数：复原阀片外半径、活塞杆直径以及充入气室气体的初始压强。通过对补偿阀片运动过程简化原理模型的建模、简化和仿真分析，验证了UDF 程序的可行性和流场油液运动方向正确性；通过对流线图、速度矢量图、压力云图和补偿阀片位置的分析，验证了仿真的可操作性。