电动车用永磁同步电机定子铁心固有频率研究＊

骆开军 林曦鹏 陈海生,2 梁志松 张少朋

（1.国家能源大规模物理储能技术（毕节）研发中心，毕节 551700；2.中国科学院工程热物理研究所，北京 100190）

主题词：定子铁心 固有频率 有限元法 频谱分析

1 前言

永磁同步电机的各阶次径向电磁力与径向模态是决定电机振动噪声的关键因素[1-2]，准确预测电机定子铁心的固有频率和减小径向电磁力幅值对有效抑制电机的振动和噪声至关重要[3-4]。国内外学者对电机模态展开了深入研究，S.Noda 等学者利用解析分析快速得出定子铁心的固有频率[5]，王天煜利用有限元分析方法分析了端盖和底脚对大型异步电机固有频率的影响[6]，于慎波利用有限元与解析法分析电机定子圆柱壳体长度、壁厚、平均直径和径厚比对其周向模态频率的影响[7]，文献[8]～文献[10]采用解析法针对开关磁阻电机、超声波电机和小型感应电机的固有频率进行了研究。

上述研究未针对定子铁心材料属性和结构参数对定子铁心固有频率的影响进行研究。本文对永磁同步电机进行简化建模，采用解析与有限元法计算电机定子的固有频率，并对电机开展空载噪声试验，用噪声频谱数据间接验证电机模型的准确性，并根据解析法分别计算不同材料属性、定子齿宽、轭厚和定子铁心轴向长度条件下的固有频率，研究不同参数对固有频率变化的影响，为抑制电机共振提供理论依据。

2 电机定子固有频率等效解析模型

模态分析的关键是确定结构系统动态特性的描述参数。根据Hamilton 应力-应变、应变-位移的关系，可得出电机机构的运动方程[11-13]：

式中，K为刚度矩阵；M为质量矩阵；R为阻尼矩阵；μ、分别为节点的位移矢量、速度矢量、加速度矢量；F为节点力矢量。

对电机进行模态分析时，忽略阻尼，同时令F=[0]，时间导数用jω代替，其中ω为角频率，则式（1）简化为：

根据线性方程组理论，有非零解的充分必要条件为|K-ωr2M|=0，解出满足以上方程的频率ωr和对应的非零向量μr，则结构的固有频率f为：

式中，Ki、Mi分别为铁心的刚度和质量。

电机定子铁心上有绕组线圈、定子槽等，不是完整的圆柱体。为了计算定子铁心的刚度和质量，将定子齿等效成为长方形，定子轭等效成圆柱，则铁心刚度和质量为：

式中，Ii为截面惯性矩；m为轴向阶数；Li为定子铁心轴向长度；Ei为弹性模量；hi为定子轭厚度；Ri为定子铁心平均半径；Vi为泊松比；ρi为铁心密度；Ct为定子齿宽度；Z为槽数；R1、R2分别为定子铁心内、外半径；为二阶运动特征方程的根；为无量纲的壁厚因子。

3 电机定子的模态分析

3.1 电机定子结构的有限元模型

本文的研究对象为某8极36槽永磁同步电机，其定子铁心槽为一种梨形半封闭槽，为简化分析，在建立电机定子铁心有限元模型时忽略对结构刚度影响较小的小孔和倒角，并将绕组质量等效到定子齿上。电机定子铁心参数如表1所示，定子铁心有限元模型如图1所示。

表1 电机定子铁心参数

图1 定子铁心的有限元模型

定子铁心和绕组的材料分别是硅钢和铜，材料参数如表2所示。

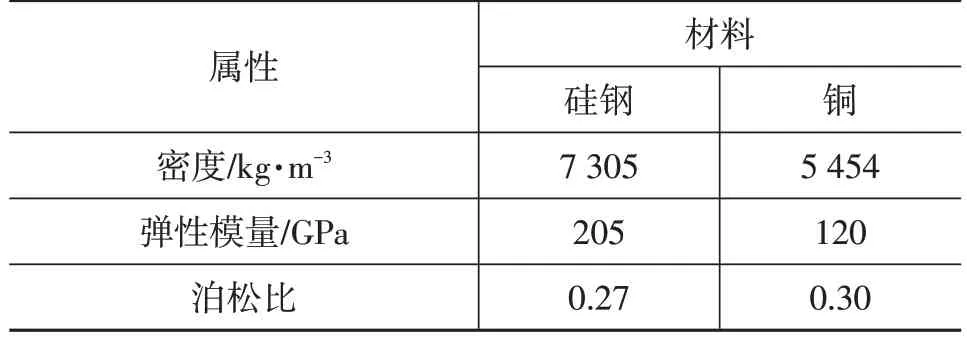
表2 定子材料特性

3.2 定子铁心模态分析

根据电机等效解析模型计算0～5 000 Hz 频率下电机定子结构的固有频率，其2 阶～5 阶固有频率分别为568.84 Hz、1 276.56 Hz、2 865.23 Hz、4 386.41 Hz。

有限元模型计算得到的定子铁心自由振动下固有频率振型如图2 所示，根据图2 可知，2 阶振型为椭圆形，3阶振型为三角形，4阶振型为四边形，5阶振型为五边形。

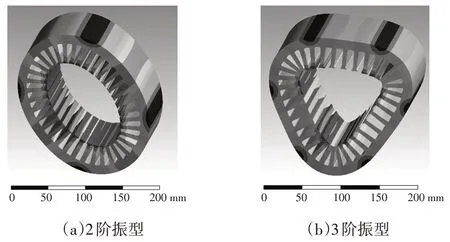
图2 模态振型

3.3 定子铁心谐响应分析

根据定子铁心模态分析结果，采用有限元分析法对0～5 000 Hz范围内的频率进行谐响应分析，得出定子表面位移随频率的变化曲线如图3所示。

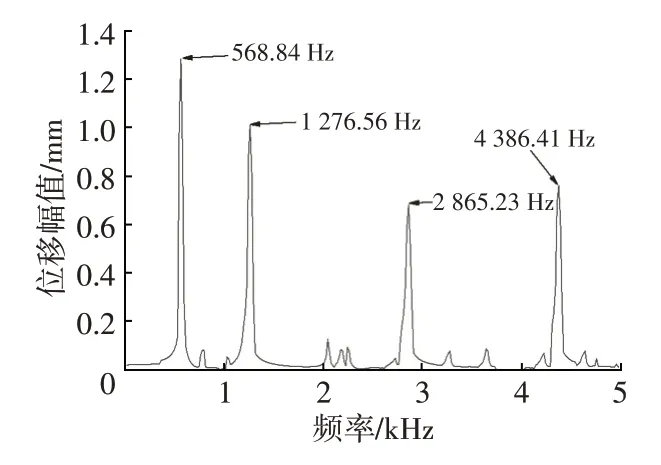
图3 定子表面位移变化

由图3 可知，定子在固有频率568.84 Hz 时的振动位移最大，当电机激振力的频率与568.84 Hz相近时，电机产生的共振比其他固有频率下产生的共振强。

3.4 定子铁心固有频率解析计算

采用等质量法将绕组的质量按槽满率等效在定子齿上，将质量等效后，其定子齿的密度为：

式中，m1、m2分别为定子齿和绕组的质量；V为定子齿体积。

根据式（3），利用等效后定子齿的密度计算定子铁心的固有频率，并与有限元计算结果对比，结果如表3所示。

表3 解析法与有限元法固有频率计算误差对比

由表3可知，质量等效后计算得到的解析解与采用真实结构和材料密度计算的有限元法结果吻合良好。

4 电机空载噪声频谱分析

作用于电机定子表面上的径向电磁力频率与电机定子固有频率相近时，会引起电机共振。本文开展电机空载噪声测试，通过噪声频谱图得出电机的噪声频率，并与电机定子结构固有频率相比较，间接验证电机解析法和有限元法计算固有频率的准确性。

为了确保电机噪声值的精确性，在刚性地面铺设泡沫垫，将电机置于泡沫垫上，可有效抑制测试电机与刚性地面间的振动对电机空载噪声测试误差的影响，并将声级计置于距离电机表面1 m 处进行电机噪声采样，如图4 所示，采用丹麦BK 声级计测量电机在0～2 000 r/min 转速下的空载噪声，结果如图5 所示。

图4 电机噪声现场测试

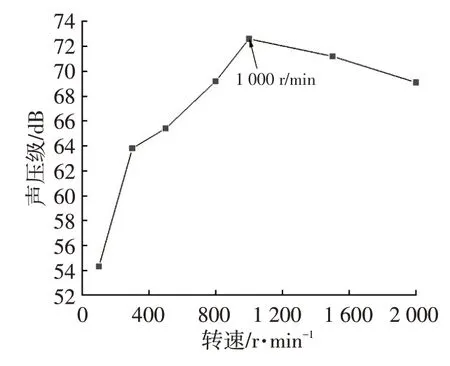
图5 电机空载下噪声与转速的关系

由图5可知，随着电机转速的提高，噪声逐渐增大，当转速达到1 000 r/min 时，噪声声压级达到最大值，测试过程中出现刺耳的声音，随着转速继续增加，噪声声压级逐渐减小。

根据试验数据，提取出电机转速为1 000 r/min、2 000 r/min时的空载噪声频谱如图6所示。由图6可知，2 种转速下分别存在32 Hz、560 Hz、1 168 Hz、4 208 Hz以及1 104 Hz、4 400 Hz 的峰值噪声频率。图6a 中的32 Hz 噪声频率由电机旋转频率引起，图6a、图6b 中其余噪声频率可能与电机定子铁芯固有频率相近，由电机共振引起，表4 所示为噪声频率、解析法频率结果的对比。

由表4可知，解析法计算的固有频率与空载噪声频率比较，误差很小，表明电机解析模型具有较高的准确性。

图6 不同转速下空载噪声频谱

表4 噪声频率、解析法频率比较

5 定子铁心参数分析

模态计算采用的物理模型参数见表1 和表2，通过改变定子铁心的材料属性参数、定子齿宽、定子轭厚、定子轴向长度来分析相应参数对定子铁心固有频率的影响。

5.1 材料属性对定子铁心固有频率的影响

通过保持定子铁心的其他参数不变，单独改变定子轭的弹性模量、密度或泊松比研究相应参数对固有频率的影响。固有频率随定子轭弹性模量、密度的变化趋势分别如图7、图8所示。

由图7可知，固有频率随着弹性模量的增加呈上升趋势。由图8 可知，随着定子轭密度的增加，固有频率呈下降趋势，但下降幅度不大。为进一步研究密度与固有频率的关系，引入同一模态阶次下不同定子轭密度固有频率的相对率β，即对应阶次固有频率变化值与其密度变化值的比率：

式中，fi为各阶固有频率；ρi为fi下对应的定子轭密度，其结果如图9所示。

图7 固有频率随定子轭弹性模量的变化趋势

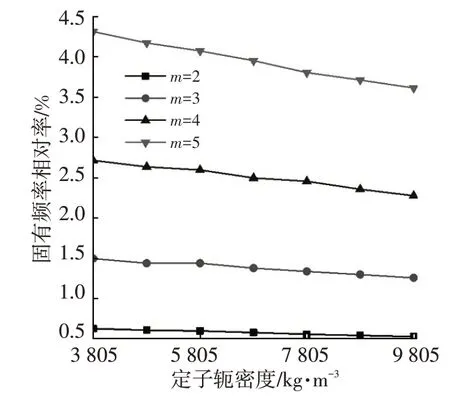
图8 固有频率随定子轭密度的变化趋势

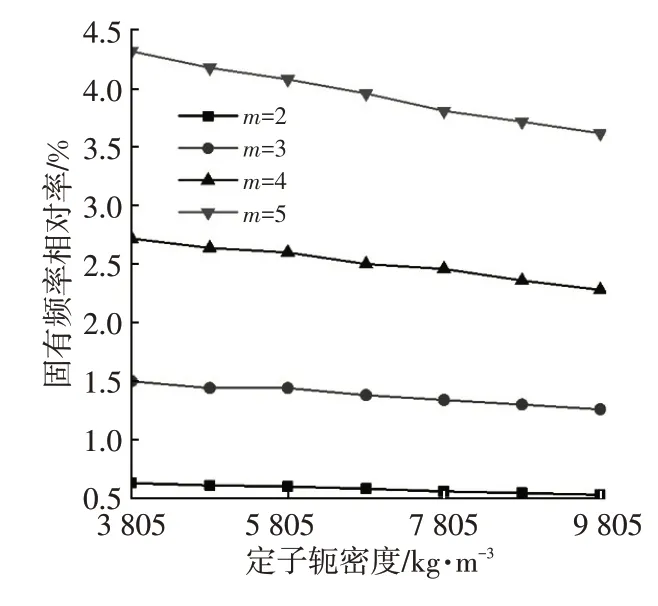
图9 不同定子轭密度的相对变化率

从图9 可以看出，随着定子轭密度的增加，同一模态阶次下固有频率相对率有所下降，定子轭密度对固有频率的影响很小。

定子轭泊松比与固有频率间的关系如图10 所示。由图10 可以看出，固有频率随着泊松比的增加基本保持不变，泊松比对固有频率的影响几乎可忽略不计。

5.2 定子齿宽对定子铁心固有频率的影响

单独改变定子齿宽来研究其对固有频率的影响，结果如图11所示。

由图11可知，随着定子齿宽的增加，固有频率稍有下降，但幅度不大，主要是因为定子铁心质量和刚度随着定子齿宽的增加而增加，两者对固有频率的影响相互抵消，使得定子齿宽对固有频率的影响较低。

图10 固有频率随定子轭泊松比的变化趋势

图11 固有频率随定子齿宽比的变化趋势

5.3 定子轭厚对定子铁心固有频率的影响

单独改变定子轭厚研究其与固有频率的关系，结果如图12所示。

图12 固有频率随定子轭厚的变化趋势

为深入研究定子轭厚与固有频率的关系，引入比例系数，即将同一模态阶次不同弹性模量下的固有频率差值与对应弹性模量差值的比值：

式中，fj为弹性模量Ej下对应的固有频率。

为了研究方便，取Ej=200 GPa，根据式（8）得出其结果如图13所示。

从图13中可以看出，随着定子轭厚的增加，比例系数呈上升趋势，因此定子轭厚越大，固有频率相对于初始模型固有频率的变化越大。

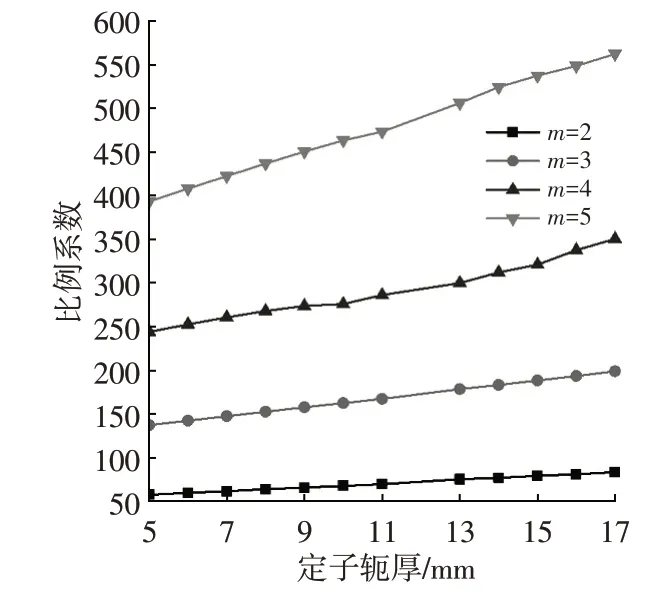
图13 不同定子轭厚的比例系数

5.4 定子轴向长度对定子铁心固有频率的影响

同理，通过单独改变定子铁心轴向长度研究其与固有频率的关系，结果如图14所示。由图14可知，固有频率不随定子轴向长度的变化而变化。

图14 固有频率随定子轴向长度的变化趋势

6 结束语

本文以8极36槽永磁同步电机为研究对象，建立电机定子铁心结构的三维有限元模型，经过有限元法分析、解析法分析与电机空载噪声试验得出以下结论：

a.有限元法与解析法计算出的定子铁心固有频率结果基本吻合，电机空载噪声试验间接验证了定子质量等效法计算铁心解析法模型的准确性。

b.分析定子铁心材料属性、定子齿宽、定子轭厚、定子铁心轴向长度对固有频率的影响，结果发现，弹性模量和定子轭厚对固有频率的影响最大，因此，在保证定子性能的基础上，可以考虑调整定子轭厚改变固有频率，抑制电机共振。