Characteristic Length of Metallic Nanorods under Physical Vapor Deposition

Kai Jun | Bo-Jun Wang | Hai-Yuan Chen

Abstract—By using physical vapor deposition (PVD) to grow metallic nanorods, the characteristic length is controllable, which can be identified by two different growth modes: Mode I and Mode II.In Mode I, the growth of metallic nanorods is dominated by the monolayer surface steps.Whereas in Mode II, the growth mechanism is mainly determined by the multilayer surface steps.In this work, we focused on the analysis of the physical process of Mode I, in which the adatoms diffuse on the monolayer surface at beginning, then diffuse down to the next monolayer surface, and finally result in the metallic nanorods growth.Based on the physical process, both the variations of the characteristic length and the numerical solutions were theoretically proposed.In addition, the twodimensional (2D) lattice kinetic Monte Carlo simulations were employed to verify the theoretical derivation of the metallic nanorods growth.Our results pay a new way for modifying the performance of metallic nanorods-based applications and devices.

1.lntroduction

Metallic nanorods have been studied widely, which have broad prospects in optical devices, sensors,biomedicine, and catalysts[1]-[3].However, the properties and applications are generally affected by the changes of the characteristic length and surface morphology.Therefore, the investigation of the characteristic length of metallic nanorods is of significant interest to both simulations and experiments.By using physical vapor deposition (PVD) to grow metallic nanorods[4]-[6], the characteristic length and surface morphology can be regulated[7],[8].Generally, there are two types of growth models for metallic nanorods by PVD[9]: Mode I is taking place on the wetting substrate,however, Mode II is occurring on the no-wetting substrate[10].In Mode I, the growth of nanorods primarily depends on the adatoms diffusing in the monolayer and down to the next nearest monolayer surface.Whereas, Mode II mainly relies on the multilayer surface steps that limit the diffusion of the adatoms[11].Therefore, in the absence of chemical reaction, the physical process of diffusion is the dominant factor in the growth of metallic nanorods[12].

Mode II leads to the successful preparation of the smallest diameter of the metallic nanorods in our previous study[11], because of the complete or nearly complete shadowing beneath the upper most layer.Comparing with the monolayer surface steps, the multilayer surface steps with a large three-dimensional (3D) Ehrlich-Schwoebel (ES)diffusion barrier play a dominant role in the growth process and limit the diffusion of the adatoms[13]-[15].The smallest diameter theory of metallic nanorods in Mode II has been established and the theoretical result of the smallest diameter iswherenis the number of layers of the metal nanorods,V3Dis the diffusion jump rate of the adatoms over multilayer surface steps,αis the probability of the adatoms jump to the next step, andFeis the effective deposition rate on the top of the nanorod.Besides, the theory is verified by the lattice kinetic Monte Carlo simulations and PVD experiments[11].

For Mode I, the characteristic length of metallic nanorods has been described by a closed theory[9], which is derived from a wedding cake model for the growth of thin films[16]-[18]and verified by the lattice kinetic Monte Carlo simulations.This closed theory provides a bridge for the growth of thin films to be transformed into the growth of nanorods by Mode I[19],[20].However, the details describing the physical process of growing metallic nanorods in the closed theory by Mode I are absent.Due to the absence, it is eager to comprehensively describe the metallic nanorods growth by Model I.In the physical process of the metallic nanorods growth of Model I, the monolayer epitaxial growth leads to a larger diameter than that by Mode II[10].This epitaxial growth is stemmed from the adatoms diffusion, which can overcome the smaller two-dimensional (2D) ES barrier and then diffuse down to the next monolayer surface[21],[22].

In this paper, we established a simple growth model by analyzing the physical growth process of Model I, which can be utilized to simulate the variation of the characteristic length and obtain the numerical solutions.By analyzing the physical process of the adatoms in the monolayer of metallic nanorods in Mode I, the mechanism of the monolayer growth in metallic nanorods growing was discovered, i.e., the adatoms diffuse on the monolayer surface and then down to the next monolayer surface.Based on the mechanism, the changes of the characteristic length and the numerical solutions in Mode I were achieved.Finally, the theoretical derivation was verified by the 2D lattice kinetic Monte Carlo simulations.

2.Results and Discussion

Firstly, we proposed a simple growth model with schematic descriptions by theoretically analyzing the growth process of metallic nanorods in Mode I.Secondly, the changes of the characteristic length and the numerical solutions were theoretically derived.This derivation is based on the approximation of the quasi-steady state and perfect nucleation.Finally, the copper (Cu) was considered as an example to simulate the growth of metallic nanorods by the 2D lattice kinetic Monte Carlo simulations, where the numerical results agreed well with the theoretical derivation.

2.1.Growth Process

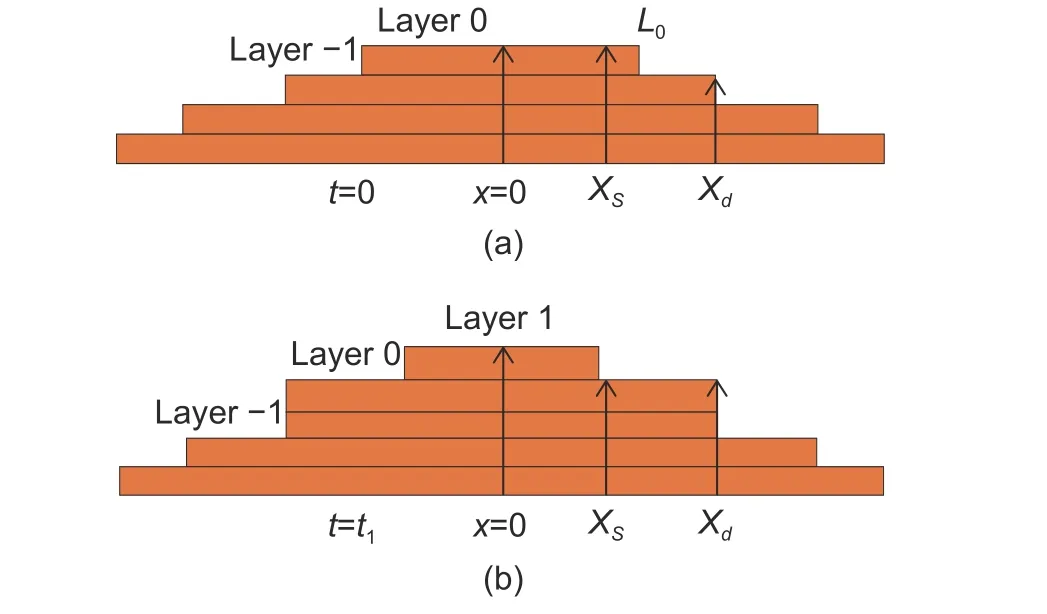
Fig.1.Simple growth process of metallic nanorods: (a)shadowing effect happening at time t=0 and (b) Layer 0 reaching the length of Layer -1 at time t=t1.

Based on Mode I, we studied a simple case of the step-dynamic mechanism as shown in Fig.1.At timet=0, when the shadowing effect happens, the shadowing pointXSlies on the upper most layer, i.e.,Layer 0.All the layers underneath will remain unchanged.As shown in Fig.1 (a), sinceXSis less than the length of Layer 0,L0, there exists a possibility that Layer 0 will reach the length of Layer -1 before the newly formed Layer 1 reachingXS.Furthermore, two monolayer steps will collapse and form a new multilayer step at the positionXd, as shown in Fig.1 (b).According to the growth mechanism of Mode I,Xdis the final diameter of nanorods determined by the length of Layer -1 at timet=0.

2.2.General Theory

Following by previous discussion, the simple model in subsection 2.1 can be extended to a more general case (as shown in Fig.2): Layer -1 is large enough so that before Layer 0 catching up with it, the new Layer 1 reaches the shadowing pointXSand Layer 0 is shadowed.In another word, the finalXdis smaller than the size of Layer -1.Since the layers under Layer 0 are completely shadowed fromt=0, those layers beneath Layer 0 in Fig.2 will be not taken into account.

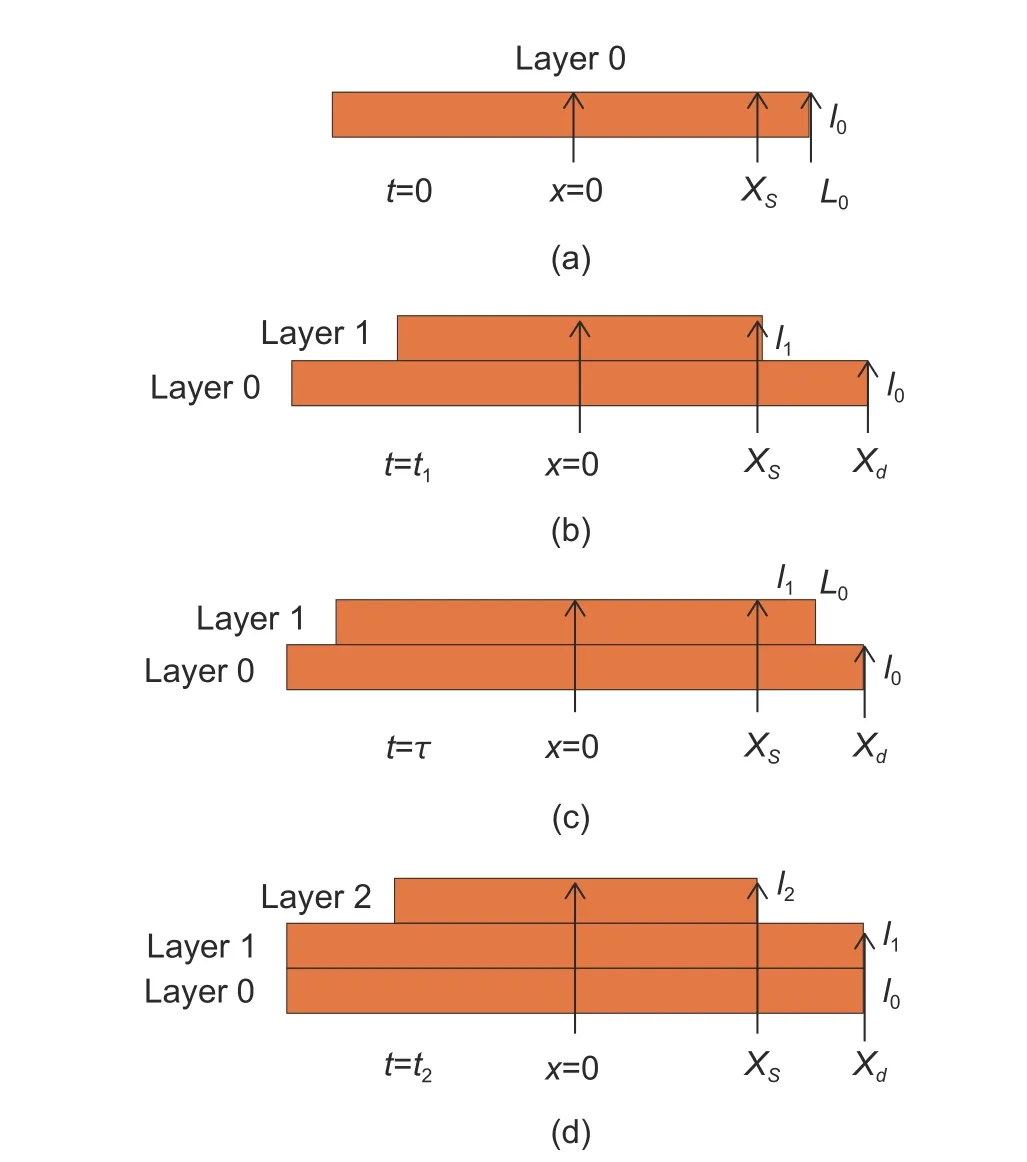
Fig.2.Step dynamics in a more general case: (a) shadowing effect happening at time t=0, (b) Layer 0 reaching the length of Layer -1 at time t=t1, (c) new monolayer appearing at time t=τ (τ represents the average time), and(d) Layer 1 reaching the length of the Layer 0 at time t=t2.

Assume that the shadowing boundaryXSis on the layers.As shown in Fig.2 (a), we set the time point when Layer 1 just nucleates ast=0 and so the length of Layer 0 is 2L0.With the increase of time, Layer 0 will still become elongated.On Layer 0, with the approximation of the quasi-steady state, when timetgoes from 0 tot1, we define the half length of Layer 1 and Layer 0 to bel1(t) andl0(t), respectively.It is noted that the metallic nanorods are completely symmetric in the growth process.With the increase of growth time,the effective area of the adatoms on the surface of Layer 0 gradually decreases, so the average deposition rateF0of the adatoms on Layer 0 isF0=F[(XS−l1(t))/(l0(t)−l1(t))], whereFis the deposition rate.The concentration distribution of Layer 0 can be calculated by using the Tersoff’s theory on the critical size of island[16]as shown in (1):

wheren0is the concentration distribution of deposited atoms in Layer 0 andDcis the diffusion constant.

According to the approximation of perfect nucleation, the adatoms diffuse down to the next monolayer surface and nucleate directly at the kink of the step.The boundary conditions can be expressed as: Whenx=l1(x), thenn0(x)=0; whenx=l0(x), then dn0(x)/dx=−αn0(x).Here,α=−exp[−(EES−ED)/kT] withkTbeing the Boltzmann factor, which is the probability per unit time that the adatoms diffuse to the next monolayer surface[16].For the reason that the growth of Mode I depends on the monolayer surface steps,EESis considered as the 2D ES diffusion barrier andEDis the diffusion barrier on the surface.

From (1) and the boundary conditions, the concentration distribution at Layer 0 is derived as

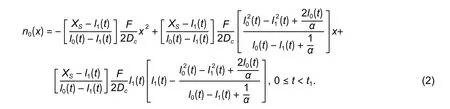
As for Layer 1, it grows initially at timet=0 and there is no shadowing effect in the time period from 0 tot1, so the deposition rate of adatoms isF.Since Layer 2 does not appear in this period, the adatoms hop to the edge of Layer 1 and then diffuse to Layer 0.These adatoms will result in the growth of Layer 1, so the boundary conditions can be expressed as: Whenx=0, then dn1(x)/dx=0; whenx=I1(t), then dn1(x)/dx=−αn1(x).Meanwhile, the concentration distribution of the adatoms in Layer 1 can be expressed as

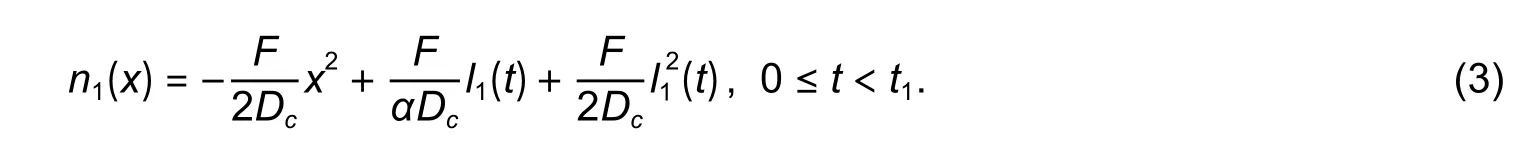
During the period fromt1toτ, because Layer -1 is large enough, the newly emerged Layer 1 has reachedXSand Layer 0 is completely covered before Layer 0 catching up with Layer -1.As for Mode I, it depends on the monolayer surface steps and only a few adatoms can overcome the multiple step barriers and jump off the edge.Therefore, the length of Layer 0 remains unchanged, and this size is the final diameter of the metallic nanorods, i.e., 2Xd.At timet1shown in Fig.2 (b), Layer 1 grows to the shadowing pointXSand Layer 2 does not appear in this time period.Thus, the adatoms will be deposited only on Layer 1.Besides, Layer 1 will become elongated.The average deposition rate of the adatoms isXSF/l1(t),and the boundary conditions are whenx=0, then dn1(x)/dx=0; whenx=I1(t), then dn1(x)/dx=−αn1(x).So the concentration distribution of the adatoms in Layer 1 is

At timeτ, Layer 2 occurs to grow and Layer 1 has grown toL0, as shown in Fig.2 (c).Between the time periodτtot2, Layer 1 will repeat the growth process of Layer 0 happened during the period from 0 tot1until it grows toXdat timet2, as shown in Fig.2 (d).For Layer 2, the complete growth process will be the same as that of Layer 1.It is assumed that timet=0 is just the time point when Layerm(1 ≤m≤n) appears.Hence, based on (2) to (4), the concentration distribution of the adatoms deposited on Layermduring the period from 0 tot2can be summarized as

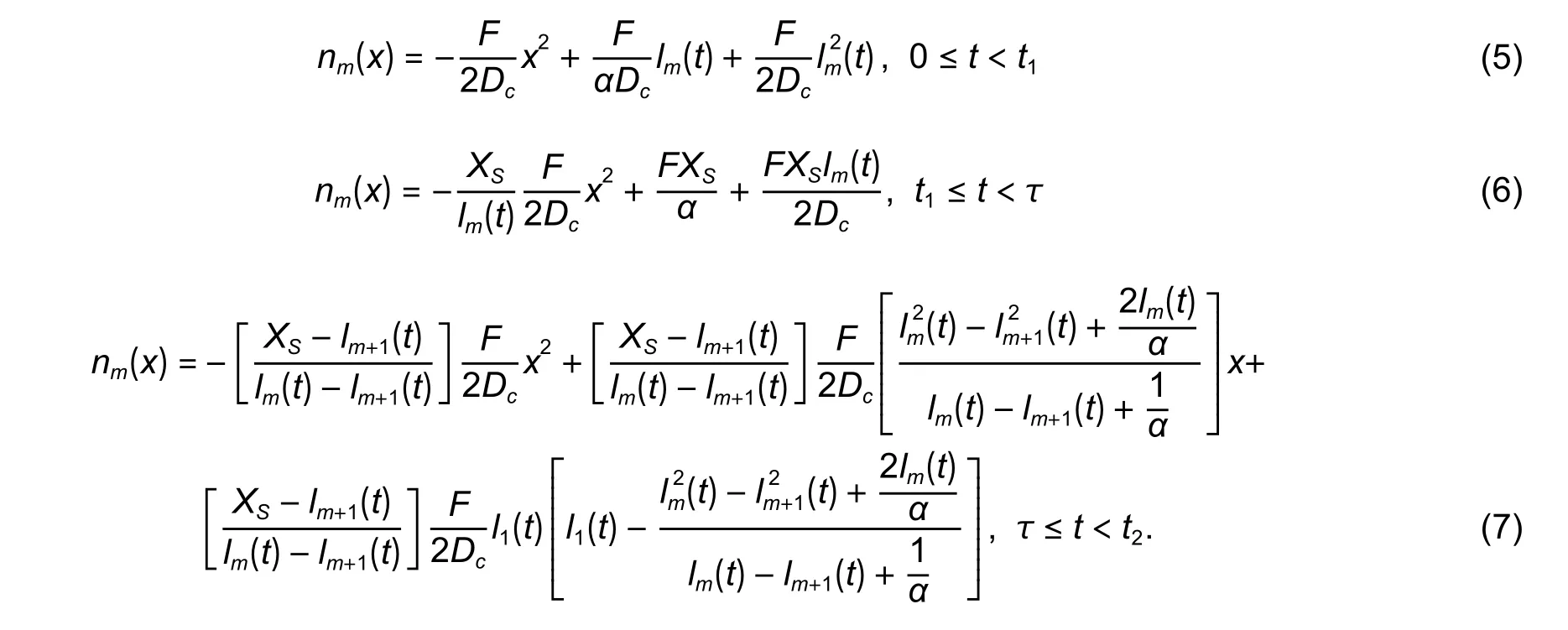
Here we defineSmas the rate of the adatoms from themth monolayer diffusing down to the (m-1)th monolayer.Due to the assumption of perfect nucleation, these adatoms will be nucleated and grow in themth monolayer.The expression forSmis

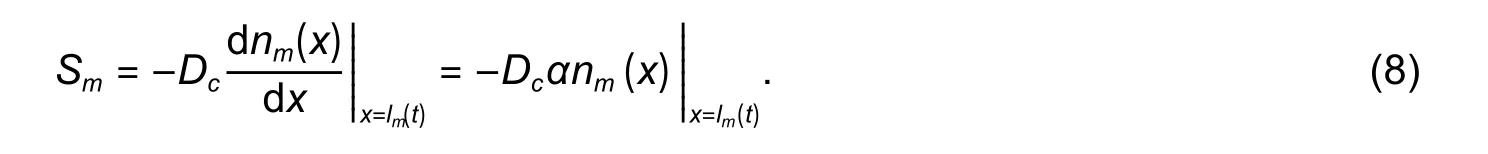
According to (5) to (8), the rates of the adatoms at the edge of themth monolayer diffusing down to the (m-1)th monolayer in different growth periods are summarized as

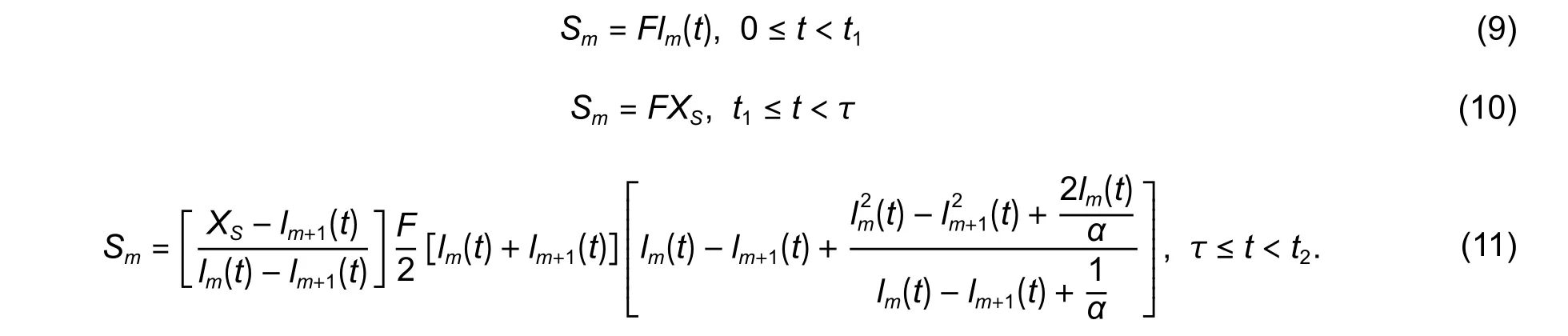
According to (9) to (11) and the total amount of the adatoms deposited on the (m-1)th monolayer per unit timeF[XS−Im(t)], the growth rates of themth monolayer in the whole growth process can be obtained as

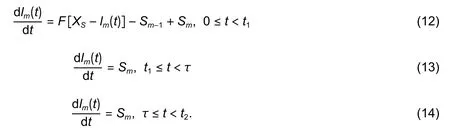
According to the lone adatoms model[23], the average time is[24]

whereV2Dis the diffusion jump rate of the adatoms over monolayer surface steps.

According to (12) to (15), we can describe the variation of the characteristic length of metallic nanorods with time.From this characteristic length-time relationship, the final diameter of metallic nanorods can be acquired.

2.3.2D Lattice Kinetic Monte Carlo Simulations

Because the 2D lattice kinetic Monte Carlo simulations involve the crucial diffusion process in the whole growth including the diffusion on the same monolayer, down to the next monolayer, and multilayer diffusion.Hence, the 2D Monte Carlo method was utilized to verify the theoretical derivation of the characteristic length for metallic nanorods.

In the simulations, we chose Cu as the deposition atoms.The deposition rate, temperature, and the size of the metallic substrate areF=1 nm/s, 100 K, and 40 lattice units, respectively.Owing to the shadowing effect, only specific portions of the substrate are injected with Cu, so the deposition range is given as 12 lattice units, which has the reflection symmetry, i.e., the position of the shadowing pointXSis 6 lattice units.In previous studies, the adatoms diffusion barrier on a flat surface of nanorods was 0.06 eV[13],[15].Meanwhile, the adatoms diffusion barriers over a monolayer and multilayer step were 0.16 eV and 0.40 eV, respectively[13],[15].The prefactor of the diffusion frequency was reported as 5×1011s−1in the previous study[25].

As shown in Fig.3, it is the entire process of the change of the characteristic length of metallic nanorods.In the initial stage of the monolayer growth, the monolayer surface has no shadowing effect.The main mechanism of the monolayer growth is the diffusion and nucleation of Cu atoms deposited on the surface of the monolayer.Only a small part of the Cu atoms can overcome the 2D ES barrier and diffuse to the next monolayer, leading to the monolayer growth.The contribution to the monolayer growth of this part is weaker than that of the diffusion and nucleation of the Cu atoms on the monolayer.Therefore, the growth trend of the metallic nanorods in the early growth stage behaves a linear relationship.When the monolayer grows to the shadowing point, the shadowing effect begins to affect on the surface of the monolayer and the effective deposition size on the surface of the monolayer is reduced, so that the atomic action of the diffusion nucleation portion on the monolayer is gradually weakened during the growth process.Until a new monolayer appears, this weakness is becoming more obvious.Meanwhile,the growth of the monolayer in which the adatoms overcome the 2D ES barrier and diffuse to the next monolayer gradually becomes pronounced, so the gradient of the growth curve changes.When this new monolayer grows to the shadowing point, all layers under this new monolayer are masked, and no deposition is injected, so the monolayer diameter will not change.

Fig.3.2D lattice kinetic Monte Carlo simulations of the change process of the Cu nanorods characteristic length.

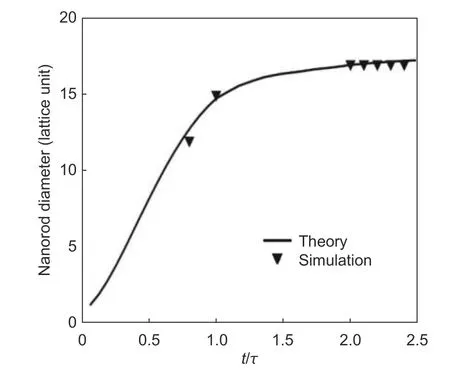
Fig.4.Theoretical variation curves of the Cu nanorods characteristic length comparing with the simulation.

Since the relationship between the number of deposition steps and the characteristic length of the metal nanorods is obtained in the simulation results, in order to obtain a comparison between the simulation and theory,t/τcan only be calculated at a certain length.From this point, the growth of the metallic nanorods from the shadow point at timet1to the time when the new single layer appears atτis targeted.Besides, another five points are gotten where the final diameter of the metallic nanorods is nearly unchanged,which is shown in Fig.4.From Fig.4, the results between the simulation and theory show great agreement.However, it is noted that the perfect nucleation and quasi-steady-state conditions were utilized in the calculation process and the 3D step barrier is considered as infinite.The 2D lattice kinetic Monte Carlo simulated diameter of the metallic nanorods is slightly different from the theoretical one, when the diameter of the metallic nanorods grows to the shadowing point and the new monolayer appears.However, the theoretical derivation of the growth process of metallic nanorods in general is consistent with its simulated growth process.

3.Conclusions

In summary, by analyzing the physical diffusion process of the adatoms on monolayers during the growth of metallic nanorods in Mode I, we have established a simple model to reveal the process in details for the growth of metallic nanorods.The variations of the characteristic length and final diameter of metallic nanorods were theoretically derived in Mode I.Then the theoretical derivation of the characteristic length of metallic nanorods was verified by the 2D lattice kinetic Monte Carlo simulations, which showed good agreement.Our results provide a new view to better understand the mechanism of the metallic nanorods growth, which have a great impact on the metallic nanorods-related applications and devices.

Disclosures

The authors declare no conflicts of interest.