ECC-Based RFlD Authentication Protocol

Xing-Chun Yang | Chun-Xiang Xu | Chao-Rong Li

Abstract—The radio frequency identification (RFID) technology has been widely used so far in industrial and commercial applications.To develop the RFID tags that support elliptic curve cryptography (ECC), we propose a scalable and mutual authentication protocol based on ECC.We also suggest a tag privacy model that provides adversaries exhibiting strong abilities to attack a tag’s privacy.We prove that the proposed protocol preserves privacy under the privacy model and that it meets general security requirements.Compared with other recent ECCbased RFID authentication protocols, our protocol provides tag privacy and performs the best under comprehensive evaluation of tag privacy, tag computation cost, and communications cost.

1.lntroduction

As the fundamental technology of the Internet of things, the radio frequency identification (RFID) technology has been widely used in domains, such as supply chain management, object identification, and access control systems.The hardware of a typical RFID system comprises tags, readers/interrogators, and a back-end server.RFID tags are resource-constrained devices that support bitwise operations, such as XOR, shift, cyclic redundancy check,and the Hash operations, whereas readers and back-end servers are powerful devices that can perform complex cryptographic operations, such as running public key encryption algorithms.Communications between tags and readers are not secure because they communicate wirelessly and tags cannot support complex cryptographic operations.However, communications between the reader and server are secure because a secure channel is established before they communicate.

As the RFID technology has been widely used in commercial domains, the privacy issue caused by this technology has drawn considerable attention in recent years.For example, traditional low-cost tags provide no privacy when they authenticate an RFID reader because these tags broadcast their identities upon receiving a reader’s request and customer’s preferences and buying patterns are violated when attackers eavesdrop on the authentcation information.The Commission of the European Communities[1]issued recommendations on RFID-based applications, providing advice for protecting tag privacy and tag data security.

High-performance tags that support elliptic curve cryptography (ECC) were developed[2]-[8]to address the issue of tag privacy and other security problems.Furthermore, some RFID authentication protocols[9]-[18]based on ECC were proposed.However, few of these protocols have formally proven to provide tag privacy, and as stated by He and Zeadally[19], suitable security models are required to prove the security properties of the proposed schemes.

Herein, we propose a mutual authentication protocol that provides a fixed period of time for an RFID reader to identify a tag, and we also present a tag privacy model.Furthermore, we prove that the proposed protocol preserves privacy in our model and demonstrate that the proposed protocol performs the best under overall evaluations on tag privacy, tag computation cost, and communications cost.

The remainder of the paper is organized as follows.Section 2 introduces the related work, and Section 3 briefly describes the preliminaries.In Section 4, we describe the proposed protocol.We explain the tag privacy model in Section 5 and provide a security analysis of our protocol in Section 6.Section 7 provides comparisons between our protocol and other recently proposed protocols.Finally, Section 8 concludes the paper.

2.Related Work

In some RFID-based applications (e.g., E-passport, luxury goods management, and important access control systems) that require higher-level security, low-cost RFID tags that support simple operations, such as bitwise operations (XOR, AND, and Additive), shift operation, cyclic redundancy code, and pseudo-random number generator cannot guarantee sufficient security.With advances in the technology and reduction in costs, RFID tags[2]-[8]that support ECC were developed for applications that require high security.RFID authentication protocols based on public key cryptosystems are necessary for secure communications[20].

Recently, Liao and Hsiao[16]proposed an ECC-based RFID authentication protocol.However, it is inefficient because it requires five elliptic curve-point multiplication operations on the tag side.Zhao[21]also stated that Liao’s scheme suffers from the key compromise problem.Focusing on RFID implant systems, Moosaviet al.[17]designed a mutual authentication scheme based on ECC and the Hash function; however Khatwani and Rog[22]reported this scheme to be vulnerable to denial of service attacks and proposed an improved scheme against these types of attacks.Zhang and Qi[18]proposed an authentication protocol based on ECC for patient medication;however, Farashet al.[23]demonstrated that this scheme cannot provide forward privacy and improved this scheme by employing the Hash function.Heet al.[11]proposed an ECC-based authentication scheme and claimed that their scheme provided high security.However, Lee and Chien[15]reported that this scheme guarantees no privacy protection under active tracking attacks and proposed an improved version to overcome this flaw.Chen and Chou[10]proposed an ECC-based authentication protocol exhibiting untraceability and scalability for active tags and evidenced the privacy property.However, Shenet al.[24]demonstrated that this scheme cannot resist server spoofing and replaying attacks.

3.Preliminaries

In this section, we briefly introduce ECC and the decisional Diffie-Hellman (DDH) problem.

3.1.Brief lntroduction of ECC

ECC was first introduced by Koblitz[25]and Miller[26].Suppose that integersaandbdefine an elliptic curvey2=x3+ax+b, where 4a3+27b2≠0, and the points with coordinates (x,y) on the curve, including an infinite pointO, satisfy the equation.An addition operation of the points forms a cyclic additive groupG.Operations for the elements ofGare defined as follows: 1) If a pointP=(x,y) is an element ofG, then −P=(x,y) andP+(−P)=O;2) if two pointsPandQare different elements andP≠−Q, thenP+Qis defined as follows: If a lineLis drawn throughPandQ, thenLwould intersect with the curve and we define the intersection point by −RandP+Q=R;3) if a pointP=(x,0), thenP+P=O; otherwise, a tangent line is drawn throughP, and then the intersection point is denoted by −RandP+P=2P=Ris defined; 4) there exists a generatorPinGthat can generateG, namely,G={P,2P,…,(n−1)P,np=O}, where integernis the order ofG; 5) the operation of “+” satisfies the commutative and associative laws, namely,P+Q=Q+PandP+(Q+R)=(P+Q)+R, respectively.

3.2.Decisional Diffie-Hellman (DDH) Problem

When the ordernof a groupGis sufficiently large, given a generatorPofGand three random elementsP1=aP,P2=bP,P3=cP∈G(a,b,c∈are unknown), it is computationally infeasible to decide whetherab=cmodn.

4.Proposed Protocol

In this section, we propose a mutual authentication protocol based on the work introduced in Section 2.Our protocol achieves tag privacy preservation and scalability and resists attacks such as the man-in-the-middle attack,replay attack, reader/tag impersonation attack, and desynchronization attack.

4.1.Symbols

For readability, the symbols used herein are listed in Table 1.

Table 1:Symbols

4.2.Proposed Protocol

The proposed protocol is shown in Fig.1.It can be interpreted as follows.

1) First, readerRfirst generates a random numbera∈Rand it then computesM1=aP∈Gand sendsM1to tagT, whose identifier isti.

2) Upon receivingM1,Tgenerates another nonceb∈Rand it then computesM2=bP,K1=bM1,K=K1+bY,m3=ti+H(M1,M2,K1,K), andm4=H(M2,K,ti), whereM2,K1,K∈G.Finally,Tresponds toRwithM2,m3, andm4.

4) Upon receivingm5,Tverifies whetherm5=H(M1,M2,K,ti) If it is true, thenTupdates its identifierti=[H(ti,K)]ℓT.Otherwise,Tfails in authenticatingR.

Fig.1.Description of the protocol.

5.Tag Privacy Model

In this section, we describe a tag privacy model that defines the tag forward privacy and backward privacy.

We provide a probabilistic polynomial time (PPT)adversaryAwith the following oracles to simulate its abilities to launch protocols, observe authentication results, impersonate a reader/tag and send a message to a reader/tag in a session, and corrupt tags.

1) Authenticate(R,T): This oracle is provided forAto launch an authentication session betweenRandT.IfAknows the secret information ofRandT, then the session transcripts, secret information ofRandT, and the authentication result are returned toA.Otherwise, only the authentication result and session transcripts are returned.

2) Observe(R,T): It makesRlaunch an authentication session withTand return the session transcripts as well as the authentication result.

3) Corrupt(T): It is provided forAto corrupt tagTand return the secret information ofT.

4) Send(T/R,m): This oracle sends the messagemtoT/R, which is involved in a running session, and returns the response based on the protocol’s specification.IfT/Ris not involved in a running session, this oracle launches a new authentication session and sendsmtoT/R, and it then returns the response based on the specification of the protocol.

5) Test(T): It is provided for adversaries only once at any given time.This oracle launches an authentication session betweenRandTand completes this session, and then selects a random bitb∈R{0,1}.Ifb=1, the transcript of the authentication session is returned; otherwise, a random transcript that has the same format as that of a true authentication session transcript is returned.

For readability, we denote the first four oracles byO.Informally, the tag forward privacy implies that a PPT adversaryAcannot distinguish the subsequent activities of a target tagTeven if the secret information within the tag is disclosed, and the tag backward privacy implies thatAcannot distinguish the previous activities ofTeven if its secret information is disclosed.Based on challenge games, we defined the tag forward privacy and backward privacy as follows.

Definition 1.ChallengerCprovides the private key ofRtoA, andAcan query oracles inO.At a given time point,Aselects a corrupted tagfor queryingThereafter, it can continue to query oracles inOeven with permission to query Authenticatewherek≥1.Finally,Aprovides a bitb′∈{0,1} to end this game.

6.Security Analysis

Moreover, our protocol provides forward privacy and backward privacy and satisfies other common security properties.We provide proofs in the following subsection.

6.1.Forward Privacy and Backward Privacy

We now demonstrate that if a PPT adversaryAcan break the forward privacy and backward privacy of our protocol, then we can construct an algorithm to solve the DDH problem.

Theorem 1.For any PPT adversaryA, the proposed authentication protocol provides forward privacy according to Definition 1.

Proof.ChallengerCinitializes the system parametersGF(q),n,G,P, and the private and public key pairy,Y=yPfor a readerR.Calso initializes each tagTwith(i= 1, 2, ···,nT) and the database ofRwith(i= 1, 2, ···,nT) and provides the private keyytoA.CselectsP1=aP,P2=bP, andP3=cPfromG, wherea,b,andcare unknown.The goal ofCis to determine whetherabP=cPis true.We guessAwill select tag∈(1,2,…,nS) as its target tag.

AsCpossesses the private keyyand the identifier of each tag,Ccan simulateRand each tag and interact withAas follows.

6.2.Common Security Properties

A.Resistance to Man-in-the-Middle Attack

When the protocol is running, an attackerAcan intercept the first round of message (M1) and replace it with another messageand sendto tagT.Upon receivingToperates based on the protocol’s specification and responds with the second round of message (M2,m3,m4) to the reader.

WhenAinterceptsM2,m3, andm4, it may replace them withrespectively; however,m3is the value of the tag’s secret identifiertiplus a Hash value related toM1, andm4is a Hash value related totiandK(which is also related toM1).In other words,should be computed with the first messageM1to pass the verification ofR.Hence,Acannot successfully launch a man-in-the-middle attack.Moreover,Acannot correctly generatem3andm4to pass the reader’s verification without knowingti, except in the case of a negligible probability.

B.Resistance to Replay Attack

The authentication sessions of our protocol are initiated by the reader, and our protocol employs secret noncesa,b, and the evolution identifiertito compute the exchanged messagesM1,M2,m3,m4, andm5.Hence, attackers cannot replay these messages to the reader/tag to pass the verification.

C.Resistance to Reader Impersonation Attack

The reader in our protocol employs the private keyyto compute the temporary keyK, and the last round messagem5is a Hash value that is related toKand tag’s identifierti.Hence, attackers cannot impersonate the reader without the knowledge ofyandti, except in the case of a negligible probability.

D.Resistance to Tag Impersonation Attack

The tag in our protocol uses its identifiertito computem3andm4, and adversaries cannot impersonate the tag without possessingtito pass the reader’s verification, except in the case of a negligible probability.

E.Resistance to Desynchronization Attack

To desynchronize the reader and tag,Amay block the last round messagem5to prevent the tag from updating its identifier when an authentication protocol is running.However, the reader can recover synchronization with its tag in the next session using an old identifierwhich is the last successful synchronization identifier between the reader and tag.

7.Comparisons with Related Work

We compared our protocol with some recently proposed protocols that are based on ECC.The comparisons focus on tag privacy preservation and performance.The conclusions drawn from the comparisons of scalability (S1), mutual authentication(S2), forward-privacy preservation (S3), and backwardprivacy preservation (S4) are summarized in Table 2.Table 3 lists the computation and communications costs for comparisons.

7.1.Comparisons of Privacy Properties

Results listed in Table 2 show that our protocol and that proposed in [15] provide both tag forward and backward privacy.The results can be explained as follows.

1) All the ECC-based schemes provide a fixed period of time for the reader to identify a tag and provide mutual authentication between the reader and tag.

2) The schemes proposed in [16] and [11] do not provide forward and backward privacy based on the analysis of [27] and [15], respectively, and those proposed in [18] and [21] do not forward privacy based on the analysis of [23].

3) Under our tag privacy model wherein an attackerAcan obtain a reader’s private key, the scheme proposed in [18] does not provide backward privacy becauseAcan easily determine the identifier of the target tag once it receives the authentication transcripts.The schemes proposed in [4] and [23] do not provide forward and backward privacy because the identifiers of the tag are constant in these schemes, andAcan easily determine the Hash value of the identifier of the target tag if it receives the transcripts of authentication sessions.

7.2.Comparisons of Computation and Communications Costs

As readers/servers are known to be powerful devices, we analyzed the computation cost on the tag side andthe protocol communications cost.We denote the running time of a modular multiplication operation byTmm, a point addition operation over an elliptic curve byTeca, a scalar multiplication operation over an elliptic curve byTecm, and a Hash operation byTha.In terms of the work by Chatterjeeet al.[28], we have the proportion thatTeca≈ 5Tmm,Tecm≈ 1 200Tmm, andTha≈ 0.36Tmm.To sum up the protocol communications cost, an elliptic curve is assumed to be defined in a finite fieldF(2160), which needs 40 bytes to store an elliptic curve point and 20 bytes to store an element of the field.We employ the Hash scheme[29]as our Hash function whose output length is 10 bytes.The comparison results are listed in Table 3.

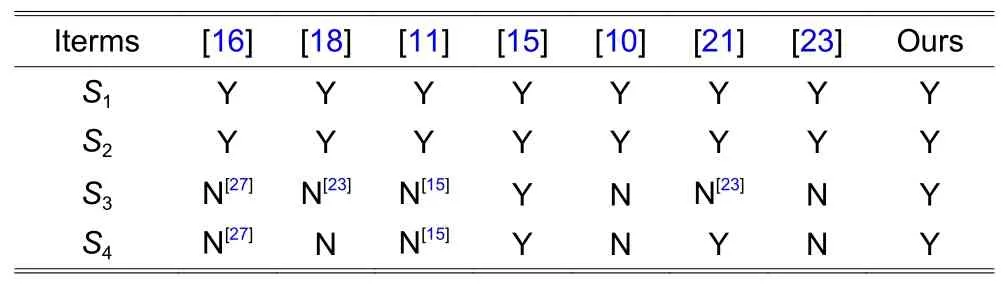
Table 2:Comparisons of privacy properties

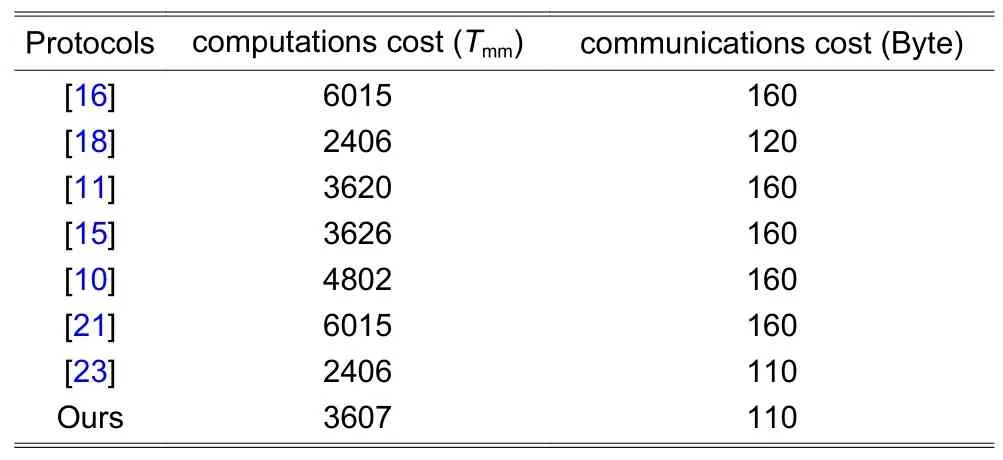
Table 3:Comparisons of computations and communications costs

The comparison in Table 3 shows that the protocols proposed in [20] and [27] have the highest computation cost on the tag side (6015Tmm), whereas those in [9] and [26] have the least computation cost (2406Tmm).The computation cost of our protocol is in the range of intermediate-high values (3607Tmm).

With regard to the communications cost, the results listed in Table 3 show that our protocol and that in [9] have the least communications cost (110 bytes), whereas the other protocols spend more on communications(≥120 bytes).

8.Conclusions

We proposed an ECC-based RFID authentication protocol, which takes a fixed period of time for a reader to identify a tag and provides a mutual authentication between the reader and tag.Furthermore, we proposed a tag privacy model wherein adversaries can receive the reader’s private key corrupt tags, launch and eavesdrop on protocol sessions, and send messages to readers/tags.Using this model, we formally proved the privacy property of the proposed protocol.We also demonstrated that our protocol meets the general security requirements such as resistance to replay, man-in-the-middle, impersonation, and desynchronization attacks.Analyses showed that our protocol performs better compared with the other schemes and can be used in applications that require high privacy and security.

Disclosures

The authors declare no conflicts of interest.