让“经历”变成“经验”

桑坤

摘要：解决“草坪面积问题”时，学生存在不假思索地把四段小路拼起来的情况。这是因为产生了负迁移。负迁移的出现缘于学生对既有方法理解的模糊，以及缺乏动手实践、自主探究的实质性活动经验。对此，应带领学生经历探究过程，以达成对方法的深度理解。具体实施时，可借助多元表征，促进迁移的“正向”生长;通过做思共生，促进数学活动经验的“正向”积累，让“经历”变成“经验”。

关键词：小学数学;草坪面积问题;负迁移;多元表征;做思共生

一、案例描述：用常规思路却出错了

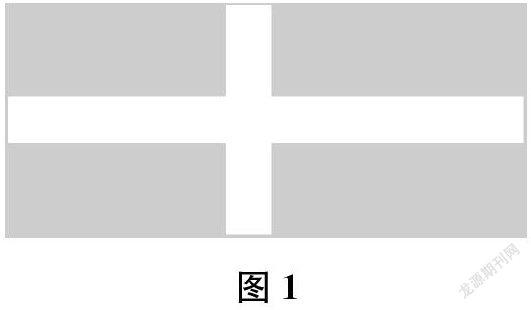
在学习五年级上学期“多边形的面积”相关内容后，学生在练习中碰到这样一道题：“如图1所示（为便于示意，草坪比例有调整），有一个长60米，宽24米的长方形草坪，王叔叔在草坪中设计了两条宽为2米的小路。这个草坪的面积是多少平方米？”

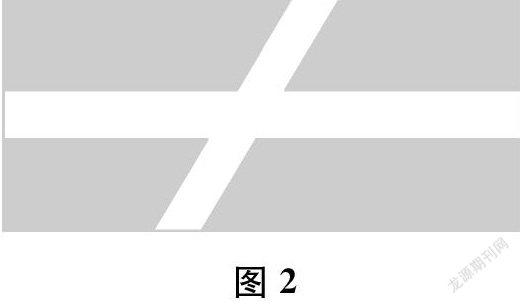
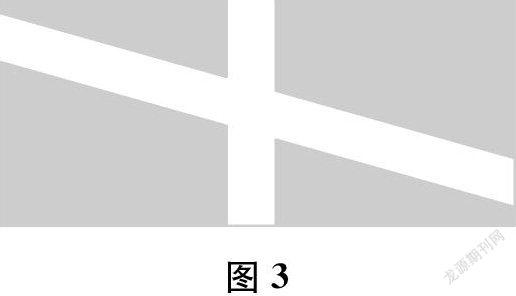
学生通常会通过剪、拼，将四块小草坪拼成一个长方形，从而算出草坪的面积。即长为60-2=58（米），宽为24-2=22（米），草坪面积为58×22=1276（平方米）。这种方法对于解决这道题是完全可行的。但这样做为什么可行？很多教师并未作出详细的解释。当把题目中小路的位置进行相应的调整（如图2和下页图3所示）后，学生会借助原有的知识经验，不假思索地把四段小路拼起来，算出草坪的面积。

但如果继续调整小路的位置（如图4），还可以用上面的方法去解决吗？答案是否定的。如果继续沿用，算出的草坪面积将是错误的。

二、案例分析：缺乏本质理解，导致负迁移

新的学习往往以原有的学习为基础， 原有的学习经历可能对后续的学习产生促进效果， 也可能产生阻碍作用。后者在心理学上被称为“负迁移”。当草坪中的两条小路分别平行于长方形的长和宽时，通过剪、拼，能够将四块小草坪拼成一个新的长方形;当两条小路中只有一条小路平行于长方形的长或宽时，也可以通过剪、拼，将四块小草坪拼成一个新的长方形。在一系列相关知识的建构过程中，“只要草坪中有小路，都可以通过剪、拼，将四块小草坪拼成一个新的长方形”的认知逐渐在学生的头脑中形成。因此，在解决变式题目时，学生在没有真正理解这一内容的内涵及本质的情况下，仅仅根据自身的已有知识经验，极易被表面的相似迷惑。这是基于不成熟的数学认知的不恰当的迁移，即产生了负迁移。

负迁移的出现缘于学生对既有方法的模糊理解，以及缺乏动手实践和自主探究的实质性活动经验。当题目发生改变，即草坪中的两条小路都不平行于长方形的长与宽时，学生仅依靠对类似题目的模糊“经历”，用理解不够深刻的方法去解决，导致了错误的发生。

三、改进后的教学

（一）自主探究，验证猜想

师（出示图1）像王叔叔一样，在长60米，宽24米的长方形草坪中自主设计两条笔直的小路，小路的宽度还是2米，把你的设计画出来。

（学生完成设计。）

师刚刚老师拍了一些同学的作品，（出示学生作品）你們能帮老师分分类吗？同桌交流，互相说一说你的分类方法和理由。

（学生交流汇报。）

生可以分成三类，第一类和原题一样，两条小路分别平行于长方形的长和宽。

师是的，我们可以分成三类。第一类是两条分别平行的。（板书：两条分别平行）那第二类呢？

生只有一条小路平行于长方形的边。

师是的，只有一条小路平行于长方形的边，这条小路平行于长或者平行于宽。我们记作只有一条平行。（板书：只有一条平行）那第三类呢？

生两条小路都不平行于长方形的边。

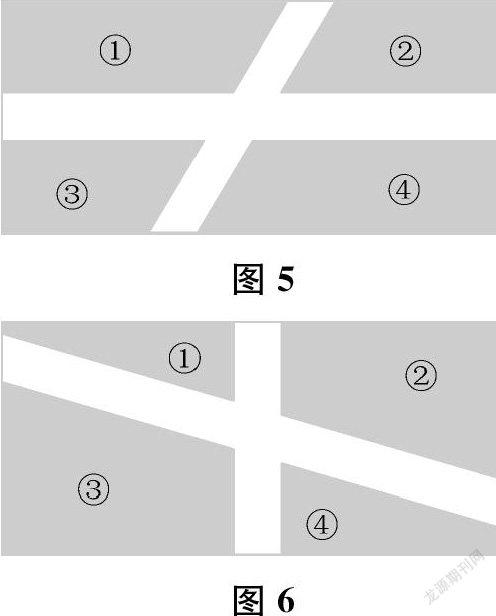
师我们记作两条都不平行（板书：两条都不平行）。第一类两条分别平行的情况，之前已经通过动画进行了验证。接下来，我们重点研究第二类和第三类。先来看第二类，（出示图5、图6）这些草坪去掉两条小路后，剩余部分都能拼成一个长方形吗？

生能。

生不能。

师看来大家有争议，口说无凭，让我们一起来验证，请大家完成学习单的第一部分。活动要求为：（1）打开1号文件夹，同桌两人合作选择一种方案剪一剪、拼一拼，注意保留完整的小路;（2）把剪好的四块“草坪”贴在各自的磁铁板上，动手操作，检验是否能够拼成长方形;（3）在小组中交流作品，记录你的发现，准备汇报，贴磁铁板汇报时注意先还原再演示。我们可以这样汇报：“我选择的是方案（），通过操作我发现，（能、不能）拼成长方形。”

（学生完成操作活动，指定小组汇报。）

师通过刚才的操作，我们发现，当一条小路平行于长方形的边时，确实能通过剪、拼得到一个新的长方形。那同学们想过没有，为什么第二类情况下，去掉小路后剩余的四块“草坪”还可以拼成长方形？

（学生回答。）

师（出示图7）只有一条小路平行于长方形的边时，两条小路可以看成由三个平行四边形和两个梯形组成，平行四边形的对边平行且相等，所以去掉小路后剩余的四块“草坪”可以拼成一个长方形。

师刚刚我们已经验证了前两类，（出示图8、图9）那第三类我们是不是可以不用验证直接下结论了？

生不能。

师该怎么办？

生继续验证。

师我们继续来动手验证。请打开2号文件夹，按照相同的活动要求完成第三类的验证。

（学生完成动手操作验证活动。）

生当两条小路都不平行于长方形的边时，不能拼成一个长方形。

师为什么第三类不可以通过剪、拼，将剩余部分拼成长方形呢？

（学生回答。）

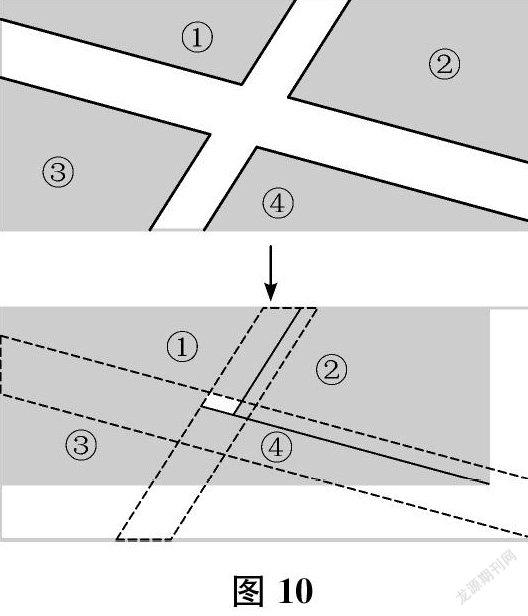
师（小结验证方法，如图10所示）当两条小路都不平行于长方形的边时，这两条小路可以看作是由四个梯形和一个平行四边形共同组成的。当把四块“草坪”拼在一起时，实质上就是将梯形的两个底拼接，但由于梯形的两底不相等，在外边沿对齐的情况下，就形成了中间部分还空出一块的结果。这说明，当两条小路都不平行于长方形的边时，四块“草坪”无法转化成一个完整的长方形。

（二）自主建构，思维进阶

师同学们，当我们遇到新的问题并且有一些想法时，我们要做的就是大胆地去验证这些猜想。通过刚才的验证，你知道了什么？

生至少有一条小路平行于长方形的边时，可以拼成长方形;两条都不平行时，就不能拼成长方形。

师说得真好！同学们，刚刚我们先有了猜想，然后又对猜想进行了验证，最后我们得出了结论。猜想有可能是正确的，也有可能是错误的。正确与否，需要进行验证，我们要用科学的态度来研究数学问题，正如荷兰数学教育家弗赖登塔尔所说：“真正的数学家常常凭借数学的直觉思维作出各种猜想，然后加以证实。”其实你们每个人都是小小数学家，只要你们勇于探究，就会发现更多数学中的学问。

四、相关思考：“正向”，才能让“经历”变成“经验”

（一）借助多元表征，促进迁移的“正向”生长

研究表明，在教学较难理解的内容时，可以通过多元表征减轻学生理解知识的负荷。要让学生真正地将对数学知识的理解内化于心，并且能够重新建构对知识的认知，不仅要丰富知识的不同表征形式，而且要在不同的表征形式间建立联系，从而真正地丰富对知识的理解。如果将定义描述为“骨架”，不同表征便是“血肉”，它们之间有了联系，就能真正达成理解，也就有了“灵魂”，正迁移在此过程中自然发生。

在探究草坪中的小路（情境）的相关内容时，学生可以借助原有的知识，知道可以把四块小草坪拼起来，完成自我建构。在表达时，通过画图（图像）将自己的想法展示给其他同学，在合作交流（语言）的过程中，达成共识。接下来，进一步合作交流，明确有三种不同的情况，继而通过对三种情况的分类探究，发现横竖都不平行的情况是无解的。在回顾反思中，对这几种情况进行知识的重新建构，明确“至少有一条小路平行于长方形的边时，可以拼成长方形;两条都不平行时，就不能拼成长方形”。通过情境、图表、语言等多元表征，学生在探究性的活动中，把对难点的理解暴露出来，进而通过经历尝试、猜想、验证、再猜想、再验证、归纳等过程，探究出知识的本质，削弱负迁移对学生的固有影响，促进迁移的正向生长。

（二）通过做思共生，促进数学活动经验的“正向”积累

教育家苏霍姆林斯基说过：“儿童的智慧在他的指尖上。”动手操作是学生学习数学知识的重要途径和基本方法。但“做”不是目的，“做思共生”才是动手操作活动的旨归。

改进后的《草坪面积问题》一课，精心设计了3次动手操作活动。在这3次动手操作活动中，教师通过安排合理的学习材料，组织合理的学习活动，给学生充足的自主探究时间，促使学生积累研究活动的直接经验，带着这样的经验走入小组，分享收获、解释发现和方法、阐明观点、经历修正和完善，在达成学习共同体的构建过程中，不断提升自我学习力。在深入探究的过程中，动手操作和深度思考讓“经历”变成“经验”。

参考文献：

[1] 贲友林.关于获得数学活动经验的三点认识[J].江苏教育，2011（34）.

[2] 王倩.用儿童的方式抵达数学的内核——苏教版教材 “动手做”价值分析与实施路径[J].小学数学教育，2019（1/2）.

[3] 何健.思维可视化：提升学生的逻辑推理力[J].数学教学通讯，2020（10）.