钨中空位及其团簇的能量学和动力学性质参数
2021-01-21孔祥山刘长松
孔祥山,刘长松
(1.山东大学 材料科学与工程学院,山东 济南 250061;2.中国科学院 固体物理研究所,安徽 合肥 230031)
钨(W)基材料以其高熔点、高热导率、与氢同位素化学亲和性低以及低溅射率等性能被视为未来聚变堆面向等离子体材料(PFM)的最佳候选材料[1-2]。作为PFM,W将遭受高能、高通量的聚变中子辐照。这将在W中引入大量缺陷。空位及其团簇便是其中1种主要缺陷,它们影响并决定着W中微观组织结构和氢同位素滞留性质,最终影响和改变材料的力、热性能[3]。空位及其团簇的能量学和动力学行为已被广泛研究[4-54]。尽管如此,空位及其团簇的能量学和动力学基本性质参数仍不完整且存在一些争议[4-54]。本文将对文献中现有的空位及其团簇的能量学和动力学性质参数进行总结,并采用第一性原理(FP)方法计算获得更加完整和精确的基本性质参数,并探讨文献中相关争议的可能原因。
1 计算方法
本文采用VASP软件来开展FP计算[55-56]。所有FP计算均采用缀加投影波方法(PAW)描述电子波函数[57],采用局域密度近似(LDA)[58]和广义梯度近似(GGA)来描述电子的交换关联泛函,其中GGA包含PW91[59]、PBE[60]、PBEsol[61]和AM05[624种形式。电子波函数用平面波展开,能量收敛程度主要取决于平面波截断能和第一布里渊区k点的取样密度。本文采用500 eV 的平面波截断能和3×3×3的k点网格,总能量收敛优于0.1 meV/atom。计算采用4×4×4的超胞(含250个晶格格点)。结构优化截止条件为原子受力小于0.01 eV/Å(1 Å=10-10m)。扩散性质计算采用cNEB方法[63]。
单空位V1形成能计算公式:
(1)

空位团簇Vn结合能计算公式:
(2)
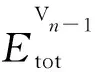
2 结果和讨论
2.1 体心立方钨基本性质参数
图1 示出了体心立方W基本性质参数,包括晶格常数、体弹模量和内聚能。由于采用的交换关联函数、截断能、K点、晶胞大小等不同,W基本性质参数FP计算结果具有一定偏差。晶格常数FP计算结果偏差较小(3.125~3.18 Å,变化范围小于0.06 Å),与实验值3.163 Å[64]基本一致。其中,采用LDA计算得到的晶格常数略低于实验值,而GGA-PBE和GGA-PW91计算结果略高于实验值。对于体弹模量,不同文献报道的FP计算结果间存在较大差异(294~344 GPa),受交换关联函数影响较大。本文采用大超胞和高截断能(250格点、500 eV)计算获得了与实验值(312~314 GPa)一致的理论值(313~318 GPa),且计算结果表明受交换关联函数影响较小。对于内聚能,FP计算结果变化范围为8.39~11.81 eV。与实验值(8.66 eV和8.9 eV)相比,LDA显著高估了内聚能,GGA略微低估了内聚能。在W基本性质参数方面,GGA明显优于LDA,其中PBEsol、AM05和PBE又略微优于PW91。图1中还示出了基于已开发的十几种W经验势计算得到的基本性质参数,与实验结果具有较好的一致性。这说明这些势函数都能较好地描述上述W基本性质。
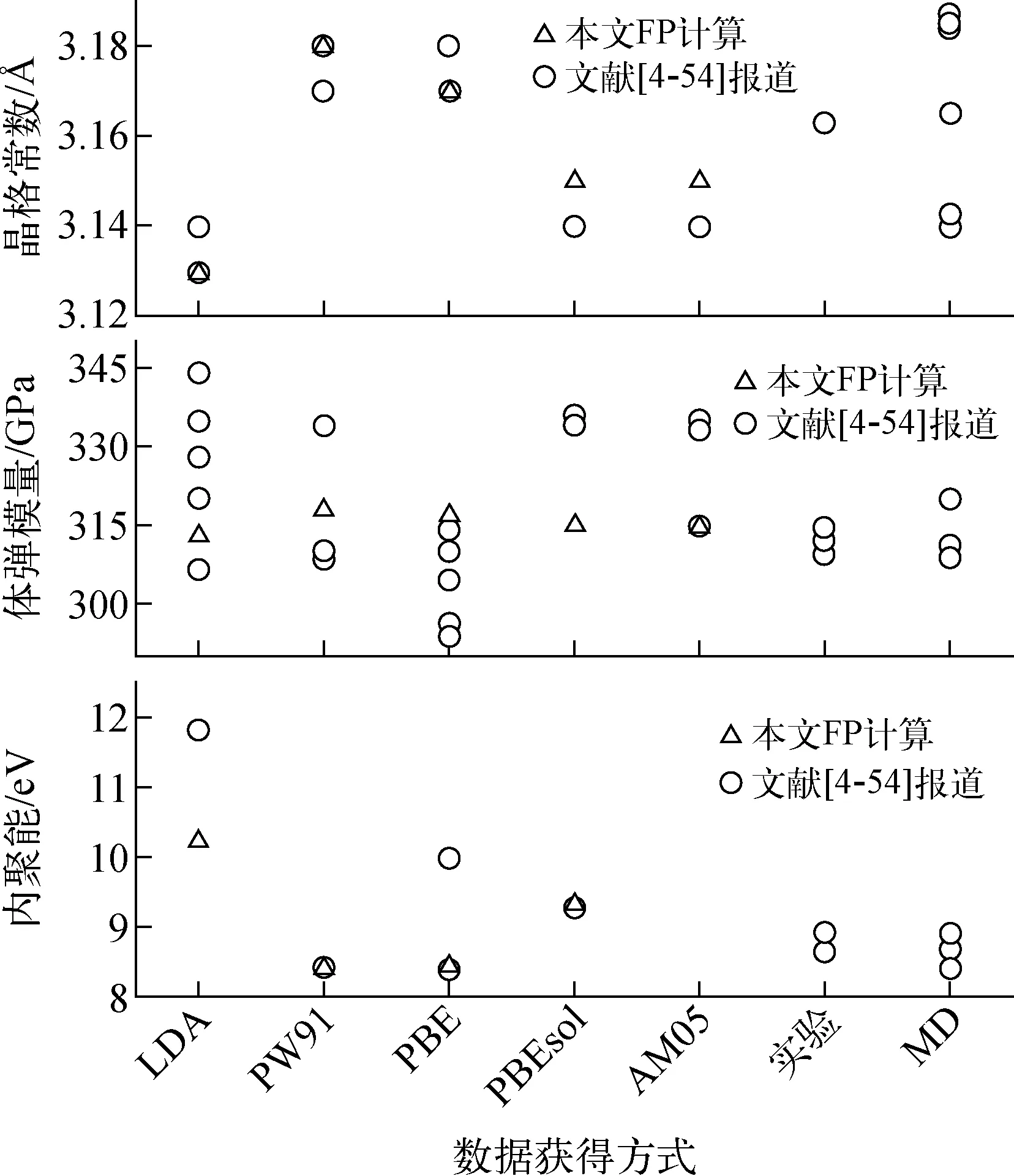
图1 W基本性质参数Fig.1 Basic property parameter of tungsten
2.2 单空位形成能和扩散能垒
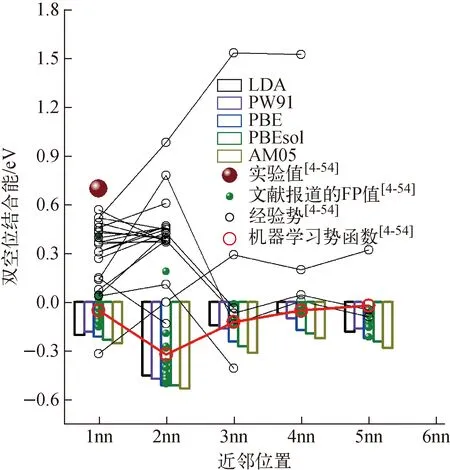
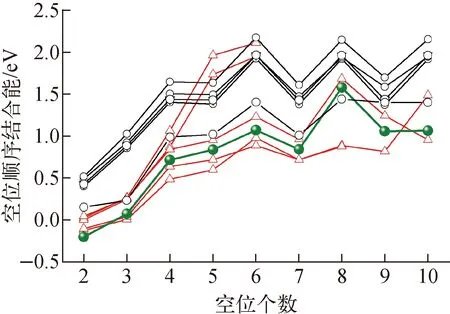
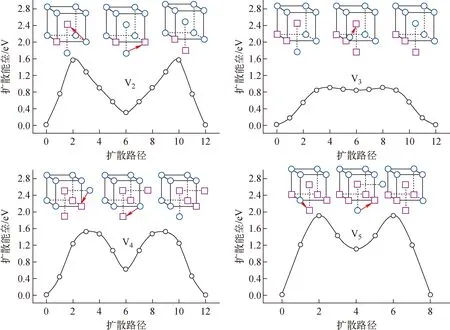
图2a为空位形成能FP计算结果和实验结果。由图2a可知,不同交换关联函数的计算结果相差较大,表明空位形成能对交换关联函数十分敏感。采用PW91计算得到空位形成能较采用AM05得到的计算值小0.4 eV。除个别FP计算外,空位形成能FP计算值随交换关联泛函的变化遵循PW91 红色三角形为本文FP计算数据;蓝色五角星为热膨胀和电子熵修正后的空位形成能;空心圆圈为文献[4-54]报道的数据图2 W中单空位形成能和扩散能垒Fig.2 Formation energy and diffusion energy barrier of single vacancy in tungsten 本文还采用PBE和PW91计算了单空位扩散能垒。如图2b所示,本文结果与文献报道的结果具有很好的一致性。PW91、PBE、PBEsol和AM05,这些GGA泛函所得扩散能垒差异较小(1.65~1.85 eV),略低于LDA(1.95 eV)。这表明单空位扩散能垒FP计算对交换关联泛函不敏感。实验上无法直接获得扩散能垒,而是利用通过Arrhenius方程拟合空位扩散系数得到的空位扩散激活能减去空位形成能得到。然而,到目前为止,W中单空位扩散系数尚无准确实验测量数据,仅获得了高温下的W自扩散系数。对W自扩散系数采用双Arrhenius方程拟合,获得较小的扩散激活能常被认为对应W的单空位扩散,其值约为5.6 eV[67]。此处,本文将FP计算得到的空位扩散能垒与经晶格热膨胀和电子熵修正后的空位形成能相加获得空位激活能,LDA、PW91、PBE、PBEsol和AM05计算所得单空位扩散激活能分别约为5.95、5.58、5.74、6.04和6.18 eV。其中,PW91和PBE结果与实验测量值接近,而LDA、PBE和PBEsol均大于实验测量值。因此,认为PW91和PBE可能更适合用于研究W中空位的热力学和动力学性质。 图2还示出了采用W经验势函数计算得到的空位形成能(分布在3.28~3.82 eV范围内)和扩散能垒(分布在1.2~2.2 eV),部分经验势结果与实验测量值以及FP计算值相近,表明它们可用于研究W单空位的能量学和动力学行为。本文仍需指出由于W中单空位形成能实验测量值间存在很大偏差以及单空位扩散系数无法测量,到目前为止仍不能确定上述哪种方法计算得到的空位性质是绝对准确可靠的,还有待于进一步的实验和理论研究。 W中空位相互作用已被广泛研究,然而对于双空位相互作用性质目前仍存在很大争论。W中双空位结合能示于图3。图3中,正值表示双空位相互排斥,负值表示双空位相互吸引。实验值、文献报道的FP值、经验势、机器学习势函数的值来源于文献[4-54]。由图3可知,大部分FP计算得到的双空位结合能均为负值,这表明W中双空位相互作用以排斥为主。具体来说,双空位位于第2近邻(2nn)时排斥作用最为强烈,其他近邻位置排斥作用较为微弱。部分FP计算结果表明双空位位于第1近邻(1nn)时具有微弱的吸引作用。双空位结合能FP结果间的差异主要是与不同FP计算采用的超胞、截断能以及FP程序包有关。其中,PLATO(linear combination of atomic type orbitals)程序包计算得到第1近邻和第2近邻双空位结合能分别为0.41 eV和0.19 eV,即双空位相互作用为吸引[5]。该结果与其他FP程序包计算结果具有显著差异。本文利用VASP程序包采用5种交换泛函系统计算了双空位结合能。如图3所示,本文结果与大部分FP计算结果具有较好的一致性,双空位在第2近邻处具有最强的排斥作用(结合能约为0.4 eV)。此外,从图3还可看出,采用不同交换关联函数计算得到的双空位结合能差异较小(小于0.15 eV),表明交换关联函数对双空位结合能的影响较小。 图3 W中双空位结合能Fig.3 Binding energy between double vacancies in tungsten 与大量的FP研究不同,目前仅Park等在20世纪80年代利用场离子显微镜和测量电阻率的方法研究了高温淬火W中双空位行为,并推导出双空位结合能为0.7 eV[6]。这意味着W中双空位相互作用性质为吸引。实验结果与FP的巨大差异可能来源于:1) 温度效应,实验考察的对象是高温区间的双空位结合行为,而FP计算结果对应着绝对零度下的双空位结合行为,晶格热膨胀可能会影响甚至改变双空位的结合性质;2) 杂质效应,近期理论计算表明杂质能促进空位的结合,将双空位间相互作用性质由排斥转变为吸引,而双空位与杂质间的结合作用十分强烈(双空位对碳的捕获能约3.5 eV),实验中很难排除这些杂质的影响[7]。 图4为W中空位团簇(Vn,n<10)结合能随其所含空位个数变化的FP计算结果。本文FP计算所得结果与文献报道的FP结果在V2与V3处具有较好的一致性,但随着空位团簇的增大,彼此间的差异也在变大(<0.5 eV),其原因是不同文献所采用的FP计算参数(晶胞尺寸、截断能、交换关联泛函、程序包等)和团簇构型存在一定差异。尽管在绝对数值上存在一定差异,但不同FP计算所得空位团簇结合能随所含空位个数的变化趋势基本一致。除V2与V3具有弱相互作用外,大空位团簇(n>4)对单空位具有非常强的捕获作用。空位团簇结合能随着所含空位个数增多呈现波动性增大的趋势,表明捕获作用逐渐增强。V2与V3的弱相互作用将导致纯W中空位团簇聚集成核只能发生在高空位浓度下。这是因为在低空位浓度下,多个空位同时聚集在一起形成空位数大于4的稳定空位团簇的可能性较低。 绿色小球为本文采用PBE交换关联泛函的计算结果,红色三角和黑色圆圈分别为文献报道的FP值和分子动力学计算结果[4-54]图4 空位团簇结合能Fig.4 Binding energy of vacancy cluster V2具有排斥作用,V3具弱吸引作用,但它们在一定温度下仍有可能稳定存在,这主要取决于它们的解离能。为此,本文进一步计算了空位团簇V2、V3、V4和V5中的空位与其近邻W原子间的扩散能垒(图5)。由图5可知,V2中空位与近邻W原子扩散能垒为1.6 eV,即构型由第1近邻转变为第2近邻。如此高的扩散能垒可有效阻碍双空位的解离。由此可推测在低温下(约<600 K)双空位一旦形成便能稳定存在。对于V3,近邻格点的W原子可跃迁到近邻四面体间隙位置,团簇结构由V3转变为V4与四面体间隙W原子相结合的复杂结构,其扩散能垒为0.8 eV,远低于单空位扩散能垒。这一较低的扩散能垒表明V3的稳定性较低,极易解离。对于V4和V5,空位与其近邻格点的扩散能垒分别为1.6 eV 和1.8 eV,表明V4和V5能稳定存在。 图5 V2、V3、V4和V5空位团簇中的空位与其近邻W原子间的扩散能垒Fig.5 Exchange energy barriers between vacancy and its neighboring W atom in V2, V3, V4 and V5 除FP计算外,人们还采用经验势函数计算了空位团簇的结合能。文献报道的结果总结在图3和图4中。从图3可看出,大部分经验势函数预测W双空位间存在较强的吸引作用,与实验结果相近,但与FP预测结果相反。此外,目前开发的传统经验势函数均不能很好地重现FP计算所得双空位结合能随距离的变化趋势(图3)。经验势与FP间的差异部分原因是上述W经验势函数多采用嵌入原子势(EAM),而EAM往往会低估表面能,进而导致高估了空位团簇结合作用(图4)。为此,Mason等[8]对EAM势进行了修正。修正后的EAM势预测双空位在第1近邻处为弱吸引,在第2近邻处为弱排斥,与FP结果具有较好的一致性。相比于其他势函数,该修正后的EAM势预测的空位团簇结合能与FP结果也更为接近。此外,Mason等还采用修正后的EAM势函数计算了V2和V3空位团簇中的空位与其近邻W原子间的扩散能垒,分别约为1.63 eV和1.59 eV。V3的结果与本文的FP结果存在较大差异。这是因为修正后的EAM势无法预测出V3向V4与四面体间隙W原子相结合的复杂结构的转变(图5)。近期,Byggmästar等使用高斯近似势框架开发了一种机器学习的W原子势函数(图3红色线)[9]。该势函数能很好地再现双空位结合能的FP结果。 (3) 本文采用FP计算方法系统研究了W基本性质(晶格常数、体模量、内聚能)和空位及其团簇的热力学和动力学性质参数(结合能、扩散能垒),并对现有文献数据进行了总结,对部分争议问题进行了分析和讨论。研究发现FP计算W基本性质参数方面,GGA明显优于LDA,其中PBEsol、AM05、PBE又略微优于PW91。FP计算的空位形成能低于实验测量值。从晶格热膨胀和电子熵贡献讨论了理论和实验间差异的原因,并基于此认为PW91和PBE可能更适合用于研究W中空位的热力学和动力学性质。空位扩散能垒对FP所用交换关联泛函不敏感。绝对零度下W双空位间以排斥作用为主,实验测量得到的双空位吸引作用可能受到晶格热膨胀或杂质的影响。空位团簇V3相互作用为弱结合,且其空位与近邻W原子间扩散能垒仅为0.8 eV,表明V3的稳定性较低,极易解离。Vn(n>4)对单空位具有非常强的吸引作用,其结合能随着所含空位个数增多呈现波动性增大的趋势。空位团簇稳定结构可通过最小化Wigner-Seitz表面积来确定,结合能与Vn与Vn-1之间的Wigner-Seitz面积之差呈正比。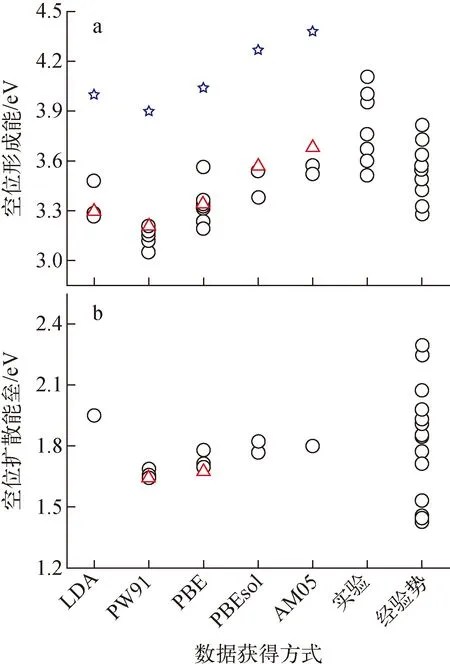
2.3 空位团簇能量学和动力学性质参数
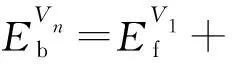
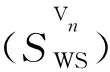
3 结论
