基于最小二乘的线性源特征线方法研究

陈 莹，梁 亮，张 乾，赵 强

(哈尔滨工程大学 核安全与仿真技术国防重点学科实验室，黑龙江 哈尔滨 150001)

随着反应堆物理计算精度要求的提高，基于特征线方法(MOC)的中子输运方法得到迅速发展。该方法是对中子输运方程的微分形式沿中子飞行轨迹进行积分的一种求解方法。理论上，该方法可求解任意复杂的几何输运问题[1]。近年来，国内外的一些组件计算程序，如CASMO[2]、DRAGON[3]、WIMS[4]等，一步法堆芯计算程序，如CRX-3D[5]、DeCART[6]、nTRACER[7]、MPACT[8]、NECP-X[9]等，均使用了特征线方法作为输运求解模块。除能量、时间和空间变量离散外，在特征线方法中，平源近似是重要的基本假设，即同一网格内源项相同。平源近似下，精确的计算结果需要较小的网格划分和较小的特征线线宽。因此平源近似需要的网格数量较大，导致几何信息和相关物理量的存储空间较大，影响了总的计算效率。

为改进平源近似带来的问题，Santandrea等[10]尝试将源项采用线性表示。线性源是将中子输运方程的右端项由常量替换为线性表达式。与平源近似相比，线性源可在较大网格划分时得到良好的计算结果。

Petkov等[11]在MARIKO程序中使用线性源特征线方法。Santandrea等[12]提出正定的表面特征线格式及改进的非线性表面特征线格式的线性源方法。由于该方法的非线性导致很多加速方法无法使用，Le Tellier等[13]提出一种简化线性特征线格式线性源方法，虽然这种计算方式在计算过程中使用了线性函数表示源项，但它未将通量表示为线性函数。汤春桃[14]在PEACH程序中采用坐标投影线性源方法计算源项斜率，并提出将源项在x、y方向投影的斜率计算公式，该方法的通量同样是平通量假设，因此对计算精度的提高有限。Chai等[15]提出的线性源方法列出每条特征线起始点、中点和终点3点的平衡方程，得到表示源和通量的斜率系数的计算方式，并开发了三维线性源特征线方法程序TCM_L，该方法给出的是三维几何模型的测试结果。Rodolfo等[16]提出一种线性源方法并应用在CASMO5中，该方法在使用线性函数表示源项的同时对通量也使用线性假设，因而理论上其对计算使用的网格数量不敏感，即使在大网格条件下也可得到精确的计算结果，但该方法在计算带气隙问题时需引入近似处理。朱成林[17]基于坐标投影线性源方法使用Dragon程序实现了坐标投影线性源方法在三维上的应用。郑勇[18]基于简化线性特征线格式线性源方法开发了自适应性线性源方法，将线性源应用到矩阵特征线方法中。朱成林和郑勇是基于上述几种线性源方法挑选出其中一种将其应用到自己使用的程序中以达到完善程序完整性的目的，并不是方法研究。

本文提出一种采用最小二乘的线性源特征线方法，通过压水堆栅元及C5G7基准题的计算，与坐标投影线性源特征线方法和CASMO5中运用的线性源特征线方法进行对比分析。

1 理论推导

1.1 线性源特征线方法

在笛卡尔坐标系中，线性源特征线输运方程如式(1)所示：

(1)

(2)

式中：τ为光学长度，τ=Σtsm,i,k/sinθn；Γ1(τ)=1-e-τ；Γ3(τ)=2(τ-(1-e-τ))-τ(1-e-τ)。

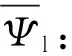
(3)

式中：ωn和ωm分别为中子方向Ωmn的极角权重和方位角权重；δAm为特征线密度；Vi为平源区i的体积。

1.2 最小二乘线性源特征线方法

本文提出了一种基于最小二乘的线性源特征线方法。首先假设源项分布为：

Q(x,y)=Qi+Qi,xx+Qi,yy

(4)

(5)

(6)

式中：Qi，x与Qi，y分别为平源区i内x、y方向的源项分布系数；(xc，yc)为特征线段的中点坐标；φm为方位角角度。

在各向同性条件下，根据中子源强的表达式可得到Qi，x与Qi，y：

(7)

(8)

假设中子角通量密度Ψ(x，y)为：

Ψ(x,y)=Ψ0+Ψxx+Ψyy

(9)

式中：Ψ0为某一网格内平均中子角通量密度；Ψx和Ψy分别为x和y方向的角通量密度分布系数。

将每条特征线的起点、终点及其平均通量代入式(9)，每条特征线段可得到3个方程：

(10)

根据上述公式可得到3倍特征线段数量的方程组：

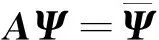
(11)

式中：(xin，yin)为某条特征线段的起点；(xout，yout)为某条特征线段的终点；Ψin、Ψc和Ψout分别为某条特征线段入射、平均和出射中子角通量密度；n为特征线段数量。

使用最小二乘法求解式(11)，即式(11)两端分别乘以AT得到正定方程组：

(12)

(13)

(14)

给定源项初值计算得到平源区内的标通量及标通量分布系数，再根据平源区内的标通量及标通量分布系数得到平源区内每条特征线段上的源强和斜率。

2 数值验证

通过压水堆栅元、组件问题及C5G7-MOX基准题验证最小二乘线性源特征线方法的计算精度，作为对比，同时给出平源近似特征线方法、坐标投影线性源特征线方法、CASMO5中线性源特征线方法的计算精度。本文给出的计算时间是在CPU为Intel(R) Core(TM) i7-8550U CPU@1.80 GHz、8G内存微机上运行结果，中子通量和keff的收敛判据分别为1.0×10-6、1.0×10-7。

2.1 燃料栅元算例

以单栅元69群算例进行验证，栅元几何模型包括4个区域，由内至外分别为燃料区、气隙、包壳及慢化剂区，几何尺寸如图1所示。多群截面通过蒙特卡罗程序统计得到。栅元的边界条件均为反射边界。栅元网格划分采用如图2所示的细网格和粗网格两种。

图3示出有效增殖因数的偏差Δkeff随网格数量的变化，计算条件为：特征线密度为0.01 cm，0°～360°内方位角数量为80个，Y-T求积组[19]极角数量为3个。选取48个网格下特征线线宽为0.001 cm、方位角数量为128的平源近似结果为基准解。由图3可看出，计算时网格数量越多计算得到的结果越精确，且随网格数量的逐渐增多，坐标投影线性源特征线方法和最小二乘线性源特征线方法的网格敏感性低于平源近似模型的特征线方法。最小二乘线性源特征线方法的Δkeff稳定在10～15 pcm范围内，比平源近似特征线方法更加准确。

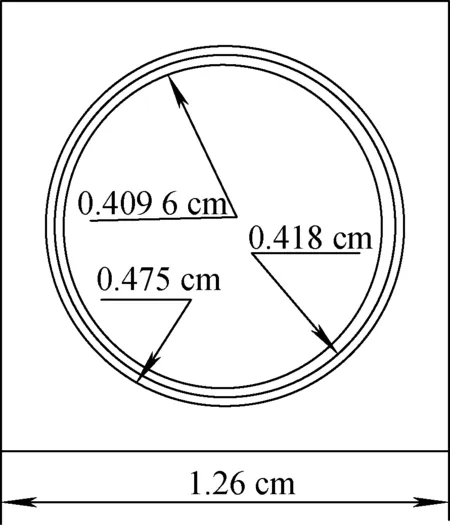
图1 燃料栅元几何尺寸示意图Fig.1 Schematic of fuel cell geometry

表1列出燃料栅元算例的计算结果。由表1可见，粗网格(8个网格)条件下，线性源特征线方法与平源近似特征线方法相比计算精度更高。线性源方法中，最小二乘线性源特征线方法的计算精度高于坐标投影线性源特征线方法。计算时间方面，在精度相当的细网格下，最小二乘线性源特征线方法的计算时间比平源近似特征线方法的更少。线性源特征线方法中，CASMO5在计算气隙时无法收敛。

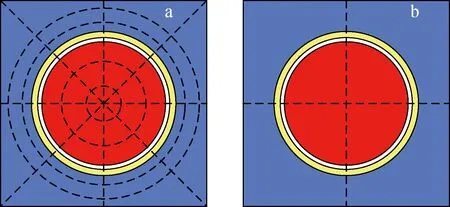
a——细网格；b——粗网格图2 燃料栅元网格划分示意图Fig.2 Schematic of fuel cell grid division

图3 燃料栅元算例Δkeff随网格数量的变化Fig.3 Δkeff change with mesh number in fuel cell problem

表1 燃料栅元算例的keff和计算时间Table 1 keff and calculation time of fuel cell problem

2.2 17×17燃料组件算例

以C5G7基准题[20]中燃料组件为计算对象，燃料组件是由导向管、UO2燃料栅元和裂变室组成，方形排列17×17元件的组件。组件的几何尺寸为21.42 cm×21.42 cm，组件中栅元布置方式如图4所示。栅元的具体几何信息如图5所示。网格划分采用如图6所示的细网格和粗网格两种。图7示出随网格数量逐渐增加不同方法进行输运计算得到的Δkeff，计算条件为：特征线密度为0.02 cm，0°～360°内方位角数量为96个，Y-T求积组[19]极角数量为3个。由图7可见，在8个网格时线性源特征线方法计算得到的精度达到了平源近似特征线方法使用40个网格数量计算精度。由于算例中不存在气隙，CASMO5中的线性源特征线方法计算过程中可收敛。随着网格数量的增加，4种方法计算得到的结果更加精确，且线性源特征线方法的网格敏感性低于平源近似特征线方法。

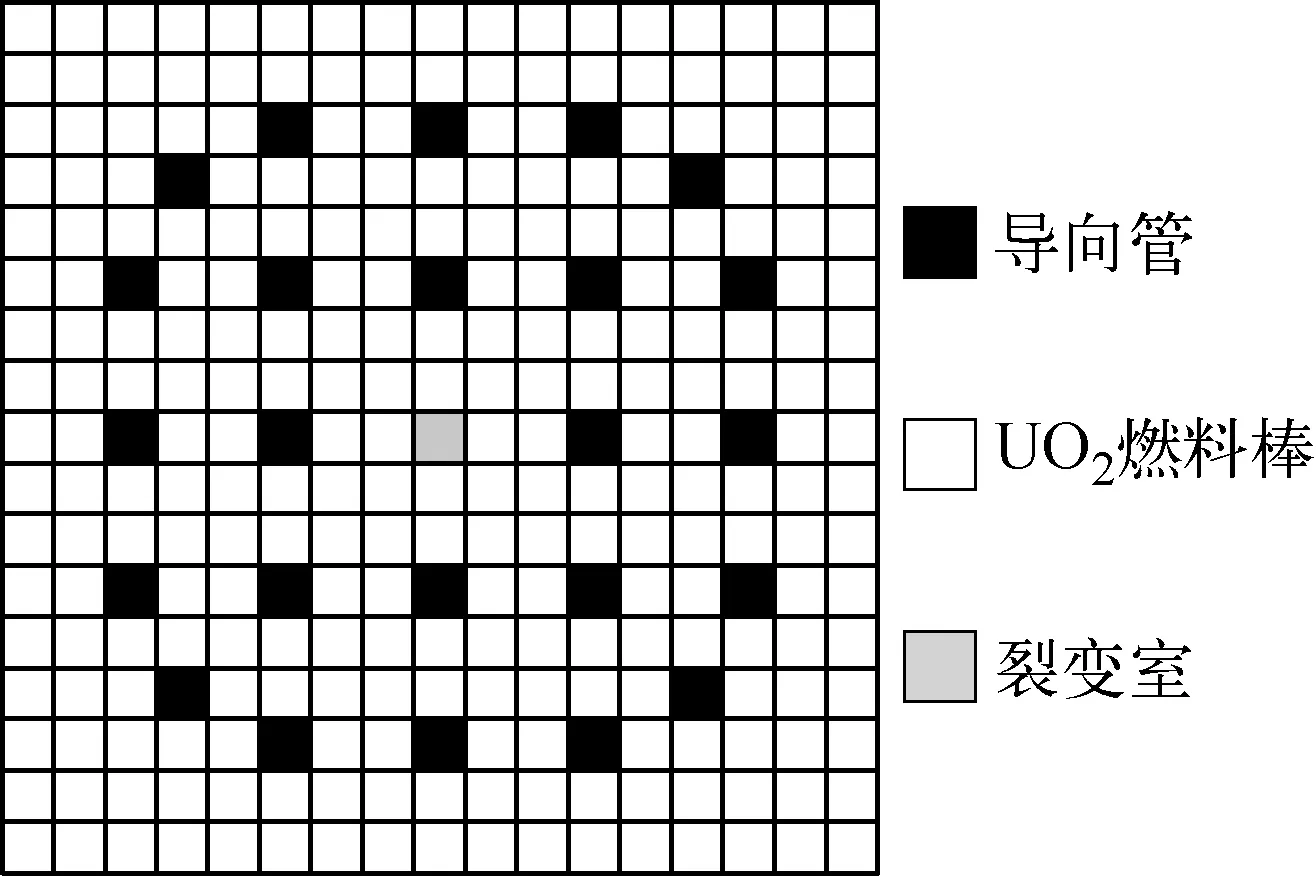
图4 栅元布置方式示意图Fig.4 Schematic of cell layout

图5 栅元几何尺寸示意图Fig.5 Schematic of cell geometry

表2列出燃料组件算例计算结果。由表2可见，在网格数量较少时，线性源特征线方法与平源近似特征线方法相比计算精度更高，且线性源特征线方法的计算精度与细网格下平源近似的计算精度相当。线性源特征线方法中，最小二乘与CASMO5的计算精度相当，且高于坐标投影线性源特征线方法。计算时间方面，最小二乘线性源特征线方法与细网格下的平源近似特征线方法相比，计算时间要更少。该算例验证了组件规模问题下最小二乘线性源特征线方法准确性较好。

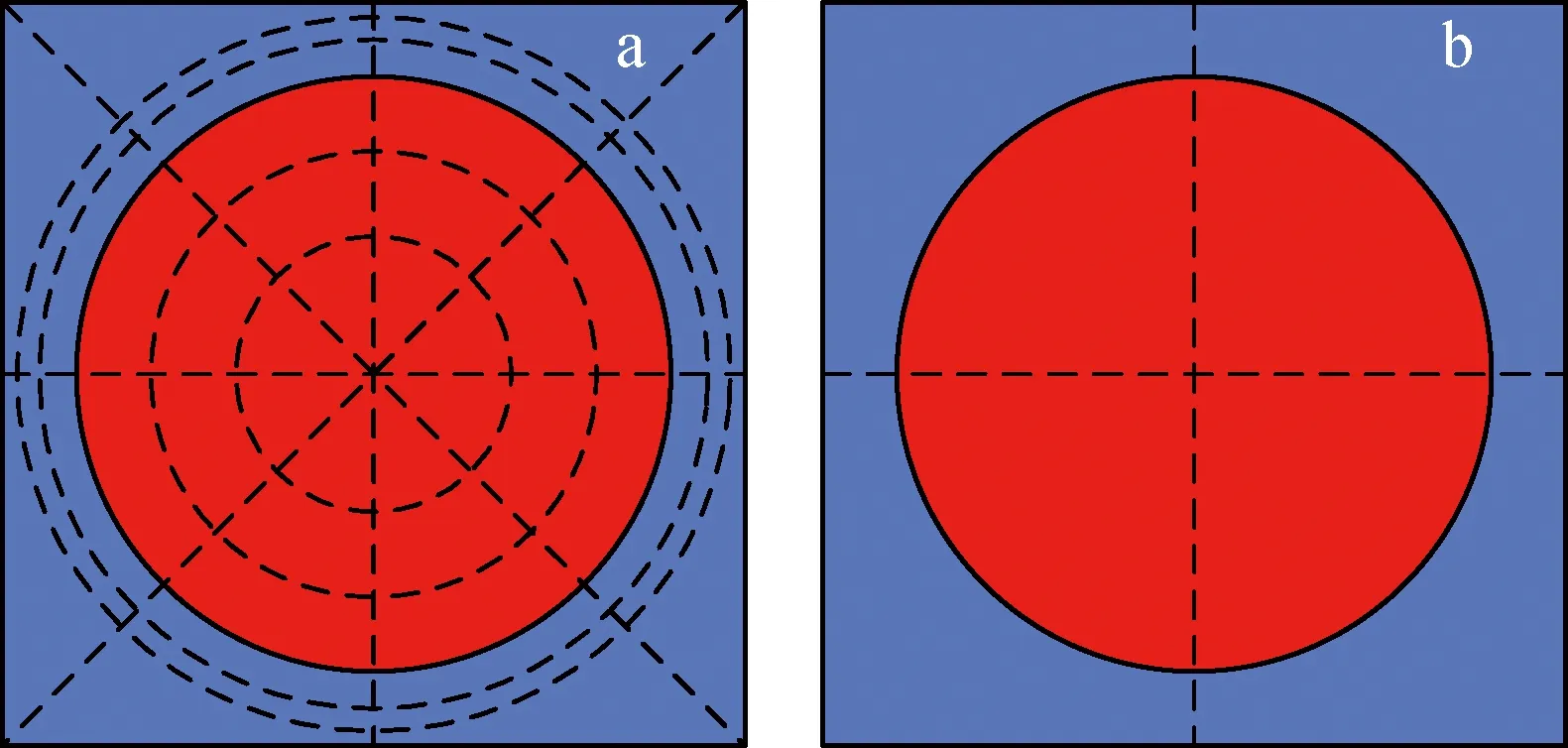
a——细网格；b——粗网格图6 栅元网格划分示意图Fig.6 Schematic of cell grid division

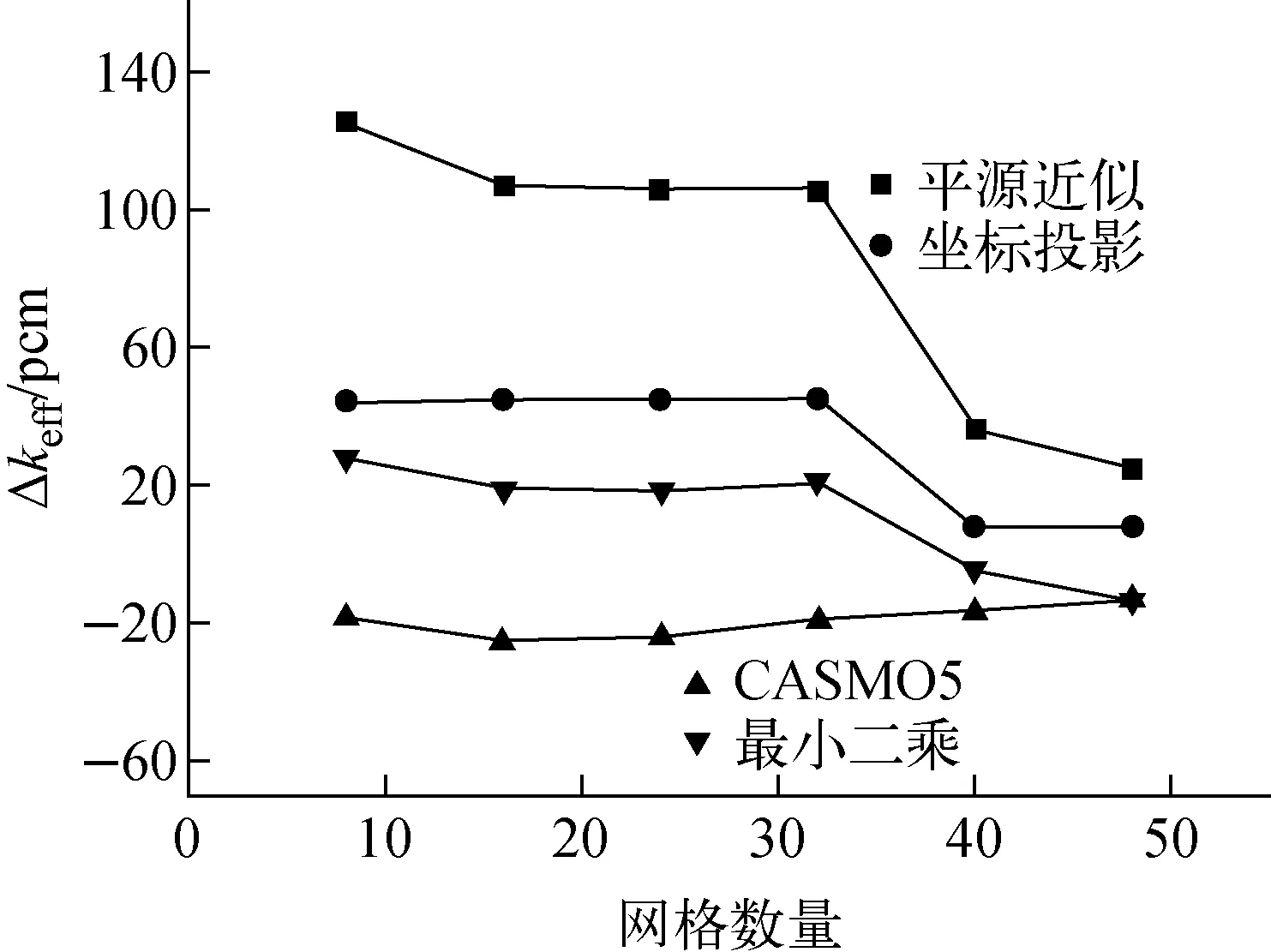
图7 燃料组件算例Δkeff随网格数量的变化Fig.7 Δkeff change with mesh number in fuel assembly problem

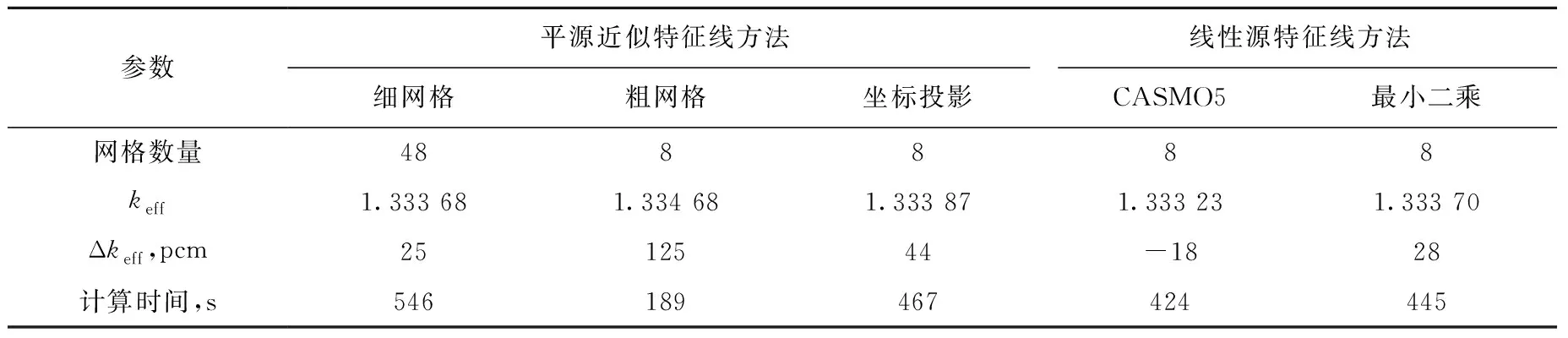
表2 燃料组件算例的keff和计算时间Table 2 keff and calculation time of fuel assembly problem

2.3 C5G7-MOX基准题

C5G7-MOX基准题[20]是由二氧化铀燃料组件和MOX燃料组件混合装载，共计16盒燃料组件，呈1/8对称。1/4堆芯布置如图8所示。每个组件的几何尺寸为21.42 cm×21.42 cm，反射层宽度为21.42 cm。二氧化铀组件和MOX组件均为17×17的排列方式。二氧化铀组件内燃料棒富集度相同，MOX组件内有3种含量不同的MOX燃料栅元，如图9所示。栅元几何尺寸与图5一致，网格划分方式与图6一致。C5G7-MOX基准题keff和计算时间的计算结果列于表3，功率计算结果列于表4。

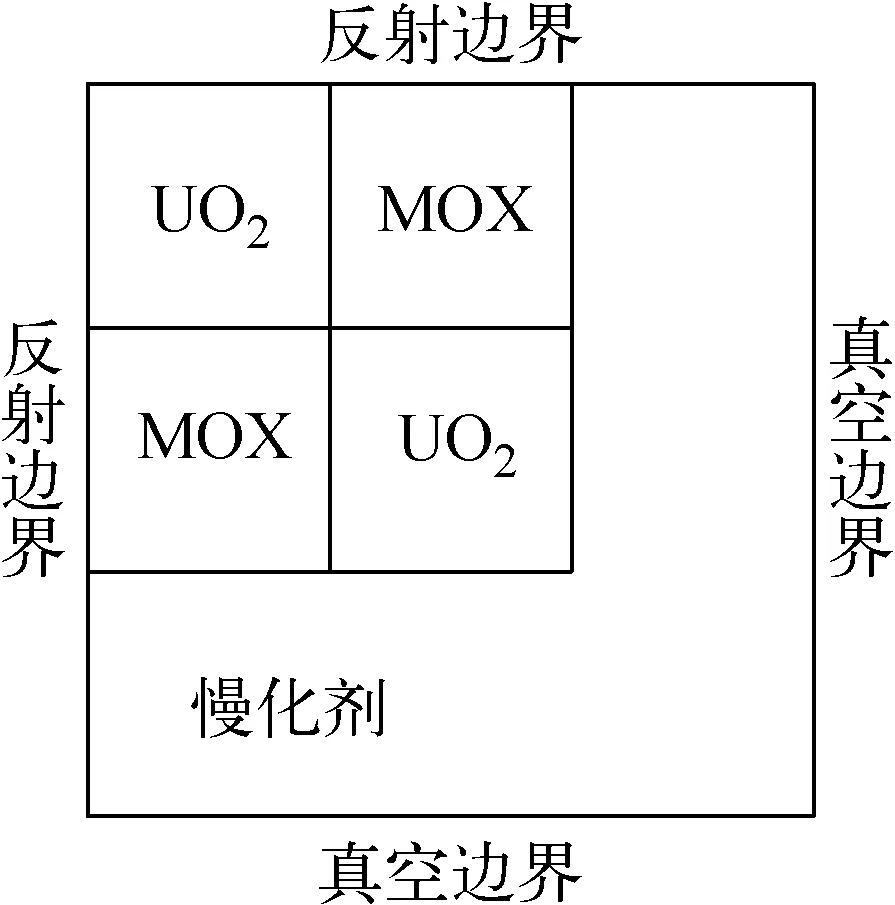
图8 1/4堆芯布置示意图Fig.8 Schematic of 1/4 core layout

图9 C5G7-MOX基准题组件几何布置示意图Fig.9 Schematic of component geometry layout for C5G7-MOX benchmark

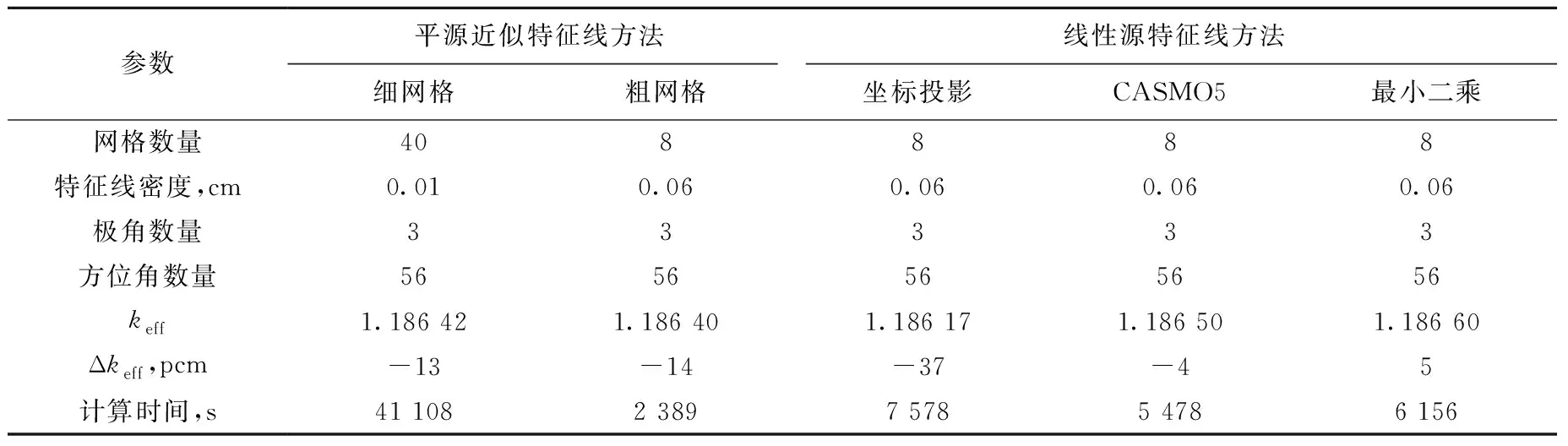
表3 C5G7-MOX基准题的keff和计算时间Table 3 keff and calculation time for C5G7-MOX benchmark

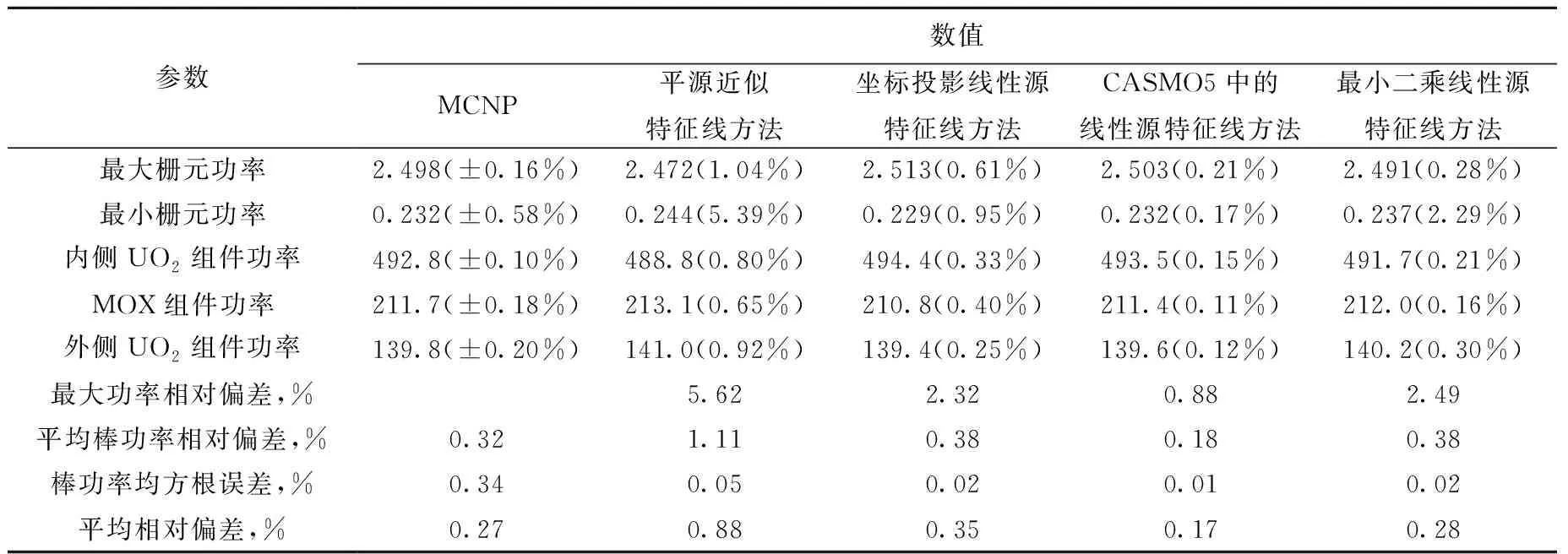
表4 C5G7-MOX基准题功率计算结果Table 4 Power calculation result of C5G7-MOX benchmark

由表3、4可见，用平源近似特征线方法进行计算，粗网格条件下的计算精度无法达到细网格条件下的结果。使用粗网格进行计算，线性源特征线方法比平源近似特征线方法计算精度更高，且线性源特征线方法的计算精度与40个网格下平源近似特征线方法的计算精度相当。线性源特征线方法中，最小二乘线性源特征线方法较坐标投影线性源特征线方法计算精度更高，且与CASMO5中的线性源特征线方法的精度相同。计算时间方面，两种线性源特征线方法比40个网格下的平源近似特征线方法的更少。功率水平方面，粗网格下线性源特征线方法的计算结果高于平源近似特征线方法的计算结果，CASMO5的功率计算结果更准确，最小二乘线性源特征线方法与坐标投影线性源特征线方法的功率结果精度一致。

上述数值结果验证了最小二乘线性源特征线方法的网格敏感性低且准确性较好。

3 小结

本文提出一种最小二乘线性源特征线方法，通过计算压水堆栅元及C5G7基准题等算例，得到以下结论。

1) 最小二乘线性源特征线方法能在网格数量较少的计算条件下得到较精确的计算结果，且计算精度可达到细网格下平源近似特征线方法的计算精度。

2) 在网格数量较少且输入条件相同时，线性源特征线方法比平源近似特征线方法更为准确。线性源特征线方法中，最小二乘线性源特征线方法比坐标投影线性源特征线方法更为准确，且与CASMO5中的线性源特征线方法的计算精度相当。

3) 最小二乘线性源特征线方法与相同精度下的平源近似特征线方法相比，计算时间更少。最小二乘线性源特征线方法与坐标投影线性源特征线方法相比，计算精度更高且网格敏感性更低；与CASMO5中的线性源特征线方法相比，最小二乘线性源特征线方法可直接处理带气隙的小网格问题，无需引入其他近似处理，适应性更好。