基于遗传算法的外汇量化交易策略优化研究

张华

北京经济管理职业学院，北京100102

一、引言及文献综述

近年来，随着金融学理论、数理统计理论的发展和完善，特别是随着计算机技术、优化算法的发展和创新，依靠信息技术、金融工程建模等手段来实现投资决策的量化交易方式正在影响金融市场，成为全球金融领域关注的一大焦点。目前，量化交易主要应用于基于数量化模型的技术指标交易、算法交易以及金融产品的错误定价等方面。其中，基于数量化模型的技术指标交易近年来发展最为迅速，它主要依赖一个混合的数量模型技术指标产生的交易信号来进行买卖。

遗传算法的出现为构建金融市场量化交易策略提供了新思路。遗传算法通过种群进化的方式寻找最优解，依靠并行搜索、全局寻优的优势可以快速计算出大量的优化数据，是一种兼顾计算效率和计算精度的策略优化方法。国内外学者从理论到实践进行了多种角度的深入探讨。Chen等（2008）将遗传算法和多种技术指标组合应用于股票市场，成功找到了可获利的交易规则。Jiah-Shing Chen 等（2009）指出遗传算法可用来解决投资组合策略问题，通过遗传算法可提高技术交易指标策略的绩效。赵建等（2011）将遗传算法运用在国内期货市场上，证明遗传算法可以优化单个和多个量化交易策略的参数。刘伟等 （2015）采用MACD指标和KDJ指标构建量化交易模型，运用沪深300指数的历史交易数据进行回测检验，证实技术指标组合对提升量化交易策略的盈利水平有一定帮助。Yuri Zelenkov（2017）使用遗传算法对历史交易数据进行优化，使得量化交易策略买入和卖出信号的准确率显著提升。林杰等（2018）分别构建了基于顺势指标（CCI）和相对强弱指标（RSI）的单指标量化交易模型，并使用大连商品交易所的棕榈油期货品种验证了模型的有效性。麦根（2019）构建了基于MACD指标和RSI指标的双指标量化交易策略，并使用遗传算法对交易策略进行参数优化，选取欧元兑美元的历史交易数据对该交易策略的交易绩效进行检验，结果表明技术指标组合量化交易策略在盈利和风险方面比单指标量化交易策略有更好的表现。

从上述国内外研究现状来看，运用人工智能算法实现基于技术指标的量化交易择时策略己非难事。但大多数情况下，基于默认技术指标参数构建的量化交易择时策略的表现却比较一般，也较难适应不同市场和不同时间的行情走势。通过对技术指标量化交易策略进行参数优化，可适应具体交易标的的行情走势、提高量化交易策略的盈利能力、降低风险，使量化交易策略的效用达到最大化。因此，量化交易的难点己从构建策略转移到优化策略。

针对上述问题，本文构建了基于遗传算法的外汇量化交易策略优化模型。首先，该模型在训练区间内将技术指标及指标参数随机构成的量化交易策略进行优化，并应用于后继的测试区间，可不再依赖对流行的技术交易策略的先验知识。在测试区间上通过采用移动视窗技术对该模型的性能进行评估，真正实现了样本外测试，避免了“数据探测偏差”（Data Snooping Bias） 的发生。其次，该模型系统根据输入的汇率收盘价训练数据，通过遗传算法自适应地产生最优量化技术交易策略，该策略可根据训练区间的市场环境改变而进行相应地调整和优化。

二、遗传算法过程

遗传算法（GA）通过模拟生物进化的过程来搜寻最优解。算法中的个体应用在技术分析中对应某一交易策略，个体使用二进制字符串来表达，字符串中的每一个字符对应一个基因。首先，随机生成由一定数量个体组成的初始种群，根据优化目标使用确定的适应度函数，在训练区间上对每个技术交易策略进行评估。其次，种群再通过复制、交叉和变异等进行逐代进化，当达到预设的进化终止条件时进化停止。此时，当代种群中具有最高适应度数值的技术交易策略即为最优量化交易策略。此后，最优策略进入测试区间进行样本外性能评估。

三、基于遗传算法的外汇量化交易策略优化模型

基于遗传算法的外汇量化交易策略优化模型框架结构如图1所示。该模型以汇率历史收盘价作为输入数据、以遗传优化算法为核心模块、以技术分析为理论基础，通过算法优化生成具有自适应性的最优量化交易策略，使用测试数据集检验策略的盈利能力。首先，模型将训练数据集的汇率历史收盘价转换成多种技术指标，之后将技术指标生成的买入和卖出信号作为输入数据，通过种群初始化，再通过复制、交叉、变异等子模块进行进化，并以最大收益率作为适应度函数，最终将得到的最优量化交易策略应用于测试区间，验证交易策略的效率。

图1 基于遗传算法的外汇量化交易策略优化模型框架图

（一）输入训练数据集

本文使用的数据集是外汇交易市场中主要货币欧元兑美元（EUR/USD）、英镑兑美元（GBP/USD）的汇率历史收盘价数据，频率是60分钟，交易模型每隔1小时分析一次交易信号。

（二）选取技术指标

根据技术指标使用的原则及所研究问题初始种群编码的切实可行性，结合外汇市场连续性、高流动性、波动性强的三大特征，本文选取一种趋势性技术分析指标即指数加权移动平均指标（Exponentially Weighted Moving Average，EWMA）和三种震荡型技术分析指标,即相对强弱指标（Relative Strength Index，RSI）、乖离率指标（Bias Ratio，BIAS） 和变动率指标 （Rate of Change，ROC）组合形成量化交易策略。

（三）求解最优量化交易策略优化模型

1.创建初始种群

本文中初始种群规模（即种群中个体数目）设为200。由于种群中个体的编码方式是设计遗传算法成功与否的关键，因此根据规则中技术指标和指标参数取值范围，种群中的个体采用二进制多参数级联编码，个体由3部分组成（如图2所示）。其中，RSI1代表相对强弱指标；BIAS代表乖离率指标；ROC代表变动率指标，指当前汇率相对于1小时之前上升或下降的比率；RSI2表示对指数加权移动平均计算其相对强弱指标值。

表1显示的是交易策略应满足的条件方程，表中的参数c1～c8分别对应图2中各个指标的上下限取值，Op.1、Op.2、Op.3 分别表示逻辑运算符“and”或者“or”。

图2 个体编码示意图

表1 条件方程

图2中，第一个55位二进制表示买策略，将这55个二进制位平均分成11组，每组包含5个二进制位。这5个二进制位可表示32个数值 （1位二进制能表示2种状态“1或者0”那5位二进制组合起来就是2*2*2*2*2=32种状态）中的一个，这32个数值就是该组取值的最大值和最小值之间的可能值。前8组（40位）代表上述4个指标的上下限，每5个二进制位代表一个限值。如果4个指标的当前值就在此范围内，则显示买信号。后3组（15位）代表指标中的参数取值。第二个55位表示卖策略，卖策略的编码方式与买策略相同。后8位表示决定交易时机的交易策略，其中，前面3位是逻辑运算符“and”或者“or”，后面 5 位用来决定训练策略。如果这个策略的评估值是“TURE”，则交易执行；否则，表示该段时间内不执行交易。

2.计算适应度

在遗传算法中用适应度函数来评估个体的优劣，以作为优胜劣汰的依据。本模型中，针对每一时间段的训练数据，寻找该时段对应的最优量化交易策略是优化的最终目标，然而衡量一个交易策略是否最优主要看该策略对应的投资收益是否最大。因此，将交易策略对应的投资收益作为适应度函数。

3.选择运算

本文采用联赛选择（Tournament Selection）算子，每次选取几个个体之中适应度最高的一个个体遗传到下一代群体中。联赛选择中，每次进行适应度大小比较的个体数目称为联赛规模，本文联赛规模取值为50。除此之外，为了保留高适应度的个体，将适应度值排名前1%的个体自动保留下来。另外，适应度值排名在后30%的个体被随机产生的新个体取代，具体如图3所示。

图3 新种群生成过程示意图

4.交叉和变异

本文采用两点交叉算子，交叉概率为60%；变异运算的概率设为1%。重组后采用两点交叉，经过变异运算后获得新的种群。

5.终止条件

算法的终止条件可以取某个固定的进化代数，一般为50-100，或者最好个体的适应度值连续10次不再提高，这个最好的个体即为优化后的量化交易策略。

本文使用代沟为0.9，最大遗传代数为100。重复上述过程，直到遗传代数达到算法设定的数值。

投资过程的详细流程如图4所示。每隔1小时，模型就会自动检查表1中条件方程各个技术指标的当前值。如果在时刻t所计算的指标值满足买策略或者卖策略，则交易模型系统就会买进外汇或者卖出外汇。如果在同一时点，有两个方程同时满足条件，则该个体无效，此时该个体的适应度值自动置为0。

图4 投资过程流程图

四、实证检验

（一）数据资料

本文选取Meta Trader 5.0外汇交易平台中EUR/USD和GBP/USD在2018年1月2日至2019年12月31日之间频率为1小时的汇率收盘价数据（共计24623个）进行实证检验。将研究数据分为训练区间和测试区间，前者用于优化交易策略，后者用于评估测试交易策略的盈利能力。为避免“数据探测偏差”的发生，本文采用移动视窗技术以固定的步进值将数据划分为多组互相重叠的训练区间和测试区间。将前六个月的数据作为训练区间，之后三个月的数据作为测试区间进行一次评估，然后将整个测试步进三个月。因此，两年的数据可以产生六个重叠但相对独立的测试区间，如图5所示。

图5 训练和测试方法示意图

（二）初始资本及交易费用

分别针对上述两种货币进行独立交易，初始资本均设为10000，交易费用设为2个点差（2bp），使用 1∶1 的杠杆比例（即无杠杆），以避免杠杆比例带来的额外风险。

（三）实证分析

1.最优量化交易策略分析

以2018年1月2日至2018年6月30日，频率间隔为1小时的GBP/USD汇率数据作为训练数据集，利用上述方法选择该区间内的最优量化交易策略，如表2、3所示。从表2中可以看出，该区间选出的最优交易买策略满足表1中的条件方程B，最优卖策略满足表1中的条件方程A。进一步分析，该时段的最优买策略中指标RSI2的取值范围是[16.32，25.13]，而不是经验上认为的[0，30]，这样可以减少交易的次数，提高交易信号的准确率。再者，针对GBP/USD货币，1小时的频率间隔，其指标RSI的最优参数是21，而不是习惯上认为的9或者14。利用训练数据集（2018年1月—6月）搜索到的最优交易策略，在该训练数据集的收益为16.15%，而买卖持有策略的收益仅为-2.26%。将搜索到的最优量化交易策略进行为期3个月 （2018年7月—9月）的测试。实证结果显示，这段时期其所获得的收益为7.96%，而买卖持有策略的收益为-1.26%。因此，在实际投资操作中，对于外汇交易或者股票交易，一味地使用经验数据是有很大弊端的。

表2 最优量化交易策略示例（买策略，GBP/USD，训练时段：2018年1月—2018年6月）

表3 最优量化交易策略示例（卖策略，GBP/USD，训练时段：2018年1月—2018年6月）

2.算法性能分析

图6和图7分别为GBP/USD、EUR/USD的汇率数据对应的遗传算法进化过程示例图。图中横轴表示进化代数，纵轴表示适应度（收益率）。图中的实线表示各代的最大收益率，虚线表示各代的平均收益率。

从两个图中均可以看出，在交易策略的进化过程中，群体中个体适应度的最大值和平均值虽然均呈现波动状态，但总体上还是呈现出一种上升的趋势，说明该模型算法比较稳健地实现了最优量化交易策略的收敛。当模型算法迭代到80-100代的时候，两种汇率基本上都搜索到了最优的交易策略。从算法的计算性能来看，足以证明该遗传算法具有良好的优化性能。

3.年收益率对比分析

图6 100次迭代后各代最优量化交易策略对应的最大收益和平均收益的变化曲线图（GBP/USD）

图7 100次迭代后各代最优量化交易策略对应的最大收益和平均收益的变化曲线图（EUR/USD）

为了更好地衡量基于遗传算法的交易策略优化模型的表现，本文将基于GA策略模型的实证结果和“买入-持有”策略及基于Dempster-Shafer证据理论的外汇交易策略进行比较。针对GBP/USD、EUR/USD（2018—2019年）每一种汇率数据分别做实证检验，将每6个月寻找到的最优交易策略应用到随后3个月的测试数据集，分别计算其年收益率，结果如表4所示。从表中第一行可以看到，基于GA方法的年收益率都在20%以上，远远高于“买入-持有”策略的收益，获得了较高的超额收益。

基于GA方法的年收益率比基于Dempster-Shafer证据理论方法所产生的年收益率还高11-14个百分点。分析其原因大致有两点：第一，基于D-S证据理论的交易策略中，对指标参数的选择以及技术指标的使用主要基于经验和主观选择，投资中的非理性因素起了很大作用。而基于GA的方法，其指标的组合及指标中的参数是随着交易币种和交易时间进行调整和优化的；第二，基于D-S证据理论的交易策略中，在构造证据个体对应的基本概率分配函数时，也需要估算概率分配函数中的参数，该参数的选取是通过大量实验选择的，有一定的误差。因此，基于GA的方法较其它两种算法都具有更大的优势。

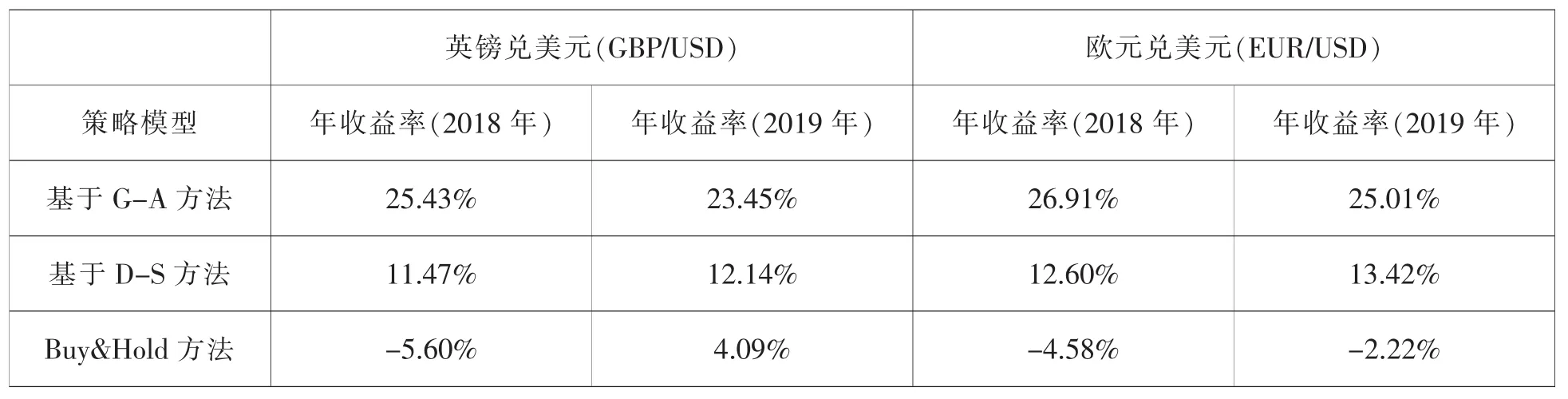
表4 年收益率对比分析表

五、结论

本文选取技术分析指标构建了基于遗传算法的外汇量化交易策略优化模型，该模型运用遗传算法对量化交易策略的参数进行优化，找出符合市场交易行情的最优交易策略所对应的指标组合和指标的最佳参数、通过全局随机搜索能力判断买入卖出点、采用移动视窗技术避免了数据探测偏差的产生。使用英镑兑美元、欧元兑美元的历史价格数据进行实证检验，研究结果表明，基于遗传算法的外汇量化交易策略优化模型所获得的年收益率要远远高于“买入-持有”策略，比基于Dempster-Shafer证据理论方法所产生的年收益率也要高。这也间接反映了外汇市场是非有效的，存在一定的套利空间。