基于EMD 与BP 神经网络的齿轮故障诊断
2021-01-21刘剑生王细洋
刘剑生 , 王细洋
(南昌航空大学 通航学院,南昌 330063)
0 引言
齿轮是机械设备中最常见的机械传动零件,它拥有结构紧凑、效率高、寿命长等优点,因此广泛应用于机械传动中。同时,由于工作在高速、重载等恶劣环境下,齿轮发生故障的概率大大增加。齿轮一旦出现故障,还会诱发其他机械零件故障,造成巨大的损失,甚至导致人员伤亡;因此,对齿轮故障诊断的研究至关重要。
近年来,由于BP 神经网络具有较强的模式识别能力、高度的自学习和自适应的能力,一些专家学者已经将其应用到齿轮的故障诊断中,并且取得了一定的成果。王勇[1]、闫君杰[2]等通过计算故障信号的均值、峰值、峭度和裕度等特征指标,再将特征指标归一化后作为BP 神经网络的输入,达到了对齿轮故障分类的效果,但是采用单一的BP 神经网络对齿轮故障进行分类,误差较大,网络训练速度慢。龙泉等[3]采用粒子群优化BP 神经网络方法减少了该算法易陷入局部最优解的风险,加快了网络收敛速度,提高了效率。但是对于信号的预处理方面尚有欠缺。此外,陈学峰等[4]提出了双谱−BP 神经网络的故障诊断方法,并以双谱为BP 神经网络的输入特征向量对齿轮进行故障模式识别,该方法有一定的分类效果,但是其过程过于繁琐,网络的训练速度以及准确率并不理想。
针对上述问题,本研究采用EMD 与BP 神经网络相结合的方法对齿轮故障进行分类。使用EMD 方法对采集到的非平稳信号进行处理,提取出故障信号的若干IMF 分量,此时能够对信号进行比较直观地分析。对分解出的各个IMF 分量的能量进行计算,区分各类故障齿轮中各个分量的能量分布特点。这些由能量组成特征向量是神经网络训练的有效依据。将这些特征向量作为BP神经网络的输入也较为合理;因此,采用EMD 与BP 神经网络相结合的方法以减小训练误差和提高网络训练速度。
1 EMD 与BP 神经网络基本原理
1.1 EMD 基本原理
EMD 是20 世纪90 年代Huang 等[5]提出的一种对非平稳信号的处理方法,可将信号分解成平稳的若干本征模式分量(IMF 分量)以及剩余分量。在时域信号中,以不同时间尺度为基准,分解出若干个本征模式函数IMF,其分解出的IMF 分量包含原始数据不同时间段的局部特征。其分解步骤如下所示:
1)从初始信号x(t)中取出其所有局部极大值点,在这些局部极大值点都大于相应x(t)中的点前提下,将这些极大值点用3 次样条曲线依次连接,得到极大值样条曲线l(t)。然后以同样的方法得到x(t)的极小值样条曲线s(t)。取2 个样条曲线的均值序列m(t):
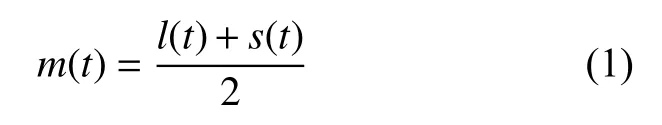
2)在原始信号x(t)中,减去上、下2 个样条曲线的均值序列m(t),得到:
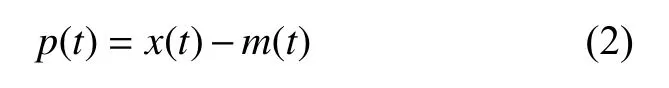
以基本模式分量的2 个条件为标准,判断所得到的p(t)是否同时满足该条件。如果不满足,则将p(t)当做初始信号x(t),重复步骤1、2 的操作,直至p(t)是一个基本模式分量,记为:

3)记剩余值序列为r1(t),则:
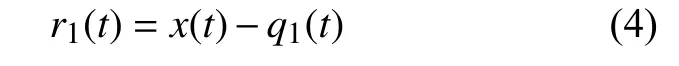
4)将r1(t)当做初始信号x(t),重复步骤1~3 的操作,可得到n 个基本模式分量c1(t),c2(t),…,cn(t),最后剩下原始信号的余项rn(t)。此筛选过程设定停止准则,最后初始信号x(t)被分解为若干基本模式分量ci(t)和一个剩余项rn(t),即:

1.2 BP 神经网络基本原理
BP 神经网络算法包括2 个步骤[6]:信号的前向传播和误差反向传播。按结构划分,又分为输入层、隐含层和输出层。其中输入层和隐含层、隐含层和输出层之间采用全连接方式连接。隐含层可以有一层或多层。
1)信号的前向传播。
隐含层第i 个节点输出oi为:
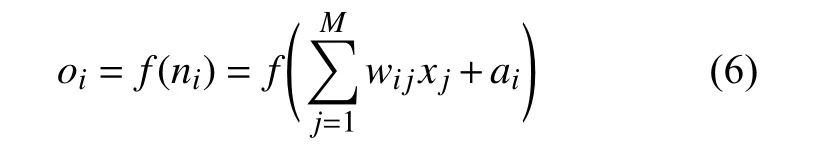
其中:wi,j为连接隐含层中第i 个节点与输入层中第j 个节点的权值;xj表示输入层第j 个节点的输入,j=1,…,M;ai为隐含层第i 个节点的阈值;ni为隐含层第i 个节点的输入;f 为隐含层激活函数。
输出层第k 个节点的输出ok为:
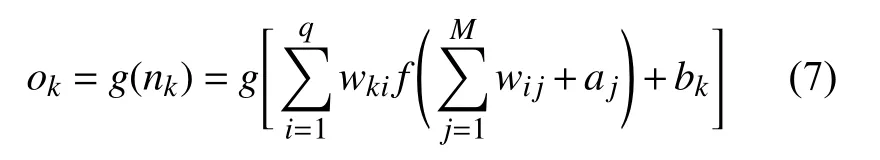
其中:wk,i为连接输出层中第k 个节点与隐含层中第i 个节点的权值,i=1,…,q;bk为输出层第k 个节点的阈值;nk为输出层第k 个节点的输入;g 为输出层激活函数。
2)先由输出层的结果开始计算其与实际值之间的误差,再以此为结果计算各层神经元的误差。然后通过这些误差,根据梯度下降法来更新连接输入层、隐含层、输出层之间权值和阈值。
设定计算误差的准则函数Ep为:
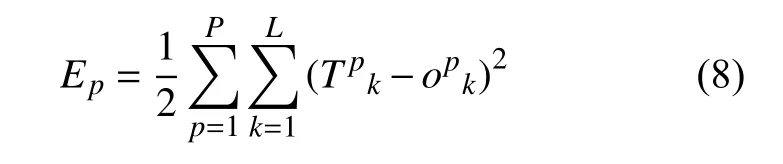
根据梯度下降法依次更新输入层、输出层、隐含层的权值修正量和阈值修正量:
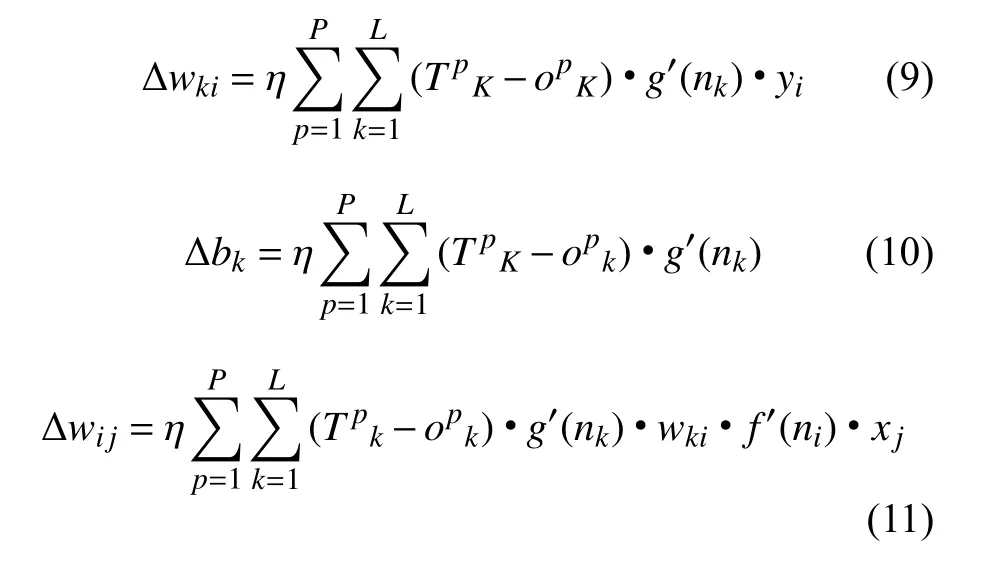
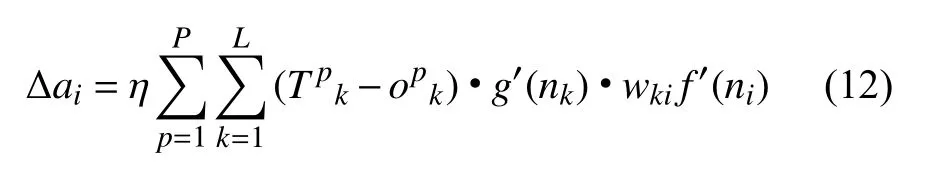
其中:Δwki为输出层权值修正量;Δbk为输出层阈值修正量;Δwij为隐含层权值修正量;Δai为隐含层阈值修正量;为预设输出值;η 为学习率;yi为输出层第i 个节点的值;为实际输出值。
2 基于EMD 和BP 神经网络的故障诊断方法
2.1 EMD 方法特征量提取
根据EMD 方法对故障信号分解出的IMF 分量进行分析,选取每个信号分解所得的前8 个分量。
分别求取前8 个分量的能量[7]:
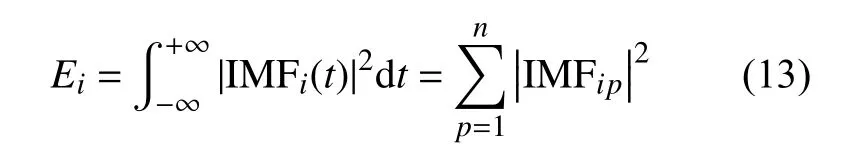
计算信号的总能量:
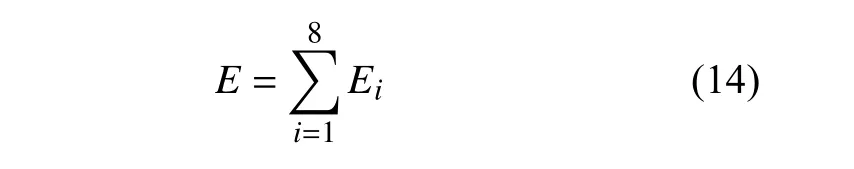
构造归一化后的能量特征向量:
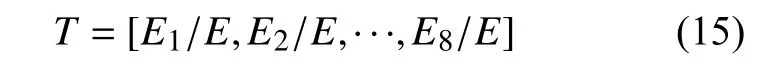
2.2 BP 神经网络建模
1)数据归一化。尽管得出的能量特征向量已经是归一化后的值,但为了使特征指标的数值都处于[0,1],还需对其进行归一化操作,归一化公式为:
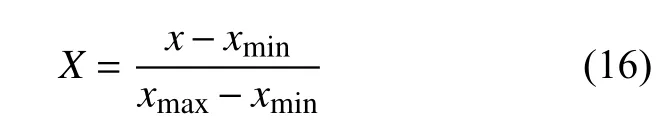
2)确定神经网络隐含层和输出层节点数。EMD 方法所提取出的特征向量为8 维,因此,构建的 BP 神经网络的输入层为X1~X8 的8 个特征指标,即输入层神经元数目为8;输出层节点数的选择是以模型识别模式的数量为依据,根据实验要求,本研究有4 种工作状态的齿轮,分别为正常、缺齿、齿根裂纹和齿面磨损,因此确定输出层神经元数目为 4。
定义神经网络的输出值为四维向量,对输出向量进行编码,如表1 所示。
计算神经网络隐含层节点数目[8-10]:
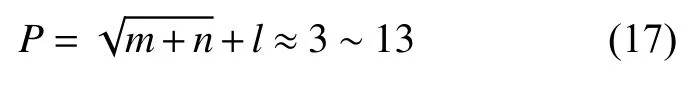
其中:m 为输入层节点数,m=8;N 为输出层节点数,n=4;l 为1~10 的整数。

表1 齿轮状态编码Table 1 Gearbox status code
因此,可得网络隐含层神经元的取值空间[5,6,…,13],在集合空间内尝试对神经网络训练,结合实践经验最终确定隐含层神经元数为10。
3)神经网络模型,如图1 所示。X1~X8 为输入特征向量,W1、W2 为权重参数,Y1~Y4 为决定4 种故障类型的向量。
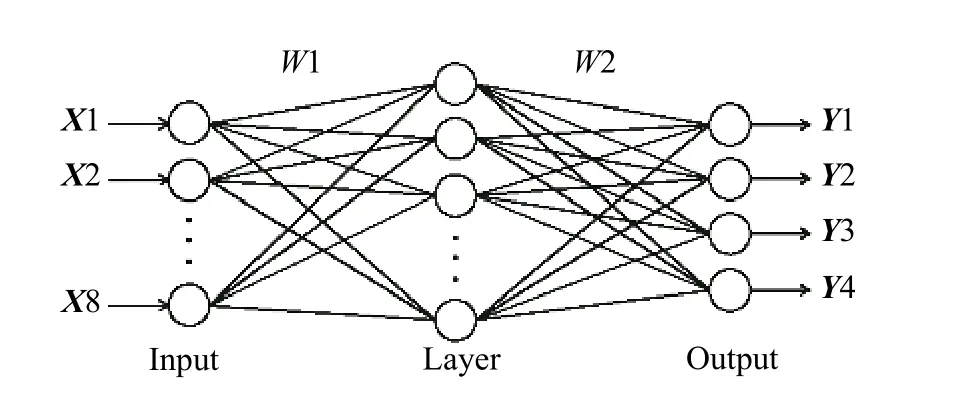
图1 神经网络模型Fig.1 Neural network model
3 实验验证
3.1 齿轮传动故障信号采集
实验台如图2 所示。采样频率为20.48 kHz,电机转速为1800 r/min。分别对正常、缺齿、齿根裂纹、齿面磨损的4 种类型齿轮(图3)磨损进行信号采集。每种故障采集16 组数据,每组数据采样点数为16 384,实验一共获取64 组采样数据。

图2 实验台Fig.2 Experiment rig
3.2 数据处理和网络训练
对已采集的数据进行整理分类,使用MATLAB软件进行EMD 方法编程,得出其各个IMF 分量图,如图4 所示。

图3 4 种类型齿轮Fig.3 Gears of four states
按照EMD 方法对振动信号进行分解之后,结合图4 对分解出的各个分量进行简单分析,发现被测4 种类型波形图有较大的区别。靠前的几个IMF 分量的振幅相对较大,也是振动信号所蕴含的能量主要集中的地方。图5 所示为4 种信号分解出的前8 个分量能量图,显然,每种故障信号的能量分布有较为明显的特点,以此作为BP 神经网络的输入将会有良好的效果。
将得出的所有能量特征向量进行归一化操作,归一化后的数据即可作为神经网络的输入样本数据,其部分样本数据和对应的齿轮箱状态如表2 所示。
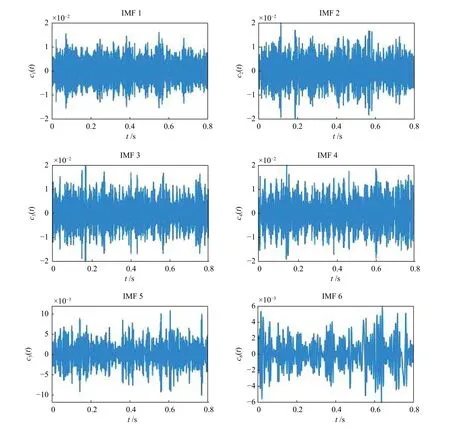
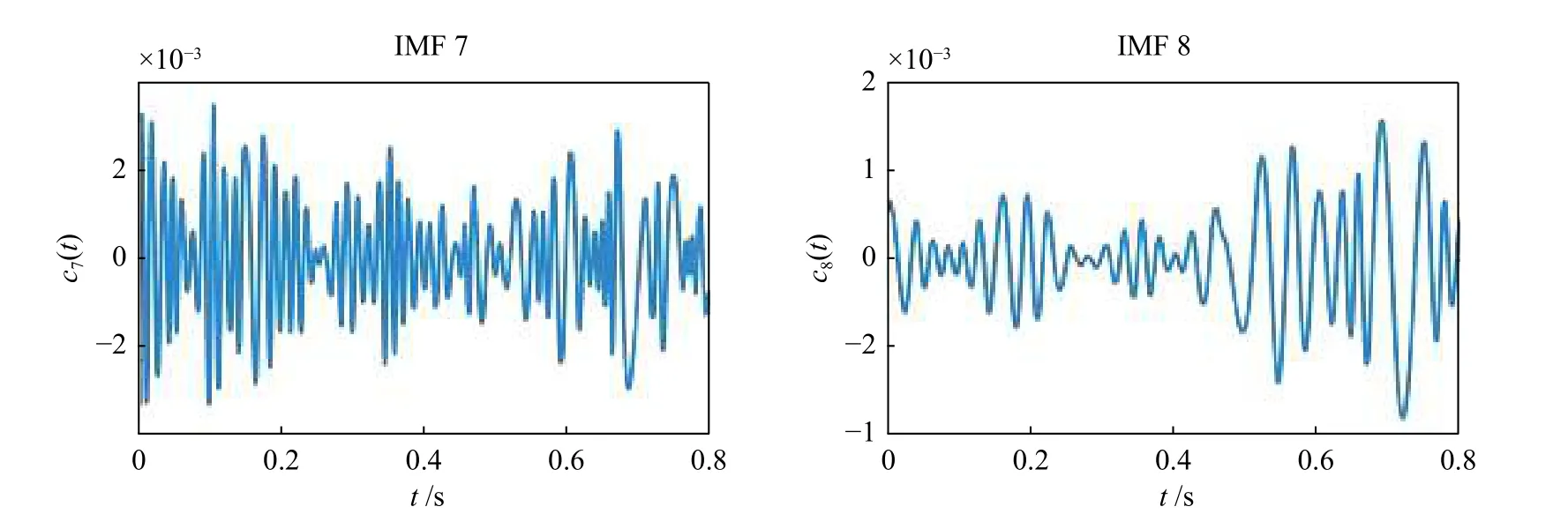
图4 齿根裂纹EMD 波形图Fig.4 EMD decomposition of root crack
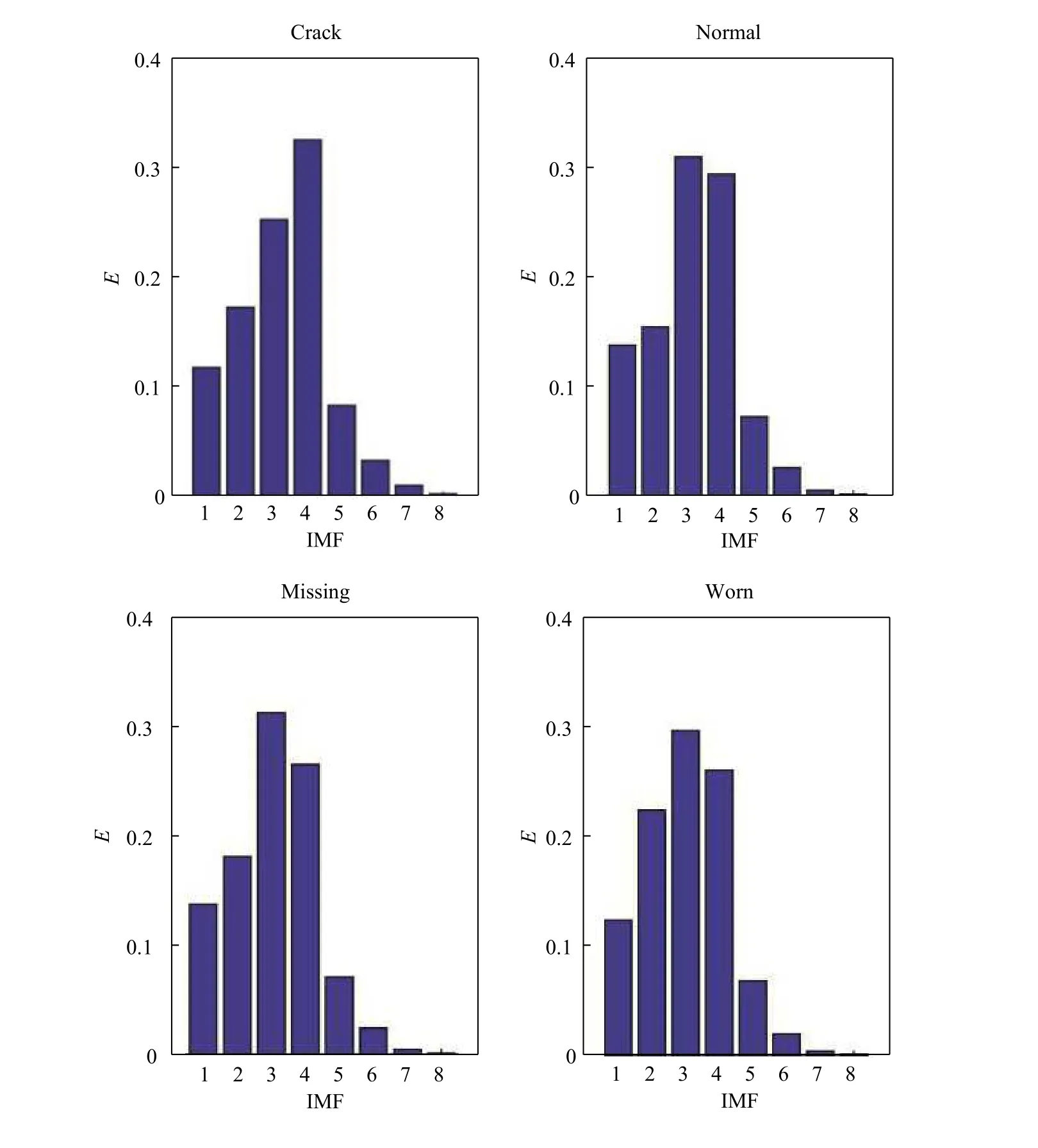
图5 IMF 能量图Fig.5 IMF energy
实验所得样本数据一共64 组,将这64 组样本数据作为BP 神经网络的输入,4 种模式的特征向量为输出。其中,使用MATLAB 编程,随机选取48 组数据作为训练集,另外16 组数据作为测试集。然后,设定神经网络参数。网络隐含层和输出层传递函数均选用Sigmoid 函数,训练函数采用trainlm 函数[11-12],设定学习率为0.01,最大训练次数1000,期望误差0.001。
3.3 诊断结果分析
图6 为对传统BP神经网络进行训练之后的误差图,图7 为采用本研究所提出的EMD 与BP 神经网络方法进行训练之后的误差图。通过误差图可了解到网络迭代次数与均方误差之间的关系。
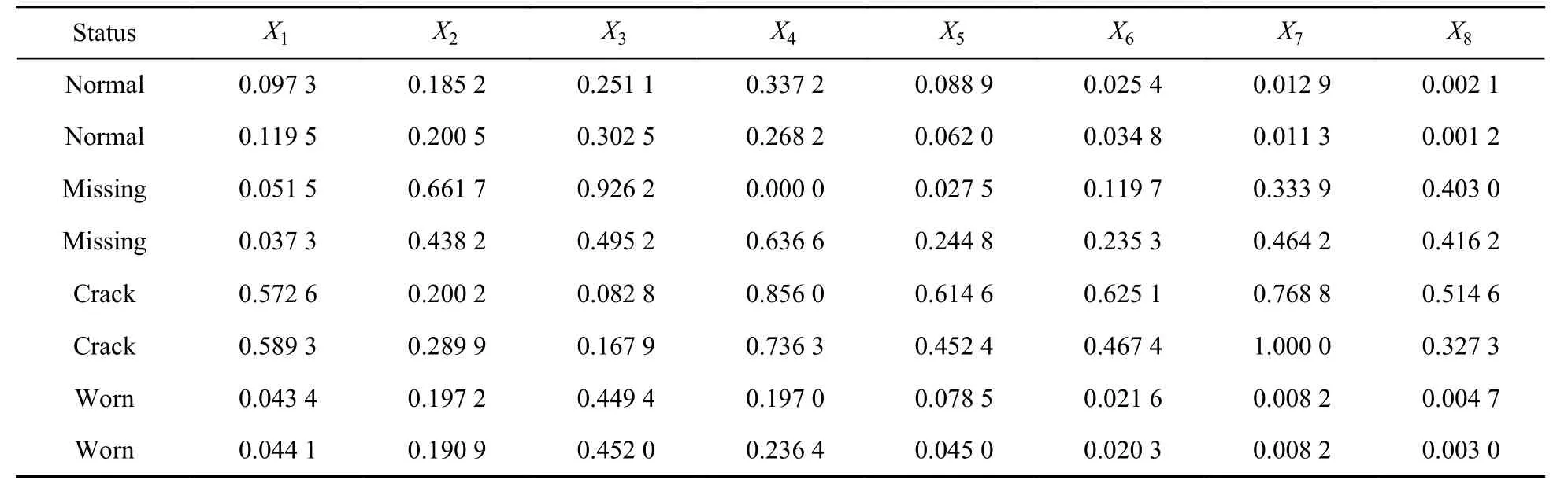
表2 输入样本数据Table 2 Input sample data
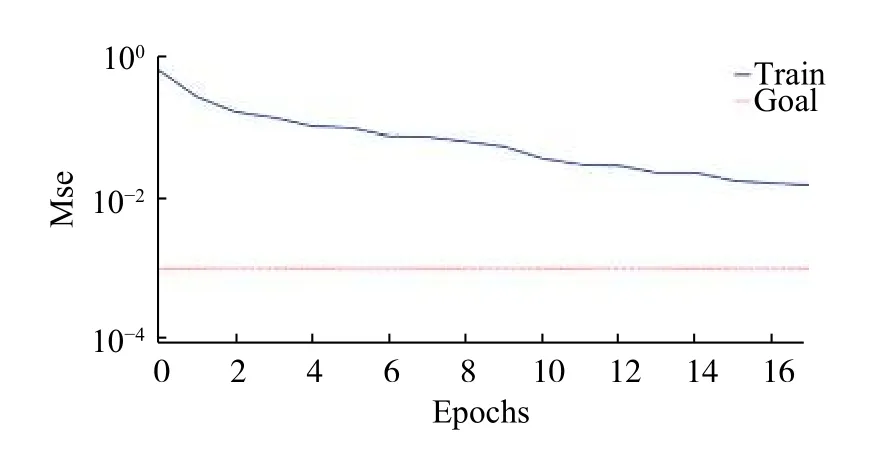
图6 BP 神经网络误差图Fig.6 BP training error
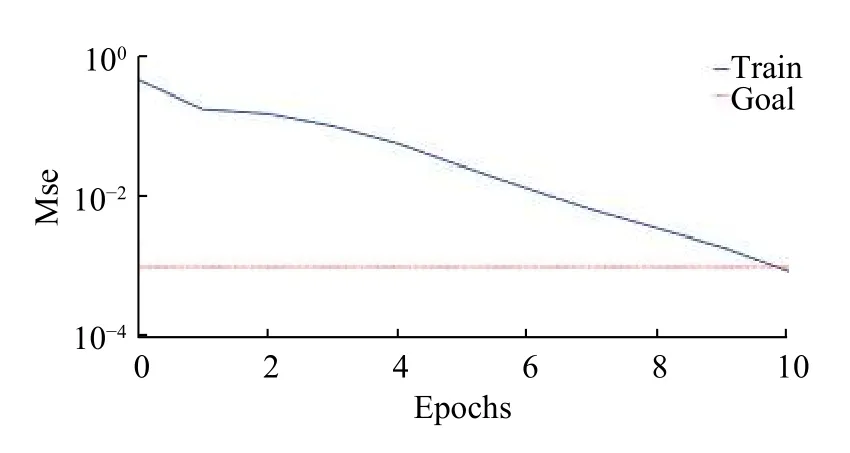
图7 EMD 与BP 神经网络误差图Fig.7 EMD and BP training error
对比图6、图7 可以看出,相对于单一的BP神经网络诊断方法,结合了EMD 算法的BP 神经网络的方法误差相对较小,达到了期望误差0.001。图7 仅经过了10 次迭代便达到了预期效果,相比之下,提高了网络训练速度。
为了进一步对训练好的网络进行验证,利用测试集的数据进行测试。表3 为期望输出和通过测试集仿真后的实际输出部分数据,可以看出,实验构建的神经网络对齿轮各种故障状态具有较高的识别率。
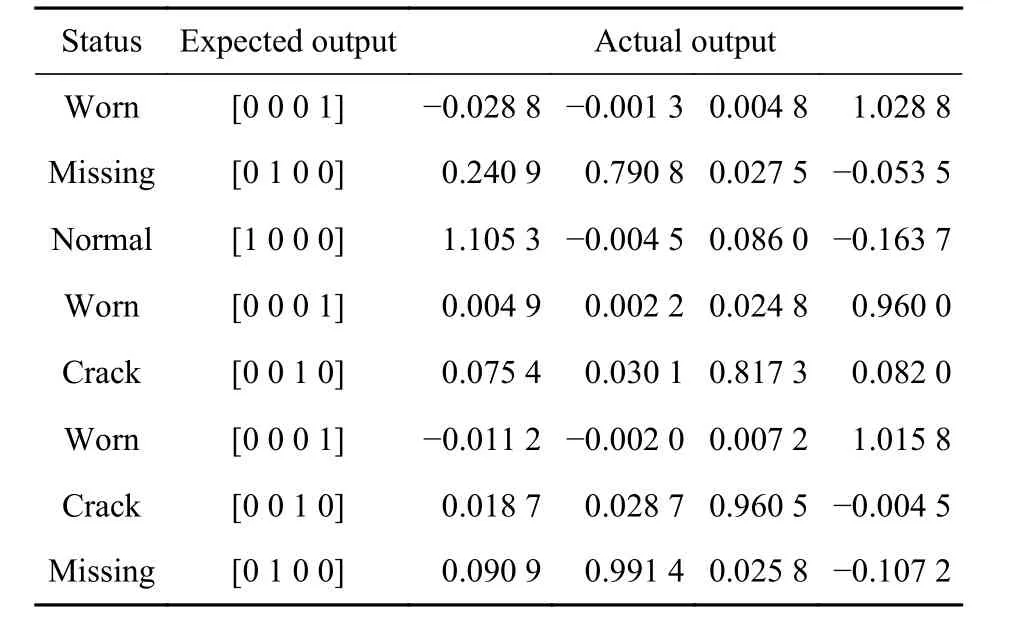
表3 预测输出与实际输出对比Table 3 Comparison table of expected output and actual output
4 结论
1)使用EMD 方法对采集到的信号进行处理,提取出故障信号的若干IMF 分量,此时能够对信号进行比较直观地分析。将提取出的故障特征参数作为BP 神经网络的输入样本进行网络训练和故障模式识别,该方法操作简单,能够识别多数常见故障齿轮。
2)基于EMD 和BP 神经网络的齿轮故障诊断方法,相比于传统的单一BP 神经网络,使其训练误差从原来0.01 左右降低至0.001 左右,训练迭代次数可减小至10 次以内。
