基于跳步的增量式影响力最大化算法

黄 颖，梁春泉，杨泽宽，曹晓旭，武文君

(西北农林科技大学 信息工程学院，陕西 杨陵 712100)

0 引 言

影响力最大化是在线社交网络中的重要问题，对口碑营销、舆情控制等众多应用的实施起着关键性作用[1,2]。给定一个网络和参数k，该问题旨在找出其中k个用户，在某种传播模型下发起信息传播，使得最终受影响用户总数最大化[3,4]。常见传播模型有独立级联和线性阈值模型；在这二者下，影响力最大化问题均为NP-hard[5]。针对该问题，经典算法采用贪心策略、启发式地选择影响力增益最大者作为输出[5]。为提高贪心算法效率，学术界提出两类方法：利用上限值减少评估每个节点影响力的重复次数[6,7]；利用传播局部化特性降低单次评估所需时间[8,9]。

现有算法大多仅处理静态网络，然而在线社交网络天然动态，其中影响力用户会随着网络结构变动而变化[10,11]。部分研究开始解决动态网络中影响力最大化问题[10,12-17]，但并非用来应对网络拓扑结构的变动。为此，文献[11，18]提出了跟踪动态网络中最大影响力节点的算法。然而这些算法应对任何变动都需要重新选择k个节点作为输出，且每选一个节点均需要评估剩下节点的影响力，降低效率。本文同样关注网络结构持续变化下跟踪影响力用户的问题，受文献[8]启发，提出一种基于跳步(hop)的增量式算法。利用影响传播的跳步局部化特点，算法快速识别无需变化的节点，并增量地替换过时节点；最后在真实数据集上实验验证了算法的执行效率。

1 相关技术及问题定义

1.1 影响力最大化问题

社交网络可建模为有向图G=(V,E)， 其中顶点集V表示所有用户，边集E={(u,v)|u∈V,v∈V} 表示用户u与v之间联系。每条边e=(u,v)∈E关联着一个概率值pu,v∈[0,1]， 用来表示信息传播过程中用户u对v的激活概率。对于有向边(u,v)， 称节点v为u的邻居，则Nu={v|(u,v)∈E} 为u邻居集；称u是v的逆邻居，则Rv={v|(u,v)∈E} 为v的逆邻居集。

给定社交网络G和参数k， 影响力最大化问题旨在从网络G中选择种子集S*∈V且|S*|=k， 按照某种传播策略，由S*中的节点开始级联地激活其它节点，使得最终激活节点的期望总数σ(S*) 最大化，如式(1)所示

σ(S*)=Max(σ(S)|S⊆V,|S|=k)

(1)

本研究采用独立级联传播模型，给定一个种子集S∈V， 其传播过程如下：初始化种子集S为激活状态；从S开始，每个新激活节点u有一次机会以概率pu,v激活其尚未激活的每个邻居节点v∈Nu； 传播不断向前推进，直至没有新节点被激活。

在独立级联模型下，影响力最大化问题为NP-hard难题[5]。利用评估函数σ(S) 的子模块性质和边际效应，可设计一个近似比为1-1/e的贪心算法，如算法1所示[5]。算法启发式地选择令影响力增益最大者加入种子集S。

算法1： Greedy(k,σ(·))

输入： 种子集个数k， 评估种子影响力函数σ(·)

输出： 最具影响力种子集S

(1)S←{}

(2) fori=0 tokdo:

(3)u←argmaxu∈VS((σ(S∪{u})-σ(S))

(4)S←S∪{u}

(5) returnS

1.2 基于跳步的独立级联模型

算法1的关键步骤是计算影响力σ(S)， 进而计算增益Δσ(S,u)=σ(S∪{u})-σ(S)， 但不幸的是准确获取σ(S) 是一个#P-hard难题[9]。早期研究通过多次蒙特卡罗模拟获得评估值，时间开销巨大。文献[8]通过实证发现在蒙特卡罗模拟中，大多数激活节点都产生于传播过程中的前几个跳步，特别是传播跳步数h≤2时。因此，为提高效率，文献[8]提出采用h跳步内传播的期望值σh(S)估算σ(S)， 用Δσh(S,u) 估算Δσ(S,u)。 当h≤2时，由于传播路径不存在回路，可以直接通过概率运算获得σh(S) 和Δσh(S,u)。 详细计算过程参见文献[8]。

(2)

向S添加节点u时，影响力增益可用式(3)计算

(3)

(4)

向S加入节点u时，节点v的受影响概率将更新为

(5)

贪心算法所需的影响力增益可用式(6)计算

(6)

1.3 动态网络中的影响力最大化问题

给定t时的网络Gt， 一个包含k种子的集合St， 以及经过Δt的网络变化ΔG，求新网络Gt+Δt=Gt⊕ΔG中影响力最大化种子集St+Δt。 对ΔG，本文仅考虑增边的情况。

本文用到的主要符号见表1。

表1 符号

2 提出的方法

2.1 设计思想

网络拓扑结构的小变化一般情况下不会引起影响力节点的大变动，这是增量式算法能以实现的基础依据[11,18]。对发生变化后的前后两个网络Gt和Gt+1， 增量算法分析ΔGt， 尽可能充分利用Gt的结果St， 快速获得Gt+1对应St+1。

基于上述思路，本文提出一个有限跳步数传播下最具影响力节点的跟踪算法。利用有限跳步局部传播特性，算法通过比较ΔGt涉及节点与St中节点的影响力增益，直接识别出St中无需变动部分，并增量地替换有可能变动部分；二者一起构成St+1。 相对于现有研究[11,18]，本文方法以更直接的方式重复利用St， 无需重新评估和选择每一个影响力节点，因此能更快速获得St+1。

具体地，在任何时刻t，本文算法为图Gt维护h跳步传播下最具影响力节点St={s1,s2,…sk}， 其中节点按入选时的影响力增益降序排序。考虑增边变化会引起部分节点的影响力提升，算法首先识别出该部分节点并更新其影响力上限，其次令St与之比较，识别出St无需变化部分，最后增量式地替换变化部分。

2.2 识别增益上限增加的节点

当网络的Gt拓扑结构发生增边ΔGt={(u,v)} 变化，部分节点可通过在新增边 (u,v) 传播，影响其它节点。然而，由于信息传播局限于h≤2跳步以内，因此仅有节点u及其前驱Rv能够利用 (u,v) 进行传播，进而提升它们影响力的上限。这些节点的查找及其影响力上限的更新方法如算法2所示。

算法2： MaxGainIncNodes(G,(u,v),h)

输入： 网络图G， 边u→v， 跳数h

输出： 影响力有提升的节点集合T

(1)T←{}

(3)T←T∪{u}

(4) ifh== 2 then

(5) foreachw∈Rudo

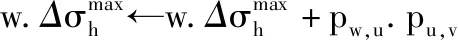
(7)T←T∪{w}

(8) foreachw∈Nvdo

(10) returnT

算法2中，步骤(2)计算节点u在节点v上获得的最大影响力提升，步骤(6)计算u前驱节点在v上获得的提升，步骤(9)计算u在v后继节点上获得的提升；步骤(3) 和步骤(7)则收集影响力有提升的节点。

2.3 识别未发生变化节点

算法3： FindIsrtPos(S,u,k,h)

输入： 最具影响力种子集S， 影响力上限增加的节点u， 种子集个数k， 跳数h

输出： 查找节点最大可能排位left

(1)left←1,right←k

(2) while (left≤right) do

(3)mid←(left+right)/2

(6) else thenright←mid-1

(7) returnleft

2.4 替换新节点

若影响力上限增加的节点u在当前种子集St中找到插入位置pos，则u有可能成为排在pos的种子节点，进而St中排位在pos位置之后的节点，由于受边际效应的影响，实际影响力增益可能会降低，因此需要重新评估节点影响力增益，更新种子集。更新过程如算法4所示。为提高效率算法初始节点实际增益为最大增益(步骤(1))，进而采用CELF算法[6]更新S[pos∶k] 部分的种子(步骤(2)～步骤(7))。

算法4： UpdateSeeds(S,k,h,pos)

输入： 最具影响力种子集S， 种子集个数k， 跳数h， 插入位置pos

输出： 更新后最具影响力种子集S

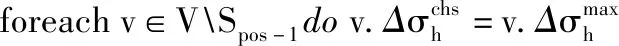
(2) fori=postokdo

(3) foreachv∈VSi-1docurv=false

(4) while true do

(6) ifcurv=truethensi=u*, break

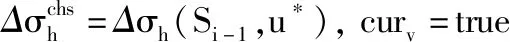
(8) returnS

最后，本文提出的基于跳步的增量式影响力最大算法如算法5所示。算法首先获取影响力上限增加的节点集(步骤(2))，为其中每个节点尝试找到在St中的排位(步骤(4))；若找到，则更新St中排在pos的种子节点。

算法5： IC-HopInc(Gt,St,k,h,(u,v))

输入：t时网络图Gt，t时最具影响力集合St， 种子集合个数k， 跳数h， 边u→v

输出：t+1最具影响力集合St+1

(1)St+1=St

(2)T←MaxGainIncNodes(G,(u,v),h)

(3) foreachw∈Tdo

(4)pos←FindIsrtPos(St+1,w)

(5) ifpos≤kthen

(6)St+1=UpdateSeeds(St+1,k,pos)

(7) returnSt+1

2.5 复杂性分析

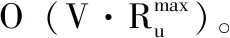
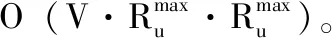
实际上，在网络单位变化情况下，不管是1跳步还是2跳步传播，大多数的非网络节点v∈V-St的影响力上限都不会瞬间增加到让它成为一个可能的种子节点，因此算法5中的步骤(5)很少成立。算法时间运行取决于步骤(2)和步骤(4)。因此，在1跳情况下，对大多数节点，步骤(2)和步骤(4)单位时间即可完成O(1)； 在2跳情况下，步骤(2)需要O(Rmax) 时间，而步骤(4)只需单位时间，结合O(Rmax) 循环，总运行时间仅需O(Rmax)。 下一节实验结果验证了我们算法的高效性。

不论是1跳步传播还是2跳步传播的情况下，IC-HopInc都仅需要O(V) 空间去存储每个节点1跳步或2跳步的传播受影响概率，节点的影响力增益上限，以及节点入选种子集的影响力增益。

3 实验及结果分析

本部分在5个真实数据集上进行实验评估，与最新的跟踪动态网络中最具影响力节点的算法比较，以运行时间为衡量标注，验证本文所提出算法IC-HopInc的高效性。为便于后文讨论，在1跳步传播情况下，命名本文所提出的算法为OneIC-HopInc；在2跳步传播情况下，命名为TwoIC-HopInc；IC-HopInc则表示这二者。

3.1 实验设置

实验中所有评估算法均采用复杂网络处理工具包Networkx(v2.4)(http://networkx.github.io/)和Python(v3.7)编程语言行实现。实验所用计算机的信息为：处理器AMD Ryzen 5 1500X 3.50 GHz，内存16.0 GB，操作系统Windows 10。

数据集：实验数据集来源于斯坦福数据集(http://snap.stanford.edu/)与NewMan个人数据网站(http://www-personal.umich.edu/～mejn/netdata/)。所采用的数据集有海豚社会网络数据集(dolphin)、美国大学橄榄球数据集(football)、维基选票网站数据集(Wiki-vote)、消费者评论网站数据集(soc-Epinions1)和书籍标签推荐数据集(soc-delicious)。表2为具体信息。

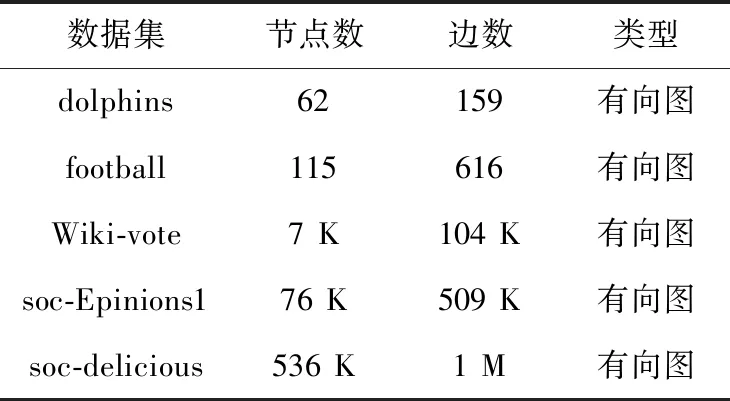
表2 网络数据集

基准算法：实验中，本文提出的OneIC-HopInc和TwoIC-HopInc将与下列基准算法比较：静态OneHop算法、静态TwoHop算法、UBI算法和IncInf算法，简介如下：

(1)OneHop：在1跳步传播下，采用独立级联模型的静态影响力最大化算法[8]；

(2)TwoHop：在2跳步传播下，采用独立级联模型的静态影响力最大化算法[8]；

(3)UBI：一种影响力节点跟踪算法[11]，通过对先前输出St中的节点做k次替换以提升种子集影响力，从而获得当前的输出St+1；

(4)IncInf：另一种影响力节点跟踪算法[18]，利用先前输出St、 节点度最高或节点度变动最高的节点和变化信息，构造候选集并评估其中每个节点影响力增益，从中选择k个增益最高者作为当前输出St+1。

数据预处理：由于上述网络数据集中并未包含传播概率，实验中采用研究界广泛使用的Uniform(UNI) 和Trivalency(TRI)模型设置网络传播概率[8,11]。

(1)Uniform(UNI)：对每条边(u,v)∈E， 设置传播概率为pu,v=0.1。

(2)Trivalency(TRI)：对每条边(u,v)∈E， 设置传播pu,v为{0.1,0.01,0.001}中的一个随机值。

为得到动态图，实验中对网络图进行100次随机加边，取算法响应加边的平均运行时间作为结果输出。

3.2 实验结果及分析

3.2.1 大规模网络对比

本节实验在Wiki-vote、soc-Epinions1、soc-delicious这3个大型数据集上进行，比较算法找出k=1,10,100,1000个最具影响力种子所需时间；网络数据分别设置UNI概率值和TRI概率值。

图1给出了传播概率值设置为UNI时，OneHop算法、OneIC-HopInc算法和IncInf算法运行时间的曲线。图2给出了传播概率值设置为TRI时TwoHop算法、TwoIC-HopInc算法和IncInf算法运行时间的曲线。

从图1和图2可看到，在不同概率值设置下，相同算法的运行时间会出现略微的差别。同时可看到随着需要找出种子数k不断增大，所有算法的运行时间也随之增加。然而，不论是在UNI模型还是在TRI模型下，IC-HopInc算法运行时间均远少于静态算法和动态算法IncInf。在2跳步传播情况下(例如TRI模型下Wiki-vote)本文所提算法运行时间与静态算法较为接近，其原因是在随机加边过程中，边加在当前影响力增益最大的节点上，从而要更新排它之后的所有种子节点，导致了最差运行时间。但即便最差情况下，IC-HopInc算法的运行时间仍在可接受范围内。此外，可看到IncInf算法在网络拓扑结构变化较小时，其运行时间接近于静态算法，原因是需进行大量计算，耗费大量时间。

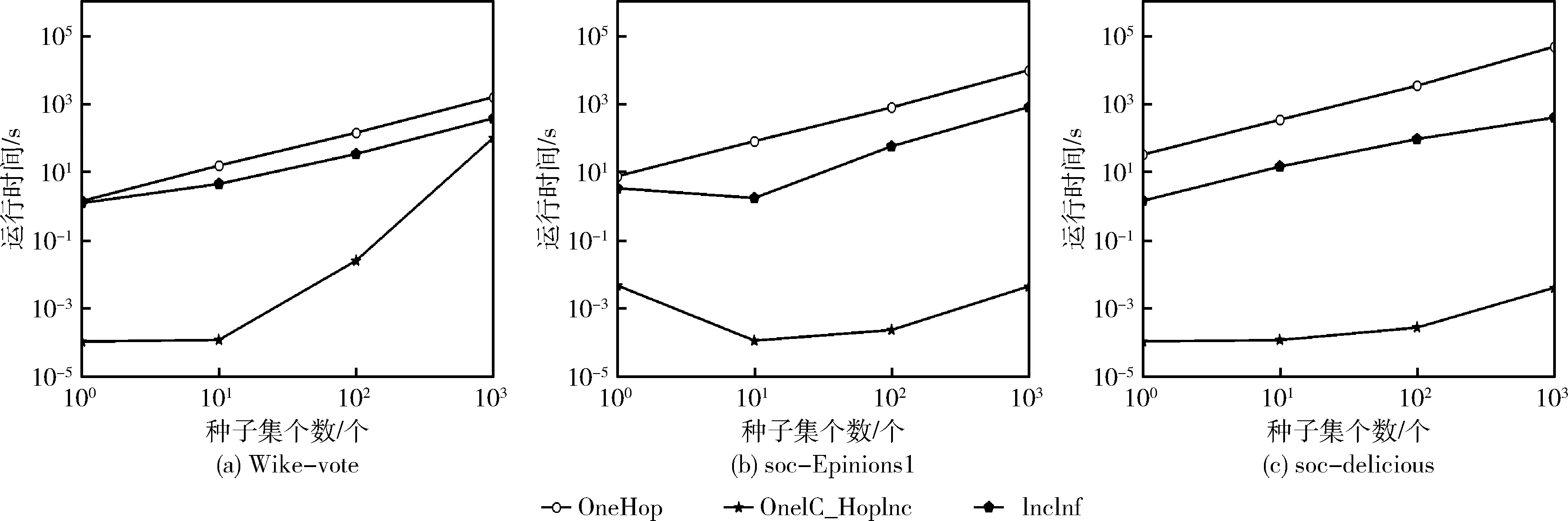
图1 UNI模型下一跳对比

图2 TRI模型下二跳对比

实验中还发现在大多数情况下，很少出现替换影响增益最大节点、且算法最坏的情况，即重新计算所有种子节点的情况，很少出现。综上，本文提出的IC-HopInc算法可有效应对大规模网络拓扑结构变化。

3.2.2 小规模网络对比

本节实验在dolphins、football数据集上进行，比较算法为找到k=1,10,20,30个最大影响力节点所需时间。和上节实验一样，网络数据分别设置UNI概率值和TRI概率值。

图3对比了传播概率值设置为UNI时，TwoHop算法、TwoIC-HopInc算法、IncInf，以及UBI算法的运行时间。图4对比了传播概率值设置为TRI时，OneHop算法、OneIC-HopInc算法、IncInf算法，以及UBI算法的运行时间。

图3 UNI模型下二跳对比

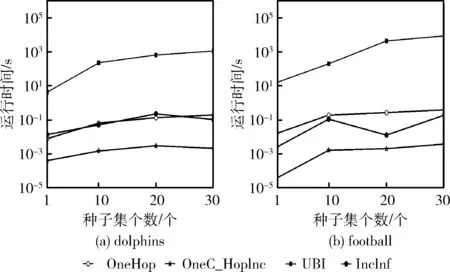
图4 TRI模型下一跳对比

从图3和图4中可以看到在两种概率值模型下，UBI算法所需时间远大于基于跳步的静态算法、HopInc算法以及动态IncInf算法。当需要选择的种子数较小时，HopInc的算法运行最快；二跳范围内，静态算法以及动态IncInf算法加边后重新计算的时间(特别是在种子集大小为20和30时)与HopInc算法运行时间差别不大，前者原因在于，二跳情况下，HopInc算法在确定受影响范围内受增益最大的节点浪费了时间或者在替换过程中遇到最坏情况所造成。后者原因在于拓扑变化过小，节点的选择类似静态贪心算法。对比之前在大规模网络下的运行情况来说，即使出现最差的运行情况，算法的效果也是较优于对比算法，其运行时间还是在可接受的范围内。

UBI算法采用节点追踪实现节点替换，但在选择替换节点时，需要进行 |V-S| 次的影响评估，并且需要不断的去维护概率矩阵，相比于本文的算法，需要进行大量的计算。经过测试，即使在仅含1000个节点的小图上，UBI算法在种子集的选择中运行200多个小时仍然无法得到结果，因此本节选择了在数据量较小的dolphins和football数据集进行实验，对比不同算法运行时间。

综上实验结果和分析，无论是在大规模还是小规模网络上，HopInc算法运行时间均少于UBI和IncInf动态跟踪算法，也少于基于跳步传播的静态影响力最大化算法算法，验证了HopInc算法的高效性。

4 结束语

本文提出了一个基于跳步传播的增量式影响力最大化算法，即HopInc。该算法利用有限跳步传播特点，快速评估网络变化所涉及节点的影响力增益上限，与先前输出结果比较，识别无需变动的结果；同时快速更新有可能需要变动的影响力节点。在多个真实数据集上的实验结果表明，相比静态算法和其它最新的动态跟踪算法，HopInc算法能以更快速度找到动态网络中最具影响力节点。