港航多视角下内河集装箱船舶配载决策
2021-01-20张煜,李俊,徐进,李斌
张 煜,李 俊,徐 进,李 斌
(1.武汉理工大学 港口物流技术与装备教育部工程研究中心,湖北 武汉 430063;2.武汉科技大学 汽车与交通工程学院,湖北 武汉 430081;3.武汉理工大学 物流工程学院,湖北 武汉 430063;4.福建工程学院 交通运输学院,福建 福州 350108)
0 引 言
集装箱运输作为水上货物运输的主要方式之一,以其高效率、高质量、高密集、高标准化等特点取得了快速发展,其涉及的船舶配载问题也得到了国内外学者的广泛关注。
已有相关研究主要围绕海上集装箱运输展开,多采用分阶段方法进行研究,将集装箱船舶配载划分为主贝计划问题(master bay planning problem, MBPP)和贝内计划问题(slot planning problem, SPP)。对于MBPP,Tierney等[1]验证了最小化舱盖板压箱数量的集装箱船舶配载问题是NP难问题。Ambrosino等[2,3]将MBPP拓展为全航线主贝计划问题,提出了混合整数规划模型和启发式方法实现问题求解。对于SPP,Parreo等[4]提出了整数规划模型,并设计了贪婪随机自适应随机搜索方法求解。李俊等[5]综合考虑堆场发箱与SPP研究装船排序问题,设计吱呀轮-混合演算策略两阶段算法求解。田维[6]分析不确定事件对配载计划的影响,构建不确定集港环境下的装箱排序模型。Kroer等[7]研究了船舶单贝位内的堆箱和重排箱问题,提出了基于二元决策图和DPLL求解器的求解方法。
此外,祝慧灵等[8]针对全航线配载问题构建了多目标优化模型,并基于遗传算法开发优化算法开展仿真实验。Ambrosino等[9]构建混合整数规划模型,并以MIP Solver进行验证。李俊等[10]考虑内河运输中集装箱重量不确定因素影响,构建随机规划模型,并设计混合领域搜索算法求解。
综上所述,现阶段集装箱配载问题主要关注集装箱海洋运输,少有学者关注其内河运输问题。随着内河运输业的发展,如何高效、经济地提高内河集装箱运输收益有待研究。因此,本文考虑内河集装箱运输特性,从港航多视角出发对内河集装箱船舶配载决策方法,保障港航双方利益。
1 问题描述
在实际的港口集装箱营运中,集装箱船的配载从预配到集装箱实际装载涉及船方、港方和口岸管理等各个环节,主要实现预配图、实配图及积载图三图的制定。其中,集装箱预配也可称为主贝计划问题(MBPP),是集装箱配载的第一步,也是至关重要的一个环节,在编制主贝计划配载方案时必须考虑船舶和货物的安全性。
船舶预配载是船公司的预配中心根据船舶航次订舱情况,确定集装箱在船舱的最优位置,以满足船舶积载强度、纵向强度、堆积等要求,最大限度利用船舶存储空间,尽力满足船舶快速装卸要求,避免倒箱操作,保证船舶和货物的安全性。
为满足集装箱船舶航线配载决策需求,本文主要研究多港主贝计划问题,解决各挂靠港集装箱预配载问题,如图1所示。
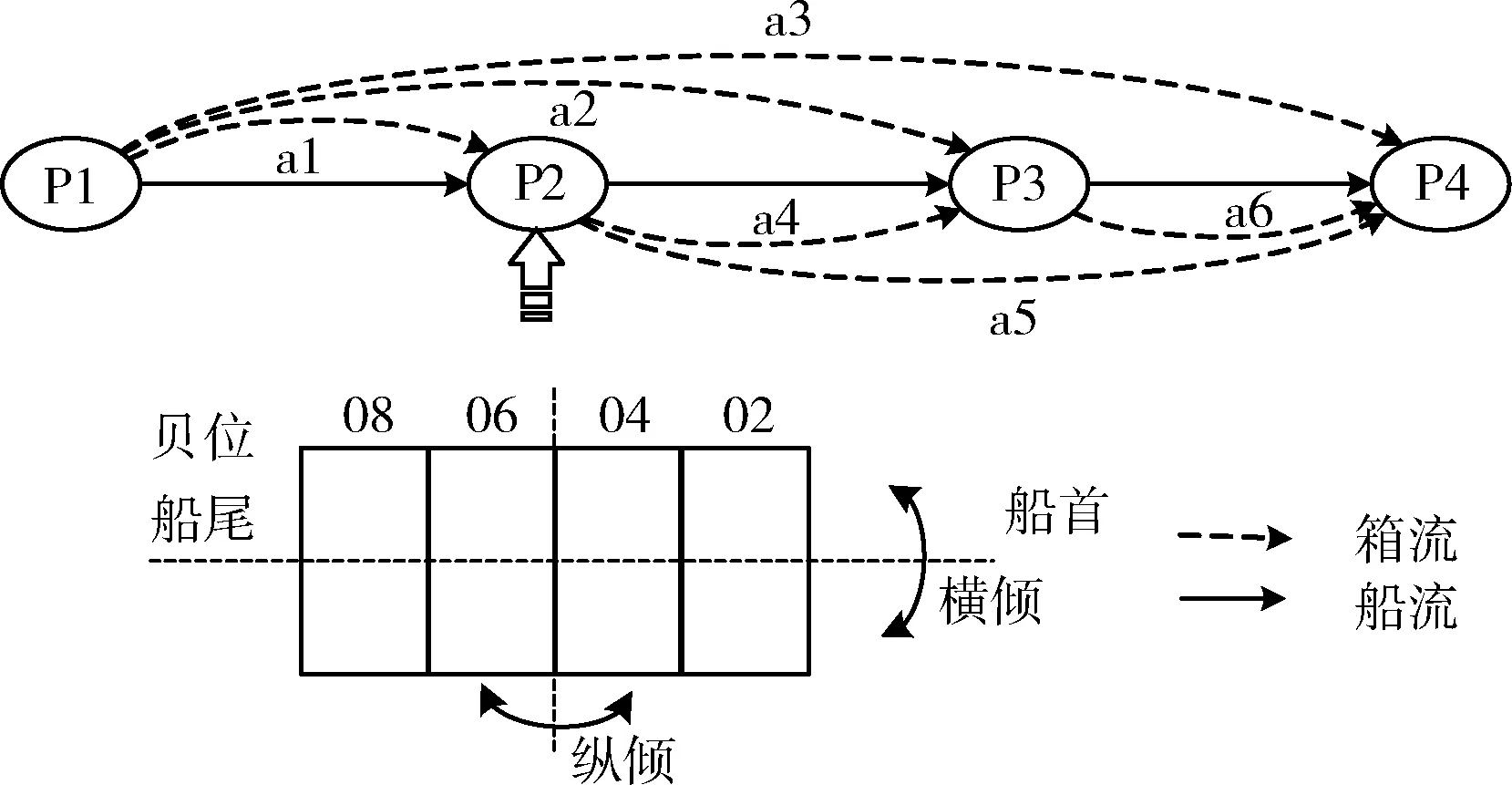
图1 内河集装箱船舶航线配载
从图1中可以看出,在航线运输过程中,船舶顺序遍历各挂靠港,并依次进行集装箱配载作业。在制定各港口配载计划时,考虑当前港口的集装箱信息(尺寸、重量等级、目的港、数量等),将待装船集装箱集合有效划分并分配到船舶各个贝位内,以满足船舶稳性、强度、容量等约束,避免翻倒箱,提高船舶装载率。
此外,在实际内河集装箱运输作业中,船舶船体小、运输能力有限、船舶装载要求高,船方制定预配载计划时忽视港方利益,往往会造成其装船作业时大量翻箱、不同岸桥装卸作业不均衡等问题,影响码头生产作业效率。港方为提高码头装卸作业效率对预配载计划做出较大调整时,往往也容易导致船舶内翻倒箱产生,破坏船舶稳定性,影响其航行安全。因此,在船舶配载决策时,如何从港航多视角出发,制定综合考虑双方利益的配载计划在内河集装箱运输中至关重要。
2 模型构建
2.1 基本假设
(1)内河集装箱船均由散货船改装而来,无舱盖板,各贝物理结构均为方形;
(2)由于内河航线的去程和回程存在货流不平衡现象,不失一般性,模型构建仅考虑去程;
(3)各挂靠港出口集装箱信息已知,且不变;
(4)仅考虑具有同一尺寸的20ft标准箱;
(5)岸桥装、卸一个集装箱的时间相同,不考虑装卸箱的等待时间,以装卸箱量的差异描述岸桥作业时间差;
(6)在任意港口集装箱均可全部装船,不存在集装箱选择问题。
2.2 参数及变量设计
(1)参数定义:

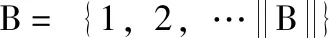

nic表示在i挂靠港岸桥c作业节点;
Bc(i)={bni(c-1),…,bnic} 表示岸桥c作业区间为贝位ni(c-1)至贝位nic;
BP,BA分别表示船舶前半部、船舶后半部贝位的集合;
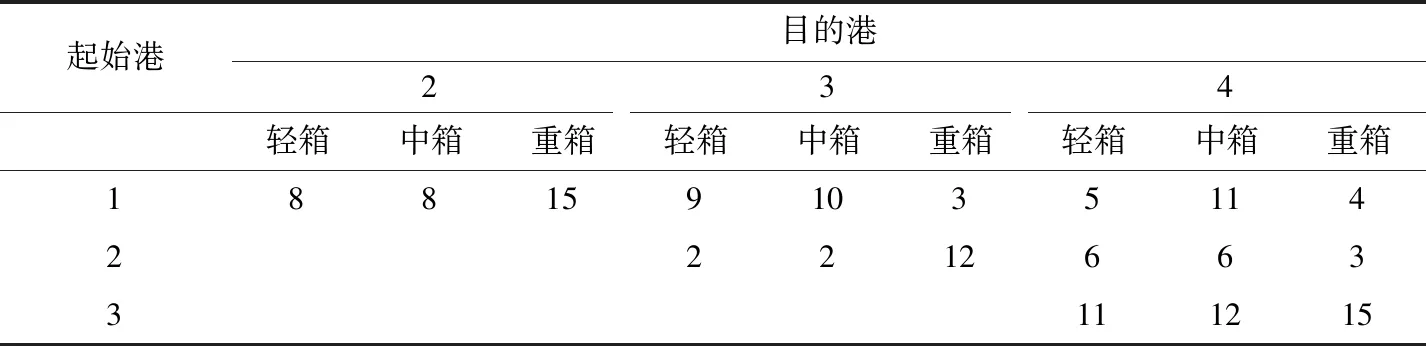
Pt(i),Ps(i),P(i) 为航线上港口i对应的O-D副集合,Pt(i)={a|o,i,d∈H,o D表示不同a流向集装箱所对应的目的港集合,D={d|a=(o,d),a∈P(i)}; G={1,2,3} 表示集装箱重量等级集合,分为轻、中、重3个重量等级,g=1表示轻箱(均重:7吨),g=2表示中箱(均重:14吨),g=3表示重箱(均重:21吨); Ng表示a流向下重量等级为g的集装箱数量,a∈Ps(i) (单位:TEU); wg表示g重量等级集装箱的平均箱重(单位:吨); CTeub,CTonb分别表示船舶b贝位的最大舱容(单位:TEU)、最大载重(单位:吨); (2)决策变量定义: tic表示在i挂靠港岸桥c的装卸作业量; xbg(a) 表示港口副流向a分配到船舶贝位b中的g重量等级集装箱数量; yb(i) 为0-1变量。若在挂靠港i船舶贝位b被占用,则为1;否则为0; zb(a) 为0-1变量。若在i挂靠港a流向下的集装箱占据了船舶贝位b, 则为1;否则为0; ebj(i) 为0-1变量。若在i挂靠港贝位b被j目的港集装箱占用,则为1;否则为0。 港航多视角下的船舶配载决策模型需要综合考虑港方和船方利益偏好,模型构建如下: (1)目标函数 f=min(f1,f2,f3) (1) f1=∑i∈H∑b∈Byb(i) (2) f2=∑i∈H∑b∈Bsign(∑j∈Hebj(i)-yb(i)) (3) f3=max|tic-tie|, ∀i∈H,c,e∈Y(i) (4) (2)约束条件 ∑b∈Bxbg(a)=Ng(a),∀i∈H,a∈Ps(i),g∈G (5) ∑a∈P(i)∑g∈Gxbg(a)≤CTeub,∀i∈H,b∈B (6) ∑a∈P(i)∑g∈Gwgxbg(a)≤CTonb,∀i∈H,b∈B (7) (8) tic=∑b∈Bc(i)(∑a∈Ps(i),g∈Gxbg(a)+ (9) zb(a)≤∑g∈Gxbg(a)≤Mzb(a),∀i∈H,a∈P(i),b∈B (10) yb(i)≤∑a∈P(i)zb(a)≤Myb(i),∀i∈H,b∈B (11) ebj(i)≤∑a∈P(i)zb(a)(D(a)≡j)≤Mebj(i) (12) nic-ni(c-1)≥3,∀i∈H,c∈Y(i) (13) tic≥0,∀i∈H,c∈Y(i) (14) xbg(a)≥0,∀i∈H,a∈P(i),b∈B,g∈G (15) yb(i)∈{0,1},∀i∈H,b∈B (16) zb(a)∈{0,1},∀i∈H,a∈P(i),b∈B (17) ebj(i)∈{0,1},i,j∈H,i (18) 其中,式(1)~式(4)表示目标函数。f表示模型优化目标,通过最小化船舶贝位占用(f1)、不同目的港集装箱混装贝位数量(f2)、不同岸桥装卸作业量之差(f3),保障港航利益。式(5)~式(18)表示约束条件,其中式(5)保证所有集装箱均能装船,式(6)、式(7)保证贝内装载集装箱不超过其舱容及载重限制;式(8)表示船舶航行安全性约束,通过限制船舶纵倾,保证集装箱运输的安全性;式(9)描述岸桥装卸作业量计算方式;式(10)~式(12)表示决策变量yb(i)、zb(a)、xbg(a)、ebj(i) 之间的关系,若yb(i)=1, 在i港口b贝位被占用,则在i港口b贝位中存在O-D流向集装箱,即∑a∈P(i)zb(a)≥1, 若yb(i)=0, 贝位不装载集装箱,此时∑a∈P(i)zb(a)=0, 则决策变量yb(i) 和zb(a) 存在如式(11)所示关系;式(13)表示岸桥至少作业3个连续贝位,保证岸桥充分利用的同时,保障同步作业安全间距;式(14)~式(18)定义决策变量。 港航多视角下的船舶配载决策需要多目标优化,难以在有效时间内直接使用例如Cplex、Gurobi等软件实现模型精确求解,需要设计更为有效的多目标寻优算法。本文以禁忌搜索算法框架为主,以模糊关联熵系数引导搜索的方向,通过启发式规则加快解搜索速率,实现港航多视角下内河船舶配载多目标优化。算法流程如图2所示。具体搜索流程如下。 图2 启发式算法搜索流程 步骤1 理想解及子目标上下界确定:对模型中的各子目标分别采用Gurobi多次运行求解,取平均值的λ倍 (λ∈(0,1)) 作为子目标下界,多次求解后各子目标的最大值为上界,最优值为其理想解,进入步骤2; 步骤2 变量初始化:初始化迭代次数Iterations=1, 分散搜索执行次数L1=0, 禁忌表Tabu_List=∅, 最优解BS=∅, 当前解CS=∅, 进入步骤3; 步骤3 个体生成:根据编码结构随机生成个体,进入步骤4; 步骤4 个体解码:根据个体编码确定各贝装载优先级,以启发式规则进行集装箱分配,通过纵倾优化策略对初始配载方案进行优化,产生满足约束的可行解,计算不同配载方案适应度函数,选择最优的N个配载方案构造个体候选解集C(sol), 进入步骤5; 步骤5 最优候选解评估:评估各候选集解的适应度函数值,选择最优的候选解S*, 进入步骤6; 步骤6 数据更新:判断S*的适应度函数值是否优于BS, 若是更新BS与CS为S*, 更新禁忌表,进入步骤8;否则,进入步骤7; 步骤7 数据更新:判断S*是否在禁忌表中,若是,进入步骤10。否则,更新CS为S*, 更新禁忌表及Pareto解集,进入步骤8; 步骤8 拥挤算子选择排序:判断Pareto解集长度是否大于某一个值,若是,基于非支配解排序及拥挤度计算,进行个体选择,更新Pareto解集,并进入步骤9;否则直接进入步骤9; 步骤9 终止判断:判断是否分散搜索执行次数L1≥max_Iterations或最优解值优于理想解,若是终止搜索,进入步骤10;否则,L1=L1+1, 进入步骤3; 步骤10 输出结果:输出Pareto解集,输出最优解BS及最优解值。 个体采用分段实数编码的形式进行组织,个体按航线挂靠港口分为多段,每段按船舶贝集合分为多个位点,如图3所示。其中,位点值Xib表示i港口b贝位的优先级,启发式算法通过贝位优先级控制集装箱的装载,实现配载问题的求解。 图3 个体编码设计 个体解码过程包括两个阶段:启发式规则装箱阶段及优化阶段。其中,在装箱阶段集装箱装载即按港口遍历顺序,在满足船舶舱容和载重的要求下,依次确定集装箱的装载位置,得到船舶初始装载状态;优化阶段即基于船舶初始装载状态调整集装箱的装载位置,对目标和船舶安全进行调整,得到最终的配载方案。 个体解码具体实施步骤如下: (1)第一阶段:启发式规则装箱,生成初始配载方案 步骤3 在同类箱组p(p∈P) 中选择目标箱inp, 初始化inp=1, 进入步骤4; 步骤4 判断是否inp≤N(p), 若是,进入步骤5;否则,令p=p+1, 进入步骤2; 步骤5 判断是否满足装载要求,若是,令inp=inp+1, 更新贝位b的当前装箱量与载重,进入步骤4。否则,进入步骤2; (2)第二阶段:优化阶段,优化船舶纵倾,产生个体候选集 首先,确定纵倾优化策略[11],如下: 策略1:互换贝内装载集装箱信息,快速优化船舶纵倾力矩。在一定迭代范围内,进行贝位的随机选择与交换,快速调整船舶纵倾。 策略2:互换不同贝位箱组所在位置,进一步优化船舶纵倾力矩。当策略1无法优化船舶纵倾时,继续使用策略2对船舶纵倾力矩进行调整。调整方式是:在一定迭代范围内,随机选择贝位及符合贝位容量与载重的箱组进行互换,优化纵倾力矩。 策略3:不同贝位箱组拆分重组,进一步优化船舶纵倾力矩。当策略2无法对船舶纵倾进行优化时,继续采用策略3优化纵倾。选择同一流向或者空贝位进行拆分,重新分配集装箱,调整纵倾。 再按如下流程完成优化部分的搜索: 步骤6 计算当前港口船舶纵倾力矩Gc, 初始化迭代次数iter,iteration, 进入步骤7; 步骤7 判断是否0 步骤8 按优化策略优化船舶纵倾,当船舶装载状态满足0 步骤9 判断是否iter 近年来贺利军等[11,12]针对现有优化方法在求解多目标问题上的弊端,将模糊关联熵理论应用于多目标优化中,且验证效果良好。因此,本文引入模糊关联熵理论,将模糊关联熵系数作为启发式算法适应度值,引导Pareto解向理想解靠近,从而消除目标数量级和量纲的影响,避免目标权重选取的主观性。 算例根据“川江及三峡库区运输船舶标准船型主尺度系列”选取集装箱船舶,分别对应内河运输中的小型、大型集装箱,其装载参数见表1。 表1 集装箱船装载参数 根据长江干线集装箱运输主要航线选择挂靠港口数依次为3、4、6的航线见表2。 表2 长江干线集装箱运输航线 考虑到内河集装箱船舶船体小、单次运输箱量有限,以船舶装载率表征装箱数量的不同规模,案例设置50%、70%、90%这3种装载率,分别标记为O50、O70、O90。并设置轻、中、重箱比率为3∶4∶3,描述不同装箱规模下各类集装箱的装箱数量。各船型装载数据及不同装载率下的载重率计算见表3。 表3 箱配载相关信息 根据船型S、航线L、船舶装载率O、箱型比率C构建集装箱运输场景,并以S-L-O-C组合标识。运输场景中的装箱矩阵由excel随机产生,例“S2-L4-O50-C”表示该案例以编号为S2的船舶(该船型相关参数见表1)为配载基础,航线依次挂靠4个港口,在各挂靠港中船舶装载率为50%。此外,为简化模型,设定航线中各挂靠港以两台岸桥同时装卸集装箱,优化港方视角的配载。 以船型S1、航线L4为全航线配载基础,设船舶离开挂靠港时的装载率分别为50%,构建集装箱运输场景。以excel生成集装箱运输场景下的随机案例(见表4)对模型与算法进行仿真分析。 表4 集装箱装载信息 以随机案例求解过程为例研究各子目标的变化趋势绘制图4,可以看出模糊关联熵系数变化明显,收敛性良好;随着模糊关联熵系数收敛,各子目标值出现小范围波动,但整体呈下降趋势,表明多目标问题优化实质是各子目标间相互权衡协调的过程。 图4 目标变化趋势 为进一步验证模型与算法的可行性,绘制随机案例配载结果如图5所示。图中数据显示,所以集装箱均能装船,各贝装载结果满足舱容、载重约束,满足船舶适航性要求。配载结果不存在不同目的港混装情况,贝位平均利用率约为76%,岸桥在各挂靠港的装卸作业量之差最大为1。 图5 随机案例配载数据 以上结果表明提出的模型与算法可行,产生配载方案能够保证岸桥的有效利用,缩短船舶靠泊时间,提高船舶存储空间的利用率,符合港航双方对配载计划的要求。 分别以Gurobi内置分支定界算法和启发式算法对运输场景中的随机案例进行求解运算,记录仿真实验结果见表5。针对Gurobi的求解,本文以启发式算法获得f2,f3值作为上界,启发式算法中采用的子目标下界为f2,f3的下界,构造关于子目标f2与f3的约束,优化子目标f1,求解各案例的最优解。 表5中的数据显示,在小规模运输场景中精确算法求解子目标与启发式算法获得解相差不大,但随着运输场景规模的增大,精确算法求解质量出现明显下降,甚至在半小时内无法求解较大船型、较高装载率的运输场景。因此,启发式算法求解内河集装箱船全航线配载问题有效。 表5 18组算例仿真结果 本文从港航多视角出发研究内河集装箱船舶配载决策问题,构建了考虑港航双方利益的船舶配载优化模型,并设计启发式算法实现问题求解。最后结合长江真实运输场景设计多组仿真算例,开展算例研究。仿真结果表明,本文提出的模型和算法可在提高船舶存储空间利用率的同时,保证码头装卸作业的效率,提高内河集装箱船营运经济性。后续研究将针对内河集装箱船舶航线配载决策多目标优化算法进一步展开。
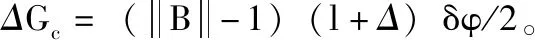
2.3 数学模型
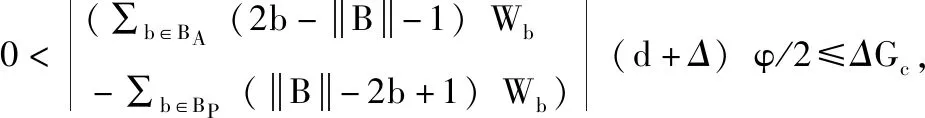
∑a∈P(i-1)-Pt(i),g∈Gxbg(a)),∀i∈H,c∈Y(i)
∀i,j∈H,i3 启发式算法设计
3.1 算法描述

3.2 个体编码

3.3 个体解码


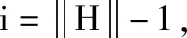
3.4 适应度函数
4 算例研究
4.1 算例设计



4.2 可行性验证


4.3 有效性验证

5 结束语
