基于正交字典的全反馈信道函数估计
2021-01-20孙景锋李德识
孙景锋,李德识
(武汉大学 电子信息学院,湖北 武汉 430072)
0 引 言
传统信道函数估计方法没有利用信道的稀疏特性,存在复杂高、计算量大、实时性差等问题[1]。随着压缩感知理论的发展,基追踪算法、匹配追踪算法(matching pursuit,MP)、正交匹配追踪算法(orthogonal matching pursuit,OMP)等[2,3]被运用到信道估计中。相比均衡算法,匹配算法忽略了部分权重较小的分量,以提高算法的实时性[4]。基追踪算法通过梯度下降方法迭代计算信道函数,存在收敛速度慢的问题[5]。MP算法采用贪婪算法,存在局部最优解的问题。OMP算法通过残差正交投影方法来获得最优匹配结果,存在噪声敏感的问题[6]。广义正交匹配算法(generalized orthogonal matching pursuit,GOMP)在每一次迭代时选择与残差乘积最大的几个字典,但在迭代过程中可能会选择出错误原子[7]。压缩采样匹配追踪(compressive sampling matching pursuit,CoSaMP)[8]和子空间追踪(subspace pursuit,SP)[9]的出现引入了字典回溯的思想,采取先添加原子再进行可靠性筛选的原子选择方法提高重构质量。将压缩感知和均衡算法相结合,可提高收敛速度,但在低信噪比情况下均衡类算法计算误差较大。因此需要研究抗干扰能力强且实时性强的信道估计方法,本文根据匹配信道参数估计推导获取理想信道参数估计的条件;设计训练序列与水声信道函数分量卷积后,构成具备抗干扰能力的正交字典集,在匹配追踪算法框架下能够获取理想信道函数估计结果。信道函数估计流程如图1所示,本文的主要工作和贡献如下:

图1 基于正交字典的全反馈信道函数估计流程
(1)推导计算理想信道参数的训练序列属性,得到数字高斯序列与水声信道函数分量卷积可构造具有自相关特性、正交性和抗干扰能力的字典集。正交字典集与匹配算法相结合,可滤除其它多径和噪声的干扰,提高算法的准确率,减小计算量。
(2)提出一种全反馈结构的水声稀疏信道函数估计算法,验证该结构可矫正数字高斯训练序列不正交造成的系统误差,通过反馈迭代可有效滤除。
1 水声信道模型
由于声信号在水下存在严重的传播损失,反射次数多的传播路径能量损失更严重。传播路径存在以下4种情形:直达路径、海面反射路径、海底反射路径、海面-海底反射路径。图2给出了浅海水声通信传播路径的示意。
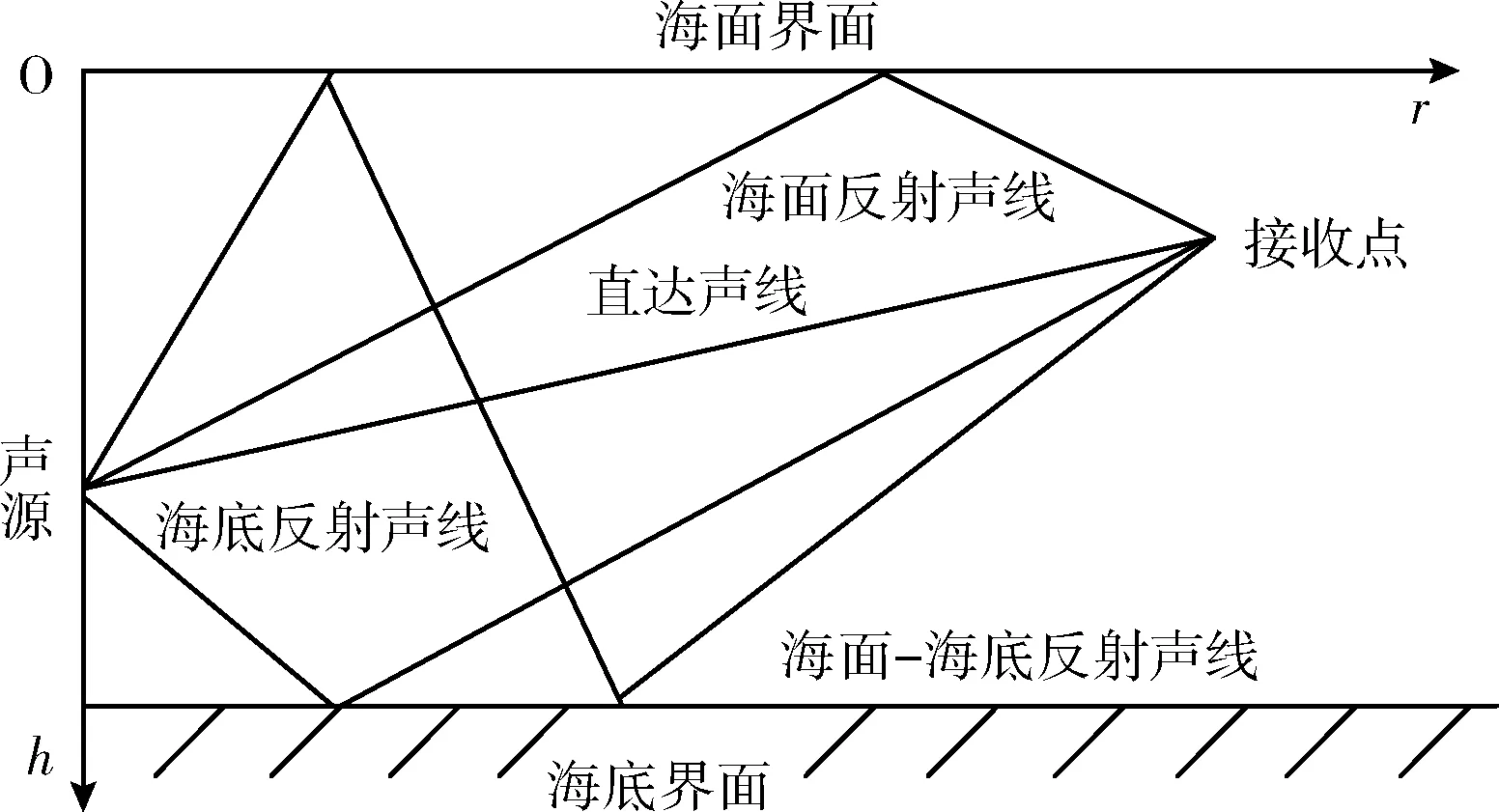
图2 浅海水声通信传播路径
若信号传播路径信息已知,可进一步估计信道传播函数。由于信道模型中的多径时延nk和传播衰减ak是由水下环境和声传播特性共同确定,采用水声环境建模确定信道参数的方法计算复杂度高且受时空因素影响较大,因此可通过匹配算法模型计算得到信道函数参数。为了提高信道函数估计算法的实时性,可利用信道稀疏特性降低求解信道函数的计算复杂度。
基带信号x[n] 经过信道传播后,由于多径效应、传播能量衰减ak和环境噪声干扰noise[n], 接收端信号r[n] 可表示为
r[n]=x[n]⊗h[n]+noise[n]
(1)
在多径传输情况下,r[n] 也可表示为多径信号的叠加和
(2)
其中,h为信道函数,noise为高斯白噪声,M为传播路径的数量。由式(2)可知,信道函数h的冲击响应函数可表示为
(3)
其中,第k条径的传播衰减为ak,传播时延为nk。
2 正交字典构造
在接收端,接收到的信号是多个多径信号的叠加,其中,每一条传播路径的信道函数可表示为
H0=[1,0…0],H1=[0,1…0]…HM-1=[0,0…1]
(4)
由H0,H1…HM-1进行线性组合,可以表达真实的信道函数h[n]。 由式(3)、式(4)可知
h[n]=a0H0+a1H1+…+aM-1HM-1
(5)
接收端的信号分量可以表示为
r0=x⊗H0,r1=x⊗H1…rM-1=x⊗HM-1
(6)
由式(2)可以得到
r=a0r0+a1r1+…+aM-1rM-1+noise
(7)
其中,r为r0,r1…rM-1的线性组合,且每一条传播路径具备相同的结构形式,将式(7)转换成矩阵相乘形式:r=[r0,r1…rM-1][a0,a1...aM-1]T, 结合水声信道稀疏的特点,信道参数a0,a1…aM-1中只有小部分存在数值,故r也可以由r0,r1…rM-1稀疏的表示,因此r0,r1…rM-1为r的字典集。
通过计算r中包含的字典元素的权重来估计信道函数参数。通过计算分析最优信道参数的估计条件,进而获取字典集的正交、抗干扰能力强和自相关峰突出等特性。字典集由训练序列x和信道函数分量Hi卷积生成,由式(4)可知,不同信道环境下的信道函数分量的规律稳定,因此本文通过设计一段特定的训练序列x, 使得x与不同的水声信道函数分量卷积都具备字典集的3点特性。对选用的训练序列进行整数化以适应通信系统,并对整数化后的序列进行性能分析,是否还满足最优条件。
2.1 最优信道参数估计条件
在匹配算法的框架下,任选信道函数的一个参数计算过程进行分析,并从中推导最优信道参数估计条件。信道函数传播衰减参数ai的估计公式为
(8)
其中,
r[n]=a0r0+a1r1+…+aM-1rM-1+noise[n]
带入上式则有
(9)
由于信道参数ai理想的表达式是
(10)
当式(9)可转换成式(10)时,估计结果就可以转换成为真实值,可知式(9)中的ajrj和noise[n] 为干扰项。当字典集满足下列条件时:
(1)
(2)
式(9)可转换为
将条件(1)、条件(2)带入上式,可知能将a′i转换成为真实信道参数ai。 本文通过设计特定的字典集,使得字典元素 {r0,r1…rM-1} 具备正交性和抗干扰能力,可在匹配运算时去除内部干扰和外部干扰,可得到式(10)即理想结果。
字典集可转换成训练序列与信道函数的卷积形式,因此可由字典集性能得知训练序列x具备以下几点性质:
性质1x⊗Hk与x⊗Hl正交,其中k,l∈[0,1…M-1], 且k≠l;
性质2 匹配过程中抗干扰能力强,x⊗Hk+noisek与x⊗Hl+noisel的点积不受noisek,noisel的影响,即 (x⊗Hk+noisek).*(x⊗Hl+noisel)≈(x⊗Hk).*(x⊗Hl),k,l∈[0,1…M-1];
性质3 自相关特性,即 (x⊗Hk).*(x⊗Hk)≫(x⊗Hk).*(x⊗Hl)。
其中a.*b为a与b点积运算,⊗为卷积运算。
2.2 训练序列构造
目前常用的训练码元有:伪随机序列(M序列)、巴克码、随机序列、高斯整数零相关区(Gaussian integer zero correlation zone,ZCZ)序列集[10,11]等。研究发现,高斯序列满足上述性质要求,因此本算法运用数字化的高斯序列作为训练序列,以下验证了高斯序列符合最优解的设计要求。高斯序列在任意两个不同时刻上的随机变量,不仅是互不相关,而且统计独立。选定高斯序列Gau[n], 干扰噪声noise[n], 高斯序列的性质有:
(1)Gau[n-nl].*Gau[n-nk]=0, 其中l≠k;
(2)Gau[n].*noise[n]=0, 与其它噪声不相干;
(3)Gau[n].*Gau[n]=N/2, 其中N为高斯序列功率。
由上面性质推导训练序列的性质:
(1)正交性:rk=Gau[n]⊗Hk=Gau[n-nk],rl=Gau[n]⊗Hl=Gau[n-nl], 可知有不同的字典元素rk,rl, 其中l≠k, 对于他们的点积有
rk.*rl=Gau[n-nk].*Gau[n-nl]=0
(11)
(2)抗干扰能力
r.*rk={Gau[n]⊗H+noise}.*rk=
{Gau[n]⊗H}.*rk
(12)
(3)自相关特性:任一字典元素rk=Gau[n]⊗Hk=Gau[n-nk], 有
rk.*rk=N/2(N为序列的功率)
(13)
由此,可证明高斯序列满足正交字典的基本要求。但高斯序列作为码元序列存在幅值多样、分布随机等缺点,为减小通信系统复杂度,适应通信基带码元要求,则需要将高斯序列转化为整数高斯序列。待转换的序列Gau[n]=[x0,x1…xn-1], 整数目标集合Symbol=[…-3,-2,-1,1,2,3…], 数字化过程即将Gau[n] 中的值映射到Symbol中。数字化的要求是转换后的序列在上述3点性质要求上尽量逼近高斯序列。
高斯序列数字化的方法,常见方法有取整法、聚类法等。取整方法设定阈值后向上或向下取整具备算法简单的优势;聚类方法先将特性相同的点聚集在一起,再将每一块数据分别同值整数化,相比取整虽然操作复杂,但其利用欧式距离对这些点进行分类,能获取最小均方误差,相比取整的方法,聚类法能将特性相近的一些点聚类在一起。因此本文选用聚类的方法作为本文的整数化方法,其中典型的方法为K-means聚类[12]。
首先可以利用欧氏距离将高斯序列分成K块,再将这K块区域的幅值进行同值数字化,K-means聚类算法,其步骤如下:
(1)随机选取K个初始质心;
(2)计算所有样本点到K个质心的距离;
(3)若样本离质心Si最近,那么该样本属于Si点群;若样本点到多个质心的距离相等,则该样本点可被划分到任意组中;
(4)所有样本分组后,计算每个组的样本点均值,将计算的均值作为新的质心;
(5)重复步骤(2)~步骤(4)直到质心收敛算法结束。
由上述方法可以得到K块数据,在Symbol=[…-3,-2,-1,1,2,3…] 中对称的选取K个值,将K块数据中的值对应映射,即完成数字化。图3即为四值数字化的聚类结果。

图3 高斯序列K-means聚类结果
数字化方法可通过数字化后序列的正交性、抗干扰能力、自相关特性等进行评价,为此分别设置了3个指标进行衡量量化的性能。
2.3 训练序列的性能分析
为了对所构造的训练序列进行分析与评价,分别设计了正交偏离角、有无干扰项匹配偏差、相关峰值与最大干扰峰值比来分别对正交性、抗干扰能力、自相关特性进行量化表征。
自相关特性,将相关峰与最大干扰峰值比定义为ratepeak-max-interference, 简化为ratePMI其定义式表达如下
(14)
正交性能分析,通过计算不同码元间的夹角与直角的偏角,并求和表示为正交偏角(declination,OP),其定义式如下
(15)
抗干扰能力分析,抗干扰能力(anti-interference ability,Anti-IA)则是通过对比有无噪声情况下的匹配困难度,有噪声干扰时记为ratenoise, 无噪声干扰时记为ratesign, 抗干扰能力数值越接近1表示码元序列抗噪能力越强,其定义如下
(16)
巴克码在长度12 000内的最长序列为13,对于一般海洋水声通信中,多径的最大时延超过100 ms,要求的训练码元长度超过200,故巴克码不适合作为训练码元。ZCZ序列通过计算产生零相关序列适合作同步码,对于长序列的训练序列会产生更多码值,不适合做基础码元[13]。伪随机序列也即M序列,是一种伪随机序列、伪噪声(PN)码或伪随机码。随机序列也是常被选作为训练码元。下面通过上述3种指标比较选择合适的训练码元。
由MATLAB生成长度为2000的高斯序列,进行k-means聚类数字化称为数字化序列,利用MATLAB生成长度为2000的M序列和随机序列,通过时延生成100组字典元素,通过上述的定义的码元评价参数,对以上3种码元进行量化评价得到的数值指标见表1。
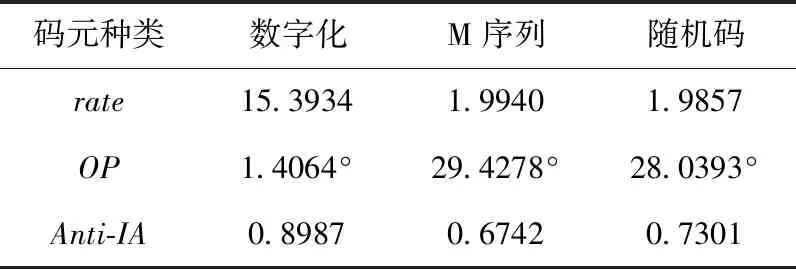
表1 比较码元的相关峰与最大干扰峰值比
根据评价指标可知,理想情况下,相关峰与最大干扰峰比为无穷大,正交偏角为0°,抗干扰能力系数为1,对以上3个性能指标计算可知,数字化高斯序列相比其它码元都有一定的优势,选取数字化高斯序列作为本文方法的训练码元。
3 全反馈信道函数估计
采用数字高斯序列与信道函数分量卷积构成的正交字典集后,由于生成高斯序列和数字化过程是对原序列近似处理,带来字典集近似正交的问题,本文提出全反馈信道函数估计算法来减小由近似正交带来的误差,并用数学归纳法证明反馈结构的功能。
3.1 匹配算法计算
基于接收端信号式(1),采用匹配算法的框架,运用以下步骤,依次求解出信道函数的参数:
(1)r[n] 与各字典元素信道参数计算

(17)
(2)设定阈值,舍弃幅值较小的多径信道参数对于接收端的信号r[n], 经过信道的衰减,依据信道参数ak的绝对值进行取舍无法判定该参数在信道函数中的影响因子,故用其相对值进行取舍。设定相对值阈值为α, 对于小于α的径舍弃,其它的保留原值,进行下一步计算。归一化公式如下
(18)
(3)在序列中找出信道参数最大径,并按式(20)更新r[n], 进行第二次信道参数分解。从分解参数中找出信道参数最大的径,并作为信道函数的参数
al=max(a0,a1…am-1)
(19)
去除已经计算出来信道函数参数对剩余参数计算的干扰
r[n]=x[n]⊗(h[m]-al·h[l])
(20)
(4)重复进行步骤(1)~步骤(3),直至分解出所有的信道参数。
3.2 全反馈结构重构信道参数
理想状态下,高斯序列是互不相关的,而且还是统计独立的,但是生成和数字化过程会对理想高斯序列近似操作,所以对于不同时延的高斯序列并非严格正交,即“完备正交字典”中的元素的相关性不为零。解决近似正交的问题,可通过改进算法结构,对于估算过程中存在其它元素的干扰,在参数估算完毕后,利用已估计参数全反馈到下一轮计算中矫正参数,称为估计参数全反馈去干扰法。其具体步骤如下,其中hmi表示第m次反馈计算后的第i个信道参数,rmi表示m次反馈计算后的接收分量:
(1)基于匹配估计信道参数hm0,hm1…hmM;
(2)接收信号r[n] 分量计算
rm1=x⊗hm1,rm2=x⊗hm2…rmM-1=x⊗hmM-1
r′m0=r[n]-rm1-rm2…rmM-1
(21)
(3)将r′m0带入式(17)重新估计h(m+1)0并更新信道参数
(22)
(4)参照(2)、(3)计算h(m+1)1,h(m+1)2…h(m+1)M-1;
(5)将m+1,重新反馈到(1)计算参数,直至计算误差符合要求。
图4为反馈迭代次数与均方误差的关系,随着迭代次数,误差将会越来越小,并采用数学归纳法证明全反馈结构可减小信道函数误差。由于字典存在正交偏角,其干扰带来的误差可以写成以下形式
ε0=
εM-1=
(23)

图4 信号参数估计的均方误差
其中,εk为rk给信道参数ai计算带来的误差,μk为第k个字典rk在ri矢量方向上的分量权重因子,本文将其称为转换因子;a′mi代表第m次迭代计算后的信道参数。
将式(23)带入式(22)中,可知在没有反馈结构时存在
(24)
其误差可表达为
(25)
加入反馈结构后,将第一次计算的参数值反馈回原结构重新计算,则带来的误差有:εk=<(a′k-ak)rk,ri>=(a′0k-ak)μk
第一次反馈计算参数则有
(26)
第一次反馈计算后的误差记为
(27)
(1)数学归纳法第一步:证明第一次迭代的误差e1小于不迭代(第0次)的误差e0
(28)
归纳法第一步可用实际数据证明,如图4可例证第一次的迭代误差小于不迭代误差。
(2)数学归纳法第二步:给出条件:第k次迭代的误差比第k-1次迭代的误差小
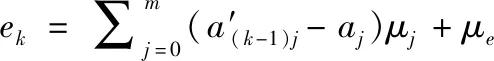
(29)
(3)数学归纳法第三步:由第二步的条件,推导第k+1次的误差小于第k次的误差成立
(30)
由ek=a′kj-aj,ek=a′(k-1)j-aj。 将等式右边带入差值计算:故ek-ek-1=(a′kj-aj)-(a′(k-1)j-aj)=a′kj-a′(k-1)j。 由数学归纳法第二步条件,可知ek-ek-1<0, 即a′kj-a′(k-1)j<0, 将此推论结果带入可知式(30)中证明ek+1-ek<0成立。
反馈计算后,误差是逐渐减小的。最先估算出来的信道参数受其它信道参数影响大,具有较大的估计误差,也会对后面信道参数产生影响。在重新估算过程中,由反馈结构将其它接收分量从接收信号r[n] 中减去,滤除其它信道参数的影响,重新估算,将干扰降到最低。
4 仿真验证与结果分析
对于水声通信中的信道函数估计算法,实时性、准确率、计算量等都是信道估计算法的重要评估参数。本文在MATLAB平台上,设置相同的模拟信道环境,分别仿真DFE算法、DFElms算法、cosamp算法、MP算法、OMP算法及其组合算法和本文提出估算方法,分别在准确率、计算复杂度等方面进行对比。
4.1 计算复杂度分析
为对比不同算法的计算复杂度和计算量,设置相同的实验环境下,现设置相关的参数变量如下,均衡算法相关参数:N训练序列长度、n迭代次数、M滤波器长度、L字典个数、2l稀疏度估计。计算量:Calculated amount(·),表示为Cal(·)。
在信道估计函数中,整体而言,匹配算法相比均衡算法的计算复杂度要低,因为均衡算法的收敛较慢。从表2、表3中计算量和计算复杂度的分析可知,匹配算法计算复杂度相比均衡类算法计算复杂度要小,计算量对应的也会小得多。传统匹配类算法Cal(基追踪)>Cal(MP)>Cal(OMP)>Cal(本文算法)。

表2 不同匹配追踪算法计算量对比

表3 不同均衡类算法每一次迭代计算量对比
本文通过算法运行时间来体现算法的计算量大小,由图5可知,本文算法相比其它几种算法具备计算量小的优势,从实验结果也可以得到,结合匹配算法的DFEcosamp的均衡算法相比其它算法也有更快的收敛速度。

图5 匹配类均衡类算法计算时间对比
4.2 信道函数准确率对比
匹配类算法采用点积计算信道函数,计算过程可屏蔽部分随机噪声;均衡类算法将接收端信号中的信号部分和噪声部分看作一个整体,即将噪声当作信道函数的一部分,估计得到的信道函数与真实的信道函数有偏差,所以均衡算法相比匹配类算法的均方误差要大;而本文采用的方法,运用高斯序列的抗干扰能力,在信道函数计算过程中采用点积运算滤除噪声,因此在3类方法中,本文算法的计算准确率将高于压缩感知的匹配算法和均衡算法。
在相同的实验环境下进行各类算法的仿真,如图6、图7 为0 dB条件下的信道函数估计结果图,在图6的局部放大图可知,本文算法与真实信道更接近,图7中均衡类算法效果都比较差,与真实信道相差较大。图8为信噪比从0 dB-30 dB的条件下,统计各方法的估计均方误差,其中DFElms与DFEnlms的性能相似,导致曲线重合。可以得到如下结论:
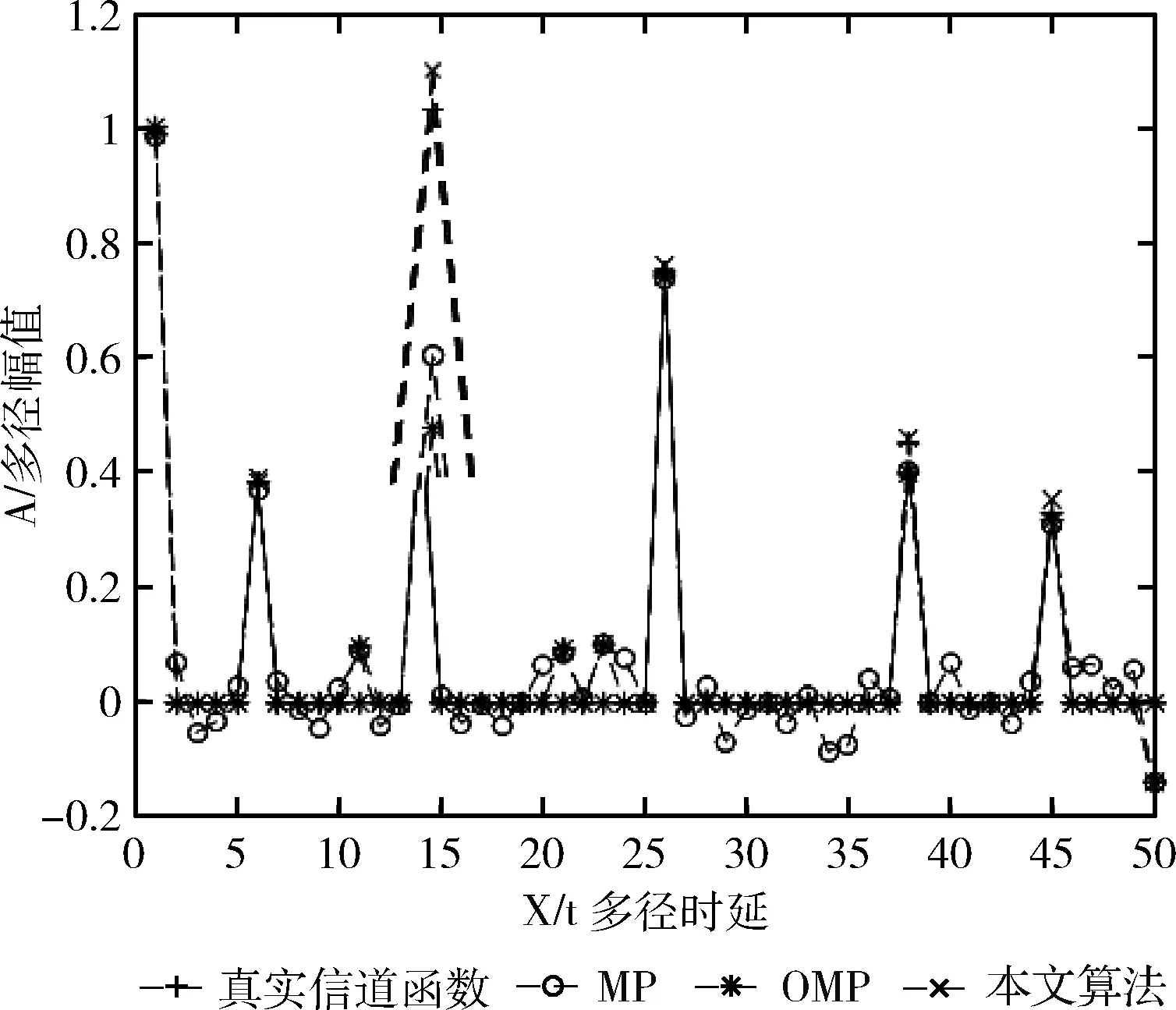
图6 0 dB下匹配类算法信道函数估计结果
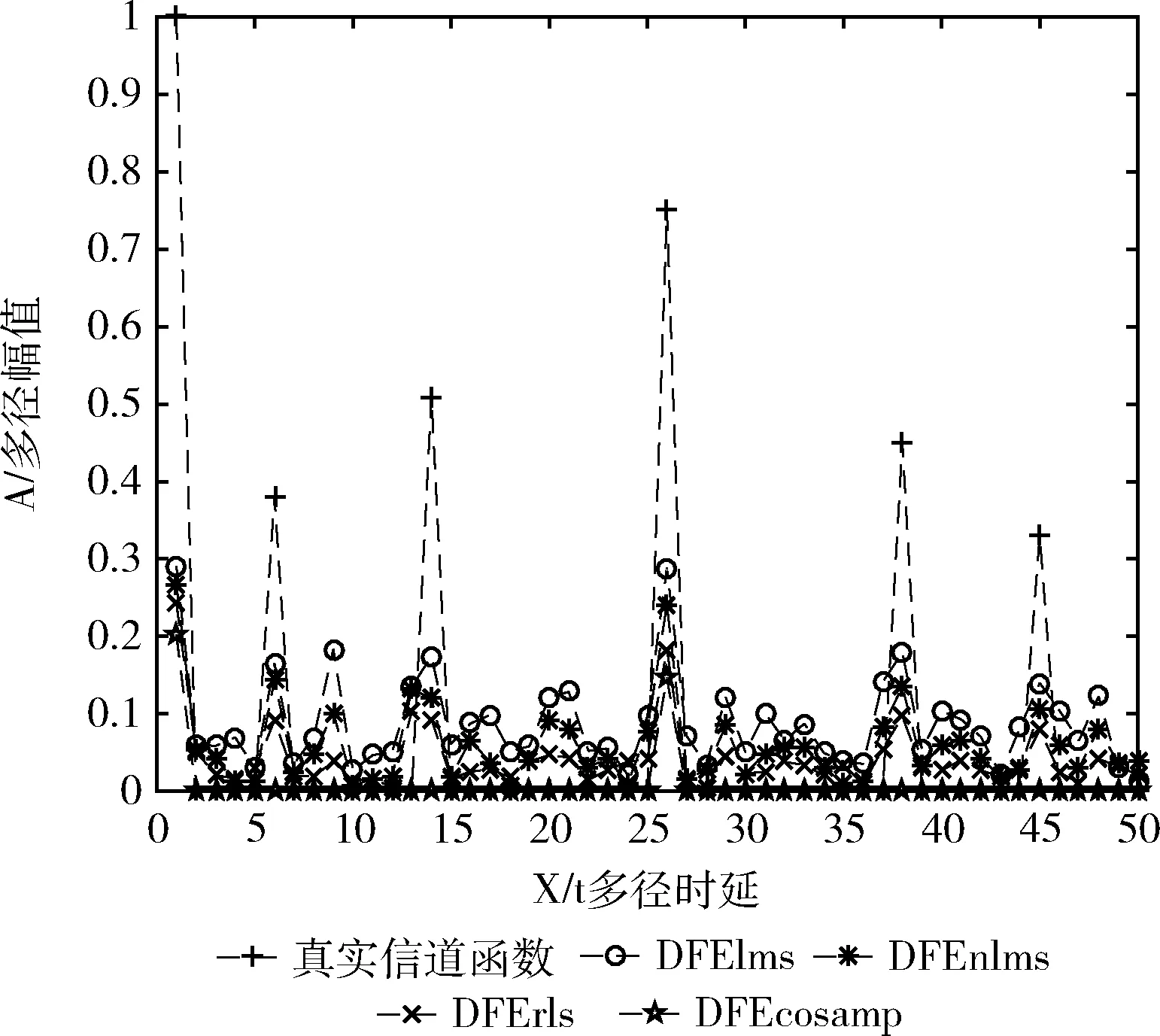
图7 0 dB下均衡类算法信道函数估计结果
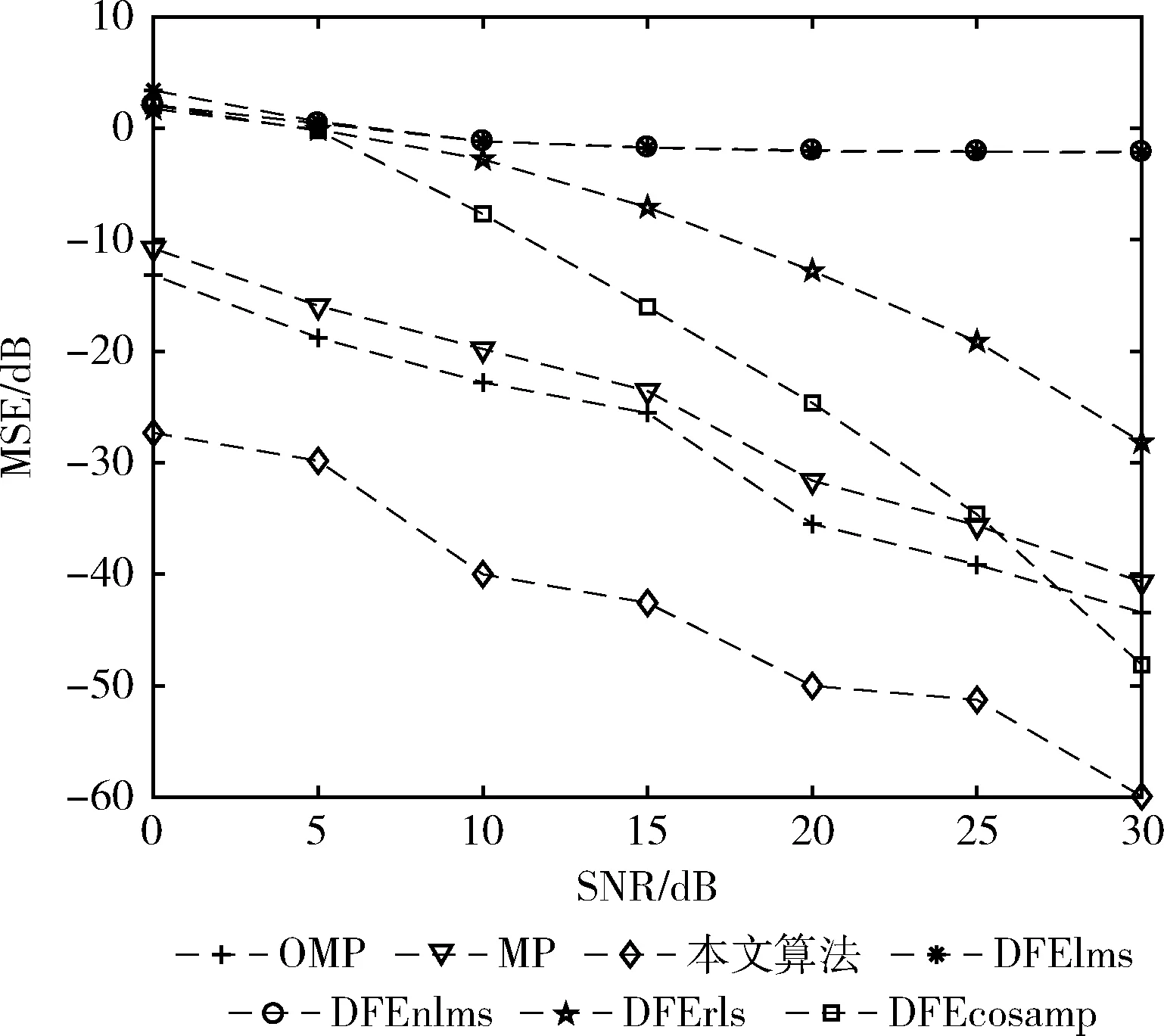
图8 匹配类均衡类算法信道均方误差对比
(1)匹配类算法虽然计算量不同,但其误差大小相近,且随信噪比减小,算法的误差增大;
(2)如理论分析结果所示,在相同信噪比的环境下,匹配类算法的MSE要小于均衡类算法;
(3)如理论分析结果,本文算法的抗噪能力优于传统均衡类算法,优于匹配类算法。
5 结束语
本文针对稀疏水声信道函数的估计问题,提出了一种基于正交字典的全反馈信道函数估计方法,给训练序列赋予正交和抗干扰的特性,在匹配算法初步估算出信道参数后,再结合全反馈结构进一步提高信道函数的准确度。仿真结果表明,本文提出的信道估计方法在噪声敏感程度上优于匹配算法,能够获取更高的准确度;在算法复杂度上优于均衡类算法和匹配均衡结合算法,以更低的计算复杂度,实现较高的准确率。
