SiCf/TC17复合材料界面剪切强度测试与有限元分析

2021-01-19范王腾飞王敏涓

材料工程 2021年1期

李虎，范王腾飞，王敏涓，黄旭，黄浩

(1 中国航空发动机集团先进钛合金重点实验室，北京 100095；2 中国航发北京航空材料研究院先进复合材料国防科技重点实验室，北京 100095)

随着航空发动机的推重比和涡轮前温度的不断提高，压气机和涡轮的级数逐渐减少，单级负荷不断增大，零件的应力水平越来越高，工况越趋恶劣，目前压气机的主要材料钛合金与镍合金的发展已经接近极限，虽有进一步的改进余地但潜力不大，不能使发动机的性能产生飞跃，因此必须寻求能够满足发动机更加苟刻要求的新材料[1]。其中连续SiC纤维增强钛基复合材料(以下简称钛基复合材料)以其优良的室温、高温强度、模量及较低的密度，优异的抗蠕变性能和疲劳性能使它具有较大的应用潜力。连续SiC纤维增强钛基复合材料是以连续SiC纤维为增强体、钛合金为基体复合而成。常用的制备工艺有箔压法、纤维-基体涂层法等。

与其他纤维增强复合材料相同，钛基复合材料的性能除了受到增强体和基体的性能影响外，还和界面的性能有很大的关系。界面强度太高，裂纹难以偏转，尖端的应力集中无法缓解，容易横向贯穿复合材料；界面强度太低，裂纹又容易沿着界面扩展，造成纤维的脱拔等问题，因此界面的相对强弱是决定钛基复合材料失效机制的关键因素，而准确评价界面的强度则是理解界面强弱的基础。

评价界面强度的主要方法有单纤维拔出法、微滴脱粘法、纤维碎裂法和纤维顶出法等[2]，评价钛基复合材料界面强度的常用方法是纤维顶出实验(push-out test)[3-7]。Majumdar等[8]通过顶出法测试体积分数为35%的SCS-6/Ti-15V-3Cr-3Sn-3Al复合材料的剪切强度为105 MPa；Eldridge等[9]测试SCS-6/Ti-6Al-4V的界面剪切强度为127 MPa；Roman等[10]测试SCS-6/Timetal-21S的界面剪切强度为80 MPa； Eldridge等[11]测试SiCf/Ti2AlNb复合材料的界面剪切强度为119.2 MPa；Osborne等[12]测试SCS-6/Timetal-21S的不同温度下的界面剪切强度，发现其由室温下的160 MPa降低至500 ℃的60 MPa左右； Haque等[5]在测试SiCf/Timatrix及含有梯度涂层的SiCf/C/(Ti,C)/Timatrix的界面剪切强度，分别为274 MPa和83 MPa，在氩气氛围经历800 ℃/100 h热处理后分别提高至313 MPa和204 MPa。

由于钛基复合材料中纤维和基体热膨胀系数差异大，高温成型冷却过程不可避免地会产生残余应力。测试钛基复合材中残余应力的方法有衍射法、腐蚀法和Raman法等。采用X射线衍射法只能测距材料表面10 μm左右的深度，测试结果的随机性较大；中子衍射法测量，虽然穿透深度增加，但同样存在测试结果的随机性较大的问题，而且测试成本较高；采用Raman光谱测试，需要剥离基体钛合金，使材料中的残余应力状态发生改变；腐蚀基体测量纤维残余应变计算残余应力的方法受纤维弯曲的影响，测试工作量大，误差也较大[13]。

制备顶出实验所需的薄片样品时又会较大程度地改变其内部应力状态，这就导致了测试用试样的应力状态和复合材料服役时不同，界面处的应力状态会影响界面强度的测试结果，因而为了评价界面的化学结合强度，本工作采用内聚力模型结合有限元的方法对复合材料高温成型冷却产生残余应力的过程、样品制备前后残余应力的变化以及纤维顶出实验进行分析和验证。

1 实验材料与方法

1.1 实验材料制备

本实验中所用的材料为连续SiC纤维增强TC17复合材料(SiCf/TC17)，纤维的体积分数为50%左右。SiCf/TC17复合材料采用纤维-基体涂层法和热等静压工艺制备，热等静压工艺参数为920 ℃/120 MPa/2 h，随炉冷却，成型后的复合材料的微观形貌如图1所示。

图1 SiCf/TC17复合材料微观形貌 (a)低倍；(b)高倍

1.2 界面剪切强度测试

界面剪切强度采用纤维顶出试验测试，将SiCf/TC17切成薄片，研磨抛光后厚度为0.34 mm，将试样置于样品台上后调整位置使得压头位于纤维上方，压头以0.1 mm/min的速率向下顶出纤维，实验的示意图见图2(a)，纤维的顶出过程可以获得位移-载荷曲线。典型的曲线见图2(b)[14]，随着下压量的增加，载荷逐渐增加，当达到Pi时，界面开始出现损伤，曲线斜率发生变化，损伤程度随着下压的继续而增大，当载荷达到最大值Pmax时，界面完全脱开，此时下压的阻力只有分离界面处的摩擦力Pfr，继续下压纤维被顶出，摩擦力逐渐降低[14]。本实验共顶出5根纤维，随后对顶出的纤维进行扫描电镜观察。

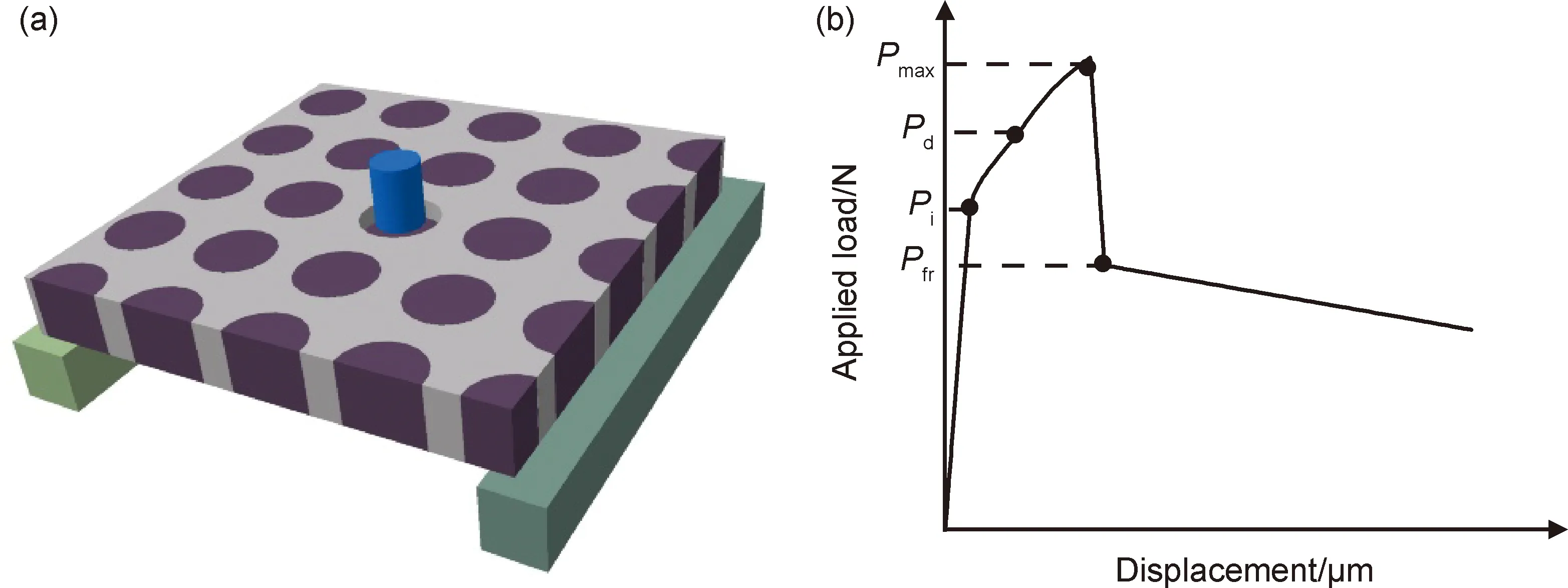
图2 纤维顶出实验示意图(a)及典型位移-载荷曲线(b)

采用哈尔滨工业大学自行研制的界面强度测试设备进行纤维顶出实验，载荷监测精度为0.1 mN，位移检测精度为0.1 μm。采用Nova NanoSEM450型扫描电镜观察微观形貌。

1.3 有限元模型建立

根据复合材料的细观结构和纤维顶出实验受力的特点，有限元模型可以视为同轴柱体的轴对称模型，模型的结构和尺寸如图3所示，SiC纤维半径R1为50 μm，其中包含厚度为2 μm的C涂层，整个模型的半径R2为71 μm，试样厚度L为340 μm，AB面为钛合金底面(顶出实验时受支撑位置)。考虑到复合材料高温成型会产生残余应力，因此整个分析过程为一个模型能自带的初始分析步和两个General Static分析步，即：(1)初始分析步(initial step)，设定初始温度场Tinitial及边界条件；(2)降温分析步(cooling step)，模拟降温至25 ℃的冷却过程，即残余应力的形成；(3)加载分析步(loading step)，压头顶出纤维过程。各个分析步的加载及边界条件如表1所示。

图3 轴对称模型

表1 边界及加载条件

SiC纤维、C涂层和Ti基体的网格类型为结构网格，单元体选择四节点缩减线性积分轴对称应力单元；界面的网格类型为扫略网格，扫略方向垂直于界面，界面单元体采用内聚力单元；压头采用解析刚体。有限元分析采用Abaqus软件。各个材料的属性见表2。

内聚力是20世纪60年代Barenblatt[15]和Dugdale[16]在经典断裂力学的基础上提出的概念，随后被Needleman等[17]完善并形成内聚力模型(cohesive zone model，CZM)。内聚力模型的基本思想是在裂纹扩展后，有两个新的应力自由表面产生，内聚力区域则是位于裂纹尖端前沿的一个扁平带区域，如图4所示[18]，内聚力区域刚受到载荷的作用时，内聚力的大小随着张开(或滑开)位移的增加而增大到应力最大值，此时内聚力区域的承载能力达到极限，开始出现损伤，由于损伤的出现内聚力区域承载能力开始下降，之后随着张开(或滑开)位移的增加反而减小，随着损伤继续扩展到临界位移，内聚力减小至零，说明此处界面已经破坏。内聚力区域的本构响应通常有双线性型、指数型、多项式型和梯形型等[18]。其中双线性型是最早被提出并与有限元广泛结合，而且能兼顾计算的精度和效率，因此本工作选用双线性型本构关系。

表2 不同温度下材料属性

图4 内聚力模型示意图

内聚力区域的初始损伤判据有4种：最大应力准则、最大应变准则、二次应力准则和二次应变准则。由于本工作关注的是纤维和基体的界面剪切强度，所以本工作中的初始损伤准则选用最大应力准则：

(1)

2 结果与分析

2.1 界面剪切强度测试结果

图5为5根SiC纤维顶出过程的位移-载荷曲线，可以看出，随着位移(下压量)的增加，载荷在逐渐增加，达到最大值时界面完全脱开，载荷突降至只有摩擦力的状态，此时纤维开始滑动，曲线呈现出较为典型的特征。从每条曲线中可以读取最大载荷与完全脱开后的初始摩擦力，得到平均的最大载荷Pmax为6.2 N，平均摩擦力Pfr为4.5 N。

图5 纤维顶出实验的位移-载荷曲线

图6为顶出纤维后样品的微观形貌，可以看出SiC纤维及其C涂层同时被顶出，纤维与基体的脱开位置位于C层和基体之间。Wu等[19]进一步对更具体的脱开位置进行了分析，发现纤维顶出时脱开位置位于C层的最外侧，因为该区域在复合材料高温成型过程中会发生界面反应与元素扩散，扩散过程会对C层的结构产生一个几十纳米尺度的影响区，该影响区为薄弱区域，因此纤维顶出时在该区域开裂。

图6 顶出实验后的样品形貌

界面完全脱开时的平均界面剪切强度τdebond和界面摩擦应力τfriction可以采用式(2)，(3)[14]计算。

(2)

(3)

式中：df为纤维直径；L为样品厚度。

经上式计算求得平均界面剪切强度τdebond为58 MPa，摩擦应力τfriction为42 MPa。平均界面剪切强度τdebond是在整个纤维长度上的平均值，因而不反映实际(局部)剪切应力，研究表明实际剪切应力在纤维长度方向上会有很大的变化[20-21]。但是摩擦应力的计算接近于真实的剪切应力，纤维移动的阻力是纯摩擦力，而界面剪切应力沿纤维长度方向上几乎是均匀的[6]。

2.2 残余应力分析

摩擦应力大小与界面处的摩擦因数μ和界面法线方向上的残余压应力有关[22]，残余压应力是复合材料高温成型(常用的温度范围为800～1000 ℃)冷却过程中由于纤维和基体的热膨胀(收缩)的差异导致的，其大小与纤维和基体的膨胀系数的差值及冷却过程的温差有关，但不能以成型温度作为其开始产生残余应力的起始温度，因为当温度较高时若存在热应力，基体在热应力的作用下会发生高温蠕变，产生一定的塑性变形使残余应力得到释放，因此只有当温度低于某一值Tinitial时才开始产生残余应力[13,22]。Tinitial的值与基体类型、体积分数等因素相关，李健康等[13]利用残余应变不平衡法研究SiCf/Ti-6Al-4V的残余应力，认为开始产生残余应力的温度是704 ℃。本工作以纤维顶出实验的位移-载荷曲线中纤维脱开后的初始摩擦力为出发点，结合有限元的方法验证Tinitial分别为700，725，750，775，800 ℃和825 ℃时初始摩擦力的计算结果与测试结果的一致性。首先需要确定摩擦因数μ的数值，原梅妮等[23]认为界面的摩擦因数为0.4时与试验结果吻合， Zeng等[24]在分析中选用的摩擦因数为0.3，何周理等[25]在0.3～0.4之间进行了验证反演，发现界面摩擦因数为0.34时摩擦力的实验值与计算值比较接近。本工作选择的界面摩擦因数为0.34。

图7为几种Tinitial温度下冷却后纤维完全脱开至顶出一定距离的摩擦力的计算结果，可以看出随着Tinitial的增加，摩擦力逐渐增大，当Tinitial为775 ℃时，软件计算结果与实验结果较为接近。因此，在后续分析中选取775 ℃作为开始产生残余应力的温度。

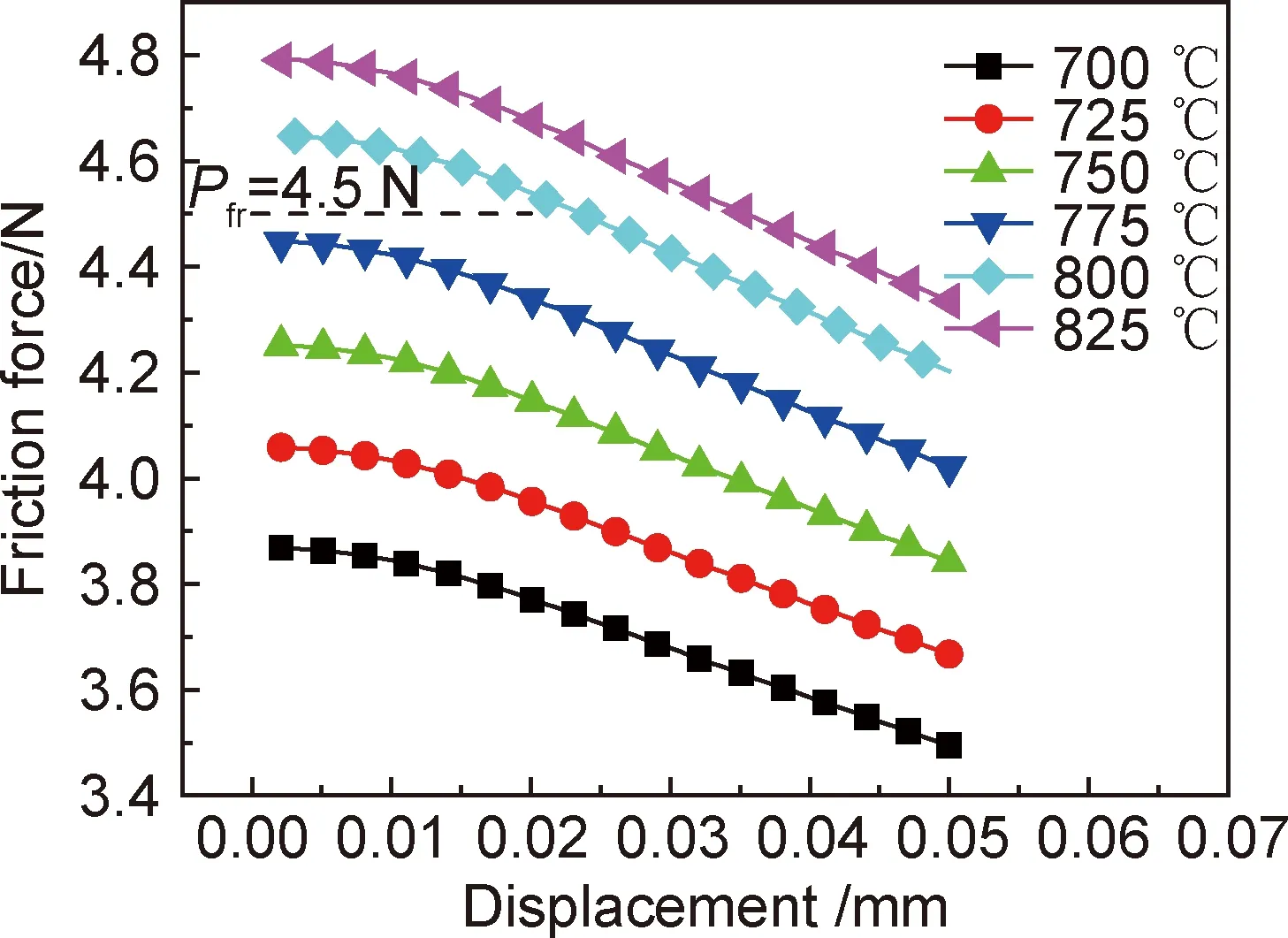
图7 摩擦力与温度的关系

纤维顶出实验所用的薄片样品是从(较大尺寸的)复合材料中切割、研磨而成，在这一制备样品的过程中，残余应力会发生较大变化，原有结构的平衡状态被破坏，形成了新的应力平衡状态。图8为样品制备前后的示意图，图8(a)为未切割时复合材料的等厚度区域，由于该区域受到周围复合材料内力的束缚，使得在成型后的冷却过程中纤维的中心A-A1、界面处B-B1及基体的边缘C-C13个位置的厚度沿着纤维方向具有相等的收缩量，即ABC面沿着厚度方向的位移相等，纤维和基体的收缩量一致，因此，界面处不存在剪切应力；而当切割成薄片以后，如图8(b)所示，内力的束缚消失，A-A1,B-B1,C-C13个厚度的收缩量不再一致，基体的外侧C-C1收缩量最大，收缩量的不一致会导致界面处产生残余剪切应力，残余剪切应力的大小及分布与样品的厚度和复合材料的体积分数有关，该残余剪切应力的存在使得界面在纤维顶出实验中未加载时已经承受了一定的剪切应力。

图8 样品制备前(a)后(b)边界条件示意图

图9为体积分数为50%的复合材料从775 ℃冷却至25 ℃后的中等高处(图8(a)中虚线位置)沿着径向上的应力分布情况，可以看出SiC纤维及C涂层各个方向均处于压应力的状态，应力分布均匀，钛合金沿着半径方向受到压应力，沿圆周方向和纤维方向为张应力。界面处不存在剪切应力。

图9 样品制备前残余应力分布

切割成薄片后复合材料内的残余应力变化较大且分布不均匀，除了界面处的残余剪切应力之外，其余应力不做讨论。文献[6]中推荐纤维顶出实验的样品厚度为0.25～0.50 mm之间，复合材料常用的体积分数有35%，42%和50%等，因此除了实验样品规格的薄片试样之外，本工作还对厚度为0.3，0.4 mm和0.5 mm 的3种体积分数的薄片试样进行了界面残余剪切应力的计算分析。

3种体积分数的复合材料切成不同厚度的薄片后界面处的残余剪切应力沿着厚度方向上的分布如图10所示，可以看出在接近表面的区域残余剪切应力较大，随着向中心的移动，剪切应力逐渐减小至零，应力的分布以样品厚度的中点为中心呈现大小相同方向相反的对称分布；纤维的体积分数越低，近表面处的最大剪切应力越大，体积分数为35%时最大应力值约为275 MPa，体积分数为50%时最大应力值约为230 MPa；随着样品变厚，远离表面处的界面残余剪切应力会降低。纤维顶出实验所用0.34 mm的试样的界面残余剪切应力最大约为230 MPa。

图10 薄片试样界面处的残余剪切应力分布

2.3 界面化学结合强度

纤维顶出过程中，界面的分离并非瞬间完成，而是一个出现裂纹和裂纹扩展的过程，这一过程可视为一个准静态的微区失效过程，文献[23]在考虑到残余剪切应力的基础上从宏观角度提出了平衡公式：

P=Fr+Ff+Fe

(4)

式中：P是顶出纤维时施加的载荷；Fr是界面残余剪切应力引起的剪切力；Ff是摩擦力；Fe是界面的化学结合力。Fe与未脱开尺寸和界面化学结合强度τc有关。界面的化学结合强度τc是复合材料的固有属性，是破坏界面化学结合键所需的应力水平。而且复合材料服役时界面处的应力状态与纤维顶出实验时状态不同，因此确定其化学结合强度τc对复合材料的工程应用及相关的工艺调整才具有实际意义。

界面的化学结合强度τc难以用实验的方法测得，且剪切残余应力的分布会随着界面裂纹的扩展而再分配[24]。这些不足可以通过有限元的方法来弥补，因此本工作采用内聚力模型结合有限元的方法来分析验证界面化学结合强度τc。采用内聚力模型时，界面的断裂韧度GⅠC对计算结果影响较大[26]，文献[7]中认为在400 ℃以下钛基复合材料界面的韧性为10 J/m2左右，本工作的界面断裂韧度GⅠC为10 J/m2。内聚力的初始损伤判据即为界面的化学结合强度τc，从图10中可以得知未施加载荷时界面处已经存在230 MPa的剪切应力，因此选择300，350，400，450，500 MPa和550 MPa作为界面化学结合强度分别进行分析验证。

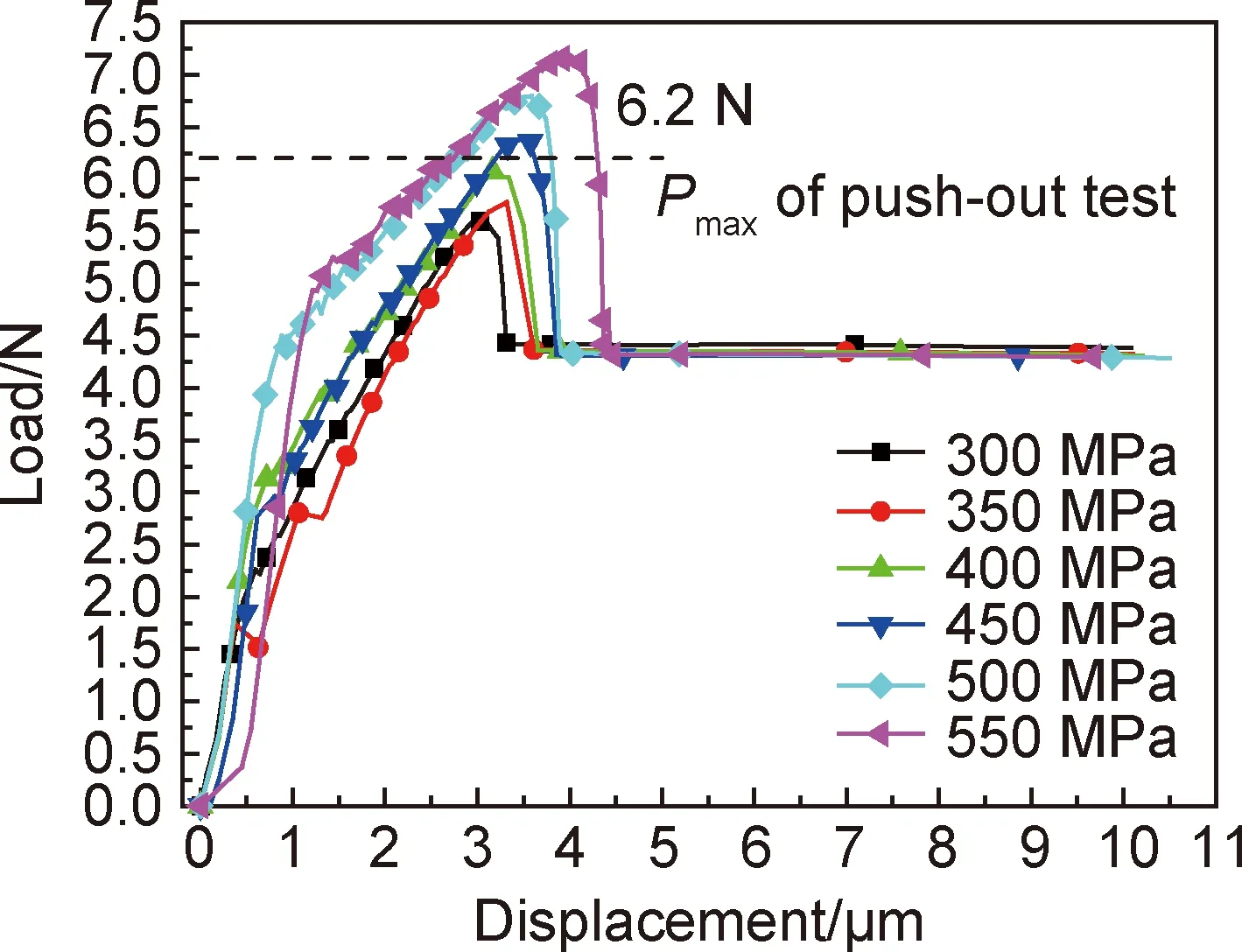
图11 不同界面化学结合强度的位移-载荷曲线

图11为室温下几种不同界面化学结合强度下纤维顶出实验的计算曲线，从图中可以看出，曲线的峰值载荷随着界面化学结合强度的增加而增加，当界面的化学结合强度为450 MPa时，计算结果与实验结果相接近。原梅妮等[23]和Zeng等[24]采用弹簧模型研究SCS-6/Timetal 834的界面化学结合强度分别为550 MPa和500 MPa；何周理等[25]采用内聚力模型研究SCS-6/Timetal 834的结果为500 MPa；Chandra等[22]认为SiCf/Ti-6Al-4V和SiCf/Ti-15V-3Cr-3Sn-3Al的界面化学结合强度分别为600 MPa和350 MPa时，测试结果和计算结果较为吻合。可以看出通过纤维顶出实验求得的平均界面剪切强度为58 MPa，而界面处的化学结合强度为450 MPa左右，两者的差异正是薄片试样界面处的残余剪切应力造成的。

本课题组认为，界面强度应结合复合材料微区损伤处裂纹的形状、应力状态等因素来分析裂纹扩展情况，即从断裂力学的角度来研究复合材料的损伤问题。裂纹沿着较脆的界面时，往往为Ⅱ型裂纹，此处采用线弹性断裂力学较为合适；裂纹在韧性材料Ti基体中时，往往为Ⅰ型裂纹，此处采用弹塑性力学较为合适，两者同时出现在复合材料中时问题会更为复杂，加之界面两侧材料模量不同，基体中微裂纹形状复杂、尺寸不确定等因素使得研究难度加大。但针对钛基复合材料制备工艺优化的方向较为明确，即通过调整界面和基体的性能，使得复合材料出现损伤后，可以通过界面局部开裂、基体裂纹尖端钝化等方式使得应力集中程度下降，阻止微裂纹的扩展，让复合材料得以继续使用。