强扰动环境下水下滑翔机编队稳定性分析

张润锋，杨绍琼,3，牛文栋,3，杨秀竹，高维强

(1. 天津大学 机械工程学院机构理论与装备设计教育部重点实验室，天津 300350；2. 天津大学 青岛海洋技术研究院，山东 青岛 266237；3. 青岛海洋科学与技术试点国家实验室海洋观测与探测联合实验室， 山东 青岛 266237)

0 引 言

水下滑翔机作为一种依靠浮力驱动的新型海洋机器人，逐渐在海洋现象观测与水下目标探测应用中崭露头角[1]。随着海洋观测技术的逐渐成熟，单一的水下滑翔机观测已无法满足广域观测、同时探测的需求，因此水下滑翔机编队应用成为目前发展的趋势。美海军研究院在20 世纪90 年代构建了以水下滑翔机为核心平台的自主海洋监测网（AOSN），观测近海和沿海区域内的各种重要海洋特性，并于2000 年、2003 年和2006 年在美国蒙特利海湾进行了一系列海洋观测实验[2]；美国海洋大气署组建了综合海洋观测系统（IOOS），并于2012 年8 月成立水下滑翔机数据中心。IOOS 观测系统已经建立了持续的气候生态观测区、危机快速响应区与飓风密集区3 个常规性观测网[3]；由英国、法国等国科学家在2005 年组成的欧洲滑翔机观测站（EGO），主要目的是研究如何协调组织水下滑翔机编队，实现全球性、区域性及近海岸等不同范围内的长期海洋观测任务[4]；美国海军在2006 年建立近海水下持续监视网络（PLUSNet），用于密切监视并预测海洋环境，通过网络化协同工作，对安静型常规潜艇进行探测、分类、定位和跟踪[5]；澳大利亚在2007 年建立的综合海洋观测系统（ANFOG）负责水下滑翔机编队的运行维护，并用来对澳大利亚周边海洋和大陆架海域的物理、生化现象的观测和预报[6]；2018 年4 月，美海军海洋局已实现协控50 台水下滑翔机的目标，并寻求高效和自动化的方法控制100 台滑翔机；2020 年3 月，美国海军科学家着手优化水下滑翔机的观测位置以提高数据协同化能力，实现精确的模式预报。国内对于水下滑翔机编队的研究较晚，2014 年天津大学在西沙海域采用3 台水下滑翔机进行编队试验，验证水下滑翔机编队的协同控制能力[7]；2017 年中科院沈自所采用12 台水下滑翔机在南海北部进行中尺度涡观测，实现了涡结构的反演[8]；同年，青岛海洋科学与技术试点国家实验室联合天津大学等单位，以水下滑翔机为主，在南海进行海洋多参数的观测，实现了对海洋流场及中尺度涡现象的反演[9-10]；2019 年5 月由青岛海洋科学与技术试点国家实验室启动了含水下滑翔机等共计74 台无人设备的海洋组网观测计划，初步验证了异构无人编队的运动规律和控制机理，并对中尺度结构进行了重构，是迄今我国最大规模的异构综合观测系统。在水下滑翔机编队观测或探测过程中，水下滑翔机的稳定性运动是进行协同控制的关键要点。在水下滑翔机稳定性分析方面，牛文栋、赵宝强等[11-12]分别采用李雅普诺夫方法分析了水下滑翔机的单机稳定性，为水下滑翔机的设计和控制提供理论依据；薛冬阳等[7]针对不确定海洋环境下的水下滑翔机编队运动控制，采用李雅普诺夫分析了多机编队运动过程中的稳定性，为队形变换及控制提供了理论依据。然而，目前针对不同水下滑翔机编队队形的稳定性分析趋于理想化，因此，本文针对强扰动环境下的不同水下滑翔机编队构型进行稳定性分析，并进行实验仿真，验证不同构型下的稳定性，为未来海试应用奠定理论基础。

1 水下滑翔机编队网络化及稳定性评价体系

1.1 水下滑翔机编队系统抽象

复杂网络作为目前物理界的一个新兴的研究热点，近年来在科学研究中具有广泛应用[13]。水下滑翔机编队作为复杂的多智能体系统，可以采用复杂网络方法进行抽象化处理。为了便于编队稳定性分析，构建特定的编队队形。首先，将节点定义为每台水下滑翔机，各水下滑翔机之间的连接作为连边，将水下滑翔机编队系统视为一个网络，利用复杂网络理论分析水下滑翔机编队系统的稳定性变化。水下滑翔机编队网络构型和示意如图1 所示。图1（c）是复杂网络的层次结构，包括结构层、通信层和任务层。

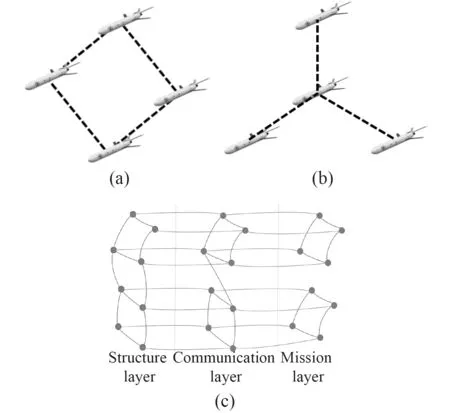
图 1 水下滑翔机编队构型及网络示意图Fig. 1The formation configuration and schematic of underwater glider fleet

1.2 水下滑翔机编队稳定性评价体系

为建立水下滑翔机编队的稳定性评价体系，考虑衡量稳定性的指标，并综合分析每个指标的权重，最终采用归一化方法推导出稳定性综合评价体系。

1.2.1 评价指标

节点是复杂网络的重要组成部分，节点数量直接影响复杂网络的结构构造和性质。表征节点重要性的指标之一是节点集中因子，如节点度。除此之外，还可通过计算网络中传输的信息量来检验其重要性，如网络效率等。为了综合评价水下滑翔机编队稳定性，本文以节点数、平均节点度、聚类系数和网络效率作为指标[13]，各指标定义如下：

1）平均节点度。在网络中与该节点直接相连的边长数量，如下式：

其中N 为节点个数，ki为第i 个节点的节点度为平均节点度。

节点度在本文的研究中主要分为2 部分，分别如下：

进一步地，平均节点度可表达如下：

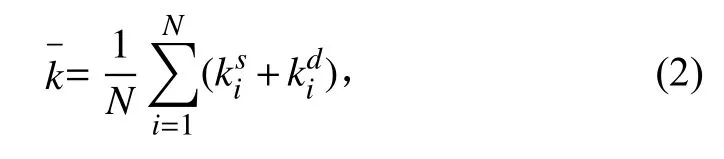
2）集群系数。单个节点 vi的集群系数Ci是连边数量 Ei占据该节点与相邻节点之间可能的所有连边总数量的比例。编队网络的集群系数C 是所有单个节点集群系数Ci的平均值。

3）网络效率。定义两节点 vi与 vj之间距离为 dij，其倒数即为两节点之间的效率 εij，编队网络的效率 ε定义为每个节点的效率的平均值，如下式：

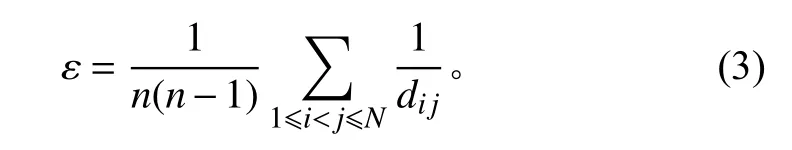
1.2.2 指标权重分配

针对不同的水下滑翔机编队队形而言，不同的指标权重比值会产生不同的评价结果。为了精确地描述稳定性的变化，合理分配各指标的权重具有重要意义。在指标权重分配方面，可分为主观权重分配方法和客观权重分配方法。主观方法包括Delphi 法，AHP法等；客观方法包括相关系数法，因子分析法等。本节选用灵敏度分析方法进行权重分配。

每个指标的权重表达式如下式：

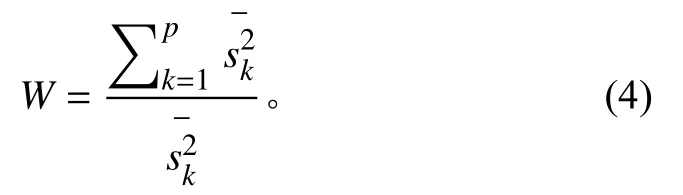
1.2.3 综合评价体系

采用归一化方法，最终水下滑翔机编队稳定性的综合评价体系如下式：

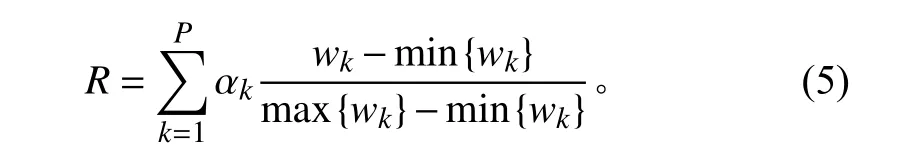
其中R ∈[0,1]，其值越高，表征编队系统的稳定性越好。

2 基于Leader-Follower 方法的水下滑翔机编队模型

为准确地进行编队系统的仿真分析，基于Leader-Follower 方法建立无扰动条件下的水下滑翔机编队的运动学模型，之后为量化扰动的强度影响，进一步在模型中补充流场因素进行分析。

2.1 无扰动下水下滑翔机编队运动学模型

笛卡尔坐标系下2 台水下滑翔机的Leader-Follower结构如图2 所示。图中各符号描述定义如表1 所示。

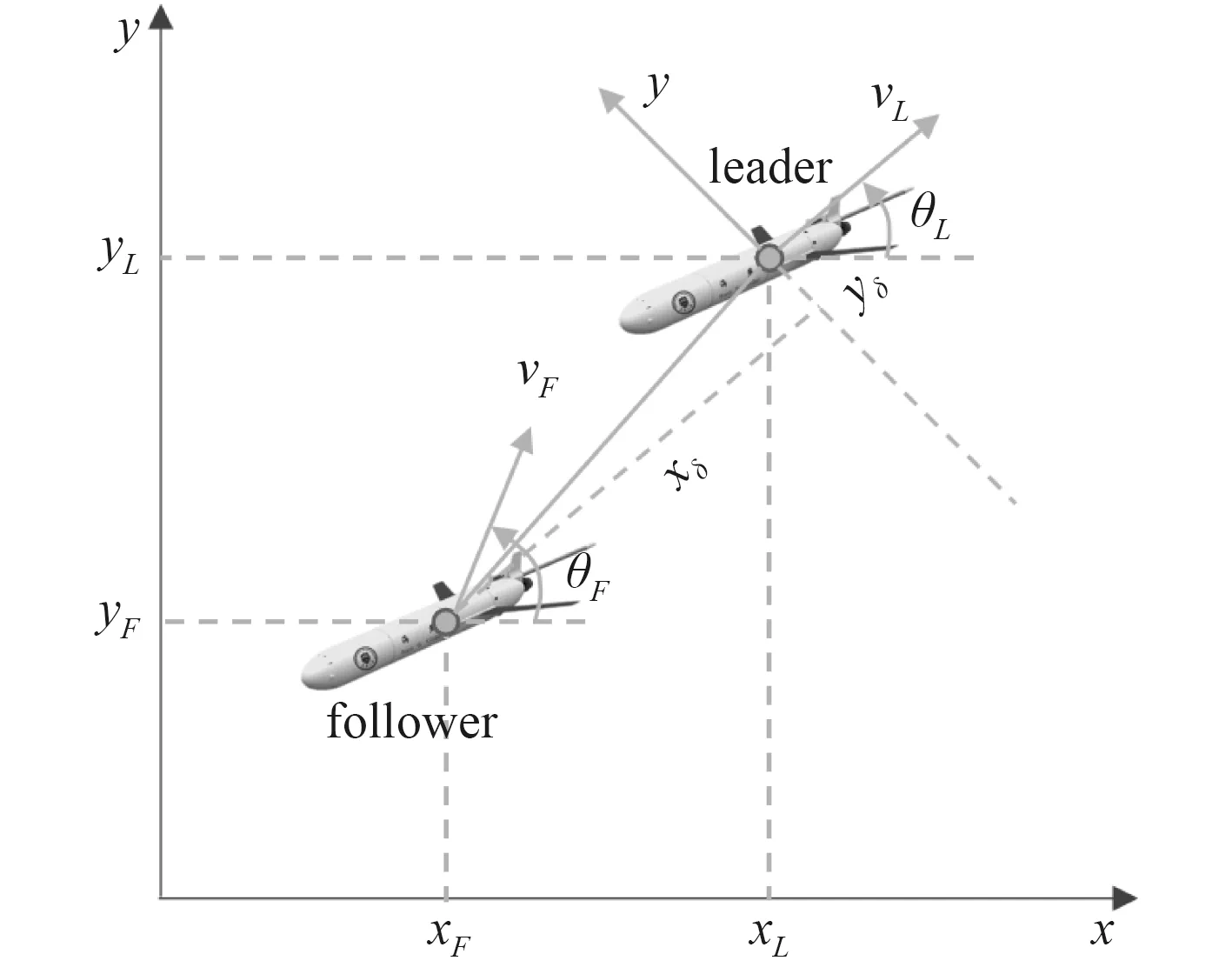
图 2 Leader-Follower 结构示意图Fig. 2Schematic of leader-follower structure

表 1 x 符号描述Tab. 1 Symbol Description

根据图2 示意以及三角函数关系，可得：

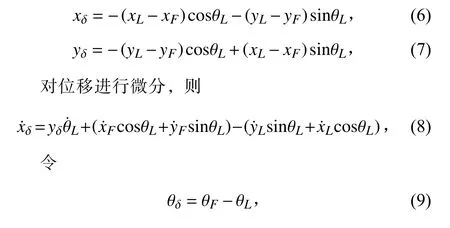
代入式（8）得：

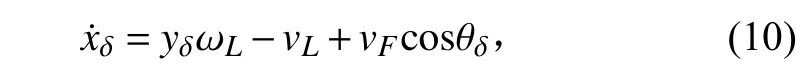
其中 ωL是领航者的角速度。

同理，对于 yδ，可得：

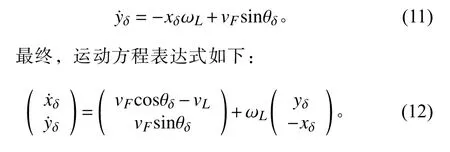
2.2 有扰动下水下滑翔机编队运动学模型

结合实际海洋情况，在水下滑翔机运动过程中，外界流场是主要的扰动来源。以流场为例进行分析，流场扰动可分解为沿x 和y 轴2 个方向的扰动分量，其影响分别定义为 ωx和 ωy。基于前述假定，其表达式如下式：

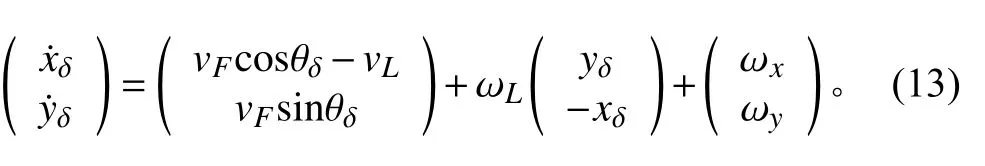
3 案例仿真分析

在进行实例仿真时，采用30 台水下滑翔机配置为不同的领航-跟随者模型进行稳定性分析（见图3），具体参数描述如表2 所示。

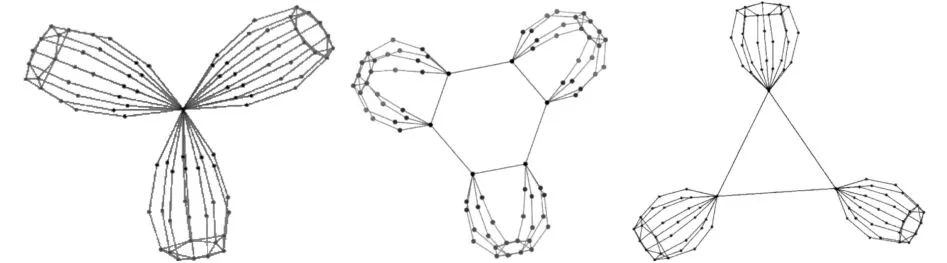
图 3 水下滑翔机编队网络结构图Fig. 3The network structure of underwater glider fleet

表 2 实例参数描述Tab. 2 Parameters description of case

在进行稳定性仿真分析时，强扰动定义为强海流，分别为ω=1, 1.5, 2.0, 2.5 m/s。

为了将仿真过程可视化处理，领航者和跟随者之间的距离变化如图4 所示。图中x 轴代表时间，y 轴代表运行过程中距离与初始距离的比值关系。3 种构型的稳定性分析结果如图5 所示。

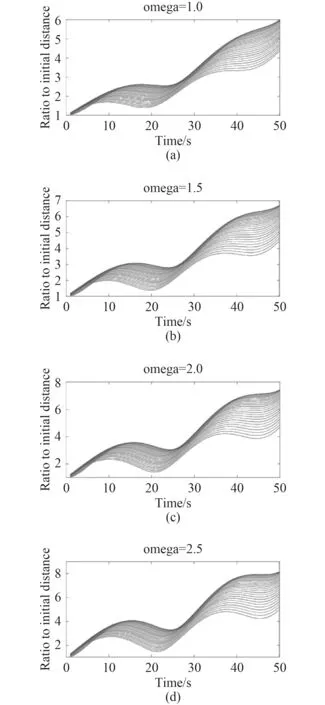
图 4 不同扰动条件下的稳定性变化（每一条线表示一个跟随者）Fig. 4Stability variation under different disturbances（each line in the figure indicates a follower）

从图5 可以看出，对于固定构型的水下滑翔机编队来说，外界扰动对整体的影响趋势一致，均在28 s左右重归稳定状态。但是当外界扰动过大时，会较快达到不稳定状态，这与实际情况相吻合。采取稳定性指标R 分别对3 种编队构型在不同扰动下的稳定性进行评价，第1 种构型稳定性较差，第2 种构型稳定性较好，第3 种构型稳定性最好。当编队中各水下滑翔机的区域分布较广时，即领航者数目较多时，编队构型的稳定性较好。

4 结 语

本文提出一种基于复杂网络理论的水下滑翔机编队稳定性分析方法。首先根据水下滑翔机编队运动特性提出一种稳定性综合评价方法，通过建立编队与复杂网络系统之间的参数映射关系，对不同水下滑翔机编队队形的稳定性进行仿真。通过试验仿真分析，验证了不同水下滑翔机编队构型在不同强度的外界扰动情况下的稳定性变化情况，结果为后期编队任务规划和组网控制奠定了理论基础。

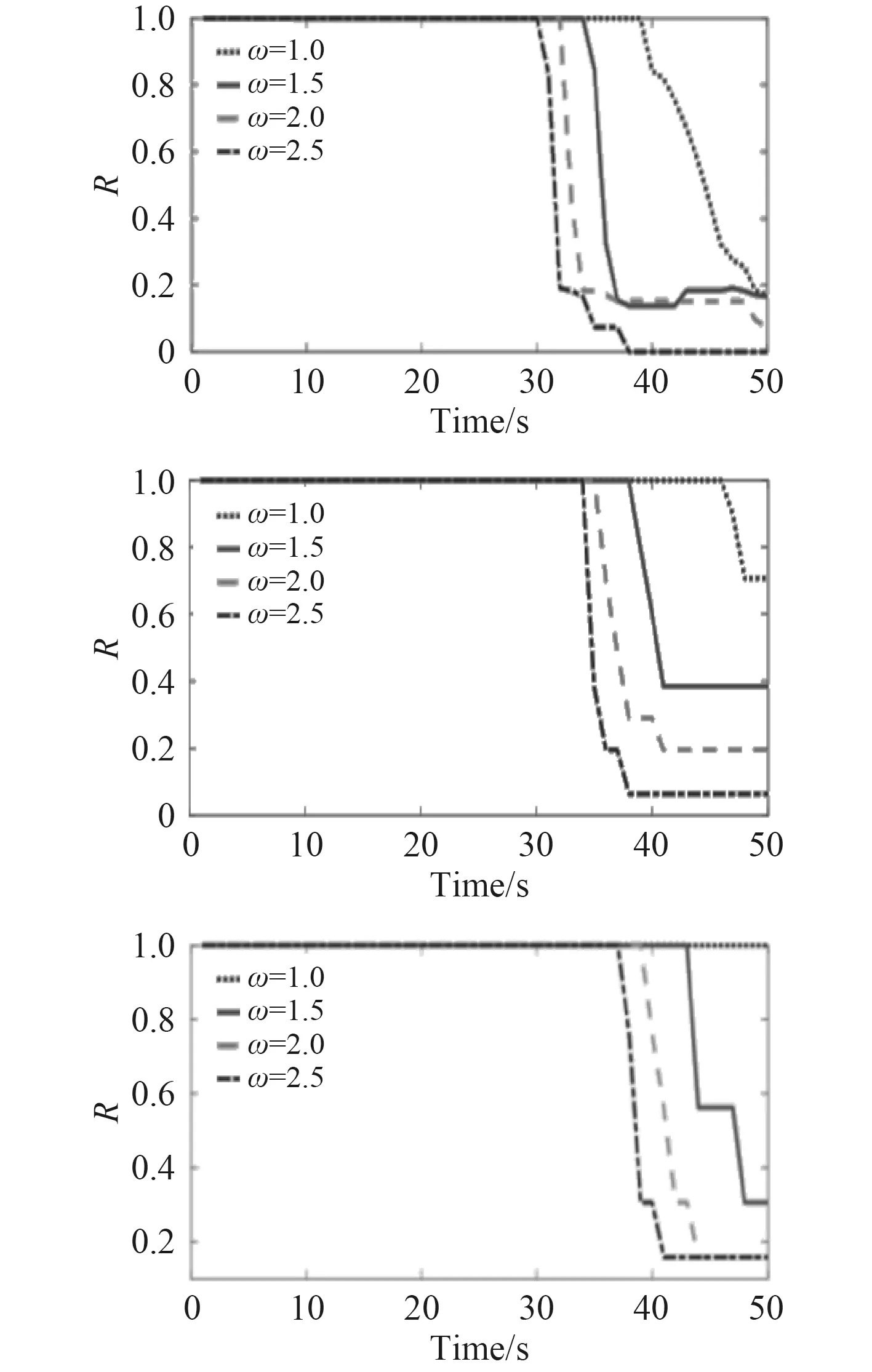
图 5 三种结构的综合稳定性指标Fig. 5The synthetic stability index of three structures