基于混合时间窗下动态需求的补给船航线规划

王 杰，费 鹏，陈 凯

(大连海事大学 交通运输工程学院，辽宁 大连 116026)

0 引 言

目前，中国已成为世界主要的远洋渔业大国之一。远洋渔船作业时，经常会遇到生产生活物资供给不足、捕捞渔品无处存放等问题，影响到远洋捕捞的效率。通过补给船的专业运输，为海上作业渔船提供渔具、食物与燃油等生产生活物资，并将渔船的渔获运回陆岸基地，可以有效解决上述问题。

针对补给船航线规划问题，诸多学者进行了研究并将其视为车辆调度问题[1-2],曹守启等[3]对静态条件下远洋渔船补给航路问题进行了研究，采用回归分析法预测其完成生产工作的初始等待时间，建立关于航路和补给时间的多目标优化模型，使其能够实现补给船最大运输效率。关于路径优化问题，彭鑫等[4]针对传统的配送车辆路径问题，增加客户的混合时间窗和车辆在客户点的服务时间，基于此构建车辆路径问题的数学模型；张文博等[5]通过针对动态需求下带时间窗的车辆路径问题，以最小配送成本为目标，使用两阶段规划策略进行求解；B.J. POWEL等[6]综合考虑船队在航行过程中所遇到的多种影响因素，结合线性规划和整数规划建立混合优化模型；陈龙等[7]采用动态规划法，构建在多个阶段进行投资决策的远洋渔船编队优化网络模型。综上，国内外关于路径优化问题研究较多，但针对补给船航线规划的研究却寥寥无几，且没有综合考虑远洋渔船的时间约束以及动态需求[8]。为此，针对补给船的航线规划问题进行探讨，具有较大的研究空间和现实意义。

主要研究补给船的最优补给航线问题，以补给成本最小为目标函数，构建基于混合时间窗下需求动态变化的补给船航线规划模型，提高补给效率及优化服务。

1 问题描述及模型建立

1.1 问题阐述

海上环境复杂多变，远洋渔船作业及其补给特点鲜明。一是远洋渔船通常组成捕捞船队，聚集在渔场附近活动，空间位移相对较小；二是从长期来看，远洋渔场资源丰富，所捕渔获量具有连续性，利于预测；三是为增加捕捞时间，远洋渔船通常会把之前所打捞的渔获由补给船捎回，末期部分渔获会由渔船返程时自行带回。

基于此，补给船根据任务目标依次给待补给渔船运送生产生活物资，并将渔获带回。管理人员在安排补给航线时，需要考虑以下因素：一是补给船到达时间是否会影响到渔船正常作业，若在渔船生产生活物资耗尽后到达，渔船人员的生产生活将陷入困境；若在渔获满载后到达，将增加渔船非作业等待时间；二是在补给船进行补给时，渔船会持续进行海上作业，船上的生产生活物资以及渔获量也会产生相应变化。因此，补给船管理者要合理安排补给方案，提高补给船的作业效率。

1.2 模型假设

由于受到海洋复杂环境的影响，补给船的补给作业也会受到各种因素的干扰，因此笔者做出以下假设：

1)补给船对于补给方案的处理以及补给船调度所需时间忽略不计。

2)数条补给船在接到任务时，开始从同一地点出发，并以经济航速行进，且最大载货量、最远航行距离基本保持一致，不受周围环境等因素影响。

3)补给船开始补给作业时，渔船与补给船之间的相对距离不变。

4)渔船的生产生活物资消耗量和捕捞量具有一定的连续性。

5)补给船完成补给任务后返回出发地。

1.3 补给船航线规划模型建立

综合考虑补给船受到补给时间的限制以及渔船作业的特点，提出构建混合时间窗下需求动态变化的补给船航线规划模型。

1.3.1 惩罚函数

补给船的主要任务是保证远洋捕捞人员的正常生活要求，减少渔船非作业等待时间，为此在构建目标函数时，建立惩罚成本函数。将渔船的剩余生产生活物资使用时间用T1表示，渔船的渔获满舱时间用T2表示。

1)当T1≤T2时

在此情况下，补给船的时间限制为硬时间窗，其惩罚函数如图1，具体惩罚函数为：

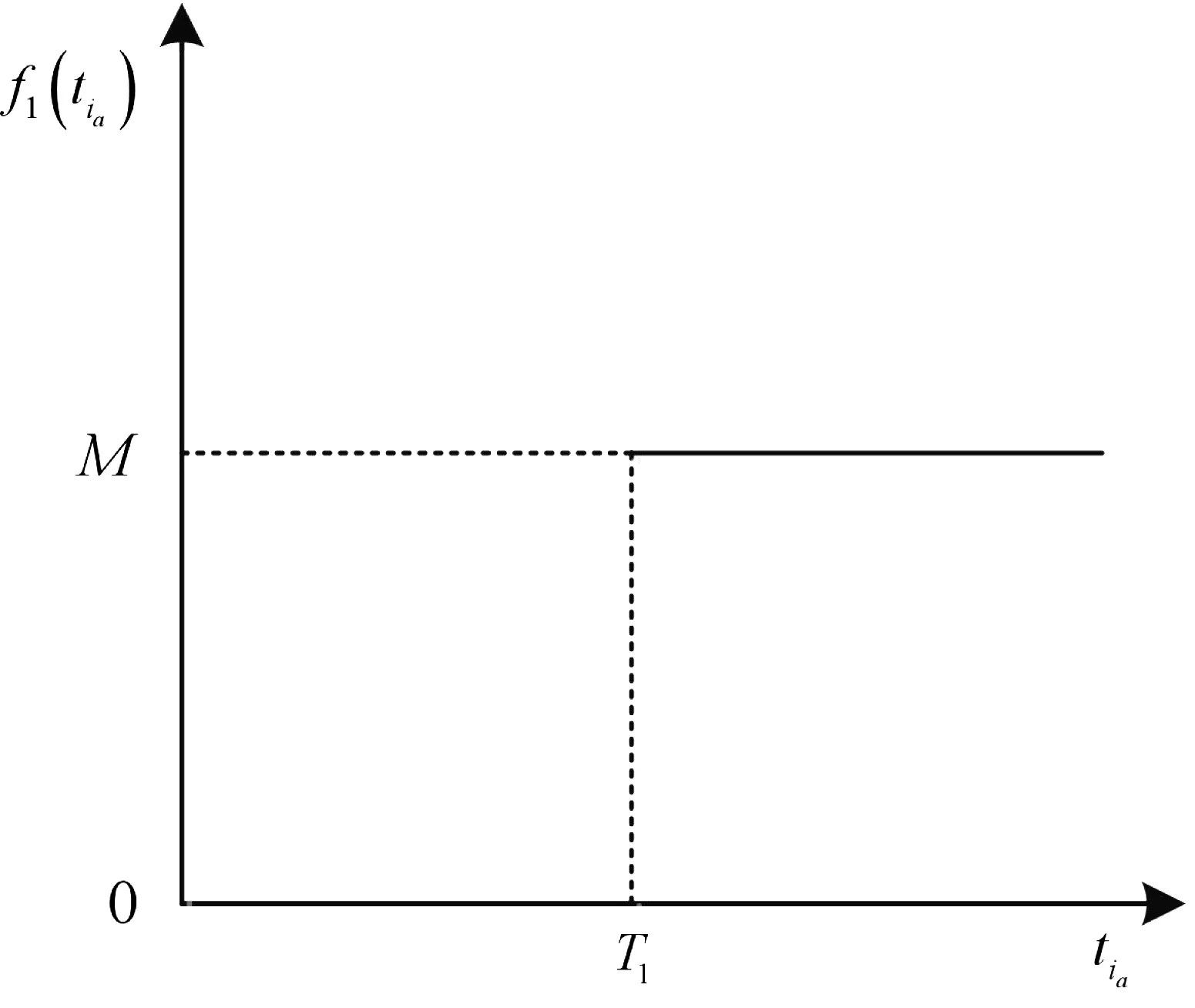
图1 T1≤T2Fig. 1 T1≤T2

(1)

其中M为比较大的正数。经整理得：

f1(tia)=Mmax(tia-T1,0)

(2)

2)当T1>T2时

当补给船的到达时间在T2、T1之间时会产生惩罚成本，且偏离T2越大，其惩罚成本越高，但到达时间不能大于T1。在此时间段内，假设惩罚成本为线性增长，其惩罚函数如图2，具体惩罚函数为：

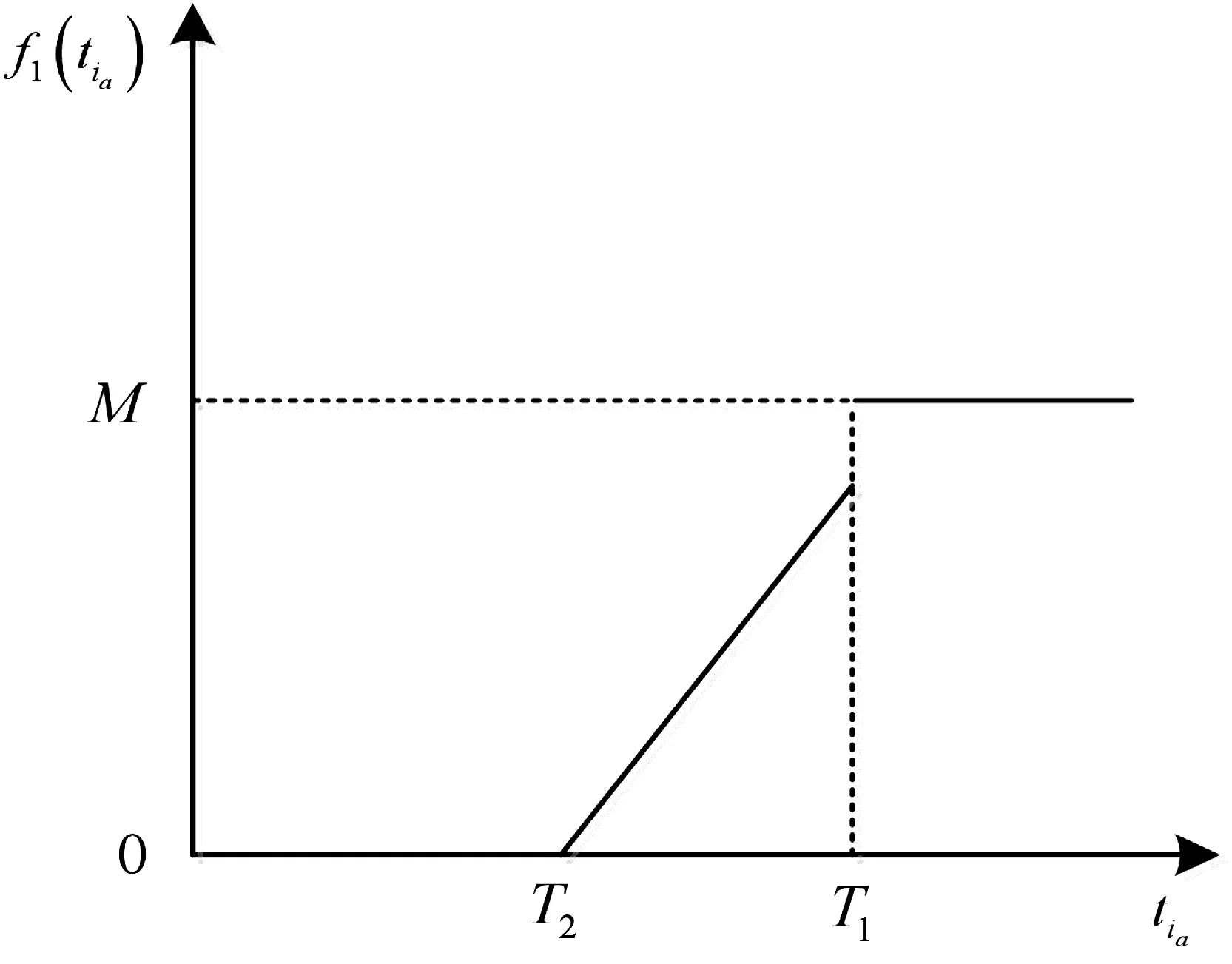
图2 T1>T2Fig. 2 T1>T2

(3)

其中M为足够大的正数。经整理得：

tia>0

(4)

综合1)、2)两种情况，统一得出其惩罚函数为：

(5)

式中：tia为补给船a到达渔船i位置所用的时间；P为补给船受到的单位时间惩罚值。

1.3.2 渔船的物资需求量和渔获变化量

补给船的到达时间直接影响着渔船的实际生产生活物资需求量和渔获卸载量，而到达时间由补给船的海上航行时间和对之前渔船的服务时间决定。因此当补给船a到达渔船i时，其生产生活物资实际需求量应为初始需求量与增加量之和；渔获的实际卸载量应为初始渔获量与增加量之和。渔船的实际生产生活物资需求量以及渔获卸货量计算公式为：

(6)

(7)

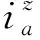
式(6)为渔船的实际生产生活物资需求量；式(7)为渔船的实际渔获卸载量。

1.3.3 优化模型建立

根据以上分析，笔者以最小补给成本作为目标函数，渔船生产生活物资需求量和渔获卸载量函数为主要约束条件之一，构建以下优化模型：

(8)

s.t.

(9)

(10)

(11)

(12)

(13)

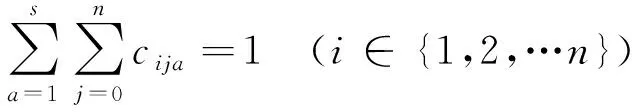
(14)

(15)

(16)

(17)

(18)

式中：Z为总补给成本；q为补给船每行驶一个单位距离所需要的运输成本；H为补给船所能够行驶的最远距离；Q为补给船所能够允许的最大装载量；s为补给船总数量；g为补给船的每一单位装卸所需要的成本；n为需要补给船给其补给的渔船数量；na为补给船a服务的渔船数量。

式(8)为目标函数，由补给船运输成本、装卸成本和惩罚成本组成；式(9)为每艘补给船的最远运输距离限制；式(10)为每艘补给船装载的生产生活物资总量不能超过补给船的最大载货量；式(11)为每艘补给船装载的渔获总量不能超过补给船的最大载货量；式(12)为补给船总的最大载货量限制；式(13)为等待补给的渔船数量限制；式(14)、式(15)为一艘渔船由且仅由一艘补给船提供补给；式(16)为补给船的航行路线构成一个闭环；式(17)为补给船a到达渔船j位置所用的时间；式(18)为对决策变量cija进行约束。

2 模型算法设计

遗传算法是一种典型的迭代算法，在实际运用中会出现局部搜索能力较差，容易早熟的现象。笔者把Tent混沌映射与遗传算法相结合，构造改进遗传算法，改变传统遗传算法群体适应值差别较大的现象。

2.1 编码方法

采用简单直观的自然数编码方法，以“0”表示补给船的出发地，n个自然数(1,2,…n)表示n个等待补给的渔船，一个染色体表示一个解决方案。

2.2 初始化种群

利用Tent混沌映射对种群进行初始化。利用Tent映射式(19)对其进行混沌扰动，产生混沌变量，然后根据式(20)将其映射到所要优化变量的取值范围内并取整，选择相应个体作为初始种群[9-10]。

(19)

gij=|1+(n-1)xij|,i=1,2,…S；j=1,2,…n

(20)

2.3 计算生产生活物资需求量和渔获卸载量

当初始种群确定后，由式(6)、式(7)计算每艘待补给渔船在该条航线中的生产生活物资实际需求量和渔获卸载量。

2.4 确定适应度函数

在确定适应度函数时，由于目标函数Z要求取最小值，且适应度越大越好，因此将目标函数值的倒数定位为适应度函数。

2.5 遗传操作

遗传操作包括选择操作、交叉操作和变异操作。一是选择操作，笔者采用轮盘赌选择法；二是交叉操作，采用部分匹配交叉法进行交叉操作，随机在父代个体选择一个区域进行互换；三是变异操作，采用逆转变异法，在准备变异的父代个体随机选定变异区域进行逆转操作，从而形成一个新的基因串。

2.6 终止条件

采用设定最大进化代数的方法作为终止准则。

3 算例分析

我国通常由10～40艘远洋渔船组成一定规模的船队，进行远洋捕捞作业。为此，选取某一时刻，有18艘远洋渔船需要补给船为其开展补给作业，此时有4艘补给船可以参与此次补给任务。每艘补给船的载货量Q均为3 500 t，补给船可以航行的最远距离H为5 000海里，经济航速v0为15 kn，每行驶一海里所需要成本为130元，单位装卸成本为7.6元/吨。通过对渔船单小时所捕鱼货价值、生产生活物资消耗等各种费用预估，计算单小时惩罚成本为210元。渔船和补给船的其它参数如表1、表2。

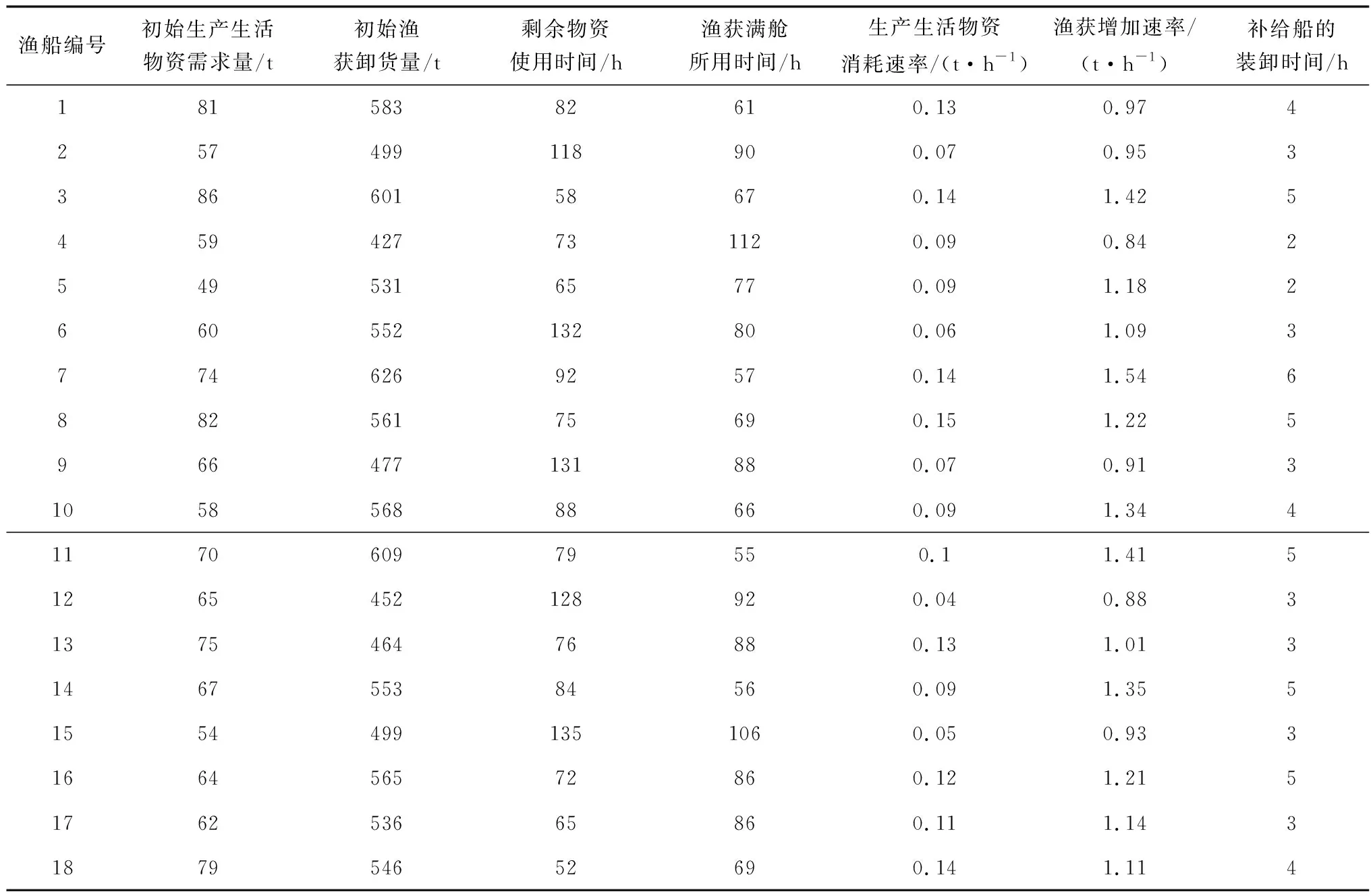
表1 等待补给的渔船参数Table 1 Fishing boat parameters waiting for replenishment

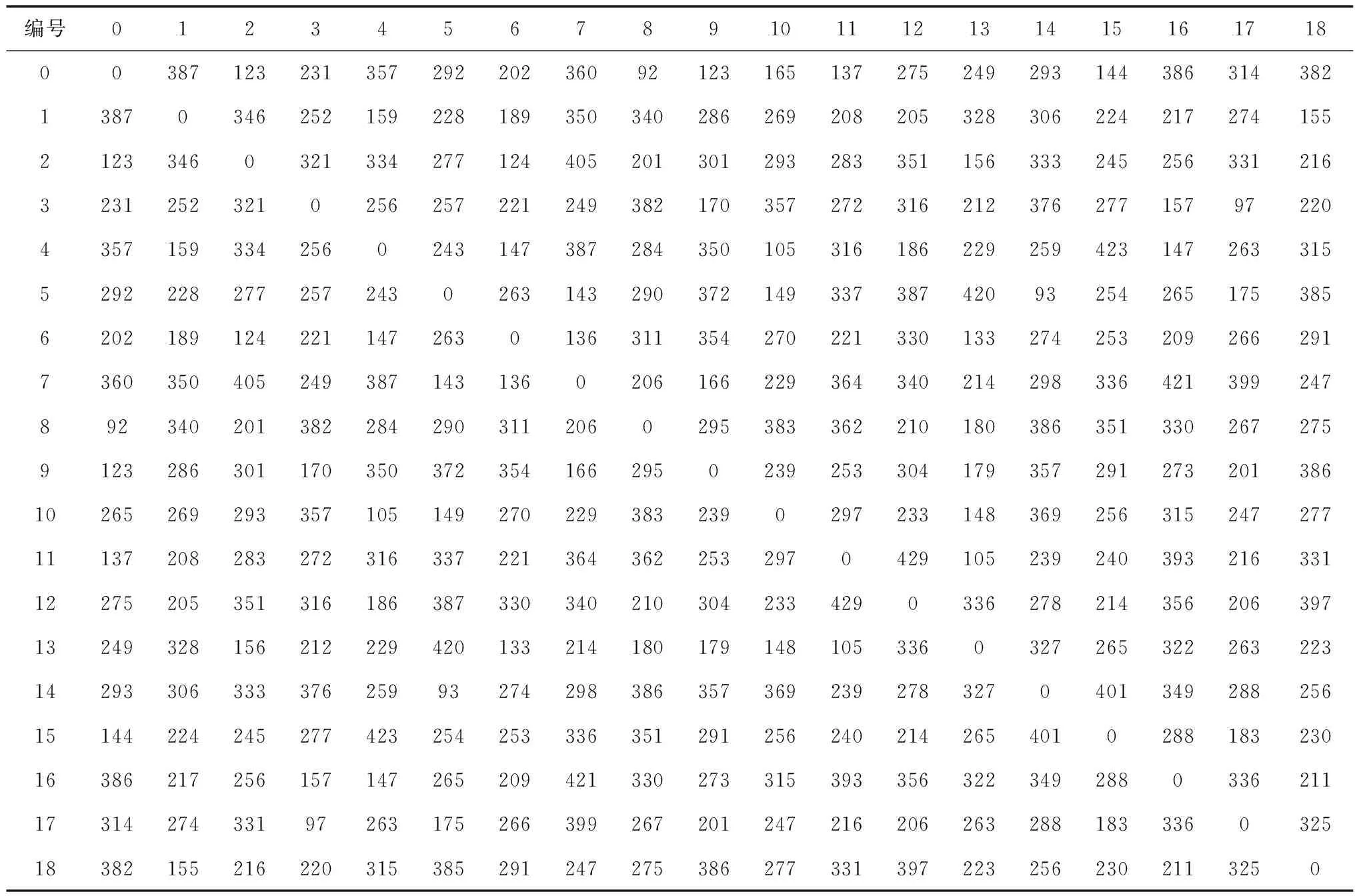
表2 补给船出发地与渔船之间的距离Table 2 Distance between the starting point of the replenishment ship and the fishing boat 海里

通过MATLAB R2016a编程实现改进遗传算法，在算法计算中，种群规模设置为200代，交叉概率为0.8，变异概率为0.1，迭代次数为800代，运行迭代结果如图3。

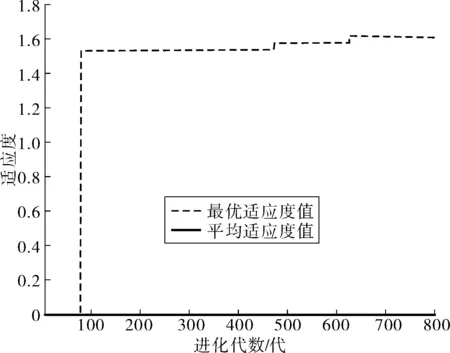
图3 改进遗传算法适应度曲线Fig. 3 Improved genetic algorithm fitness curve

此次任务共需向远洋渔船补给生产生活物资1 291 t，返回时共装载10 632 t渔获物，补给总成本为61.694 1万元。

补给船Ⅰ的补给顺序为0—12—8—16—2—0，出发时共需载渔船所需生产生活物资287 t，返航时共载回渔获2 292 t，返航装载率为65.49%，装载率较低。因此在进行补给时，可以考虑使用多种船型，让载货量低的补给船服务节点少的航线。

补给船Ⅱ的补给顺序为0—3—17—11—14—0，出发时共需载渔船所需生产生活物资300 t，返航时共载回渔获2 502 t，返航装载率为71.49%。

补给船航线规划方案如表3。

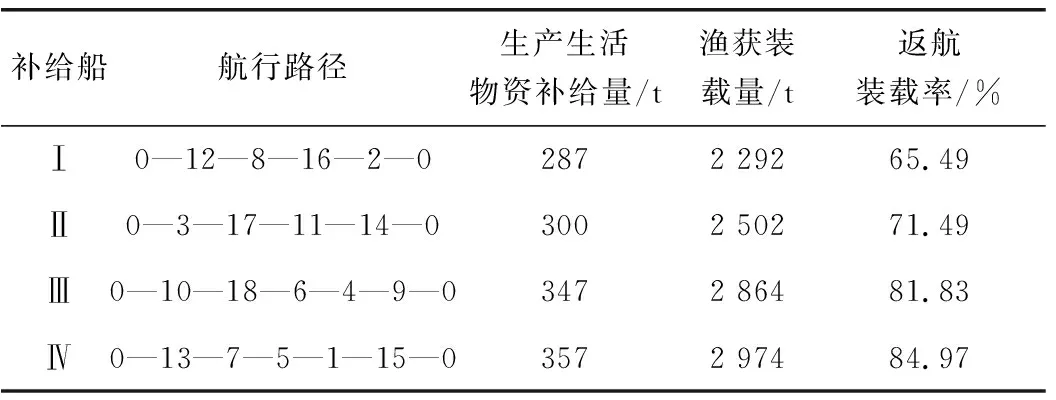
表3 补给船航线规划方案Table 3 Route planning of replenishment ship

补给船Ⅲ的补给顺序为0—10—18—6—4—9—0，出发时共需载渔船所需生产生活物资347 t，返航时共载回渔获2 864 t，返航装载率为81.83%。

补给船Ⅳ的补给顺序为0—13—7—5—1—15—0，出发时共需载渔船所需生产生活物资357 t，返航时共载回渔获2 974 t，返航装载率为84.97%。

4 结 语

在满足远洋渔船正常补给需求的条件下，补给船到达时间的长短将直接影响到补给成本和补给效率，因此合理安排补给方案，既能保证渔船作业的正常进行，也有利于提高补给船的补给效率。在分析补给成本的基础上，建立混合时间窗下的惩罚成本函数以及生产生活物资实际消耗量和渔获增长量函数，构建补给船航线规划模型，最后利用改进遗传算法进行求解，得出补给成本较低的优化方案，有助于提升补给船的补给效率。