金属波纹管内液氧流动的涡脱落特性仿真

2021-01-18朱景文周卫雪

上海航天 2020年6期

严伟，朱景文，周卫雪

（1.蓝箭航天空间科技股份有限公司，北京 100176；2.北京航天长征飞行器研究所，北京 100076）

0 引言

金属波纹管是一种具有褶合轮廓的柔性管材，在管路系统中通过褶合处的变形补偿管道连接处的相互位移，同时吸收振动能量。这使得其在保持局部刚性的同时，整体又具有柔韧性，因此，被广泛应用于液体火箭发动机的推进剂输送系统中。

液体火箭发动机常采用低温介质液氧作为助燃剂。当液氧在波纹管中输送时，流动状态通常是复杂的非定常湍流。同时，受褶合区域复杂几何的影响，液氧的流动会呈现出一定的周期性，进而诱导波纹管结构发生振动［1-2］。流体诱导振动的强度通常不大，影响可忽略，但如果振动频率接近波纹管固有频率，将引起结构共振，此时迅速增大的交变应力会在很短时间内令波纹管疲劳失效［3-5］。

美国早在20 世纪60 年代就开展了波纹管流体诱导振动的相关研究。在土星5 运载器第2 次飞行期间，其中1 台2 级J-2 发动机发生故障导致提前关机；同一次飞行，3 级的J-2 发动机在地球轨道上起动失败。这些异常最后查明是由于流体诱导振动导致波纹管疲劳失效引起的。这些失效案例促使美国对流体诱导波纹管振动问题进行了广泛研究，调查分析了超过50 个不同种类的挠性软管和管路样本［6］。

早期的流动可视化试验，观察到波纹管褶合处有漩涡不断脱落，确认了流体在波纹管内壁的涡脱落是诱导振动的原因。基于涡脱落理论，美国国家航空航天局（NASA）建立了流体诱导波纹管振动的数学模型，提出了估算波纹管在给定几何尺寸和来流速度下的流体诱导振动应力的半经验方法。该方法将波纹管每半个褶合等效为集中质量，各集中质量之间采用弹簧连接，通过计算波纹管固有频率以及涡脱落频率，求得激起的波纹管模态阶数。在此基础上估算波纹管应力，同时编制了计算波纹管流体诱导交变应力的计算程序。该方法对高压挠性软管以及刚度较大的自由金属波纹管的预测较为准确。应用该方法对土星/阿波罗运载器上所有使用的波纹管进行了计算，以判断流体诱导振动问题是否存在。此后，NASA 完善了试验数据，进一步修正了模型中的中的系数，提高了精度［7］。

在国内，李中来等［8］、马明等［9］、罗宏瀚［10］分别针对波纹管的疲劳失效问题展开了研究。其中，罗宏瀚基于商用软件ANSYS 建立了流体诱导波纹管振动的计算模型，比较研究了波纹管参数、流动等性质对振动的影响，定性分析了不同条件下振动的特征，并根据计算结果提出了波纹管流固耦合的减振方法。

本文利用二维大涡模拟模型，对波纹管内液氧流动进行非定常数值仿真，发展了波纹管流动的涡脱落幅频特性预测方法；研究了液氧流动速度、波纹管几何对涡脱落频率的影响，并归纳出了计算涡脱落频率的经验式，弥补了已有研究在工程适用性上的不足。

1 数学模型

液氧在液体火箭发动机波纹管内的流动本质上是一种复杂的三维、非定常、高雷诺数湍流。由于波纹管的结构具有轴对称性（如图1 所示），液氧内部的流动可近似视为轴对称流动，故此可将三维流动问题简化为二维。

同时引入流动不可压假设，并忽略重力和热传导影响，则可用如下二维、黏性、不可压控制方程来描述波纹管内液氧的流动。

连续方程为

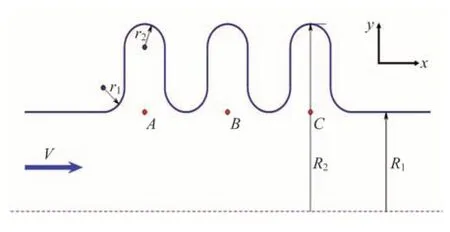
图1 波纹管几何模型Fig.1 Schematic diagram of bellows geometric model

x方向动量方程为

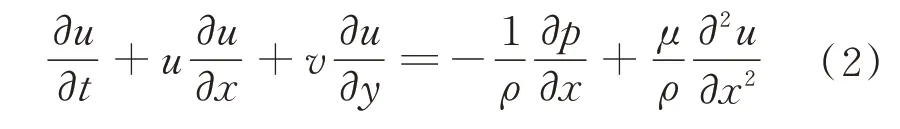
y方向动量方程为

式中：u、v分别为流动沿x、y方向的速度分量；p为压强；ρ、μ分别为液氧的密度和动力黏性系数；t为时间。

本文采用大涡模拟模型来描述波纹管内的湍流运动。它的基本思想为：大尺度脉动（或大尺度湍流涡旋）的结构依赖于个别的流动问题，不存在通用模型，因此，直接通过求解Navier-Stokes 方程获得；而小尺度脉动近似各向同性，其对大尺度运动的作用可以使用模型假设［11］。然而，大涡模拟是针对三维问题提出的，为了能在二维问题中应用该模型，本文参考文献［12］中建立的二维大涡模拟格式进行数值计算。

2 计算方法

2.1 网格划分

采用有限容积法对计算区域进行离散，生成如图2 所示的结构化网格，并且对近壁面处网格进行加密。在波纹管褶合区域内，使用C 型网格。

图2 网格划分示意图Fig.2 Schematic diagram of meshing

2.2 定解条件

在进口截面给定速度边界条件

在出口截面给定压力边界条件

在壁面处给定无滑移固壁边界

在对称边界给定

式中：下标inn 为进口截面；out 为出口截面；wall 为固壁；axis 为对称轴。初始条件给定波纹管褶合内速度为零，其余部分同进口边界条件。

3 仿真结果及分析

3.1 仿真结果

进口速度uinn=30 m/s 时，流动充分发展后在通道褶合附近8 个不同时刻的速度云图如图3 所示，时间差Δt=1.2×10-4s。由图可知：主流区的速度波动较小；当液氧流经褶合的上坡侧时，流道扩张导致速度下降，并较大的旋涡产生、脱落；当液氧流经褶合的下坡侧时，流道收缩，速度增大，并且受回流的影响，之前在上坡侧出现的脱落涡被卷吸进入褶合内部，与褶合内原有的涡相互作用。该过程不断重复，诱导波纹管结构发生振动，振动的频率等于褶合上坡侧的涡脱落频率。

图3 不同时刻波纹管内的速度分布（uinn=30 m/s）Fig.3 Contours of velocity magnitude（uinn=30 m/s）at different time in the bellows

为了定量分析涡脱落的频率，在C点（见图1 标注）设置数字探针，监控其速度的脉动。当流动充分发展后，截取0.1 s 之内的速度信号如图4 所示。横坐标表示时间，纵坐标表示C点的速度大小。由图4 可见，C点速度随时间高频振荡，平均速度为21.57 m/s。

对速度-时间信号进行快速傅里叶分析（FFT），得到其幅频特性如图5 所示。横坐标表示信号的频率成分，纵坐标表示相应频率下的振动幅值。

图4 C 点速度信号（uinn=30 m/s）Fig.4 Velocity signal at point C（uinn=30 m/s）

图5 C 点速度信号的幅频特性（uinn=30 m/s）Fig.5 Amplitude-frequency characteristic of the velocity signal at point C（uinn=30 m/s）

由图可知：图4 所示速度-时间信号的基频为2 030 Hz，对应速度分量波动的幅值为0.684 2 m/s，约占平均速度的3%；二阶频率对应分量的波动幅值为0.225 7 m/s，约占平均速度的1%；三阶及其以上频率分量强度很小，可忽略。

为了分析流动速度对涡脱落频率的影响，本文设计了多组对比算例，对不同进口速度uinn下的流场进行了仿真，并分别对C点的速度-时间信号进行FFT 处理，不同进口速度下的基频见表1。可见，涡脱落运动的基频与液氧流动速度近似成正比，液氧流动速度越大，涡脱落频率越高。

表1 不同uinn下C 点速度波动的基频Tab.1 Base frequency of C-point velocity signal at different uinn

如图3 所示，涡脱落运动的动态过程，涡脱落频率除了与液氧流动速度有关，还可能受波纹管褶合处几何参数的影响。

本文基于控制变量法，在波纹管进口速度不变的条件下，分别研究了r1、r2（如图1 所示）对涡脱落频率的影响。

某一较小r1、进口速度为30 m/s 时，波纹管内液氧流动充分发展后，在通道褶合附近8 个不同时刻的涡量云图如图6 所示，时间差Δt=1.0×10-4s。从涡量云图上也可以观察到周期性的涡脱落运动，同时，由于褶合上坡侧曲率半径r1较小（相对于图3所示），加快了涡脱落的过程。

图6 某较小r1条件下不同时刻波纹管内的涡量分布Fig.6 Contours of vorticity under a small r1 at different time in the bellows

对不同r1、r2下C点的速度-时间信号分别进行FFT 处理，得到速度波动的基频与波纹管r1、r2的关系，结果见表2。其中，r0为特征半径，利用它对r1、r2进行无量纲处理。由表2 可见，r1、r2越大，速度波动的基频越小，意味着涡脱落频率随r1、r2增大而减小。

表2 不同r1、r2下C 点速度信号的基频Tab.2 Base frequency of C-point velocity signal at different r1，r2

3.2 结果分析

综上所述，波纹管内涡脱落运动的基频fst与进口速度uinn正相关，与r1、r2负相关，据此将fst与uinn、r1、r2之间的函数关系归纳为如下形式：

基于式（4），对表1 和表2 中数据进行最小二乘分析，确定比例系数ξ=0.26。

分析经验式（4）可知，当r1、r2一定时，fst与uinn成正比。经验式计算值与表1 中仿真数据对比如图7所示，数据点与拟合直线贴合较好，表明经验式正确反映了波纹管内涡脱落运动的基频与流动速度之间的关系。

图7 经验式计算值与表1 数据对比Fig.7 Comparison of empirical formula calculations with Tab.1

当uinn一定时，fst与r1、r2之和成反比。经验式计算值与表2 中仿真数据对比如图8 所示。图中曲面表示uinn=30 m/s 时fst与r1、r2之间的函数。从图中可以看出，表2 中数据基本上均匀分布在曲面两侧，且与函数曲面贴合较好，这表明经验式合理反映了波纹管内涡脱落运动的基频与r1、r2之间的关系。