无刷直流电机的模型预测与反演控制

谭天乐，尹俊雄，周恒杰，郑翰清

（1.上海航天控制技术研究所，上海 201109；2.上海市空间智能控制技术重点实验室，上海 201109）

0 引言

无刷直流电机（Brushless DC Motor，BLDCM）因结构简单、运行高效可靠、便于控制而得到广泛应用。转台、数控机床、机器人等在各种负载工况和任务下的高精度、敏捷控制一直是国内外研究和应用中的关注热点。

关于无刷直流电机的控制方法，因为比例积分微分（Proportional Integral Derivative，PID）控制方法成熟、形式简单，所以工程中应用较多，并从控制精度、控制稳定度、控制快速性以及抗干扰能力等方面结合其他控制方法以提升性能。模糊控制［1-3］按照模糊规则调整参数，计算控制量，根据转速误差及其变化率设计模糊律，在线实时调节比例积分（Proportional Integral，PI）参数，具有较好的鲁棒性和动态稳态性，但通常需要先验知识和经验。鲁棒控制［4-6］根据参数的不确定性及干扰的摄动范围设计控制系统，适用于具有模型不确定和外部干扰摄动的情况。文献［5］运用线性矩阵不等式理论设计的H∞模糊控制器，使非线性系统对扰动具有较好的鲁棒性，但实时计算量大，不利于工程实现。自抗扰控制［7-9］不依赖于模型，算法简单、超调低，收敛快且精度高，鲁棒性较强，但需整定的参数较多。滑模变结构控制［10］可以在线调节以应对转动惯量和摩擦力的不确定性，对系统参数变化及外部扰动不敏感，具有较强的鲁棒性与自适应性，可以实现较好的动态控制效果，但存在抖振现象，需要采用高阶滑模［11］、自适应趋近律［12-13］等方法削弱抖振。神经网络控制［14-15］可通过学习优化PID 参数，常结合遗传算法［16］等以提高计算效率或避免局部最优，但需要解决可解释性和实时性问题，通常需要离线进行数据的训练以得到较优的参数值。预测控制［17-20］采用模型预测、滚动优化和反馈校正，通过目标函数优化得到控制量，具有静差小、抗负载扰动强的特点，但系统性能依赖于目标函数的合理设计，且对于多步预测控制，计算量大，难以应用于要求快速性的伺服系统中。

以上预测控制之外的其他方法均在每个测控时刻获取系统当前状态信息，并与期望状态进行比较，计算当前的状态偏差，以当前的状态偏差为基础进行控制。控制器的设计基于系统的动力学方程，从系统稳定性分析的角度出发，考虑控制系统中的指标要求进行设计和参数选择，采用Lyapunov函数或者零极点分布等方法分析控制系统稳定性，证明系统在控制律的作用下，对于期望的状态是渐进稳定的，从而实现系统状态控制。常规的预测控制在预测未来的系统状态后，在控制器设计时大多以控制性能和代价建立目标函数，通过最优化方法，求取控制量，并不断迭代优化，对控制系统的分析和设计依然是基于系统的稳定性。

本文对BLDCM 的电气与机械特性进行了分析与建模。在数字控制系统中，采用模型预测的方法估计电机转速、转角的未来偏差。基于系统能控性和电机受控转动的状态变化规律，根据估计的状态偏差反演控制电流与电压指令，提出了BLDCM 转速控制以及转速、转角同步控制的模型预测与反演（Model Predictive and Inversive，MPI）控制方法。不同于对负载的在线辨识和干扰已知情况下的前馈补偿控制，本文基于电机负载及外部力矩干扰对系统状态的影响机理，根据状态偏差直接反演出负载/干扰补偿控制指令。最后，考虑工程实际情况中电机参数误差、系统状态测量误差和实时摩擦力的影响，本文仿真验证了MPI 控制方法的有效性。

1 电气与机械特性建模[21]

对于定子为三相对称星型连接绕组的BLDCM，其状态空间形式的电气特性方程为

式中：X1=[iaibic]T为状态变量，其中，ix|x=a，b，c为三相绕组中电流；U1=[uaubuc]T为控制输入，其中，ux|x=a，b，c为三相端电压值，

E=[eaebec]T，ex|x=a，b，c为三相反电势；R、L、M分别为每相绕组的电阻、电感与绕组间互感。

状态空间形式的机械特性方程为

式中：X2=[ω]为状态变量，ω为电机转速；U2=[iaibic]T为控制输入；W=[Tl]为负载转矩；相关矩阵为A2=[-Bf/J]；B2=K为反电势系数，fx(θe)|x=a，b，c为反电势波形函数，θe为转子电角度，，J为转子转动惯量。

电机参数K、J、Bf、R、L、M通常均为已知，三相电流、转速ω可以测量得到，反电势函数在每个控制周期中可通过电角度查表计算得出。

2 模型预测与反演控制律

2.1 转速控制

当采样周期T足够小时，近似认为三相端电压和反电势在一个测控周期内不变，对式（1）进行状态转移过程求解，得到

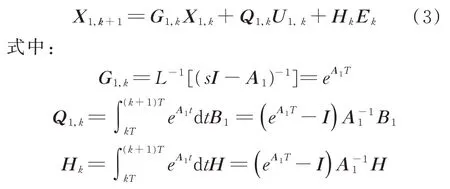
下标k、(k+1)分别为当前控制周期初始时刻和末端时刻系统状态；I为单位阵；Ek为当前周期的反电势；Hk为反电势作用常值矩阵。

由系统的能控性充要条件，易知

系统完全能控。

V为相应维数的任意向量。取通解中的唯一最小二乘、最小范数解，得到控制电压为

同理，对式（2）进行状态转移过程求解，得

因为A2、P为常值，所以，G2，k、Pk为常值。对于下一测控采样时期望的电机转速设计控制电流为

系统在U21，k控制作用下，将会出现转速偏差为

设计负载补偿控制输入为

式中：kc为调节负载补偿的速度而引入的正值补偿系数。若负载力矩一直存在，则U22，k应始终维持，得到负载情况下控制器的输出为

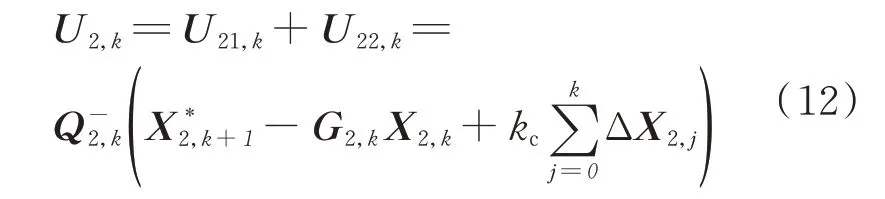
则在式（12）的控制作用下，系统逐步收敛到期望值。

2.2 转角与转速同步控制

在一些应用如切削加工中，对电机的转角、转速需要同步控制。

记电机转角为θ，则有=ω，离散形式为

以电机转角、转速X3=[θ ω]T作为状态变量，由式（8）和式（13）有

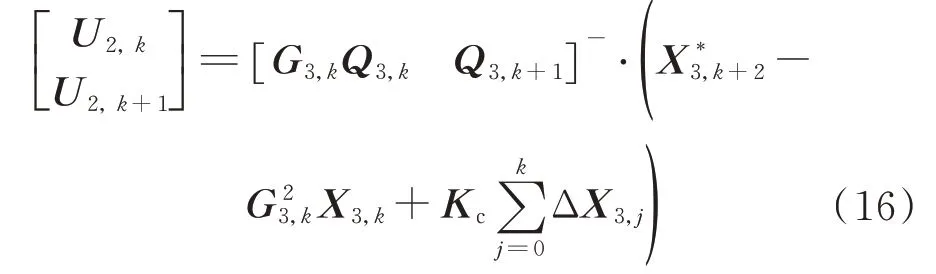
式中：Kc=diag([kc1kc2])，为二维正定对角矩阵，其中，kc1、kc2分别为调节角度、角速度控制误差补偿速度而引入的正值补偿系数。

取U2，k输出，下一控制周期中，重新计算并取相应的U2，k输出。

以上即为BLDCM 的模型预测与反演控制律。模型预测与控制反演控制是一种基于系统能控性分析的控制方法。不同于通过求取目标函数最优解进行控制的常规预测方法，该方法基于受控对象的运动学规律，预测和估计系统未来的状态偏差，基于外界作用对系统状态所产生控制作用的动力学规律，反向推演使得系统达到期望目标的控制量，设计状态转移的预测及反演控制器，从而实现系统状态的稳定跟踪。

3 仿真及分析

仿真所用电机参数见表1。

表1 电机参数Tab.1 Parameters of motor

考虑参数和测量误差：电流测量的比例误差0.05，常值误差0.05 A，噪声0.005 A；角度测量的常值误差0.002 8°，角度测量噪声0.001 7°，由码盘安装导致的角度测量误差-0.003°，角速度测量误差0.002 9(°)·s-1；控制电压输出误差3%。

电机控制周期T为0.001 s，在8 s 时加负载转矩2 N。同时仿真了工程上常用的三环PID 控制和文献［10］所提出的自适应鲁棒滑模控制方法以作比较，并考虑了实时摩擦力矩Ff为

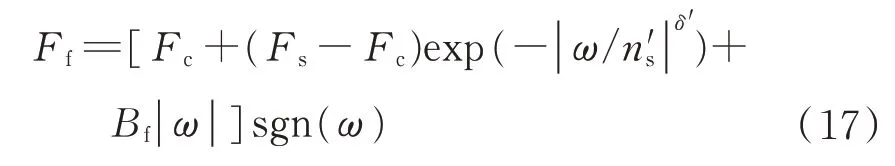
式中：库仑摩擦力矩Fc=4 N·m；最大静摩擦力矩Fs=5 N·m；临界Stribeck 速率=0.1 rad·s-1；经验参数δ′=2；ω为转子转速。

令电机转角指令为

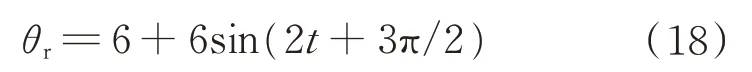
电机初始角位置θ0=0 rad，初始角速度ω0=0 rad·s-1。PID 控制参数为：位置环Pθ=100，Dθ=0.1；速度环Pω=50，Iω=40；电流环为Pi=2。仿真结果如图1 和图2 所示。

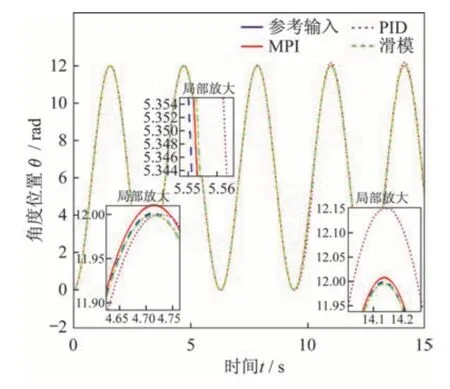
图1 角度跟踪Fig.1 Angle tracking

图2 角度跟踪误差Fig.2 Angle tracking error

在图1 和图2 中，PID 控制在负载加入后的角位置误差明显增大，而滑模控制对扰动的鲁棒性优于PID 控制，MPI 控制在负载加入前后的跟踪精度均较高，对恒值负载具有较好的鲁棒性，误差范围在±0.01 rad 内。

角速度跟踪效果如图3 和图4 所示。由图3 和图4 可知，MPI 控制在负载加入前后都能以较高精度、较平滑地跟踪输入，对负载扰动、摩擦力的鲁棒性较强。

若转角指令为从0 rad 到6 rad 并保持在6 rad 不变，并利用5 次多项式规划转角路径［23］，如图5 所示。由图5 知，MPI 控制的抗干扰能力优于PID 控制，滑模控制偏差较大，因而滑模控制器更适用于参考速度不为零的动态控制过程。

图3 角速度跟踪Fig.3 Angular speed tracking

图4 角速度跟踪误差Fig.4 Angular speed tracking error

图5 角度保持比较Fig.5 Comparison of angle keeping

仿真表明，MPI 控制方法及设计的干扰补偿可以使系统具有较好的动态与静态性能，既能跟踪实时变化的状态轨迹，也能使系统平稳转移到某个状态并保持稳定，且干扰补偿无需辨识扰动，只利用转角转速信息就能达到较好的抗扰动控制效果。

4 结束语

本文在电气与机械特性分析建模基础上，建立了无刷直流电机的离散时间控制系统模型，通过模型外推的方法预测和估计控制的偏差，根据电机受控转动的规律反演电压、电流控制指令，提出了无刷直流电机的模型预测反演控制方法。与PID 控制、滑模控制的对比仿真表明，考虑电源误差、电机参数误差、传感器测量误差等工程实际情况，MPI方法具有较好控制精度、控制鲁棒性以及快速响应能力。