双片消隙齿轮动力学建模与参数影响分析
2021-01-18刘伟平穆京京刘宽耀庄春跃
刘伟平,穆京京,刘宽耀,庄春跃
(1.上海无线电设备研究所,上海 201109;2.中国航天科技集团有限公司 研究发展部,北京 100048)
0 引言
雷达导引头伺服系统作为导弹的跟踪指向机构,根据天线测角偏差,控制天线转动实现目标跟踪,其指向精度、稳定性直接影响导弹的命中精度。雷达导引头伺服系统为提高其传动精度一般采用双片齿轮消隙[1-3]的方式消除回程误差,能够有效消除齿轮传动过程中齿侧间隙对传动精度及系统稳定性的影响,因其结构紧凑也广泛应用于其他航天精密伺服机构,如机载雷达天线[4]、光电稳定平台等。
国内外已有较多学者针对消隙齿轮动力学特性开展了研究。国内国防科学技术大学多位学者对消隙齿轮伺服系统进行了仿真分析,开展了消隙齿轮机构综合啮合刚度、振动响应、谐振特性等方面的研究[5-8]。国外IMASAKI 等[9]提出了一种具有消隙齿轮传动关节的工业机器手控制方法,建立了一种具有三段柔性连接特性的消隙齿轮近似刚度模型。ALLAN 等[10]建立了考虑了电机和负载的消隙齿轮传动系统模型,提出了计算消隙弹簧最小预紧力矩的方法。KWON 等[11]建立了消隙齿轮传动系统模型,将双片齿非线性刚度模型转换为线性刚度模型,研究了系统的频域响应特性。
上述研究中,在建模时对消隙齿轮的啮合刚度的处理较多采用将轮齿刚度与扭簧刚度进行分段等效的方法,而扭簧预紧力作为齿轮系统的内力则无法在模型中体现,其产生的额外的齿面载荷及摩擦力矩对系统的动力学特性将有一定影响。因此,本文拟建立考虑时变啮合刚度及齿面摩擦的消隙齿轮动力学模型,分析扭簧预紧力矩及扭簧刚度对系统动力学特性的影响。
1 消隙齿轮动力学建模
消隙齿轮示意图如图1 所示,齿轮1 与输入轴固连,齿轮2 和齿轮4 与输出轴固连,齿轮3 浮动安装,齿轮1 和齿轮3 通过扭簧连接,安装时齿轮1 与齿轮3 扭转一定角度后与齿轮2、4 啮合,完成扭簧加载。通常情况下齿轮2、4 为1 个齿轮,这里为了便于分析将其拆为2 个齿轮,两者通过一个较大刚度的圆柱段连接。
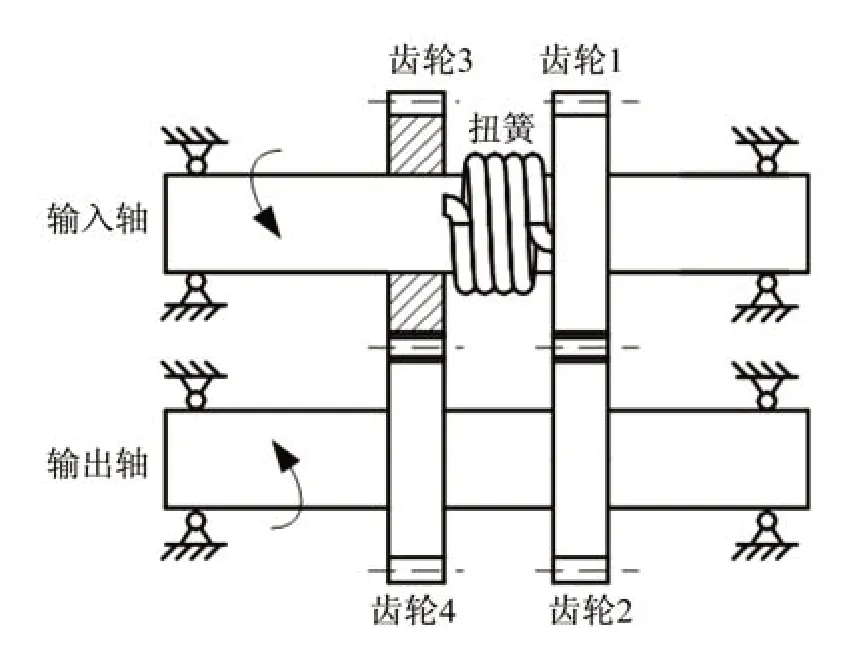
图1 消隙齿轮传动模型Fig.1 Model of anti-backlash gears
按图1 所示的方向运行,假设扭簧加载在齿轮1上的扭矩与转动方向相同,以两侧啮合副为研究对象进行受力分析,如图2 和图3 所示建立坐标系,其中x轴垂直于啮合平面,y轴沿着啮合平面竖直向上。每个齿轮包括x、y方向的平移及绕z轴扭转3个自由度,其中扭转方向以逆时针为正方向。图中:km1、km2、cm1、cm2分别表示齿轮1 和齿轮2、齿轮3和齿轮4 的啮合刚度和啮合阻尼;kix、kiy、cix、ciy表示齿轮i沿x、y方向的支撑刚度及支撑阻尼(i=1,2,3,4);bc为齿侧间隙;Ts1、Ts2分别为扭簧加载在齿轮1、3 和齿轮2、4 上的静态扭矩;Ti为输入扭矩;To为输出扭矩,根据扭矩与齿轮旋转方向的关系确定齿轮传动的主从关系。

图2 齿轮1 和齿轮2 啮合副受力分析Fig.2 Force analysis of gear1 and gear2

图3 齿轮3 和齿轮4 啮合副受力分析Fig.3 Force analysis of gear3 and gear4
上述模型具有12 个自由度,系统的广义位移阵列可表示为
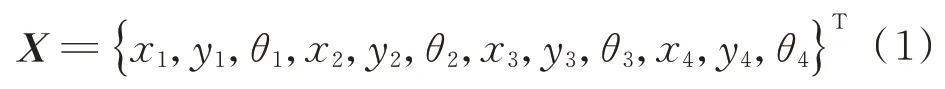
则两侧齿轮副沿啮合线的相对位移δ12、δ34可表示为

式中:rb1、rb2、rb3、rb4为各齿轮基圆半径;e1、e2为齿轮啮合误差。
左、右两端齿轮副的啮合力Fm1、Fm2可表示为
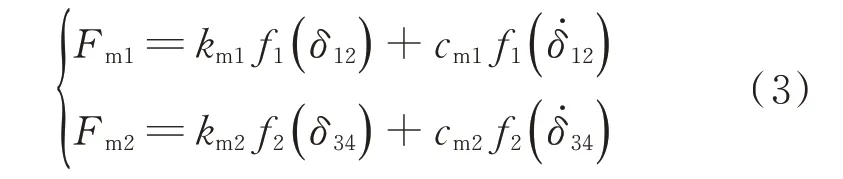
式中:km1、km2为时变啮合刚度,通过齿轮啮合有限元仿真获得[12];cm1、cm2为时变啮合阻尼,阻尼比选取范围为0.03~0.17;f1(δ)、f2(δ)为接触函数,由于消隙扭簧加载后,相邻两片齿轮是相反的齿面参与啮合,其初始啮合位置不同,表达式为

式中:bc为齿侧间隙。
根据上述分析,可推得双片齿消隙齿轮副动力学微分方程如下:

式中:k13x、k13y、kJ13、k24x、k24y、kJ24分别为两端齿轮x、y方向及扭转方向的刚度影响系数,其中kJ13即为扭簧的扭转刚度;c13x、c13y、cJ13、c24x、c24y、cJ24为两端齿轮x、y方向及扭转方向的阻尼影响系数;mi、Ii(i=1,2,3,4)为齿轮i的质量和转动惯量;ID、IL分别为输入端和输出端等效转动惯量;Ff1、Ff2为两侧齿轮副的齿面摩擦力;Tf1、Tf2、Tf3、Tf4为齿面摩擦力对齿轮1、2、3、4 的摩擦力矩。
摩擦力和摩擦力矩计算方法见文献[12]。
上述方程消除刚体位移后,进行量纲归一化,采用龙格库塔(Runge-Kutta)法[13]求解可求得系统的动态响应。
2 振动响应特性分析
某稳定平台传动机构采用1 级齿轮驱动,其齿轮参数见表1,主要分析扭簧预紧力及扭簧刚度对系统动态特性的影响。
啮合刚度通过有限元仿真获得,综合啮合刚度随时间变化曲线如图4 所示,啮合过程中单双齿交替产生的刚度变化是齿轮运行过程中主要的振动激励因素。图5 为表1 参数条件下的振动频域响应,振动能量主要集中在啮合频率110 Hz 及其倍频上。
在动力学模型进行仿真分析的过程中,只改变其中一个参数,而其他参数保持不变。通过改变扭簧预紧力矩、扭簧刚度,分析其对系统动态传动误差和谐振频率的影响,其中,动态传动误差为从动轮实际转角和理论转角之差。将角误差投影到啮合线转换为线位移误差,其表达式为式(2),误差产生来源于齿轮啮合误差、轮齿变形及振动引起的支撑变形等因素。

表1 模型算例参数Tab.1 Parameters of model example
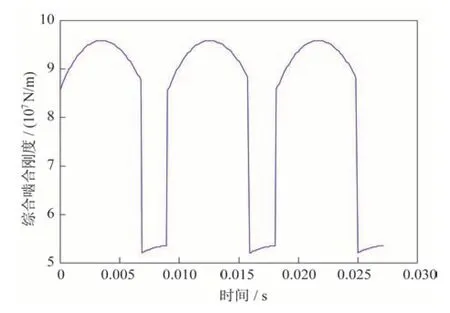
图4 综合啮合刚度曲线Fig.4 Curve of comprehensive meshing stiffness

图5 振动频域响应特性Fig.5 Frequency domain response of vibration
3 参数影响分析
消隙齿轮在扭簧加载后,输入轴正转和反转条件下,功率的传递路径是不同的。定义输入轴顺时针旋转时为正转,此时输入功率由齿轮1、2 传递至输出轴时,而反转时功率由齿轮1、扭簧、齿轮3、齿轮4 依次传递。因此,需分析这两种情况。
3.1 扭簧刚度对传动误差的影响
扭簧预紧力矩为0 时,两片驱动齿轮的正反齿面同时与从动轮啮合。以齿轮1 与齿轮2 接触时的位置为原点,扭簧加载后,齿轮组的刚度模型如图6所示。图中:θs为齿轮1 相对于齿轮2 产生静态弹性变形;θb为齿侧间隙对应的转角;齿轮1 与齿轮3 通过扭簧连接,其扭转刚度为kJ13;齿轮2 和齿轮4 通过一个大刚度的圆柱段相连,其扭转刚度为kJ24;两对齿的等效啮合扭转刚度为kJm1、kJm2。

图6 齿轮组的刚度模型Fig.6 Stiffness model of gear set
输入轴与齿轮1 固连,输出轴与齿轮2 固连,定义齿轮组等效刚度为齿轮1 和齿轮2 的相对扭转刚度,则等效扭转刚度表达式为
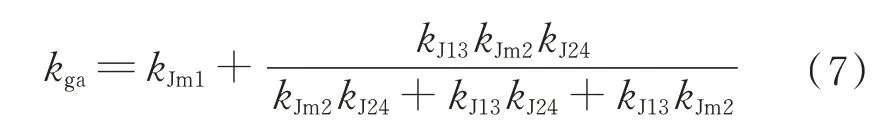
由于kJm1、kJm2、kJ24的数量级远大与kJ13,扭簧的刚度对整体等效刚度影响很小。
当齿轮反向转动,驱动力克服抵消扭簧加载力时,齿轮1 与齿轮2 脱离啮合,则等效扭转刚度表达式为

齿轮1 与齿轮2 脱离啮合后,齿轮继续反向转动θb,使得相反齿面参与啮合,齿轮组的刚度kgc为

综上可得,扭簧加载后齿轮组的等效刚度曲线如图7 所示,扭簧加载后由于预紧力的作用,齿轮组的工作点为图7 中的K(θs,Ts1)点。在该点附近,刚度曲线为线性,因此,在预紧力矩较为富裕的条件下,齿轮组可以始终工作在线性范围内,不会产生较大的回程误差。
正转、反转时不同扭簧刚度条件下齿轮的动态传动误差曲线,两条曲线基本重叠,如图8 所示。因扭簧预紧力矩存在,齿轮1 和齿轮2 之间基本始终处于接触状态,在扭簧预紧力矩较为富裕时,正转、反转条件下扭簧刚度的变化对传动误差影响较小。

图7 等效扭转刚度曲线Fig.7 Equivalent torsional stiffness curve

图8 扭簧刚度对齿轮传动误差的影响Fig.8 Influence of torsional spring stiffness on gear transmission error
3.2 扭簧预紧力矩对传动误差的影响
扭簧预紧力矩主要决定了齿轮组刚度曲线的线性范围,同时也引入了静态传递误差。正转时不同扭簧预紧力矩条件下齿轮的动态传动误差曲线如图9(a)所示。图中,正转条件下扭簧预紧力矩为0 N·m、4 N·m、8 N·m 时,齿轮啮合副传动误差曲线的平均值分别为-2.6 μm、-7.7 μm、-12.8 μm,最大振幅分别为1.7 μm、5.2 μm、8.8 μm,这是由于扭簧加载之后使得齿轮不仅要传递输入扭矩,还要承担扭簧加载的扭矩,使得齿面载荷增大,轮齿变形随之增大。反转条件下不同扭簧预紧力矩条件下齿轮的动态传动误差曲线如图9(b)所示,扭簧预紧力矩为0 N·m、4 N·m、8 N·m 时,齿轮啮合副传动误差曲线的平均值分别为102.4 μm、-2.6 μm、-7.7 μm,最大振幅分别为1.3 μm、2.4 μm、5.8 μm。在扭簧预紧力矩为0 N·m 时由于齿侧间隙的存在,反转时产生了较大的回程误差;扭簧加载之后,力矩通过加载齿轮一侧传递,消除了回程误差,但传动误差值随着加载力矩的增大而增大。
3.3 负载波动激励下扭簧预紧力矩及扭簧刚度对传动误差的影响
雷达导引头伺服机构一部分时间处于扫描搜索状态,其大部分工作时间处于跟踪或稳定在预定角度状态,而弹体飞行时的振动扰动会使得负载端产生一个惯性力矩,影响伺服机构的指向精度。假设某平台飞行过程中在伺服机构上将产生一个频率为80 Hz 加速度为15g的正弦振动,通过仿真计算得到该振动条件下系统的传动误差曲线如图10所示。其中,图10(a)中扭簧预紧力矩为0 N·m、2 N·m、4 N·m、8 N·m 时,齿轮啮合副传动误差曲线的平均值分别为51.5 μm、18.4 μm、-5.4 μm、-10.9 μm,最大振幅分别为78.9 μm、69.8 μm、23.3 μm、23.3 μm,图10(b)数据与图10(a)基本一致。

图9 扭簧预紧力矩对齿轮传动误差的影响Fig.9 Influence of pre-tightening torque of torsional spring on gear transmission error

图10 负载波动激励下齿轮动态传动误差Fig.10 Gear transmission error under load fluctuation excitation
在扭簧不加载的条件下,负载波动使得齿轮齿面脱离啮合,存在较大回程误差,且误差曲线不规律,传动系统存在不确定性。扭簧扭矩为2 N·m时,由于扭簧扭矩不足以克服振动引起的惯性力矩,仍存在齿面脱离啮合的情况,但由于扭簧的引入,其回程误差比扭簧不加载的情况下有所减小。扭簧扭矩为4 N·m 时,扭簧预紧力矩大于振动引起的惯性力矩,齿轮齿面不会脱离啮合,传动误差减小,但随着将扭簧扭矩增加到8 N·m 时,其传动误差曲线幅值已变化不大,继续增大预紧力矩对提高传动精度效果不明显。从图10(a)与图10(b)对比可见,扭簧刚度对传动误差曲线的影响较小,是由于一般用于加载的扭簧刚度数量级较小,在齿面脱离啮合后,扭簧无法在齿侧间隙行程范围内产生较大反扭矩。
3.4 扭簧预紧力矩及扭簧刚度对系统谐振频率的影响
由于传动系统动力学模型中包含齿侧间隙及齿面摩擦力等非线性因素,模型较为复杂,其谐振频率无法通过解析法直接求得,因此,采用模拟扫频的方式测试模型的频域特性。不同扭簧预紧力矩条件下系统的频域响应特性如图11 所示。图中:预紧力矩由2 N·m 增加到4 N·m 时,系统的谐振频率点由305 Hz 提高至345 Hz;增加到8 N·m 时,一阶谐振频率区域产生了两个尖峰,对应频率为325 Hz 和355 Hz;另外预紧力矩由2 N·m 依次增加到8 N·m,对应的一阶谐振频率的动态误差幅值为65.3 μm、46.4 μm、43.2 μm。因此,预紧力矩的增加对一阶谐振频率的动态误差幅值有一定的抑制,但二阶谐振频率的动态误差幅值以及非谐振区域的动态误差幅值增加。不同扭簧刚度条件下系统的频域响应特性如图12 所示。图中,不同扭簧刚度条件下的频率响应曲线基本相同。
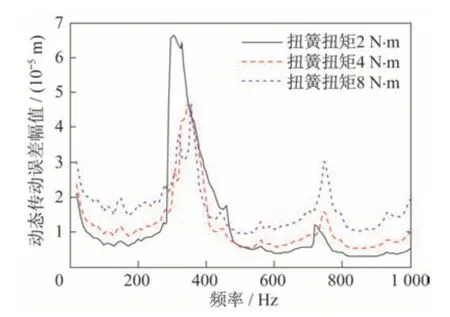
图11 扭簧预紧力矩对系统谐振频率影响Fig.11 Influence of pre-tightening torque of torsional spring on system resonance frequency

图12 扭簧刚度对系统谐振频率影响Fig.12 Influence of torsional spring stiffness on system resonance frequency
4 结束语
1)扭簧刚度对系统动态传动误差及谐振频率影响较小;
2)扭簧预紧力矩的增大有利于提高谐振频率,同时可以抑制一阶谐振幅值,降低负载波动对系统的影响,由于扭簧产生额外的载荷,扭簧预紧力矩的增加会增大系统动态传动误差,因此,在设计时需结合使用条件进行合理选择;
3)本研究为消隙齿轮关于扭簧设计提供了设计参考,在伺服控制系统设计中可对传动误差的仿真结果进行补偿修正以提高控制精度。
