基于ZAM-GTFR 和Hough Transform 的LFM 信号检测

2021-01-18曾小东曾德国

上海航天 2020年6期

曾小东，张薇，曾德国，祝俊

（电子科技大学电子工程学院，四川成都 611731）

0 引言

目前，低截获概率信号已经广泛应用于各种新体制雷达中，比较典型的如线性调频（Linear Fre‑quency Modulation，LFM）信号。LFM 信号具有很好的隐蔽性和抗干扰性，使得传统的基于功率峰值检测的雷达侦察设备很难完成对其的截获，需要研究新的检测方法来突破LFM 信号的低截获性。为此，近年来国内外众多学者针对LFM 信号的检测问题提出了许多新的处理方法。其中，比较典型的如BARBAROSSA［1］、孙晓昶等［2］、刘建成等［3］利用Wigner-Hough 变换（Wigner-Hough Transform，WHT）对LFM 信号进行检测，并分析了检测性能，对于多分量情况Wigner 的交叉项非常严重，导致Hough 变换无法正确提取时频的直线，故对多分量的检测性能不佳。KAY 等［4］、WOOD 等［5］、冉鑫等［6］使用Radon-Wigner 变换（Radon-Wigner Transform，RWT）分析了LFM 的检测，与WHT 一样存在交叉项问题；WANG 等［7］、JENNISON 等［8］、刘爱芳等［9］基于Radon-Ambiguity 变换（Radon-Ambiguity Trans‑form，RAT）同样完成了LFM 信号检测和参数估计，但由于Ambiguity 变换的时频聚集性有限，LFM 的检测概率受到一定影响。其他的方法还有基于Frac‑tional Fourier Transform（FFT）［10-12］和匹配傅里叶变换（Matched Fourier Transform，MFT）、多通道数字去斜和多通道自相关［13］等LFM 信号检测方法。

可以看出，LFM 信号的检测广泛地运用了时频分析的方法，ZAM-GTFR 作为一种典型的时频分布，具有诸多优点，如同时具备高的时间、频率分辨力，时域上维持了有限时间支撑，频域上加强了谱峰，且具备抑制交叉项的能力［14-15］。经过推导分析发现，ZAM-GTFR 对LFM 的调频斜率有极强的感知能力，能够用来分析LFM 信号的检测等问题。所以，本文综合前人的研究成果，针对LFM 的检测问题，提出了将ZAM-GTFR 和Hough 变换（Hough Transform，HT）相结合的方法，利用LFM 信号在ZAM-GTFR 变换后能够获得二维时间-频率分布的能量聚集特性，再进行HT 提取二维平面的瞬时频率直线特征，得到脉冲尖峰。通过仿真能够看出，在较低的信噪比下该方法仍然具有良好的检测性能。

1 问题描述

考虑高斯白噪声中，未知参量信号的检测问题，特别地，考虑观测时间为(-T/2，T/2)的接收信号r(t)。二元假设为

式中：w(t) 为零均值复高斯白噪声，即w(t)=wR(t)+jwI(t)，其中，wR(t)、wI(t)为相互独立的零均值实高斯白噪声，功率谱密度均为Pw(f)=N0/2；x(t；θ)为参量θ未知的复确定信号。

2 LFM 检测

对于大量的存储数据情况，广义似然比检测系统（Generalized Likelihood Ratio Test，GLRT）是最佳的检测系统，不同的判决准则只影响门限值γ的大小。因此，可得出如下检测准则：

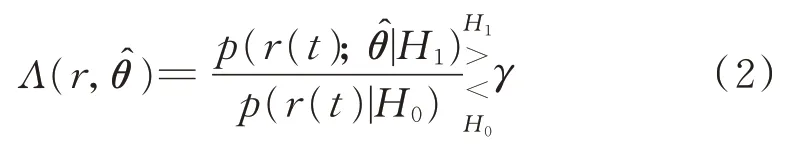
文献［4］利用RWT 分析了LFM 信号的检测问题。同样地，ZAM-GTFR 作为另一种Cohen 类时频分布，具备锥形核，可在一定程度上解决Wigner-Ville 分布（Wigner-Ville Distribution，WVD）的交叉项问题，所以ZAM-GTFR 也可用于LFM 信号检测且多分量情况下的检测性能更佳。详细的推导如下：

首先，WVD 的定义为

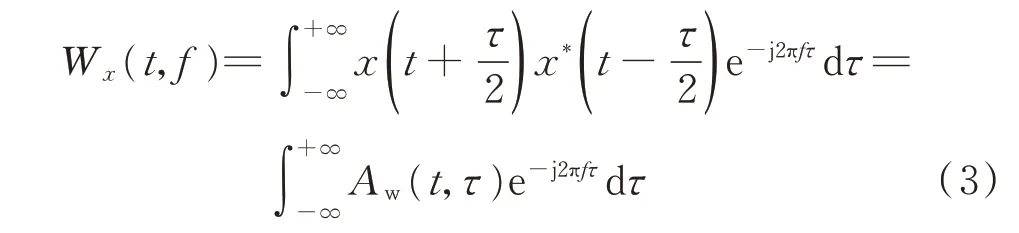
对于LFM 信号

式中：瞬时频率未知；θ=[fc，k，φ0]T包含了信号的未知参数；fc为起始频率；k为调频斜率；φ0为初相。

当观测时间T→∞时，

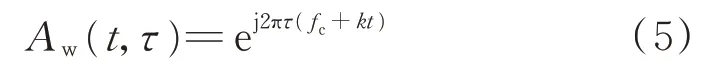
与初相φ0无关。

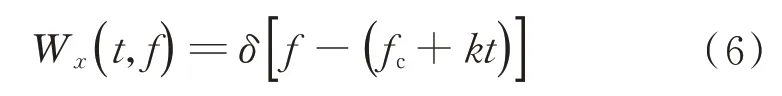
式中：δ[·]为狄拉克函数；f为频率。

ZAM-GTFR 的定义为

式中：Az(t，τ)为时间t的局部相关函数；g(τ)为加权函数。同样道理，对于LFM

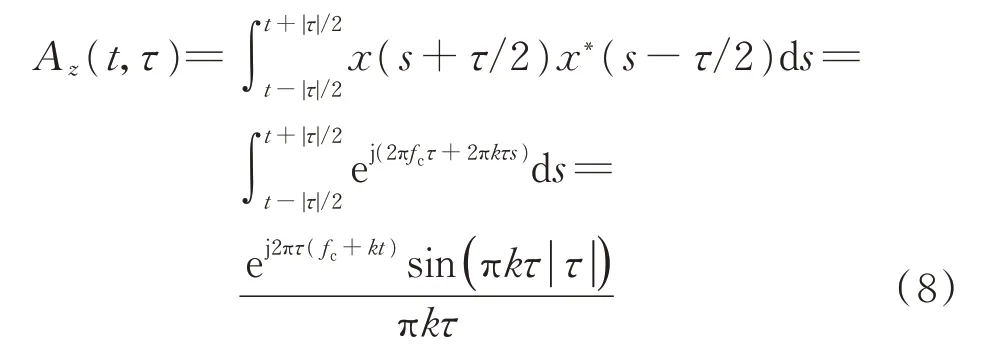
从式（8）可以看出，ZAM-GTFR 也与LFM 初相φ0无关。并且对比式（5）与式（8），我们发现，对于LFM 信号，ZAM-GTFR 相当于在WVD 的基础上，作了一个加窗处理。其中，窗函数为

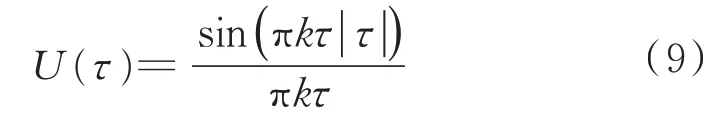
在频率域起到了平滑作用，可以在时频平面对频率方向的交叉项起到抑制的作用，所以ZAM-GTFR 在一定程度上克服了WVD 易受时频平面交叉项影响的缺点，特别是当处理数据量较大（多个调频时宽）时，优势可能更明显，特别适合多分量LFM 的信号处理。为了简化推导，假设加权函数g(τ)=1，则

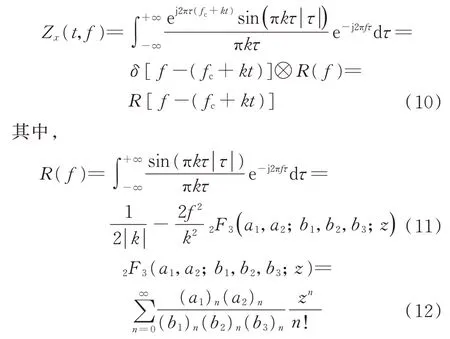
是广义超几何函数(λ)n=λ(λ+1)(λ+2)…(λ+n-1)，(λ)0=1，a1=1/2，a2=1，b1=3/4，b2=5/4，b3=3/2，z=-(π2f4)/(4k2)［16］。

根据文献［4］，有如下的GLRT 检测准则：

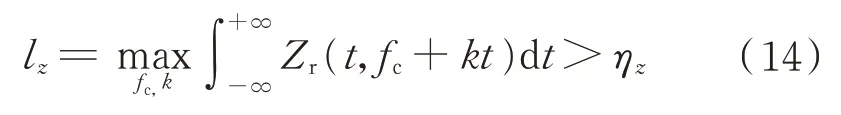
所以，由式（14）可知，对于LFM 信号的检测，可以分为以下几个步骤：

步骤1对截获的信号计算其ZAM-GTFR分布；

步骤2沿ZAM-GTFR 后时频平面上的所有直线做积分；

步骤3用最大的积分结果与指定的门限ηz做比较。若超过门限，则表明假设H1成立，有信号存在。

对于步骤2 的积分处理，有许多变换可以实现，如Radon 变换、Hough 变换等。本文拟采用Hough 变换，因为Hough 变换可以将平面里的直线映射为另一个二维平面的一个点，其实质是一个坐标变换，用一个新的2-D 坐标系(ρ，θ)替代原（t，f）。具体的变换关系为

对式（15）稍加整理可得

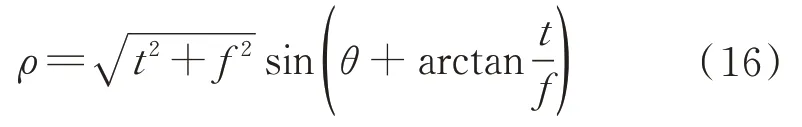
对于（t，f）平面上的任意一点，t、f为某常数，(ρ，θ)平面有一个与之对应的正弦曲线。一方面，如果在（t，f）上有一条直线，从该直线上的各点映射到(ρ，θ)的各正弦曲线将如积分一般，相交于一点，假设映射过程保持强度不变，则将在(ρ，θ)平面产生一个尖锐的峰值［17］；另一方面，随机噪声分布在整个平面上，因此，映射后的各正弦曲线不能相交形成一个尖峰。

3 性能分析

3.1 交叉项与计算量分析

为了分析ZAM-GTFR 时频分布的交叉项影响，常常以多分量音调信号

为考察对象。其中，f1、f2为信号p(t)的两个不同载频。文献［17］指出，p(t)的ZAM-GTFR 由信号项和交叉项组成：

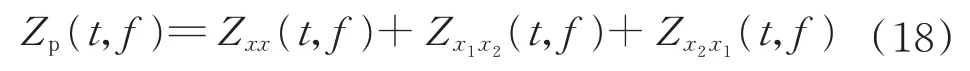
式中：信号项为

式中：L(f)为|τ|的傅里叶变换。

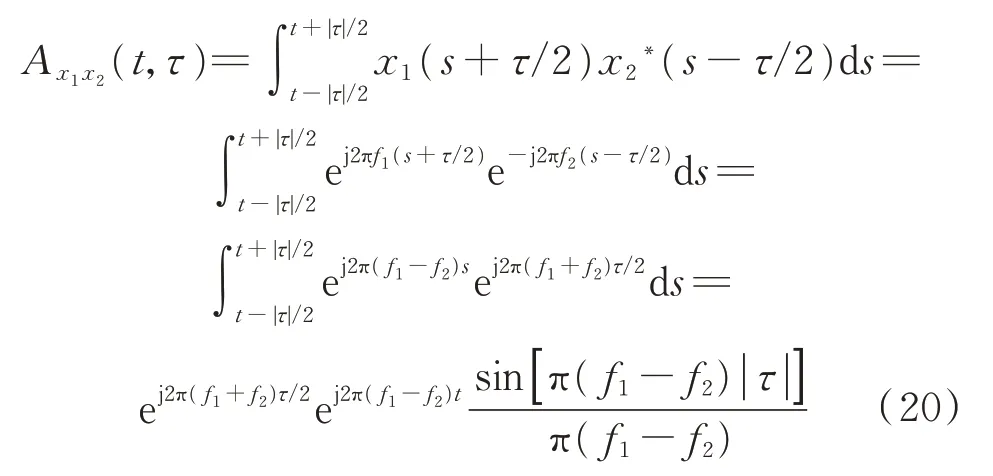
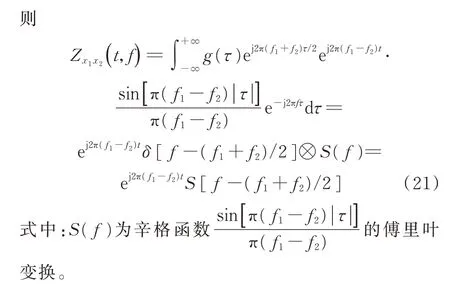
为了将本文算法应用于实际系统，考察ZAMGTFR 的计算量，假设L为频率点数，L=(M-1)/2，M为窗长。离散形式的ZAM-GTFR 等效为离散傅里叶变换取实部，所以可由基-2 的快速傅里叶变换（FFT）实现［14］。故计算一次ZAM-GTFR 需要（L/2）log2L次复数乘法和Llog2L次复数加法。

3.2 仿真结果

为了验证本文算法的有效性，做了如下的仿真。

仿真1实验中，采样频率fs为200 MHz，信号持续时间为T=3 μs，全频段信噪比为5 dB，LFM 分量1 的起始频率fc1=10 MHz，带宽B1=10 MHz，分量2 的起始频率fc2=15 MHz，带宽B2=20 MHz。仿真结果如图1～图3 所示。

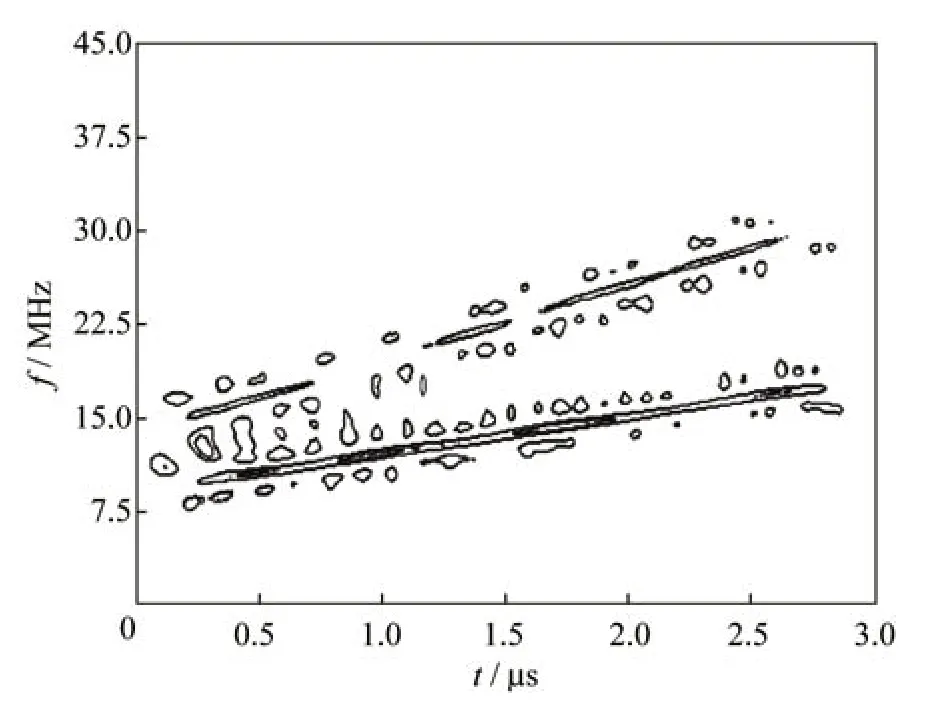
图1 加噪LFM 的ZAM-GTFRFig.1 ZAM-GTFR of LFM with noise

图2 高斯白噪声的ZAM-GTFRFig.2 ZAM-GTFR of Gaussian white noise

图3 信号ZAM-GTFR 的HF 值Fig.3 HF value of the signal ZAM-GTFR

仿真2实验中，采样频率fs为200 MHz，信号持续时间为T=5.12 μs，全频段信噪比为-5 dB到+5 dB，LFM 的起始频率fc=10 MHz，带宽B=10 MHz，与文献［1-3］提出的WHT 和相关法做了对比分析。仿真结果如图4 所示。

图4 LFM 的检测概率Fig.4 Detection probability of LFM

由图1 和图2 可知，ZAM-GTFR 很好地反映了LFM 信号的瞬时频率信息，且对于多分量信号而言能有效抑制交叉项的影响。图3 即进一步利用HT提取LFM 信号ZAM-GTFR 后的特征参数，可以看出在时频面上出现瞬时频率直线条件下，HT 变换后将对应出现一个明显的尖峰，且峰值的个数代表了LFM 分量的个数。

由图4 可知，在相同的检测准则下，由于ZAMGTFR 的U(τ)=sin(πkτ|τ|)/πkτ加窗效应，相对于WVD 而言，能够有效降低噪声对信号检测的影响，使得基于ZAM-GTFR 和HT 的检测方法在低信噪比下性能优于WHT，能够提高大约1 dB 的信噪比。同时，相关法信号处理速度快，适合实时处理，但是在低信噪比环境下，检测概率大大下降。