卫星遥测数据短时CEEMDAN-PSO-ELM预测模型

朱昶文，党建成，周 军

（上海卫星工程研究所，上海 201109）

0 引言

卫星在轨运行时，各个分系统传下的大量遥测数据是判断卫星运行状态是否正常的重要依据，也是进行卫星故障预测的重要前提。如何利用卫星的遥测数据进行精确预测，是航天器故障预测和健康管理（Prognosticand Health Management，PHM）的关键技术之一［1～2］。

目前，预测技术在航天领域已有一些研究。文献［3］基于灰色预测模型，利用相似性原理和新陈代谢原理，建立卫星遥测数据的新息灰预测模型，但该方法对于变化较剧烈的遥测序列，误差较大。文献［4］提出一种动态ARMA 建模方法，该方法根据所建立的适应度进行序列分割，不断更新模型，实现动态ARMA 预测，但该方法在序列中拐点预测误差较大。文献［5］提出一种基于PSO-SVR 的卫星姿态预测模型，利用PSO 算法优化SVR 模型，并应用在某卫星关键参数偏航角预测中，SVR 模型虽具有良好的非线性拟合能力，但精度依赖于参数是否准确。文献［6］提出根据遥测数据特征采用基于X-11 的数据分解算法进行分解，再利用不同的预测算法分别进行预测。

目前卫星遥测预测的研究存在对非线性遥测参数预测准确度不够或对参数配置要求高的特点，因此，本文采用自适应白噪声的完整聚合经验模态分解（Compete Ensemble Empirical Mode Decompo‑sition with Adaptive Noise，CEEMDAN）算法强大的序列分解能力，减弱遥测序列的非线性、非稳定特性。在极限学习机（ELM）参数配置少、学习速度快、泛化性能好的基础上，利用粒子群优化（PSO）算法优化极限学习机的输入权值矩阵和隐含层偏差，减少ELM 算法随机性所造成的偏差。本文提出一种基于CEEMDAN-PSO-ELM 组合预测模型，以提高卫星遥测序列短时预测精度。

1 CEEMDAN 方法

EMD 是美国国家航空航天局（NASA）黄愕等在1998 年提出的信号分析方法［7］，该方法能把任意信号分解成若干固有模态分量（Intrinsic Mode Functions，IMF），克服了小波变换选取小波基和难以分解尺度的问题。每个IMF 需满足2 个条件：1）极值点个数与穿0 点个数相等或相差1 个；2）由所有极大值点形成包络和由所有极小值点形成包络均值为0。但是每个IMF 中可能会存在不同程度的模态混叠现象，对预测造成不利的影响。TORRES等［8］在HUANG 等的研究基础上提出了CEEM‑DAN 算法。该方法在每一次分解中都添加自适应的白噪声平滑脉冲干扰，可有效解决模态混叠现象，使数据分解更加完整。使用CEEMDAN 算法对卫星遥测数据进行分解，可实现该数据的平稳化，对后续的高精度、高适应度预测起到非常重要的作用。

CEEMDAN 算法分解的具体处理步骤如下：

步骤1对给定遥测数据x(n)上添加不同幅值的标准正态分布的白噪声wi(n)，γ为白噪声的幅度，第i次的数据序列为

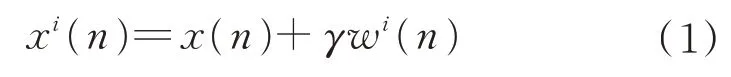
步骤2应用EMD 方法分解目标遥测数据，获取第1 个模态分量取均值：

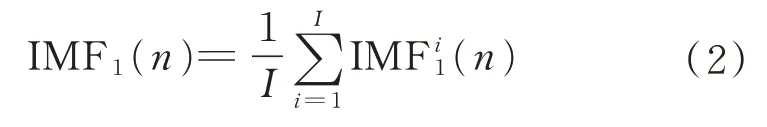
余量表示为

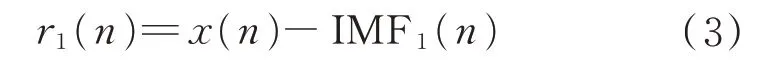
步骤3定义Ek(·)为遥测数据进行EMD 分解操作后的第k个IMF 分量，对序列r1(n)+γ1E1(wi(n))分解，得到这一部分的IMF 分量为

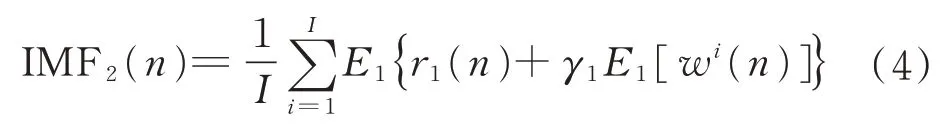
第2 个剩余分量为

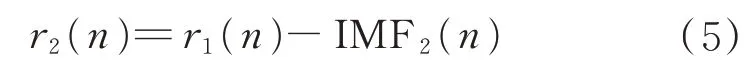
步骤4如此类推第k个剩余分量

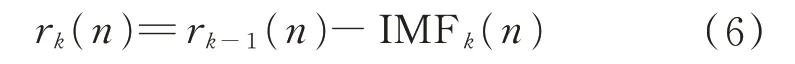
第k+1 个IMF 分量为

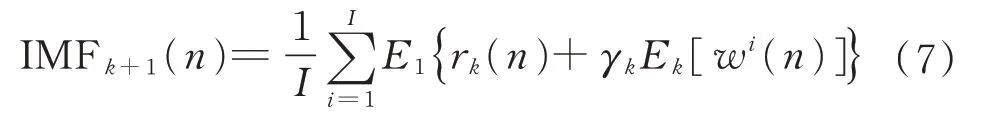
步骤5一直重复步骤4，直至剩余分量无法符合EMD 分解条件或迭代终止。最终，遥测数据被分解为

式中：R(n)为剩余分量。

2 粒子群优化ELM 算法

2.1 极限学习机相关概念

极限学习机（ELM）作为单隐层前馈神经网络，由黄广斌教授在2004 年提出［9］。作为一个单隐层前馈神经网络，输入权值和隐藏层偏差是随机产生的，输出权值是通过分析计算得到的。极限学习机的算法结构简单，学习速度快，并具有良好的全局搜索能力以及优秀的泛化性能。该算法随机产生输入层和输出层之间的权值和阈值，且在训练过程中无需调整，只要设置隐含层神经元个数，便可以获得预测误差最小的唯一解［10］。

ELM 预测算法的步骤如下：

步骤1输入。具有Q个样本的遥测训练集输入矩阵Xin和输出矩阵Xout，

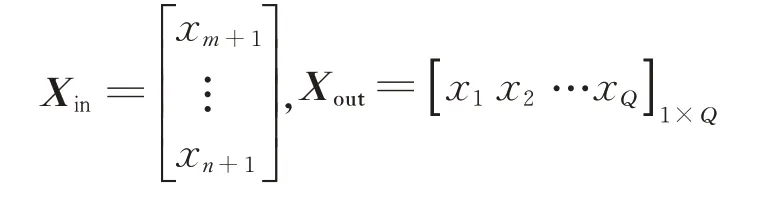
隐含层神经元的激活函数g(x)，本文用Log-Sigmoid 函数。

步骤2权值与阈值计算。随机生成输入层与隐含层的连接权重ω和隐含层神经元的阈值b。计算神经网络的隐含层输出矩阵H，具体形式为

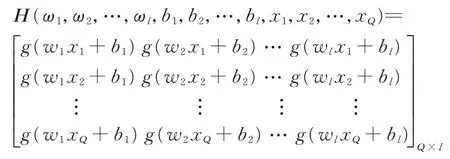
隐含层与输出层的连接权值为

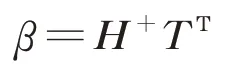
式中：H+为隐含层输出矩阵H的摩尔-彭罗斯广义逆矩阵；T=[t1，t2，…，tQ]m×Q，

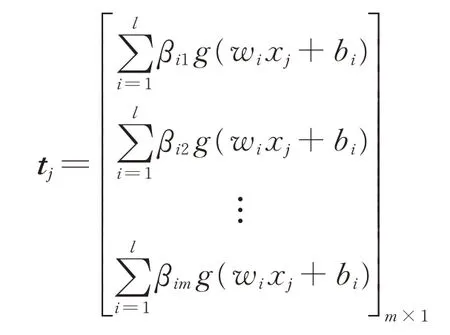
步骤3输出。根据测试样本集Y和输出权值β，计算出测试样本集的预测值。

2.2 粒子群优化极限学习机

由于ELM 初始输入权值和隐含层偏差是随机确定的，训练精度和时间都会受随机性影响，采用粒子群优化（Particle Swarm Optimization，PSO）算法对ELM 初始权值和阈值进行优化［11］。PSO 算法将搜索空间比作在群鸟觅食模型中，每个个体都可以看成一个粒子，鸟群可被看成一个粒子群。假设在一个目标搜索空间中，有m个粒子组成一个群体，第i个粒子位置表示为该粒子在D维空间的位置就是Xi。每个粒子的位置就是一个潜在解，将Xi代入目标函数可计算其适应度，根据适应度的大小衡量其优劣。粒子个体经历的最好位置为整个群体所有粒子经历的最好位置为粒子i的速度记为采用如下公式对粒子所在位置不断更新：

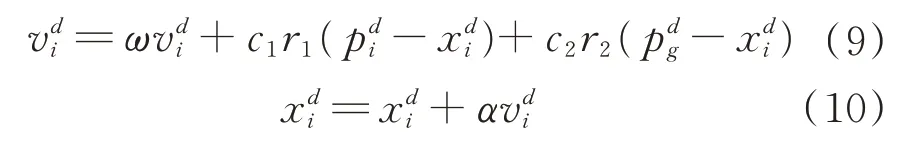
式中：i=1，2，···，m；d=1，2，···，D；ω为非负数，称为惯性因子；加速常数c1和c2为非负常数；r1和r2为［0，1］范围变换的随机数；α称为约束因子，用来控制速度。

PSO 优化ELM 预测模型的流程如图1 所示。

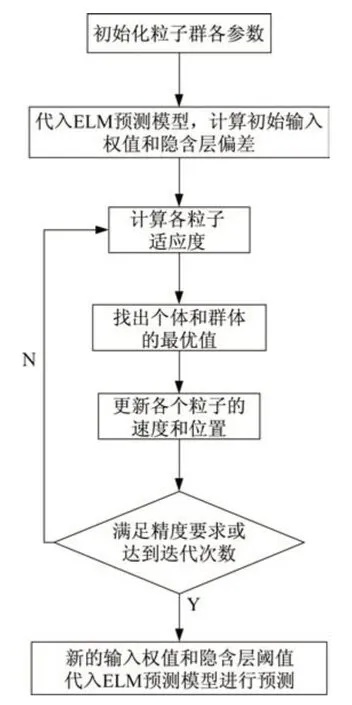
图1 PSO-ELM 优化流程Fig.1 PSO-ELM optimization process

3 CEEMDAN‑PSO‑ELM 预测模型搭建

3.1 遥测序列预处理

首先对遥测序列进行野值剔除，由于篇幅有限，本文不展开描述。通过对历史卫星遥测数据观察得知，卫星遥测序列连续帧数据是在小范围内波动变化，若直接利用，不仅造成数据过于冗余，还不利于预测。所以本文对遥测序列等时间间隔τ取均值，不仅可以压缩数据，而且能进一步减少残留野值的影响的作用。

对经过CEEMDAN 分解后的遥测序列{x1，x2，···，xn} 进行相空间转化，得到样本如下所示：

对上述矩阵求转置，选取一部分作为训练样本的输入输出，另一部分作为测试样本的输入输出。m为极限学习机输入层的神经元个数，隐含层神经元根据样本的个数来确定，输出为一个神经元，即进行单步预测。后续可以使用预测值替换测试集中陈旧数据，依次循环，以实现遥测序列的不断预测。

3.2 模型搭建

结合CEEMDAN 强大的数据分解能力与PSOELM 优秀的全局搜索能力，以及良好的泛化性能，本文提出CEEMDAN-PSO-ELM 预测模型［12-13］，并应用在卫星遥测数据预测中，流程如图2 所示。

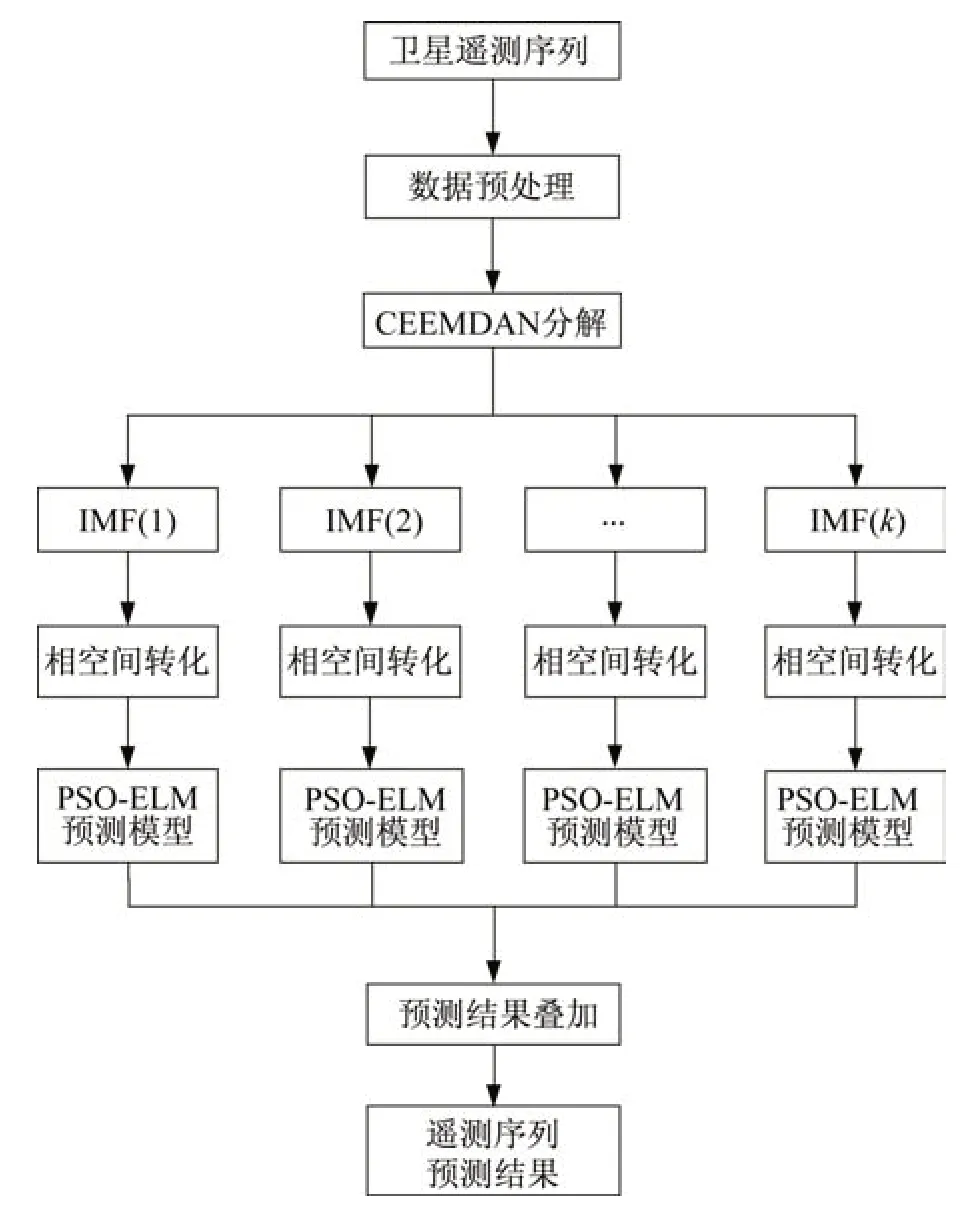
图2 CEEMDAN-PSO-ELM 预测流程Fig.2 CEEMDAN-PSO-ELM prediction process

使用CEEMDAN 把波动较强的卫星遥测序列，分解为相对平坦的序列组，利用经过PSO 算法优化的ELM 预测模型分别进行预测，最后叠加得到遥测序列的预测结果。

3.3 评价指标

通过以下指标评价预测模型的预测精度和拟合效果。

1) 平均绝对误差（MeanAbsoluteError，MAE）

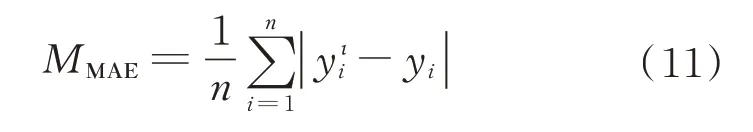
2) 平均绝对百分比误差（Mean Absolute Per‑centage Error，MAPE）

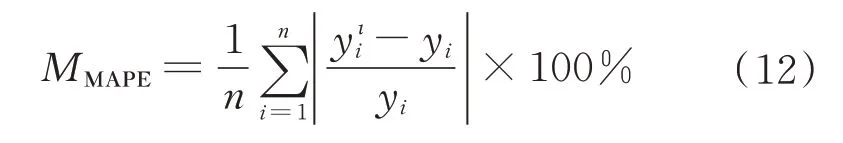
反映被测量数据整体的可信度。

3) 均方根误差（Root Mean Square Error，RMSE）

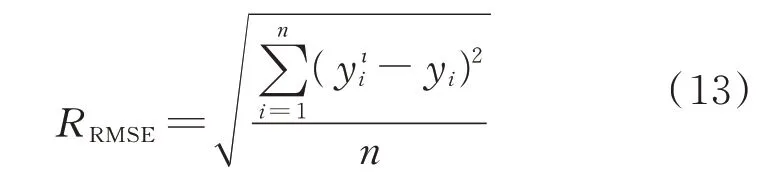
反映测量的精密度。

4) 标准均方误差（Normalized Mean Square Error，NMSE）

反映偏差和测量数据震荡强度关系。

4 基于CEEMDAN‑PSO‑ELM 的卫星遥测预测模型实验与分析

所有算法在Matlab R2014b 软件中编程实现。使用某高轨卫星的长光照期电池电压遥测数据和地影期间电池电压遥测数据进行预测精度对比实验。

4.1 电池电压预测结果与分析

为了验证本文算法对卫星遥测预测的有效性，比较神经网络预测算法中常使用的Elman 预测算法、ELM 预测算法及PSO-ELM 预测算法，并选用MAE、MAPE、RMSE、NMSE 指标评价算法性能。

4.1.1 长光照期预测结果与分析

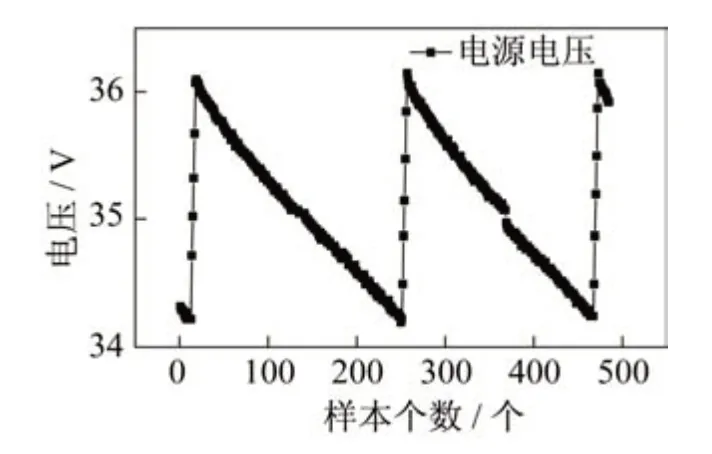
图3 长光照期电池电压遥测曲线Fig.3 Battery voltage telemetry curve during long-light period

该期间遥测数据的变化情况如图3 所示。由图可见，在此期间遥测变化规律性较强，预测难度不大。选择前365 个数据作为训练样本，后121 个数据作为测试样本。

利用CEEMDAN 算法对前365 个遥测进行分解，分解时添加500 组标准差为0.2 的白噪声信号，如图4 所示。由图可见，每个IMF 中基本上没有模态混叠现象。

采用滑动单步预测，滑动窗口设为6，预测结果比对如图5 所示，与其他预测模型相比，CEEM‑DAN-PSO-ELM 预测模型结果与真实值最接近，Elman 模型、ELM 模型和PSO-ELM 模型都在拐点处与真实值有不同程度的偏差，而CEEMDANPSO-ELM 预测模型在拐点处与真实值基本一致。

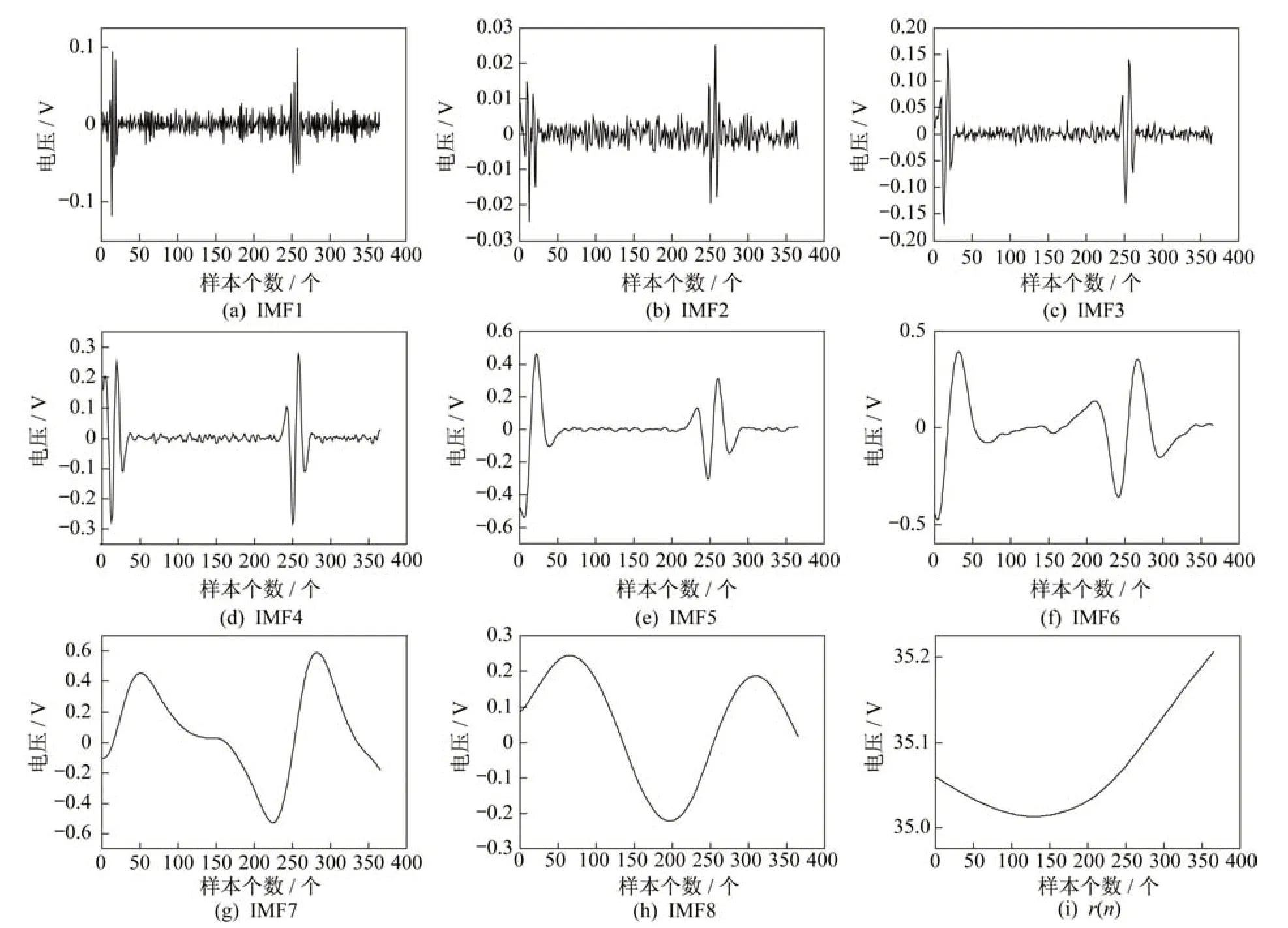
图4 长光照期电池电压CEEMDAN 分解图Fig.4 Battery voltage CEEMDAN decomposition diagram during long-light period

预测性能评价指标见表1，CEEMDAN-PSOELM 预测算法在MAE、MAPE、RMSE、NMSE 评价指标上都表现最好，PSO-ELM 预测算法次之，ELM 预测算法相对较差。

4.1.2 阴影期预测结果与分析

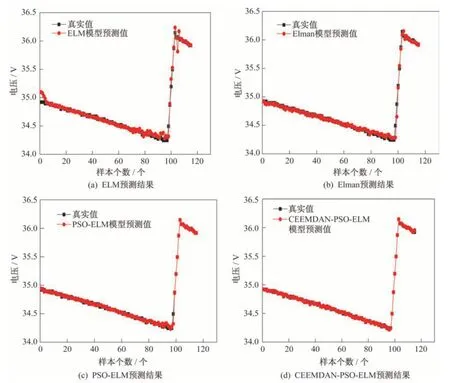
图5 长光照期电池电压预测结果比对Fig.5 Comparison of battery voltage prediction results during long-light period

该期间遥测数据的变化情况如图6 所示。由图可见，在此期间遥测周期变短，同时受地影期的时间长短影响，遥测曲线呈现出不规律的变化，难以预测。选择前479 个数据作为训练样本，后160 个数据作为测试样本。

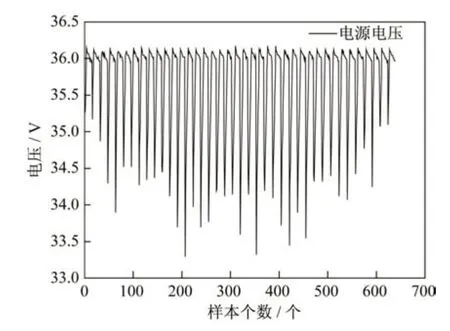
图6 地影期电池电压遥测曲线Fig.6 Battery voltage telemetry curve during ground shadow

利用CEEMDAN 算法对479 个数据进行分解，分解时添加500 组标准差为0.2 的白噪声信号，如图7 所示。由图可见，经过分解后每个IMF 都呈现出了规律性，此时预测相对容易。

采用滑动单步预测，滑动窗口设为6，预测结果如图8 所示。图8（a）和图8（b）中可以看出，ELM 预测法与实际值产生很大的偏差，Elman 预测法相对偏差较小，但也无法准确预测。图8（c）和图8（d）中可以看出，PSO-ELM 预测法相比ELM 预测法偏差小了很多，但依然在曲线最低点处有很大的偏差，而CEEMDAN-PSO-ELM 预测法基本与真实数据一致，达到很好的预测效果，而且设计人员最关心的是地影期间电池电压的放电深度等问题，所以精确地遥测预测对故障预测起到至关重要的作用。

预测性能评价指标见表1，CEEMDAN-PSOELM 预测算法在MAE、MAPE、RMSE、NMSE 评价指标上都表现最好，PSO-ELM 预测算法次之，ELM 预测算法相对较差。

图7 地影期电池电压CEEMDAN 分解图Fig.7 Battery voltage CEEMDAN decomposition diagram during ground shadow

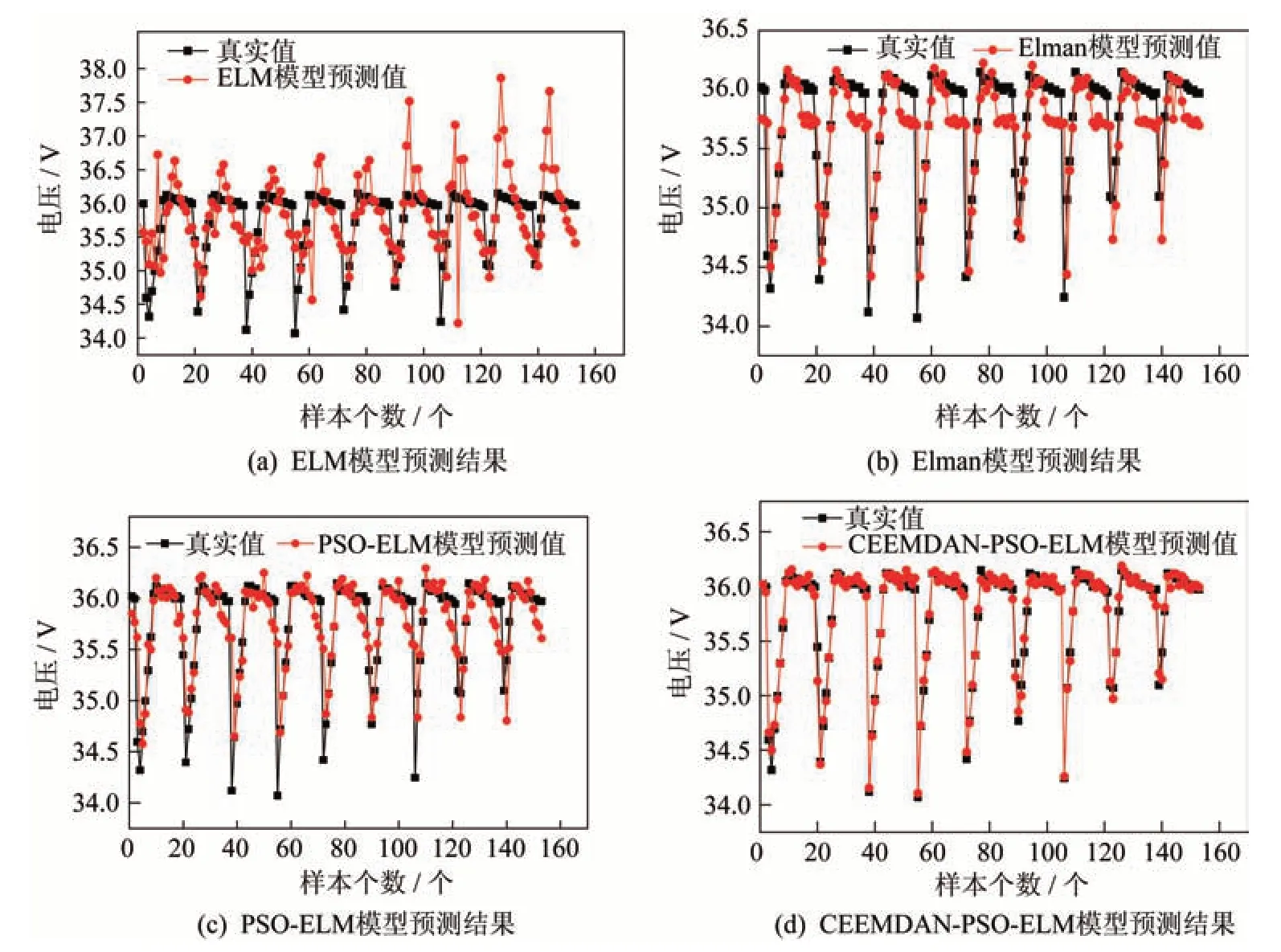
图8 预测结果比对Fig.8 Comparison of prediction results

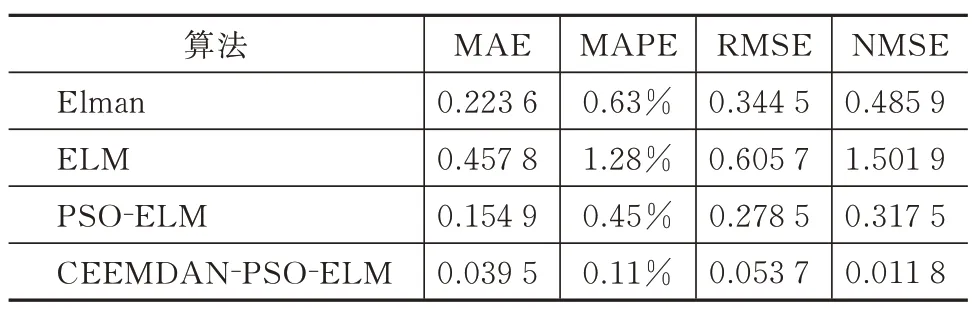
表1 预测性能对比Tab.1 Prediction performance comparison

5 结束语

本文基于在轨卫星历史遥测数据，提出了一种CEEMDAN-PSO-ELM 预测模型，利用某高轨卫星的长光照期间遥测数据和地影期间遥测数据进行模型验证比对实验。实验结论如下：1）与其他预测模型相比，该方法与真实值最为接近，在平均绝对百分比误差、均方根误差、标准均方误差等指标上均最小。2）与其他预测模型相比，该方法在拐点处预测优势明显，且该算法对遥测变化规律性要求不高，可扩展至其他遥测变化类型预测中。如何选用合适的遥测参数进行预测，并结合一些异常检测的方法从预测的结果中发现异常，实现故障预测是今后的课题。同时，如何实现卫星遥测数据在线预测也是未来重要的研究方向。