基于改进灰色模型的遥测变量预测方法

李 楠，陈重华，陈国忠，黄 欣，陆启省

（上海卫星工程研究所，上海 200240）

0 引言

伴随着空间技术的发展，对航天任务的需求也日益复杂化。相应地，卫星在轨工作时间以及自身结构的复杂性也大幅增加，这就使得如何保障其在轨运行期间的工况稳定度，如何提高其在轨运行期间的自主维护能力，成为当今航天领域的一大难题。在此背景下，基于各种算法的遥测变量预报技术作为解决上述问题的有效手段一直以来备受业界关注。

在众多算法中，灰色预测模型作为将系统论、信息论及控制论观点延伸到抽象系统而发展出的一套专门用于解决贫数据、信息不完备问题的新方法，在生产制造中，尤其是航空航天领域应用广泛［1-4］。但是，在实际操作中发现，此模型的预测效果有时理想，有时偏差较大，甚至完全失效［5-7］。究其原因，灰色预测模型从本质上可以认为是指数预测模型，其预测精度与被预测对象递变规律以及数据序列的光滑程度有关。目前对此已提出的典型改进方法有：数据预处理方法［8］、初始条件改进方法［9-12］、背景值改进方法［13-14］等。这些方法虽然在一定程度提高了模型拟合精度，但预测效果仍不够理想，并且它们多是以灰色模型为基础附加了额外算法，考虑到附加算法的复杂性，往往使得预测过程计算量大大增加。

鉴于此，文章结合经典灰色理论及GM（1，1）建模方法分析，就遥测数据整定，提出一种改进的处理算法，使变换后遥测数据更加光滑，符合GM（1，1）建模要求，对于提高在轨航天器未来状态预测的准确度意义重大。

1 改进算法的提出

1.1 光滑比的概念

小样本、贫信息、不确定性系统的大量存在，决定了GM（1，1）模型具有十分宽广的应用领域。但是GM（1，1）模型也有一定的适用范围，超出该范围，应用GM（1，1）模型较难取得理想的预测结果。

注意到GM（1，1）模型本源上属于一阶微分方程，故而其更适用于描述初始数据序列发展趋势呈单调变化的情况。经多次试验、计算发现［8］：无论原始数据序列呈现递增或递减态势、数据曲线形状呈凹或凸状，由GM（1，1）模型响应函数式与系统还原公式计算得到的最终结果皆呈凹形曲线。在此情况下，GM（1，1）模型使用将受到一定限制。究其原因，GM（1，1）模型的预测精度受到原始数据递变规律的密切影响，考虑到灰色模型的解具有指数函数形式，所以对于已经生成指数变化趋势的建模数据，关系GM（1，1）模型精度的真正原因是由于初始数据序列x(0)不满足光滑离散函数的条件。

处处可导是光滑连续函数的特性，而序列是由离散的单个点构成的，根本无导数可言（通常意义下），因此，不能用导数研究序列的光滑性。从另外的角度研究光滑连续函数的特性，若某序列具有与光滑连续函数大致相近的特征，便认为此序列是光滑的。

设非负初始数据序列

z为x(0)的均值生成序列，即

x*为某一可导函数的代表序列，将x(0)删去x(0)(n+1)后得到的序列记为x′，若x′满足：

则称x′为光滑序列。上述两条件称为序列光滑条件。

实际中，应用灰色系统理论建模时，并不要求初始数据序列严格满足光滑条件，对于在一定程度上满足光滑条件的数据，建立相应的GM（1，1）模型也能取得满足工程实际要求的精度。

为了定量描述数据序列的光滑性，引入光滑比的概念，即

光滑比从另一侧面反映了序列的光滑性，即用序列第k个数据x(0)(k)与其前k-1 个数据之和的比值ρ(k)，来考察序列x(0)中数据变化是否平稳。显然，序列越平滑，其光滑比越小，若序列x(0)满足：

2）ρ(k)∈[0，ε]，k=3，4，…，n；

3）ε＜0.5。

称该序列为准光滑序列。

1.2 综合变换函数构造

初始数据序列作累加处理后呈现明显的指数规律［9］，是灰色系统理论建模基础。然而，杂乱无章的数据序列经累加生成所建立的GM（1，1）模型，往往会产生较大偏差的预测结果。就此，国内外诸多学者对模型的应用条件展开了深入长期的研究：文献［15］提出建立GM（1，1）模型的条件是初始离散数据序列为光滑离散函数；文献［6-8］分别结合实例分析，进一步说明光滑离散函数性质对建模的重要性。可见，提高初始数据序列光滑度是十分必要的，本文以光滑比概念为基础，提出一种改进序列光滑度的综合变换函数。

首先借助1.1 节中提出的序列光滑比的概念，给出描述光滑离散函数的主要条件如下［15］：

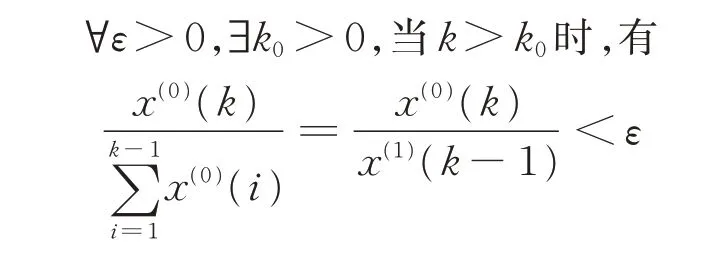
接下来，以命题形式提出如下序列光滑度改进算法：设{xi}，i=1，2，…，n为严格单调递增非负序列，有

式中：参数0 ＜α＜1；γ＞0；β·xi+γ≥e(2.718 3)。

1.3 变换有效性证明

将上述算法拆分为4 个命题进行证明，即

命题1设{xi}，i=1，2，…，n为严格单调递增非负序列，则对于∀γ＞0，有如下结论成立：

证明记f(x)=β·x+γ，γ＞0，由

命题1 得证，且该命题说明线性变换可以提高序列光滑度。

命题2设{xi}，i=1，2，…，n为严格单调递增非负序列，且x1≥e(2.718 3)，则有如下结论成立：

证明记f(x)=lnx，对于x≥e(2.718 3)，由

命题2 得证，且该命题说明对数变换可以提高序列光滑度。

命题3设{xi}，i=1，2，…，n为严格单调递增非负序列，则∀0 ＜a＜1，有如下结论成立：

证明 记f(x)=xα，0 ＜α＜1，由

命题3 得证，且该命题说明幂指变换可以提高序列光滑度。

命题4即文章提出的数据序列平滑算法，见式（2）。

证明考虑到{xi}为严格单调递增非负数据序列，则∀β，γ≥0 且β·γ≠0，有{β·xi+γ}仍为严格单调递增非负序列。

且{ln(β·xi+γ)} 也为严格单调递增非负序列。

再由命题3 易知，∀0 ＜a＜1，有

综合上述结论，有

命题4 得证。

显然，通过上述证明可见：线性变化得到的数据序列较原始序列光滑程度有所改善，在此基础上继续施加对数变换将使更新序列的光滑程度进一步得到提升，而最终复合的幂指数变换将得到较单纯线性变换、对数变换，或线性变换与对数变换组合变换光滑程度更优的结果。此外，文章提出的这种改进算法由于包含可调参数（α，β，γ），增加了应用灵活性和适应性，即通过参数调整，实现人机对话，使GM（1，1）模型的拟合及预测效果更加符合客观实际需要。

2 遥测数据仿真验证

为进一步验证文章改进方法的有效性，以FY卫星SADA（南）轴承温度信号（TK-25）6—9 月的15 和30 日平均值为例进行分析，具体数据见表1。

表1 FY 卫星SADA（南）轴承温度信号6-9 月的15 与30 日均温度Tab.1 Bearing’s daily（15th and 30th）average temperature of the FY satellite SADA（south）from June to September

由于序列各项数值皆小于零，故先对其进行如下变换：

式中：int 为向上取整函数（靠近abs(xi)且取值较大的数值）。

变换后，得到的新序列为

显然，该序列非负且单调递增。对其进行1-AGO，得到

对序列光滑性进行验证，即：

应用文章改进算法，首先对序列{x(0)} 依照式（2）进行变换，变换参数依次取为α=0.9，β=11，γ=0，则计算得到新序列

显然，算得序列单调递减，故变换后{y(0)}为离散光滑的，满足GM（1，1）模型建模条件。

按照一般步骤建立{y(0)}的GM（1，1）模型，有

由轨航天器状态预测统计结果（见表2）易见：采用文献［15］所述传统方法建立的GM（1，1）预测模型误差巨大，其中采样数据的拟合相对误差最大达到664.085 6%，平均相对误差也高达125.022 9%；采样数据外的两步预测结果更是面目全非，平均相对误差更是升至惊人的2 278.805 2%，由此得出该预测模型无效。结合灰色系统理论不难发现，采样数据不符合GM（1，1）建模要求，即{x(0)}不满足光滑离散函数条件是造成这种状况的根本原因。对此，文章改进算法通过对初始数据序列依式（2）进行变换，改善其光滑度，提高建模精度，其中拟合平均相对误差以及两步预测平均相对误差较先前方法分别降至3.998 8% 和24.605 4%，预测模型有效。

表2 FY 卫星SADA（南）轴承温度信号灰色模型拟合及预测结果Tab.2 Fitting and prediction results of the bearing’s temperature data of FY satellite SADA（south）by using different GM algorithms

3 结束语

针对现有灰色系统预测方法所存在的建模精度、外推能力依赖于生成序列光滑程度的问题，提出一种能够显著提高模型预测精度的改进算法。本文分别通过严格的理论证明和仿真分析发现，该方法通过构造复合函数，不但使得变换后的建模数据较采用传统幂函数平滑方法、线性函数平滑方法以及对数函数平滑方法具有更好的光滑程度，而且通过引入可调参数使得算法具有更大灵活性和更广的适用范围。