复合材料壳体固体火箭发动机温度载荷下力学响应分析

王 倩，王佳兴，隋 欣，张亚俊，王宁飞

（1.北京理工大学 宇航学院，北京 100081；2.上海航天动力技术研究所，上海 201109；3.西安近代化学研究所，陕西 西安 710065）

0 引言

壳体作为固体火箭发动机的重要组成部分，在工作过程中承受高温、高压的作用。复合材料具有强度高、质轻的优点，符合发动机壳体设计的需求，在保证发动机壳体的力学性能的同时，可以有效降低固体火箭发动机的消极质量［1］。近年来，随着复合材料在固体火箭发动机壳体上的广泛使用，研究复合材料壳体的固体火箭发动机结构完整性问题也愈加重要。

对于传统的金属壳体发动机，其固化降温过程中的结构完整性问题已经得到比较充分的研究［2-3］。徐新琦等［4］对一种贴壁浇铸星型固体火箭发动机在固化降温过程中的三维瞬态温度场进行了数值模拟，并基于药柱的黏弹性本构关系计算了由瞬态温度场引起的应力应变响应。邓康清等［5］通过热-机耦合对于自由装填式的固体火箭发动机在低温点火下的结构完整性进行了分析。刘中兵等［6］研究了管型药在低温和点火升压两种载荷下的结构完整性。隋欣等［7］对大过载作用下发动机装药的强度进行了数值仿真，并分析装药结构对于应力应变场的影响。

然而复合材料壳体的材料性能与金属壳体相差较大，在各种载荷作用下的受力变形也不同于金属壳体。因此，传统的金属壳体固体火箭发动机的结构完整性的研究结果，并不能够准确描述复合材料壳体固体火箭发动机的结构完整性。现有的针对复合材料壳体固体发动机的研究，主要集中在各种载荷作用下的复合材料壳体的受力分析以及针对复合材料壳体本身的结构设计，包括复合材料壳体在温度、内压作用下的有限元分析，复合材料壳体的纤维缠绕方式、铺层方案等。戴进等［8］将纤维缠绕固体发动机在内压作用下的变形作为轴对称大变形问题，采用全拉格朗日法对纤维缠绕固体发动机进行有限元分析，并在此基础上完成了纤维缠绕复合材料壳体大变形有限元软件的编制。梁群等［9］建立了壳体固化成型过程的热-化学耦合数学模型，数值模拟了固体火箭发动机壳体在固化降温过程中的温度变化历程。张治纲［10］对YY-1 固体火箭发动机的纤维缠绕复合材料壳体进行仿真计算，研究了该壳体在内压载荷和轴压载荷条件下的有限元破坏机理。程昕等［11-12］分别在自己的研究中运用有限元软件对复合材料壳体进行仿真计算，对纤维缠绕固体火箭发动机壳体的纤维铺层方案进行了求解。

可见，上述研究主要关注复合材料壳体本身，对于复合材料壳体与装药整体的分析则较为少见。本文旨在研究在固化降温过程中，复合材料壳体固体火箭发动机整体力学分析，重点研究装药和壳体的应力、应变场分布，分析在固化降温过程中壳体与装药耦合情况下的受力及变形。

本文采用有限元数值仿真分析方法，使用有限元计算软件ABAQUS 分别建立金属壳体与复合材料壳体两组发动机计算模型；在相同载荷下，对比金属材料壳体与复合材料壳体的发动机的仿真模拟结果，分析出复合材料壳体的固体火箭发动机相对于传统金属壳体的发动机在结构完整性方面的特点；同时研究复合材料壳体的厚度、弹性模量以及泊松比对于发动机装药和壳体的应力场的影响。

1 试验模型与有限元仿真模型

1.1 准确性验证模型

试验模型为复合材料壳体的端燃装药固体火箭发动机，模型结构如图1 所示。

图1 试验模型Fig.1 Test model

试验条件为环境温度由58 ℃降温至20 ℃，测量药柱在距离前封头赤道线190 mm、390 mm、590 mm、790 mm、990 mm 处0°、90°、180°、270°的收缩量，试验测量结果见表1。

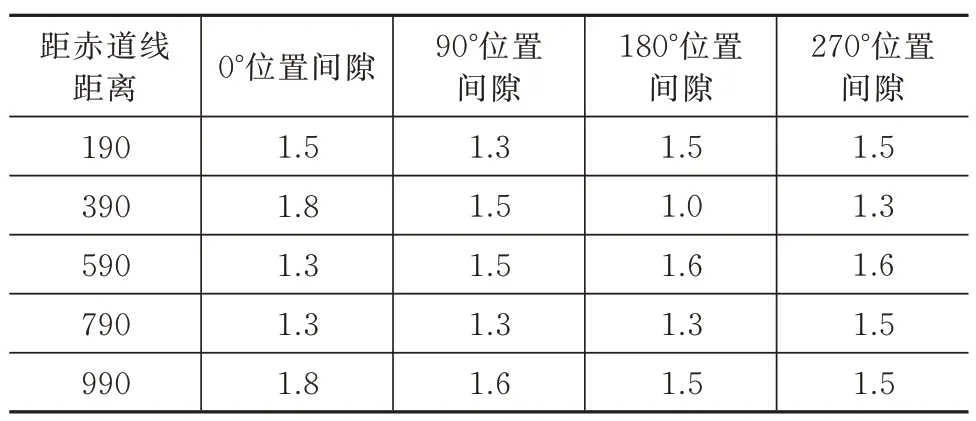
表1 降温至20 ℃时装药半径收缩量试验测量值Tab.1 The measured value of grain shrinkage test when the temperature decreases to 20 ℃ mm

根据试验模型，建立仿真验证有限元模型，如图2（b）所示；并建立与之相对照的金属壳体发动机模型，如图2（a）所示。

金属壳体与复合材料壳体发动机装药结构尺寸完全相同，装药半径最大处为243.3 mm，长度为1 169.5 mm，复合材料壳体厚度在圆筒段为4 mm，与金属壳体一致，前后封头处稍作加厚处理，其他部件只在前、后接头部位稍做调整。考虑到载荷和模型的对称性，取1/8 进行建模和计算。网格类型为四结点线性四面体单元C3D4，金属壳体发动机的网格数量为31 116，复合材料壳体发动机的网格数量为49 915，相邻界面网格加密并合并节点。

图2 发动机有限元模型Fig.2 Finite element model of SRM

1.2 计算假设

为便于计算，假设推进剂各向同性、均匀，为线性黏弹性材料；推进剂泊松比为常量，不随时间和温度变化；绝热层的热力学参数为常量，不随时间和温度变化；装药变形较小，属于小变形理论范畴；对于复合材料壳体，将其作为各向异性材料，只考虑其宏观的力学性能，忽略微观特性。

1.3 材料参数

装药采用复合推进剂，其松弛模量表达式为

式中：E（t）为松弛模量；t为时间。

Williams-Landel-Ferry 方程为

式中：αT为位移因子；T为参考温度，设为293.15 K。

其他材料参数见表2 和表3[13-14]。表3 中，E为杨氏模量，μ为泊松比，G为剪切模量。

1.4 边界条件与载荷

设置对称面上为对称约束，限制发动机壳体前顶盖位置表面上节点的轴向位移，以初始温度58 ℃为零应力温度，设置两组工况。

工况1：环境温度为20 ℃，在壳体外表面施加20 ℃温度载荷。

表2 推进剂、绝热层、前后接头及金属壳体与复合材料壳体的物性参数Tab.2 Physical parameters of propellant，insulation layer，fwd/aft polar-bosses，metal cases and composite cases

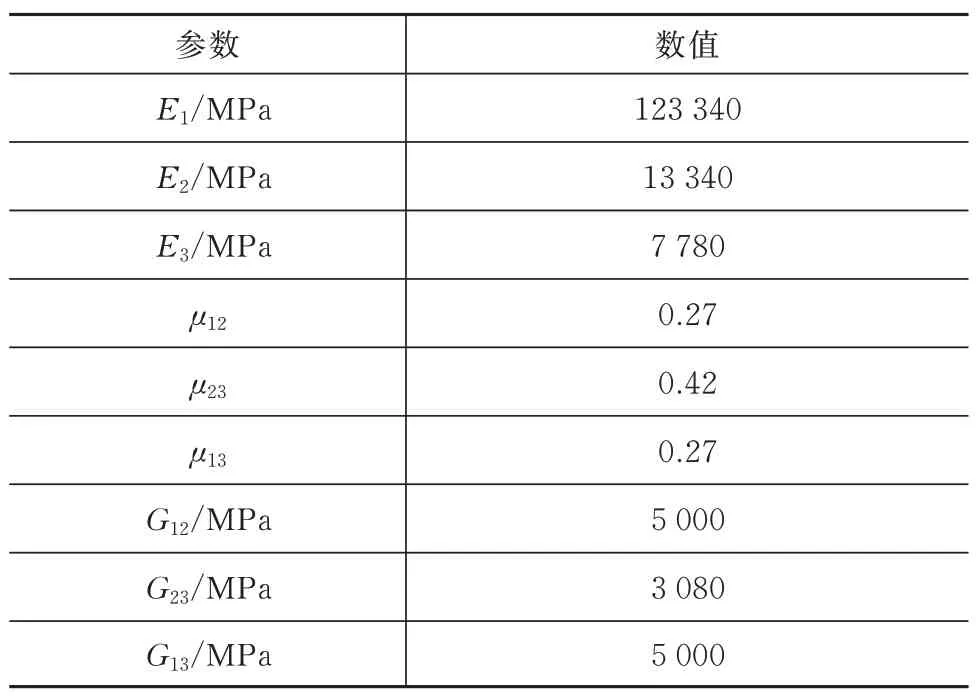
表3 复合材料壳体的力学参数Tab.3 Mechanical parameters of the composite case

工况2：环境温度为-40 ℃，在壳体外表面施加-40 ℃温度载荷。

直到发动机内外温度均匀，与环境温度达到一致，降温时长为4 d。

2 有限元分析结果

2.1 准确性验证

对于工况1，当降温至20 ℃时，复合材料壳体发动机的装药半径在试验模型测量点处变形量分别为1.43 mm、1.42 mm、1.40 mm、1.40 mm、1.39 mm。

由于试验模型在0°和180°的变形量除温度载荷外，受到重力因素影响，所以取90°和270°的试验测量结果的平均值与仿真计算结果对比，如图3 所示。由图可见，在误差允许的范围内，试验结果与仿真结果较为符合，仿真研究方法具有准确性。

图3 装药半径收缩量试验结果与仿真结果对比Fig.3 Comparison of test results and simulation results of grain shrinkage

2.2 装药变形分析

对于工况2，当降温至-40 ℃时，金属壳体与复合材料壳体的发动机整体变形如图4 所示。

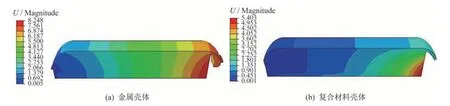
图4 两种发动机位移云图Fig.4 Displacement contour map of two SRMs

固化降温后，装药整体缩短，装药端面变形量最大。对比两种壳体的变形云图，复合材料壳体的发动机装药的径向变形相对均匀，壳体变形与装药变形也趋于一致，两者都整体缩短约8 mm；金属壳体的发动机壳体变形较小，约缩短1.5 mm，靠近壳体的装药变形较小，而在中心线上变形较大，中心线处的装药缩短了约5 mm。

2.3 装药应力应变分析

金属壳体与复合材料壳体的发动机整体应力场分布云图如图5 所示，金属壳体与复合材料壳体发动机装药的应力应变场云图如图6 和图7 所示。

图5 两种发动机整体Von Mises 等效应力云图Fig.5 Von Mises contour map of two SRMs

图6 两种发动机装药Von Mises 应力云图Fig.6 Von Mises contour map of two SRM grains

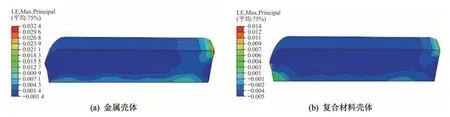
图7 两种发动机装药应变云图Fig.7 Logarithmic strain contour map of two SRM grains

以装药轴线上的节点从装药头部到端面作路径1，以装药端面上的节点由圆心开始沿半径作路径2，如图8 所示。

图8 路径1 与路径2Fig.8 Path 1 and path 2

在路径1 上做Von Mises 等效应力-轴向距离、应变-轴向距离图，在路径2 上做Von Mises 等效应力-径向距离、应变-径向距离图，如图9 与图10所示。

图9 应力应变随轴向距离的变化关系Fig.9 Stress and strain at different axial distance

图10 应力应变随径向距离的变化关系Fig.10 Stress and strain at different radial distance

结合图5～图10 可以看出：

1）金属壳体发动机装药的Von Mises 等效应力、应变均大于复合材料壳体发动机装药的Von Mises 等效应力、应变。

2）金属壳体发动机装药的危险点出现在装药端面外缘，Von Mises等效应力最大值达到0.53 MPa，应变为3.24%。

3）复合材料壳体发动机，装药中心线上Von Mises 等效应力、应变从装药头部沿轴向向装药端面逐渐减小，而在靠近壳体部分Von Mises 等效应力、应变从装药头部沿轴向向装药端面逐渐增大。装药的危险点出现在两个部位，一是装药头部的中心线上，二是装药端面最外缘。其中，装药外缘的Von Mises 等效应力最大，为0.23 MPa，应变为0.93%。

在温度载荷下，复合材料壳体和金属壳体的固体发动机装药与壳体的受力变形结果见表4。

表4 发动机装药与壳体的应力、应变、位移结果Tab.4 Stress，strain and displacement results of grain and case

在固化降温过程中，复合材料壳体与装药和绝热层的热膨胀系数差别不大，使得发动机整体呈现出较为均匀的变形，在层间受力下也与装药呈现出较好的形变耦合。

而金属壳体的固体火箭发动机在固化降温过程中，由于壳体与装药和绝热层的热膨胀系数差别较大，在温度载荷下，产生了不同程度的收缩变形，装药的收缩变形趋势远大于壳体的变形趋势；而金属壳体的弹性模量较大，导致了装药在中心线上变形较大，在靠近壳体的部分变形较小。另一方面，相对于非金属壳体的固体发动机，由于金属壳体更多地限制了装药的形变，使装药得不到有效的应力释放，所以表现出壳体和装药的危险点上更大的应力、应变。

2.4 复合材料壳体发动机的装药应力、应变响应

根据壳体、绝热层和装药3 种材料的热膨胀系数，得知在温度载荷下，绝热层的变形程度最大；其次是装药，壳体的变形程度最小。不同材料的变形程度不同，导致了固化降温过程中装药与绝热层的黏接界面边缘受到拉应力，即装药端面外缘，此处为发动机装药的危险点。本文考虑复合材料壳体厚度、弹性模量和泊松比对于发动机装药的应力、应变场的影响。

2.4.1 复合材料壳体厚度对于装药应力应变场的影响

分别建立壳体厚度（设为δ）为3 mm、4 mm、5 mm、6 mm、7 mm 的5 个复合材料壳体的发动机模型，分别计算其固化降温过程的应力场分布，以此来分析装药的应力、应变随复合材料壳体厚度的变化关系。装药与壳体的应力云图如图11 所示。

图11 装药与壳体的Von Mises 等效应力云图Fig.11 Von Mises contour map of grain and case

对于不同厚度的壳体，发动机的应力应变场变化规律分布一致，装药的危险点始终在装药端面外缘，壳体的危险点位于壳体顶部与绝热层和前接头连接的位置。

当壳体厚度增量Δδ=1 mm 时，壳体厚度变化量相对于壳体厚度本身较大，对于装药的应力、应变的影响较为显著，并且体现为宏观上的影响。随着壳体厚度的增加，壳体对于装药和绝热层的变形约束增强，使装药在与绝热层黏接界面受到更大的拉应力和应变。同时壳体受到的应力减小，应力、应变随壳体厚度变化关系如图12 所示。

2.4.2 复合材料壳体弹性模量对于装药应力应变场的影响

分别设置复合材料壳体的环向和纵向弹性模量为120 GPa、130 GPa、140 GPa 和150 GPa，横向的弹性模量保持为7.78 GPa，分别计算其固化降温过程的应力应变场分布，以此来分析复合材料壳体的弹性模量对于装药的应力、应变的影响。

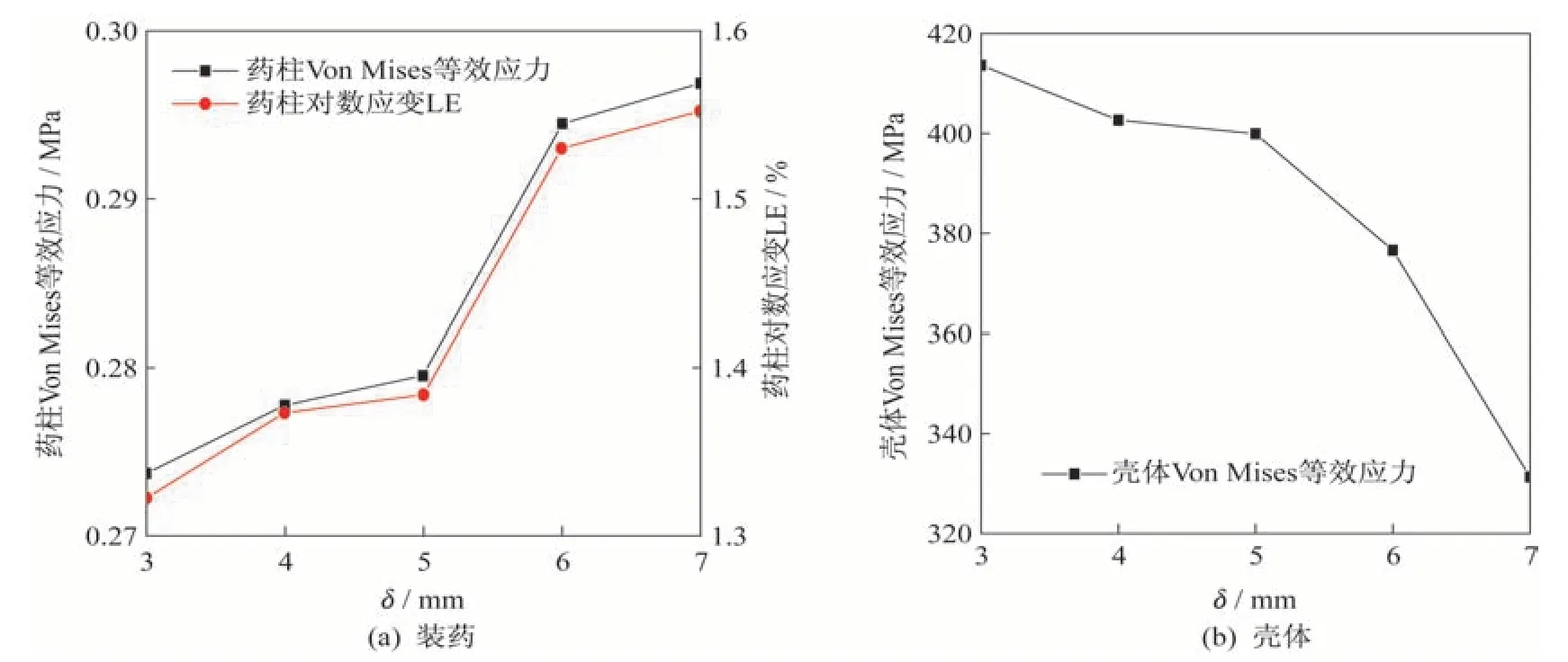
图12 应力应变最大值随壳体厚度变化关系Fig.12 Maximum stress and strain at different case thickness

装药和壳体危险点的应力、应变最大值随壳体的环向和纵向弹性模量的变化关系如图13 所示。由图可以看出，随着复合材料壳体纵向和环向的弹性模量增大，装药的Von Mises 等效应力、对数应变逐渐减小，但变化幅度都较小，而壳体的Von Mises等效应力和对数应变都不断增大。这是因为绝热层的热膨胀系数大于壳体与装药的热膨胀系数，而后两者热膨胀系数相差不大，降温开始后，绝热层的收缩速度大于装药与壳体；而随着壳体的弹性模量的增加，壳体对于绝热层变形的抵抗能力增强，但增强的程度尚不足以限制装药的变形。导致壳体所承受的应力、应变增大，而装药受到的来自于绝热层黏接界面的拉应力、应变都减小。

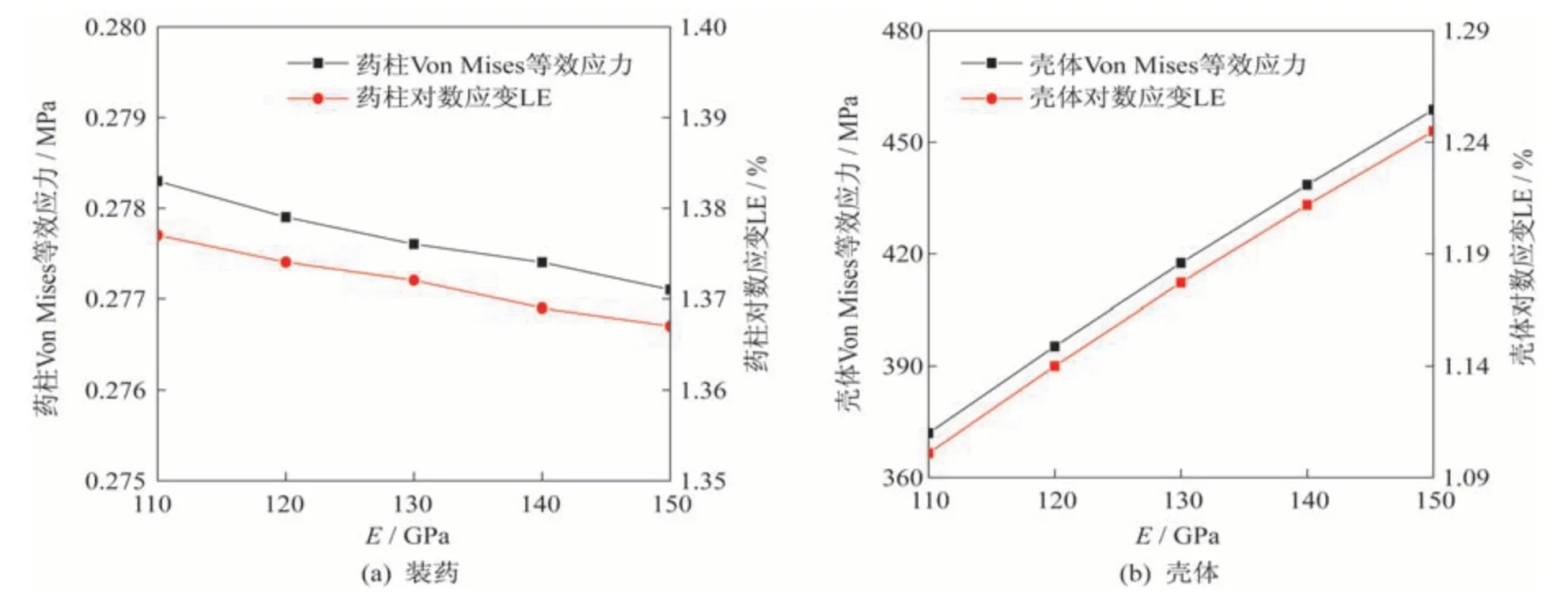
图13 Von Mises 等效应力、应变最大值随壳体弹性模量变化关系Fig.13 Maximum stress and strain at different elastic modulus

2.4.3 复合材料壳体泊松比对于装药应力应变场的影响

分别设置复合材料壳体的环向和纵向泊松比为0.26、0.28、0.30 和0.32，厚度方向的泊松比保持为0.42。分别计算其固化降温过程的应力场分布，以此来分析装药与壳体的应力、应变对于复合材料壳体的泊松比的响应。装药和壳体危险点的应力及位移最大值随壳体厚度变化的折线图如图14所示。

在壳体与绝热层和装药的变形耦合中，随着泊松比增大，壳体的剪切模量减小，且泊松比的变化量较小，所以在该情况下增大泊松比与减小壳体的弹性模量造成的影响效果相似。

如图14 所示，复合材料壳体的环向和纵向泊松比在0.26～0.32 范围内时，随着泊松比增大，装药的Von Mises 等效应力和对数应变逐渐增大，而壳体的Von Mises 等效应力和对数应变逐渐减小，且变化幅度都很小。

图14 Von Mises 等效应力、应变最大值随壳体泊松比变化关系Fig.14 Maximum stress and strain at different Poisson's ratio

3 结束语

在端燃装药固体发动机固化降温的过程中，采用复合材料壳体的发动机结构完整性优于金属壳体发动机。壳体的参数对于发动机装药的应力、应变均有一定的影响。随着复合材料壳体厚度增加，装药的应力、应变值均增大，壳体的应力逐渐减小；随着复合材料壳体纵向和环向的弹性模量增大或泊松比减小，装药的应力、应变逐渐减小，壳体的应力、应变逐渐增大。在未来的研究中，随着复合材料工艺的不断发展，复合材料壳体的固体火箭发动机的轻质化可以不断提升［15］，应用新型壳体材料的发动机的结构完整性与低易损性需要进行更加深入的研究。