电大尺寸天线罩电磁特性高效数值仿真技术

于冰洋，阙肖峰，聂在平

（电子科技大学电子科学与工程学院，四川成都 611731）

0 引言

天线罩是用于保护天线免受外部环境影响的一类设备，在雷达系统中应用广泛。随着电子技术的发展，天线罩作为雷达天线的电磁窗口，其电性能显得尤为重要，已经成为雷达天线的一部分［1］。在天线罩的设计过程中，准确、高效的电磁建模与仿真手段发挥着重要作用。目前，对天线罩的仿真计算方法主要有高频近似法和全波数值法两类［2-6］。高频法包括了物理光学法（PO）、弹跳射线法（SBR）等，其物理概念清晰，计算速度快。但是由于高频法是基于局部场近似原理，没有考虑天线罩各部分之间的电磁耦合关系，以及难以准确分析非平滑结构和复杂介质问题，在实际应用中会带来较大的误差。全波数值法包括了广泛采用的矩量法（MoM）、有限元法（FEM）和时域有限差分法（FDTD）等，这些方法考虑了全局电磁耦合关系，计算精度高，但是计算复杂度高且计算效率低，很长时间以来只能用于小尺寸天线罩的分析。为了在确保计算精度的前提下提高计算效率和计算能力，必须采用正确的电磁理论模型和高效的计算方法。

本文首先采用基于表面积分方程（SIE）的并行多层快速多极子算法（MLFMA），对电大尺寸天线罩的电磁特性进行仿真。相较于基于介质体模型和体网格剖分的数值算法［7］，SIE 仅需要在不同媒质的分界面上离散网格和构造基函数，极大地减少了数值计算量。然后提出了改进迭代求解效率的JMCFIE 表面积分方程和稀疏近似逆（SAI）预条件技术，并引入快速球谐展开（SE）技术，减少内存需求。数值算例验证了本文提出方法的正确性，以及在计算效率和计算资源需求方面的较大优势。最后，对大型阵列天线-天线罩辐射问题开展了一体化建模仿真，在单台小型服务器上完成上百电磁波长尺度天线罩问题的快速计算。

1 基本理论

1.1 天线罩问题的表面积分方程

天线罩电特性仿真实质上是求解导体-介质复合结构的电磁问题。导体和任意介质结构组合示意图如图1 所示。其中，导体包括闭合导体（如实体器件）和开放导体（如天线、频选等）结构。图中Di，…，Dq表示不同媒质区域，D0表示背景媒质区域，Sj表示Dj的表面，Sjl表示Dj和Dl分界面。阴影区Dq，Dp表示闭合导体区域，Dl表示开放导体区域。

根据等效原理建立开放导体表面的电场积分方程（EFIE）、闭合导体表面的混合场积分方程（CFIE），以及各介质区域内表面的EFIE 和MFIE。为改进矩阵方程性态，将介质表面的EFIE 和MFIE构造为JMCFIE：首先建立介质表面两侧的电流混合场积分方程（JCFIE）

和磁流混合场积分方程（MCFIE）［8］

式中：α和β为比例因子，α=0～1，β=1－α；下标j为第j个媒质空间。

将两侧的方程组合得到该分界面的JMCFIE。当α=1 时，则退化为广泛采用的PMCHW 方程。

通过以上处理，可以建立含罩天线系统电特性分析时的EFIE-CFIE-JMCFIE 矩阵方程形式。通过适当选择比例因子，利用伽略金方法得到矩阵方程为

由于阻抗矩阵具有良好的条件数，方程迭代求解效率高。

为实现电大尺寸天线罩的快速求解，本文采用了并行MLFMA 对矩阵方程加速计算［9］。MLFMA利用几何分组，将子散射体（基函数）之间耦合关系分为近区和远区关系。近区组内子散射体的耦合通过严格的MoM 直接计算；远区组内的子散射体耦合关系则利用加法定理将格林函数在谱域内进行展开，采用聚合—转移—配置过程实现。MLFMA的计算和存储复杂度由传统MoM 的O（N2）～O（N3）量级降低为O（NlogN）量级，其中N为数值计算未知量数。

1.2 稀疏近似逆预条件技术

对矩阵方程进行预条件处理，可以提高迭代求解收敛速度。传统构造稀疏近似逆（SAI）预条件矩阵M时，需要对矩阵逐列构造，即需要求解N个最小二范数问题，这对于电大尺寸问题而言计算量极大［10］。而分析介质问题时，分界面上将同时定义等效电流和磁流未知量，进一步加大了计算复杂度。本文提出了基于几何分组信息的SAI 预条件技术，具体步骤如下：

步骤1确定预条件矩阵的稀疏化模式。本文采用MLFMA 框架下的附近组矩阵相同的矩阵分布。

步骤2获取用于构造SAI 矩阵的阻抗矩阵元素。首先，得到与之相关的附近组及其附近组的附近组所包含的矩阵元素，然后，利用近场耦合强弱关系和设定阈值对矩阵元素进行稀疏化。

步骤3完成每个分组内基函数对应的最小二范数运算：

式中：I、ej分别为全局单位矩阵和分组单位矩阵；为全局阻抗矩阵A的稀疏化模式；mj为M中第j组基函数对应的子矩阵为矩阵的Frobenius范数。

步骤4合并所有组元素得到预条件矩阵。

该方法的优点是：1）按分组方式生成预条件矩阵会极大减少最小二范数的计算次数；2）非常容易按组实现并行化。

1.3 球谐展开多层快速多极子算法

MLFMA 通过将散射源对场点的作用分解为一系列平面波的传播行为，实现了远区作用的快速计算和降低存储，但是需要存储角谱空间中各基函数的聚合、配置因子。介质问题中基函数个数多，导致角谱的存储量急剧增加，本文引入一类基于谱域球谐展开的多层快速多极子算法（SE-MLFMA）［11］来减少内存占用。该方法首先将MLFMA 展开项分为两部分：聚合转移因子和配置因子；然后分别进行球谐展开，展开系数为其特征值；最后再利用球谐函数之间的计算实现平面波的传播过程。MLFMA 中的远区矩矢相乘转化为下述形式：

式中：p为截断系数为第i个配置因子的特征值；为将第i个散射源聚合至组m′中心，进而转移至组m中心的聚合转移因子的特征值；Gm为第m个分组。

SE-MLFMA 将聚合、配置因子在谱域中的样本值存储转化为对其特征值的存储，存储复杂度将得到显著降低，而计算复杂度则与MLFMA 一致。考虑到实际剖分单元（如三角形网格）数远小于基函数个数，因此，将其转化为对网格单元的存储，可以进一步改进存储效率。

2 数值算例

通过以下算例验证本文方法的准确性和高效性，所有算例均在DELL PowerEdge R730 服务器上完成（配置为CPU Intel Xeon E5-2687W，主频3.0 GHz，共24 核，内存512 GB）。

2.1 带罩九元偶极线阵辐射仿真

第1 个模型为介质球壳内的9 单元偶极线阵辐射问题，如图2（a）所示。球壳内、外半径分别为1.20 m 和1.28 m，相对介电常数为εr=2+1i。线阵位于球内中心，排列和朝向均为x轴方向，单元间距为0.25 m。工作频率为300 MHz，阵元等幅同相馈电。如图2（b）所示，计算所得远区辐射场与MIE级数结果［12］吻合很好。

图2 介质球壳内9 元偶极线阵远区辐射场Fig.2 Far-field radiation of the dipole linear array of nine elements in a dielectric spherical shell

2.2 阵列天线-天线罩仿真

天线罩高460 mm，罩壁等厚5 mm，天线罩介质材料εr=3.3，tanδ=0.005，如图3 所示。半波振子阵列单元数为208，朝向为x轴方向，阵元中心间距8.8 mm，形成半径约为75 mm 的圆形口径，振子单元中心馈电。阵列距离反射面4.4 mm，反射面距离天线罩底部60 mm。设定频率为17 GHz，离散得到未知量数约81 万。仿真得到yoz平面的和差方向图如图4 所示，并与商业软件FEKO 仿真结果进行了对比。其中，和方向图最大峰值增益分别为26.19 dB 和26.42 dB（FEKO），差波束方向图也吻合很好。JMCFIE 方程（α=0.9）和PMCHW 方程，以及本文提出的SAI 预条件技术和不采用预条件时的收敛曲线，如图5 所示。可以看出，SAI 预条件极大地降低了迭代次数，减少了计算时间。SE-MLFMA 的计算时间和内存占用情况见表1。球谐展开技术将聚合配置因子所占内存减少了2/3，提高了算法对电大尺寸问题的求解能力。

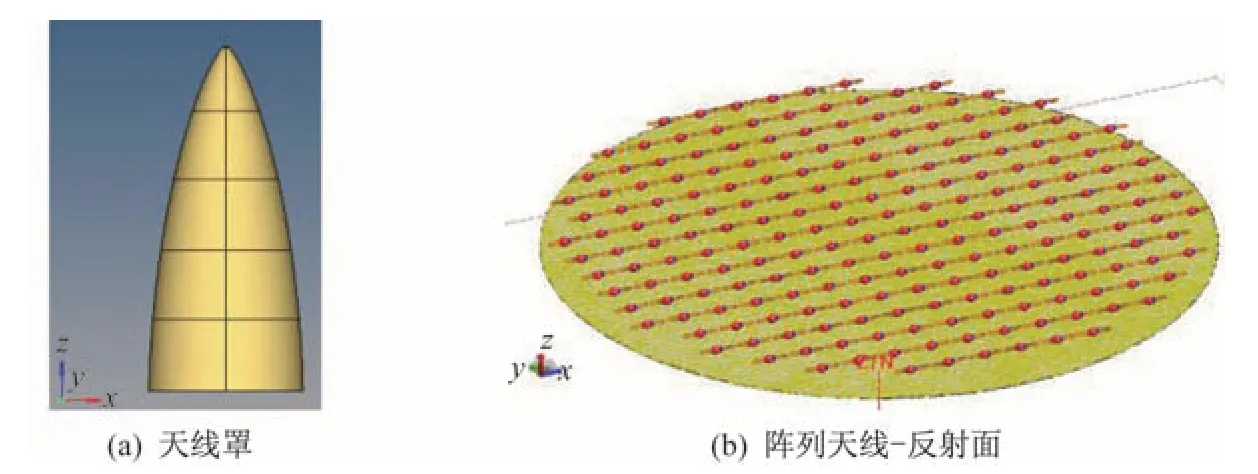
图3 阵列天线-天线罩几何示意图Fig.3 Geometric sketch of array antenna-redone

图4 增益方向图Fig.4 Gain pattern

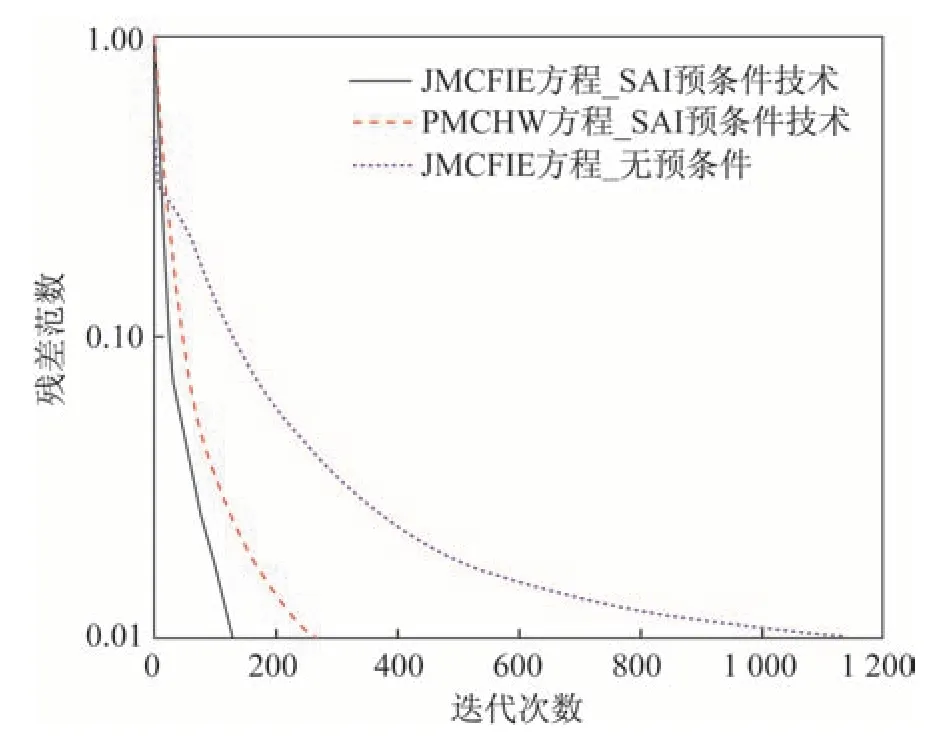
图5 迭代收敛性比较Fig.5 Comparison of the Iterations

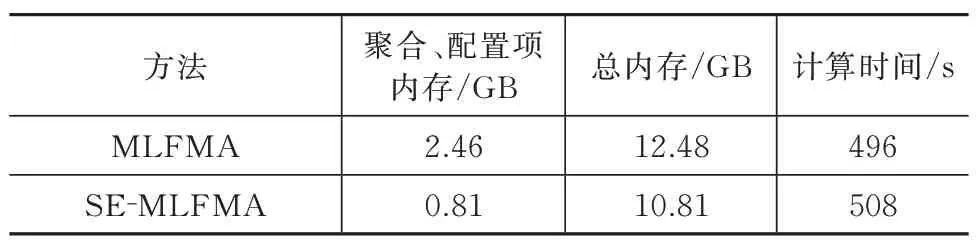
表1 采用球谐展开前后计算参数统计Tab.1 Statistics of calculated parameters before and after spherical harmonic expansion

2.3 电大尺寸天线罩问题

考察频率75 GHz 时带罩阵列的辐射特性。应用第2 个算例的天线罩和反射板模型，保持阵列单元数不变。调整半波振子间距2 mm，阵列到反射面距离1 mm，所有单元等幅同相馈电。仿真得到了增益方向图，如图6 所示，计算时间和内存占用情况，见表2。可以看出，在单台小型服务器上完成了电尺寸超过100λ0天线罩的电特性仿真。

表2 计算参数统计Tab.2 Statistics of calculated parameters

3 结束语

本文针对电大尺寸天线罩电特性分析的高效数值计算方法，从加速计算和减少内存需求两方面开展研究工作。基于导体介质复合结构的表面积分方程法，研究了积分方程构建形式，提出了一种MLFMA 分组框架下的SAI 预条件技术，利用近场信息和设定阻抗元素阈值的方式来加速构建预条件矩阵；进一步引入球谐展开技术减少对多极信息的存储。数值结果表明：改进后的积分方程法具有较高的计算精度和计算效率，可用于各类天线阵列-天线罩电磁特性的一体化建模分析。