多种工质下螺旋波等离子体源波场结构数值模拟

谢 平，段朋振，李益文，翟旭升

（1.空军工程大学航空机务士官学校，河南信阳 464000；2.空军工程大学等离子体动力学重点实验室，陕西西安 710038）

0 引言

电推进系统被广泛地用于卫星推进及姿态控制中，其中部分卫星已经飞越月球用于深空探测计划［1］。相比于化学推进器，电推进的优势在于其推进工质的利用效率更高［2］。对于典型的液体双基推进剂，排气速度局限于2.9～4.5 km/s 范围内；相比较而言，电推进系统通过电场或磁场直接加速推进剂［2-3］，排气速度能够达到3～100 km/s 范围［2-5］。化学推进器的比冲特点，从根本上限制了其执行某些特殊类型任务的能力。与此相比，更高排气速度、更大质量比和更高比冲的电推进器成为了人们关注的热点，其成熟的应用将为空间飞行器提供更大的装载量，或者完成之前不可能完成的探索任务。

目前，国际上应用较多的电推力器主要包括霍尔推力器、离子推力器［6］，是在轨空间飞行器的主要推进系统，其优势在于大比冲和高效率。此外，还有电弧推力器、磁等离子体动力推力器、脉冲等离子体推力器、场发射离子推力器、螺旋波推力器等其他类型的电推力器。

螺旋波放电经历了由容性放电向感性放电，以及由感性放电向螺旋波放电的模式转换［11-13］。在低磁场或者低功率条件下，天线的静电电位以容性方式将功率耦合到近壁面气体，并将气体击穿为弱电离等离子体。随着功率的增加，天线的波动磁场在管内部诱导出强电场，等离子体密度跃升，但是并不足以维持波耦合模式，即不能满足螺旋波传播的色散关系，放电进入非共振感性耦合等离子体（ICP）阶段，进一步增加功率导致密度增加，当等离子体密度满足色散关系，产生螺旋波。密度发生第二次跳变，使得放电模式转变为螺旋波放电。当放电进入螺旋波放电模式后，特定长度的天线激发出波长一定的螺旋波，此时等离子体密度与磁场强度成比例［14-15］。

在较低压强范围，无碰撞加热机制为主要功率耦合机制，而在高压强范围，电子-中性粒子的碰撞频率更高，碰撞加热占据优势［12］。无碰撞电子加热通过波的电磁场和等离子体电子之间直接或间接相互作用产生，无碰撞加热机制非常复杂，国际上已争论多年，目前仍未达成一致见解［16-18］。CHEN等［12］提出了加速电离电子的朗道阻尼作用，SHAMRAI等［16］提出不同磁场强度下TG 波-螺旋波的模式耦合机制，CHARLES 等［19］提出径向密度梯度引起对射频功率的共振吸收、径向局部螺旋波（RHL）在轴向形成驻波形态等。

虽然螺旋波放电机理复杂，但学者们从未放弃对于真理的探究，大量实验的开展推动了螺旋波等离子体的应用，领域内专家相继编写多种计算机程序，对螺旋波等离子体内部以及放电过程进行计算分析。其中ARNUSH 等［20-21］编写的HELIC 程序，在国际上知名度较高，领域内专家学者比较认可。本文采用该HELIC 程序对螺旋波放电进行数值模拟研究，初步探索放电机理，研究不同工质条件下等离子体的波场结构，为实验系统优化及实验方案设定奠定理论基础。

1 计算模型

1.1 HELIC 程序简介

HELIC 程序可用于射频等离子体源和放电实验的设计验证。结合边界条件，该程序通过求解4个径向耦合微分方程来获得2 个独立的波，即螺旋波（Helicon Wave）和 TG 波（Trivelpiece-Gould Wave），输出等离子体中波磁场、波电场、电流密度、相对功率沉积密度等特征参数。HELIC 程序包含2个基本设定：1）外部直流磁场在轴向和径向必须是均匀的；2）忽略等离子体的激发和输运过程。

假设等离子体是周向对称、轴向均匀的圆柱型等离子体，磁场强度、电子温度、等离子密度和气体压强等参数可根据实验结果或目标结果设定。该程序包括以下效应：电子-中性粒子、电子-离子的碰撞；n（r）、Te（r）、p0（r）任意径向分布；有限电子和离子质量；端板反射效应；任意闭合天线结构；位移电流等。

1.2 波场方程

对于径向非均匀等离子体，麦克斯韦方程的频域表达式为［22］

不同平衡氨基酸对严重腹部创伤患者术后营养代谢及预后的影响 ………………………………………… 郑姣妮等（10）：1364

式中：E为波电场；B为波磁场；J为天线电流密度；ω为螺旋波频率（射频频率）；μ0为真空磁导率；ε为低温等离子体介电张量，

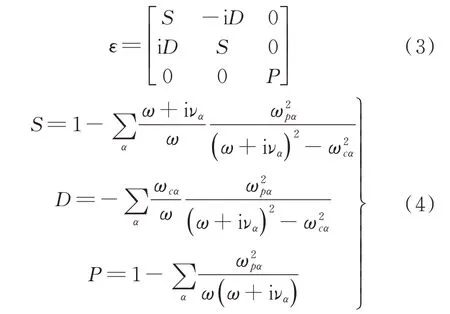
式中：下标α为粒子种类（ion 为离子，ele 为电子）；为等离子体频率；ωcα=qαB0/mα为粒子回旋频率；να为粒子间碰撞频率。假设等离子体中离子是单电荷，即qion=-qele=|e|。

利用傅里叶变换得到波场耦合微分方程组为

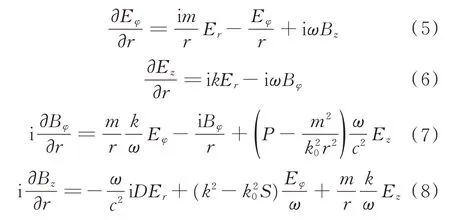
式中：k0=ω/c；m为角向模数。式（5）～式（8）组成了封闭集合，可以用标准方法数值求解。

1.3 边界条件

用Vi（r）表示波磁场B、电场E或电流密度J的任意分量，vi（r）为其基函数，Kφ为天线电流密度φ分量的傅里叶变换。波场分量Vi（E，B，j）可表示为

式中：A1和-A2为待确定幅值；x为轴向z、径向r和角向φ3 个方向的分量。结合边界条件，可以计算得到代数方程的解为

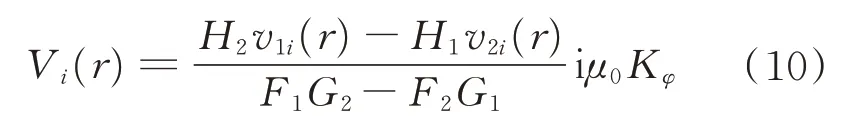
式中：参数F、G、H为包括贝塞尔函数和基函数的代数表达式。

从式（10）中可以看出，解由3 部分组成：1）波场与天线电流的傅里叶变换Kφ成比例；2）波场与独立于天线性质的位移电流D成反比例，无阻尼情况下，等式D=0 精确地给出螺旋波和TG 波耦合模式的色散关系；3）分子给出波场的径向变化。一旦计算得出给定密度分布下的基函数，对于任意天线结构和边界类型，可以迅速地完成式（10）的估算，其中，

式中：角标n为1 时代表螺旋波模式，n为2 时代表TG 波模式；bn，x、en，x、jn，x为波磁场、波电场和电流密度的基函数。

对于半径为a、长度为2l的圆柱型等离子体放电区域，功率吸收相对密度沿径向和轴向的分布计算式为

1.4 参数设置

图1 为，数值模拟的物理模型，天线尺寸及类型、工质类型、驱动频率等均与文献［23］中的实验设置相一致，具体尺寸以及相关参数见表1。取两种气体压强条件分别为0.266 Pa 和1.064 Pa，工质气体类型分别为氩气、氦气、氮气，电子温度为4.5 eV，磁场强度为200 A/m，驱动频率与实验保持一致为13.56 MHz，天线类型为半波螺旋天线（Half Helix Antenna），螺旋波角向模数m=+1。设定中心轴处等离子体密度n0为5×1018m-3，密度沿轴向均匀，沿径向服从典型抛物线型分布，如图2 所示，服从如下三参数方程式：

式中：s=2；t=1；fa=0.1。

图1 计算模型Fig.1 Computation model

表1 计算参数设置Tab.1 Computation parameter settings

图2 等离子体密度沿径向分布曲线Fig.2 Distribution curve of plasma density in the radial direction

2 结果与分析

2.1 波磁场

等离子体内波磁场各分量沿径向变化特征如图3 所示。在图3 中：气体压强p分别为0.266 Pa 和1.064 Pa；径向、角向和轴向分量有不同的分布特征，但在径向边界处都趋于零，这与边界条件限制相一致。

对于角向分量Bφ和径向分量Br，氩气与氮气的分布非常接近，并且对于压强更为敏感，在径向中心处（r=0）随压强增加，增幅相比于氦气更为明显。随压强的改变，轴向分量Bz在径向r=0.015 m 位置处的峰值有所变化，氮气增加而其他两种工质的变化趋势相反，曲线逐渐分离。

2.2 波电场

波电场轴向分量Ez相比于其他两个方向的分量小很多，此处不再讨论。径向分量Er和角向分量Eφ沿径向的分布特征，及在不同压强条件下的表现如图4 所示。Eφ沿径向呈现递减趋势，在边界处为0。在低压强条件下，3 种工质气体Eφ分量保持一致，曲线基本重合，而压强增加到1.0 Pa 以上时，径向中心处最大值出现分歧。

图3 波磁场分量沿径向分布特征Fig.3 Radial profile of wave magnetic field components

径向分量Er由径向边界条件决定，Er在内部（r＜0.044 m）电场强度较低，与角向分量最大值相当，并在径向边界处迅速增加达到峰值。从图中可以看出，压强增加限制了径向边界处Er的峰值，1.064 Pa 压强下相对于0.266 Pa 减小了近50%，原因是压强的增加导致波所受阻尼增强，TG 波被更有效地局限于径向较窄的边界处。氦气等离子体的Er分量在径向边界处的峰值更为突出，更有利于等离子体在径向的输运。

图4 波电场分量沿径向分布特征Fig.4 Radial profile of wave electric field components

2.3 电流密度

对于电流密度，低压强下3 种工质气体的径向分布特征较为接近。在压强达到1.0 Pa 以上时，3种气体的部分分量出现较大分歧，如图5 所示。从图中可以看出，3 个分量中，轴向分量Jz对于压强变化更为敏感，在r=0.01 m 的峰值随压强增加呈降低趋势，压强达到1.0 Pa 以上时，氩气和氮气工质的峰值已不在，而氦气则保持着三者中的优势地位。

p=0.266 Pa 时，3 种气体工质的径向分量Jr分布特征非常接近，3 条曲线基本重合。随着压强增加，Jr在径向中心处的最大值有所变化，其中氩气工质略有降低，氦气降低更多，而氮气却明显升高。这种变化特征与图5 中Er在径向r＜0.02 m 内的特征相似，即p=0.266 Pa 时3 种气体的Er曲线基本重合，当压强增加到1.064 Pa 时，氮气在径向中心处（r=0）的值有所增加，而另外两种气体则减小。说明波电场径向分量决定了电流密度径向分量在内部的表现，由于等离子体边界设定为绝缘界面，虽然Er在边界处达到峰值，径向电流密度Jr在此处却趋于0。

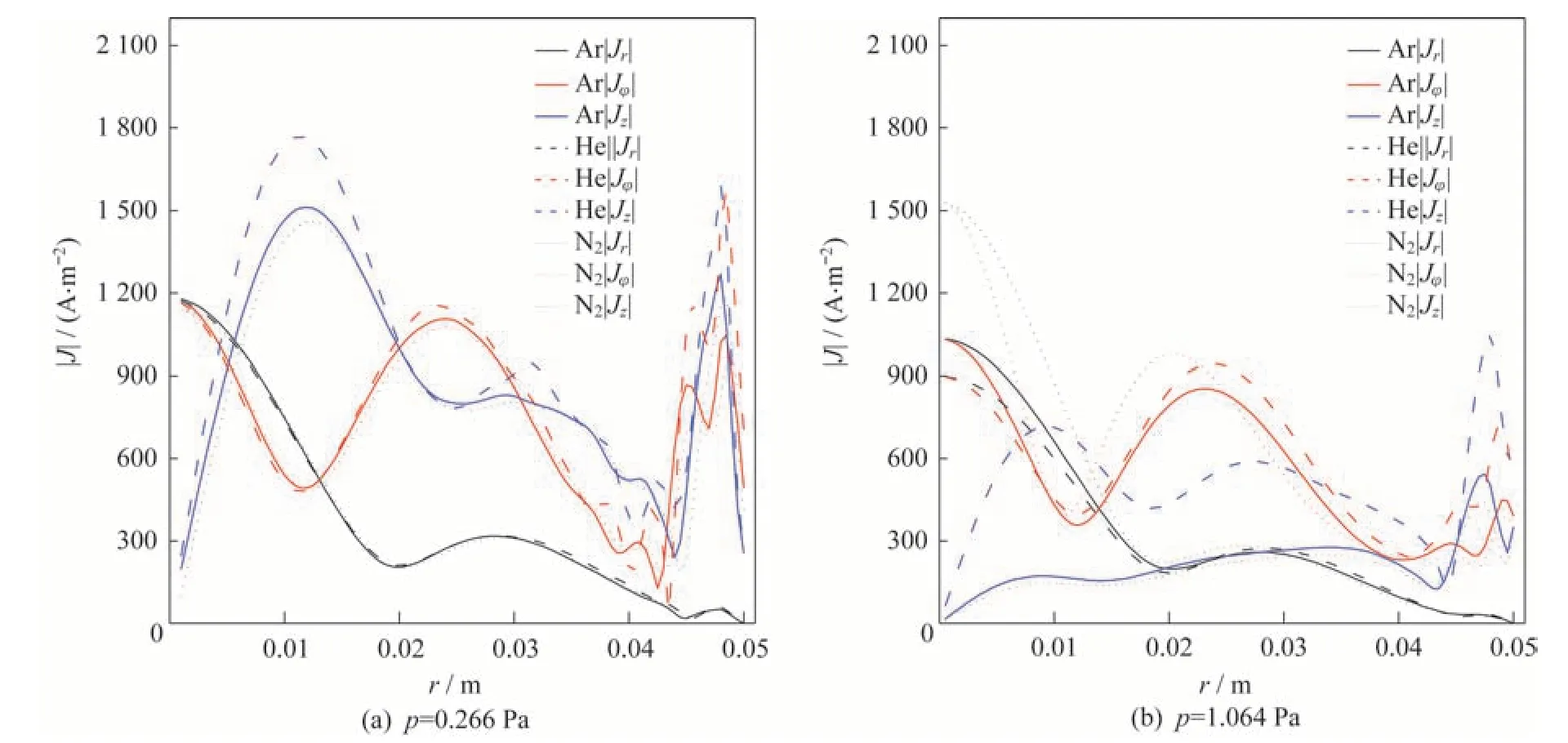
图5 3 种工质气体放电中电流密度分量沿径向分布特征Fig.5 Radial profile of current density components

角向分量Jφ在低压强下曲线基本重合，随压强增加径向边界处峰值降低明显，内部两处峰值稍有降低，只有氮气在径向中心处的峰值有所增加。其特征与Jr非常相似，同样图4 中Eφ的变化表现为，氮气在径向中心处的值有所增加，另外两种气体略减小。

2.4 功率沉积密度

3 种工质气体在两种压强条件下得到的功率沉积密度沿径向的分布特征如图6 所示。

图6 功率沉积密度沿径向分布特征Fig.6 Radial profile of relative power deposition

从图6 中可以观察到，3 种气体放电下，靠近径向中心（r＜0.01 m）范围内，曲线差异较为明显，且在不同的压强条件下各工质的优势不同。压强为0.266 Pa 时，氦气的功率沉积密度要高于氩气和氮气，而后两者的曲线分布则非常接近；随着压强增加到1.064 Pa，氮气放电下的功率沉积密度超过其他两种气体，而氦气则低于氩气。其实，当压强增加到0.6 Pa 以上时，功率沉积密度优势向径向边界处转移［23］，因此1.064 Pa 压强条件下径向中心处这种差异显得不再重要了。

由实验及仿真研究结果得知［23］，适当增加气体压强，可有效提高螺旋波放电强度和等离子体密度。但是当压强增加到一定程度，达到1.0 Pa 以上时，放电进入一个类饱和状态，这是由于TG 波在更高压强下所受阻尼更强，被局限于径向边界，基本上是一种表面波，大部分功率通过TG 波沉积于径向边界处，其向等离子体内部的输运受限，进而影响了放电强度的进一步增强。从图6 中亦能观察到同样的特征，即随压强增加径向边界处的功率沉积密度分布占据更多的优势。

3 结束语

综合以上结论，可以看出不同工质气体等离子体内部波场结构有所差异，且不同工质的部分波场分量对于压强的敏感程度不同，波电场的角向分量和径向分量变化特征与电流密度的对应分量特征相一致。氦气等离子体的Er分量在径向边界处的峰值更为突出，更有利于等离子体在径向的输运，波电场径向分量决定了电流密度径向分量在内部的表现。

另外，数值模拟通过设置0.266 Pa 和1.064 Pa两个压强条件，分析波场结构特征，验证了压强对于波阻尼的影响。压强的增加导致波所受阻尼增强，TG 波被更有效地局限于径向较窄的边界处，其向等离子体内部的输运受限，进而影响了放电强度的进一步增强，与实验结论相一致。

由于HELIC 程序默认的“天线电流”相同，同样为增强对比性，对于3 种工质气体，在边界条件的设置和等离子体密度设定上也一致。因此，在此处本文不便探讨三者放电的强度或难易程度，仅对等离子体内部波场结构做探讨，为放电机理研究奠定基础，为实验数据提供一定的理论支撑。