双重代价敏感随机森林算法
2021-01-16周炎龙孙广路
周炎龙 孙广路



摘要:针对分类器在识别不平衡数据时少数类准确率不理想的问题,提出了一种双重代价敏感随机森林算法,双重代价敏感随机森林算法分别在随机森林的特征选择阶段和集成投票阶段引入代价敏感学习。在特征选择阶段提出了生成代价向量时间复杂度更低的方法,并将代价向量引入到了分裂属性的计算中,使其在不破坏随机森林随机性的同时更有倾向性地选择强特征;在集成阶段引入误分类代价,从而选出对少数类数据更敏感的决策树集合。在UCI数据集上的实验结果表明,提出的算法较对比方法具有更高的整体识别率,平均提高2.46%,对少数类识别率整体提升均在5%以上。
关键词:随机森林;不平衡数据;特征选择;代价敏感
DOI:10.15938/j.jhust.2021.05.006
中图分类号:TP181 文献标志码:A 文章编号:1007-2683(2021)05-0044-07
0 引言
随着大数据时代的来临,数据呈现数量多、不平衡等特点,即一个类样本数量远多于另一个类的样本数量[1],如何将其正确的分类是一种重要的数据分析技术。类别不平衡的数据普遍存在于现实生活的许多应用中。例如,用于疾病诊断预测的病历数据中,许多少见却非常重要的疾病样本数远小于正常或常见的疾病样本数[2];用于互联网人侵检测的样本数据中,正常的样本数远多于人侵的样本数。若将传统分类器应用于这些场景而不对类别的不平衡性做任何处理,就会使得多数类淹没少数类(少数类往往是更重要的),得不到好的分类效果。因此,类别分布的不平衡问题是数据分类中很重要的一类问题。
针对类别不平衡数据的分类问题,研究人员在数据预处理和分类器模型算法2个方面提出很多改进方法。其中,在数据预处理方法中又分为数据分布和特征选择。特征选择的目的是从全部特征中选择更适合于类别不平衡数据、能反映类别不平衡特点的子集来构建分类器模型,从而使得分类器在类别不平衡的前提下达到较好的性能[3]。数据分布调整主要通过数据重采样或数据分组等手段使得类别在一定程度上达到平衡,从而消除类别不平衡问题。
除了通过特征选择、数据分布调整来降低类别不平衡对分类算法的影响,还可以直接在算法层面,通过设计适用于不平衡数据特征的模型训练算法来解决类别不平衡问题。这方面的研究工作主要有代价敏感学习,集成学习以及其他算法,如关联分类算法、K近邻算法等。
1 相关工作
随机森林是由Breiman[4]提出的一种集成学习算法,通过组合若干个单分类器的分类结果,从而对测试样本的类别做出分类。该算法与单个分类器相比,具有更好的分类效果和泛化能力。研究人员在随机森林不同阶段提出了优化和改进方法。
在特征选择阶段,Paul等[5]提出了一种改进的随机森林分类器。根据重要特征和不重要特征的个数,迭代地去除一些非重要的特征,构造了一个新的理论上限,即加入到森林中的树的个数。以保证分类精度的提高,并且算法收敛于一组减少但重要的特征。Zhou等[6]提出一种特征代价敏感随机森林算法(Feature Cost-Sensitive Random Forest,FCS-RF),该算法将代价敏感学习引入随机森林算法的特征选择阶段,针对每棵决策树通过其OOB(Out ofBag,OOB)数据计算出不同特征下的分类准确率,再通过提出的算法计算出代價向量,在不破坏随机性的同时使随机森林在选择特征时会更倾向于代价高的特征(即分类准确率更高的特征)。然而该方法在特征间没有明显强弱关系的时候就会退化为普通的随机森林算法。并且该方法没有考虑特征间的相对关系,并且生成特征向量的时间复杂度过高。
在集成投票阶段,用OOB数据计算出识别准确率,再通过不同的算法计算出每棵决策树的权重,从而在最终样本分类时使分类结果更倾向于分类准确率高的决策树的分类结果[7-8]。这些方法在数据高度不平衡时,虽然能有较高的整体识别准确率,但是对少数类的识别准确率却并不理想。Xie等[9]将加权随机森林和平衡随机森林相结合,通过抽样技术与成本敏感相结合引入随机森林集成投票阶段的方法可以在保证整体识别准确率的同时提升少数类的识别准确率,但是该方法在时间和空间上消耗过大。
随机森林算法虽然具有较好的分类效果和泛化能力,但是在数据不平衡度较大时,分类效果却并不理想,为此可以引入代价敏感学习来解决此问题。目前对代价敏感学习的研究主要集中在代价敏感间接学习和代价敏感直接学习2个方面[10]。代价敏感间接学习主要是通过对数据集特征空间的重构,间接地进行代价敏感学习,从而改变已有数据集的不平衡度,代表性的方法是代价敏感元学习[11]。代价敏感直接学习则是在传统学习算法的基础上引入代价敏感因子,通过改进分类器模型的内部构造,使基于最小错误率的分类器转化为基于最小代价的代价敏感分类器。目前,主流的分类算法如人工神经网络[12]、朴素贝叶斯[13]、SVM[14-16]、决策树[17-18],AdaBoost[19-20]等都有着相应的代价敏感扩展算法。虽然近些年深度学习成为大家关注的焦点,并在各个领域效果显著。但其可解释性的探索仍处于初级阶段[21],并且模型的训练需要大量的数据,在样本数量不足时会发生欠拟合的现象。
2 基于双重代价敏感的随机森林算法
2.1 代价敏感的引入
目前代价敏感学习算法主要针对二分类问题,当目标被错分成其他类的代价有较大差异时,区分这些代价是必要的,即使被错分类,也希望被错分到代价小的类上。针对二分类问题,代价敏感一般用代价矩阵(见表1)表示分类器分错时要付出的代价。c0为少数类,c1为多数类,C(i,j)表示将类别j错分类为i所要付出的代价。
2.2 双重代价敏感随机森林(Double Cost SensitiveRandom Forest,DCS-RF)
双重代价敏感随机森林算法(DCS-RF)主要分为生成代价向量、构建决策树和集成投票3个阶段,如图1所示。
随机森林算法对数据集随机并有放回地抽样N次作为一棵决策树的训练集。其中未被选择到的数
2.2.1 代价向量的生成
在生成代价向量阶段,FCS-RF算法利用随机森林OOB数据计算出的误差变化来计算特征的重要度得分,从而计算出代价向量,但其所耗时间过长。因此本文提出的获取代价向量的方法仅利用OOB数据的准确率作为标准,经实验证明耗时更少。具体步骤如下:
1)初始化代价向量q=[r1,r2,…,rn],n为特征数量。设定阈值ω和权值向量λ=[λ1,λ2,…,λn],其中向量λ中的数值为[n,n-1,n-2,…,1],n为特征数量。因此权值向量λ=[n,n-1,n-2,…,1]。设置m为每次选取的特征数量,常设m=■。利用OOB数据对每棵决策树进行测试。设A为准确率,当Aj≥w,j=1,2,…,ntree时(其中ntree为决策树的数量),将第j棵树中所选择的所有特征按照从根结点到叶子结点的顺序排序,将各结点中所选的用作分裂属性的特征构成集合Fj。对于集合Fj中所有的特征,通过式(3)依次计算得到特征i的特征系數ri。
2.2.2 分裂范式的构建
在构建决策树阶段,将代价向量引入属性分裂Gini指数的计算中,得到新的Gini指数CGini(CostGini index)。
特征系数越低的特征对应的CGini的不纯度越高,其作为分裂准则的效果越好。
2.2.3 集成投票
在决策树的集成阶段引入误分类代价,将平均误差代价(average error costs,AEC)作为集成标准,获得对于少数类更敏感的决策树集合,构建完整的DCS-RF算法。AEC可表示为
针对每棵决策树j,分别计算对应的平均误差代价:其中x10表示伪正例;x01表示伪反例;N是样本总数量。
2.2.4 算法步骤
整体算法步骤如算法1所示。
算法1 双重代价敏感随机森林算法
3 实验结果与分析
3.1 实验设置
本文选择了UCI的8组数据集,并对其中的多分类数据集进行调整,转化为二分类数据集,具体描述如表2所示。8组数据分成2组,一组通过生成的代价向量中各个特征间的数值关系对数据集的特征强度进行了高、中、低的标注,检测算法在不同特征强度数据集上的识别效果。并对FCS-RF和DCS-RF算法生成代价向量的时间进行比对。
另一组根据数据集的特征强度进行划分,分别从高、中、低特征强度的数据集中各取出一组数据进行不平衡处理,使其呈现出5种不同的不平衡度如表3所示,对本方法在不同平衡度上的分类效果进行实验验证。在实验开始前,需要对代价矩阵进行赋值。假设少数类为c0,多数类为c1。那么C(c1,c0)和C(c0,c1)就分别代表把少数类错分为多数类的代价和将多数类错分为少数类的代价。本文更加关注的是针对不平衡数据的识别率,即对少数类的识别准确率,所以C(c1,c0)的代价应该高于C(c0,c1)的代价。这样我们就将C(c0,c1)的代价设为1,假设C(c1,c0)的代价是2就说明将c0错分为c1的代价是将c1错分为c0的代价的两倍。通过调节C(c1,c0)的值N,分别计算其等于1,2,4,8,16,32,64时的结果。通过实验计算发现C(c1,c0)=32时效果最佳。
同时对于决策树的数量理论上是数量越多识别效果越好,但是消耗的时间也会增加,综合考虑设置决策树的数量为100,因为在决策树的数量为100时即可达到分类精度。
3.2 结果分析
2种算法生成的代价向量如表4所示,分别选取高、中、低特征强度的数据集Wine,Cancer,Jain,Diabetes进行对比实验。可以看到在高、中特征强度的数据集中,本文的特征选择方法可以更加快速高效的挖掘出高强度特征。虽然不能保证特征的强弱排序都与FCS-RF所产生的顺序相同,但高、中、低强度特征集合中的特征元素却相同。同时随着数据维度的增加,DCS-RF在代价向量的生成速度上更占优势如表5所示,速度提升普遍在2倍以上,数据维度是训练集数据量乘以特征维度。
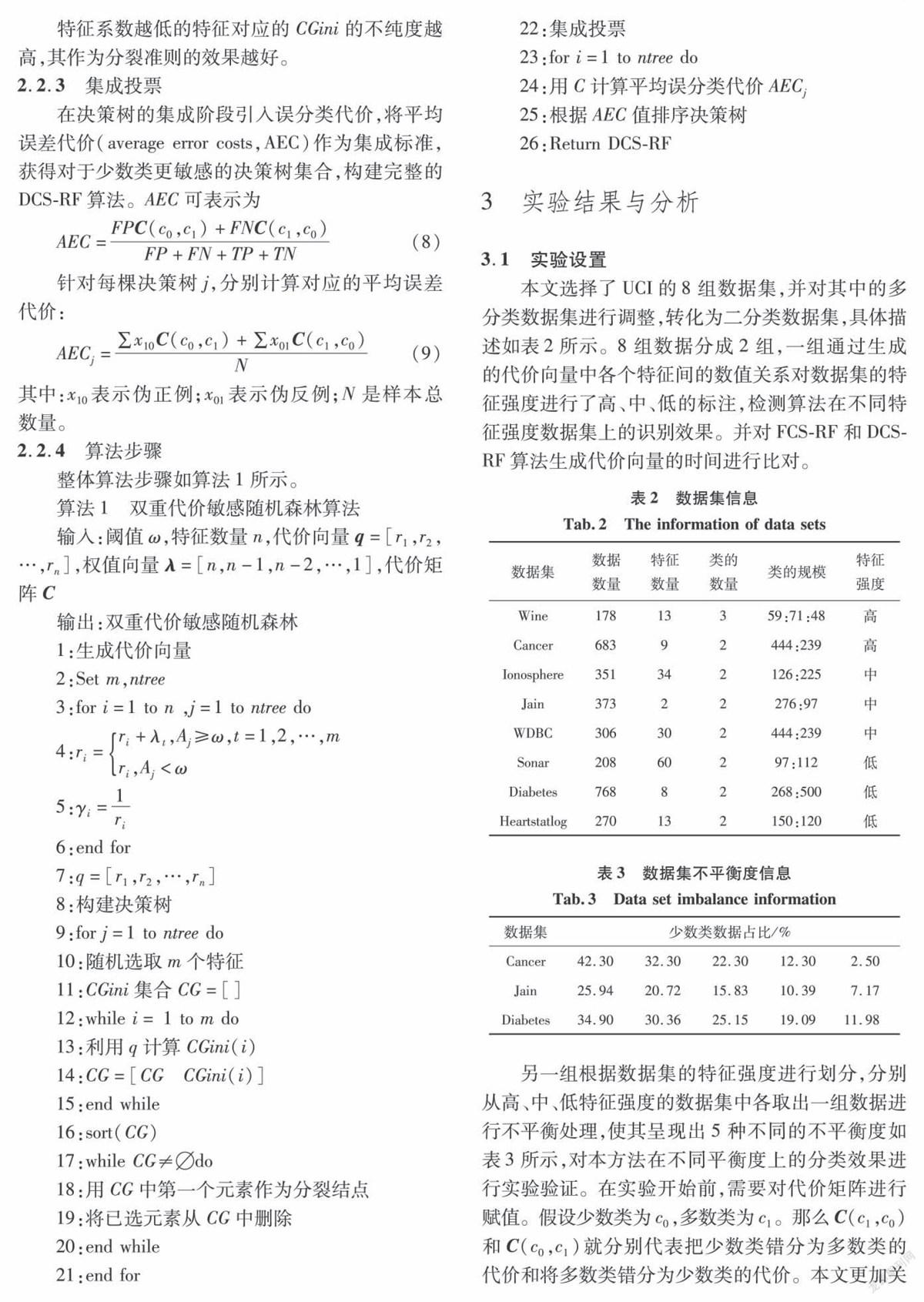
在不平衡数据分类问题中,关注整体识别准确率的同时更应关注少数目标类的分类准确率。本文选择如下指标评价分类算法:准确率(accuracy),召回率(recall)和F-measure。分别对支持向量机(SVM),K最邻近(KNN),随机森林(RF),特征代价随机森林(FCS-RF)和本文提出的双重代价随机森林(DCS-RF)算法进行对比。
对KNN分类标准采取的是欧氏距离,K值设置为2。SYM中核函数采用RBF,迭代次数为50,松弛变量为20,惩罚因子0.6。表6显示了5种不同的分类算法在8组不同特征强度的数据集上的整体识别准确率。可以看出在具有高特征强度和中特征强度的数据集上,DCS-RF和FCS-RF算法的识别率明显高于其他的分类算法。在低特征强度的数据集上,FCS-RF算法对低特征强度数据不敏感,所以会退化成普通的随机森林算法,其结果也与随机森林没有任何区别。由于DCS-RF算法在集成阶段引入误分类代价,所以在处理低特征强度的数据时,整体识别准确率仍能高于随机森林和FCS-RF算法。同时在绝大多数的数据集上明显高于其他4种分类算法,有着更高的识别准确率。另外我们可以注意到,虽然在Wine数据集上随机森林,FCS-RF和DCS-RF达到了接近100%的识别准确率,但是经过实验证明,3种分类算法到达该准确率使用的决策树数量完全不同,比值为10:7:5。由此可以看出相比于随机森林和FCS-RF两种算法,DCS-RF达到相同的识别效果所使用的决策树数量更少。
通过表7、8中各类算法在数据集上的召回率和F-measure可以看出,DCS-RF算法因为在决策树的集成阶段引入了代价敏感学习的原因,所以其对少数类样本的分类效果始终优于其他的算法。
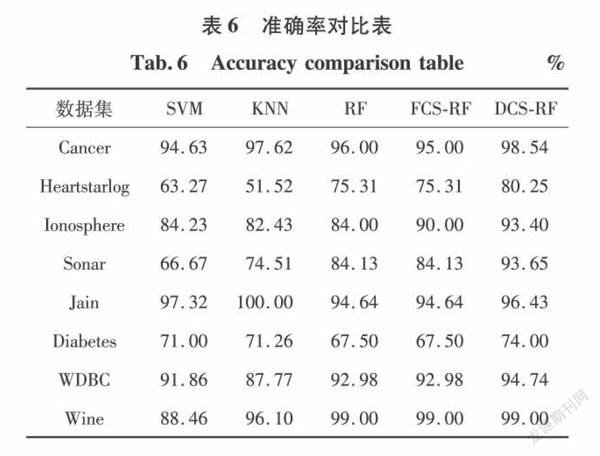
为了验证算法在不平衡数据上的识别效果,图2显示了5种算法在Cancer,Jain和Diabetes数据集的不同平衡度上的召回率。数据的不平衡度分为5个级别,其中Cancer数据集中少数类占比分别是42.3%,32.3%,22.4%,12.4%,2.5%:Jain数据集中少数类占比分别是25.94%,20.72%,15.83%,10.39%,7.17%;Diabetes数据集少数类占比分别是34.90%,30.36%,25.15%,19.09%,11.98%。
通过图2(a)、(b)可以看出随着少数类所占比例的减少,RF及其变种算法对于少数类的识别率的波动幅度相对平缓。但是SVM和KNN算法的表现则并不理想。在图2(c)上可以看到,由于特征强度低,FCS-RF算法已经完全退化为RF算法,但基于随机森林本身良好的鲁棒性,其召回率的下降速度相对于SVM和KNN算法更平缓。同时也能看出DCS-RF算法由于在决策树集成阶段误分类代价的引入,其召回率始终高于其他幾种算法,即对少数类有着更高的识别率。
4 结论
针对分类器在识别不平衡数据时少数类准确率不理想的问题,提出了一种基于双重代价敏感的随机森林算法,分别在随机森林的特征选择阶段和集成投票阶段引入代价敏感学习,使其对少数类数据敏感。在保证特征间强弱关系的前提下,提出了获取代价向量耗时更少的方法;同时将代价向量引入到Gini指数中,在不破坏随机性的前提下,更有倾向地选择强特征;最后在集成阶段引入了误分类代价,使其在提高整体识别准确率的同时对不平衡数据中的少数类也有着较好的识别准确率。通过与SVM、KNN、随机森林、FCS-RF的实验对比,证明了本文提出的DCS-RF方法的有效性,在保证多数类准确的基础上提高了少数类的识别准确率。但该算法的代价矩阵需要人为去规定,如何自主生成合理且有效的代价矩阵则是下一阶段的研究目标。
参考文献:
[1]AU H,SALLEH M N B M,SAEDUDIN R,et al.ImbalanceClass Problems in Data Mining:A Review[J].Indonesian Jour-nal of Electrical Engineering and Computer Science,2019,14(3):1560.
[2]SUN Y,WONG A K C,KAMEL M S.Classification of Imbal-anced Data:A Review[J].International Journal of Pattern Rec-ognition&Artificial Intelligence,2009,23(4);687.
[3]宋智超,康健,孙广路,等.特征选择方法中三种度量的比较研究[J].哈尔滨理工大学学报,2018,23(1):111.
[4]BREIMAN L.Random Forests[J].Machine Learning,2001,45(1):5.
[5]PAUL A,MUKHERJEE D P,DAS P,CHINTHA R.ImprovedRandom Forest for Classification[J].IEEE Transactions on ImageProcessing,2018,27(8):4012.
[6]ZHOU Q,ZHOU H,LI T,et al.Cost-sensitive Feature SelectionUsing Random Forest:Selecting Low-cost Subsets of InformativeFeatures[J].Knowledge Based Systems,2016(95):1,
[7]杨宏宇,徐晋.基于改进随机森林算法的Android恶意软件检测[J].通信学报,2017,37(4):8.
[8]蔡加欣,冯国灿,汤鑫,等.基于局部轮廓和随机森林的人体行为识别[J].光学学报,2014,34(10):204.
[9]XIE Y,LI X,NGAI E W,et al.Customer Churn Prediction U-sing Improved Balanced Random Forests[J].Expert Systems withApplications,2009,36(3):5445.
[10]凌晓峰,SHENG,Victor,等.代价敏感分类器的比较研究[J].计算机学报,2007,30(8):1203.
[11]DOMINGOS P.Meta cost:A General Method for Marking Classifi-ers Cost-sensitive[C]//Proc.5th ACM SIGKDD InternationalConf.Knowledge Discovery and Data Mining,1999:155.
[12]ZHANG Z,LUO X,GARCA S,et al.Cost-Sensitive Back-propa-gation Neural Networks with Binarization Techniques in AddressingMulti-class Problems and Non-competent Xlassifiers[J].AppliedSoft Computing,2017(56):357.
[13]蒋盛益,谢照青,余雯.基于代价敏感的朴素贝叶斯不平衡数据分类研究[J].计算机研究与发展,2011,48(S1):387.
[14]DHAR S,CHERKASSKY V.Development and Evaluation ofCost-Sensitive Universum-SVM[J].IEEE Transactions on Sys-tems,Man,and Cybernetics,2015,45(4):806.
[15]周宇航,周志华.代价敏感大间隔分布学习机[J].计算机研究与发展,2016,53(9):1964.
[16]HIANMEHR A,MASNADISHIRAZI H,VASCONCELOS N,etal.Cost-sensitive Support Vector Machines[J].Neurocomputing,2019:50.
[17]齐志鑫,王宏志,周雄,等.劣质数据上代价敏感决策树的建立[J].软件学报,2019,30(3):114.
[18]LI F,ZHANG X.Cost-Sensitive and Hybrid-Attribute MeasureMulti-Decision Tree over Imbalanced Data Sets[J].InformationSciences An International Journal,2018(22):242.
[19]付忠良.多分类问题代价敏感AdaBoost算法[J].自动化学报,2011,37(8):973.
[20]ZELENKOV Y.Example-dependent Cost-sensitive AdaptiveBoosting[J].Expert Systems with Application,2019,135(11):71.
[21]成科扬,王宁,师文喜,等.深度学习可解释性研究进展[J].计算机研究与发展,2020,57(6):1208.
(编辑:温泽宇)
收稿日期:2020-07-08
基金项目:国家自然科学基金(61702140);黑龙江省留學归国人员科学基金(LC2018030);黑龙江省普通高校基本科研业务费专项资金资助(JMRH2018XM04).
作者简介:孙广路(1979-),男,博士,教授,博士研究生导师.
通信作者:周炎龙(1996-),男,硕士研究生,E-mail:zy1279751705@163.com.
