横向常磁场中铁磁圆板的主共振特性与静载效应

2021-01-16马冰冰胡宇达

振动与冲击 2021年1期

马冰冰，胡宇达

(1.燕山大学建筑工程与力学学院，河北秦皇岛 066004；2.燕山大学河北省重型装备与大型结构力学可靠性重点实验室，河北秦皇岛 066004)

电磁场环境中圆型板及其组合结构在工程实际中得到广泛应用，如：电机定子和转子的铁芯、电磁传感器结构件等，这些结构在电磁场中的耦合振动问题是决定机电系统安全运行的主要因素，因此，研究磁场中铁磁圆板的非线性振动问题既有理论意义，也可为工程实际中机电系统的动力学控制提供技术支持。并且在常磁场中，铁磁圆板结构受到静载荷作用，从而具有初挠度，对圆板非线性振动产生一定影响。

板的非线性共振问题已得到很多学者的关注。在20世纪90年代，Okajima等[1]对悬臂矩形板的共振频率与曲率和厚度变化的关系进行了研究。Oh等[2]对两种不同铺设角度悬臂复合板的非线性组合共振问题进行了实验研究，发现两种板的最大频率差为6%。近年来，Du等[3]对均匀载荷作用下阻尼夹层圆板的非线性超谐共振进行了研究，分析了解的稳定性和奇异性。高原文等[4]分析了在周期时变磁场中简支铁磁梁式板的非线性磁弹性动力特性与混沌现象。Xue等[5]研究了电磁弹性薄板的非线性无阻尼强迫振动，并分析了不同参量对主共振间隔、弹簧刚度特性和振幅跳跃现象的影响。胡宇达等[6-9]在矩形板方面，研究了四边简支功能梯度板的主共振，磁场环境中导电薄板的亚谐共振问题；在圆板方面，研究了磁场中旋转导电圆板的主共振与分岔问题以及超谐-组合共振问题。Chen等[10]研究了不同尺寸夹层板的固有频率，并讨论了其内共振特性。

近20年来，研究者们越来越关注静载荷下板结构的振动与屈曲问题。Yamaki等[11]同时考虑了初始挠度和初始边缘位移的影响，对均布横向载荷作用下夹层圆板的轴对称非线性振动进行了理论分析。Wang等[12]给出了静载荷下圆板的微分方程，得到了初挠度圆板非线性振动的周期解，并讨论了初始挠度对柔性板动力特性的影响。Du等[13]研究了均布荷载和周边荷载作用下夹层圆板的非线性振动,并用改进的迭代法求解振幅-频率-载荷特性关系，分析了两种载荷对夹层圆板振动特性的影响。同时，有些学者考虑了多场耦合的影响。王永岗等[14]研究了静态温度场中具有初挠度的双层金属薄板在周期时变横向载荷作用下的混沌运动。Hu等[15-16]研究了在静磁场作用下导电旋转圆板的非线性自由振动和主共振问题，分析了频率和振幅与静载、磁感应强度、转速等参数之间的关系。徐学平等[17]分析了偏心转子不计静载荷时和考虑静载荷时对转子系统振动特性的影响。另外，有一些学者对静载荷作用下板的屈曲问题进行了研究。王德禹[18]分析了受面内静载荷作用的矩形板在冲击载荷作用下产生的冲击屈曲，分析了静载荷、冲击载荷速度及初始挠度对板的屈曲特性的影响。Babich等[19]研究了预应力半空间板在静载作用下的初应力对弯矩的影响。

处于横向常磁场中铁磁圆板受到的磁体力为静载荷，静载荷下圆板产生的初挠度对系统振动产生影响。本文研究常磁场中铁磁圆板的主共振问题，得到圆板初挠度和扰动微分方程，利用多尺度法求解得出稳态运动下的幅频响应方程，并通过算例分析不同电磁参量对共振振幅的影响。

1 圆板磁弹性振动方程

1.1 圆板动能和势能

考虑处于外加法向磁场(Hn1为上表面磁场、Hn2为下表面磁场)中的各向同性铁磁圆板，在周边夹支的边界条件下，受到横向载荷Pz的作用。如图1所示，在圆板上建立柱坐标系(r,θ,z)。其中，r、θ、z分别为径向、环向、法向坐标；圆板厚度为h；半径为R；质量密度为ρ。

图1 磁场中铁磁圆板的力学模型

忽略面内位移情况下，设磁场中铁磁圆板板内任意一点的变形位移分量的表达式为

(1)

系统动能表达式

(2)

圆板弯曲形变势能表达式

(3)

圆板中面应变势能表达式

(4)

1.2 电磁力

根据磁弹性相互作用的理论模型[20]，得到磁场中铁磁圆板受到的磁体力

式中:Hn为圆板表面法线方向磁场强度;μ0为真空中的磁导率;μr为相对磁导率;χm为材料的磁化率，χm=μr-1。

运动圆板内部产生涡电流效应，依据电磁理论，运动物体所受洛伦兹力表达式为

f(fr,fθ,fz)=J×B

(6)

式中:J为忽略电场强度时的电流密度矢量，J=σ0(V×B);B为磁感应强度矢量，B=μ0μrH;σ0为电导率。

对式(6)沿板厚方向积分，可得电磁力矩为

(7)

(8)

横向磁场中，铁磁圆板受到的电磁力所做虚功表达式为

(9)

1.3 磁弹性振动方程

运用哈密顿变分原理得到

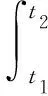
(10)

式中，δUP为横向激励力Pz所做虚功。

将式(2)～(4)、(9)代入式(10)中，且只考虑横向位移情况时，推得铁磁圆板的横向磁弹性振动方程为

(11)

式中，Nr、Nθ、Nrθ为中面内力。

2 静载荷作用下圆板扰动微分方程

当铁磁圆板处于常磁场中时，即当Hn1和Hn2为恒定值时，由式(5)可得受到的磁体力为静载荷，即：

Fz=Q

(12)

并考虑轴对称情况，横向磁场中铁磁圆板的非线性振动方程可写为

设圆板在静载荷下产生微小静挠度w0，强迫振动挠度w1，总挠度为

w=w0+w1

则式(13)可以改写为

初始挠度满足

(15)

设满足周边夹支边界条件的位移函数为

(16)

对式(15)进行伽辽金积分并化简得到初挠度方程

(17)

其中，

求解得到：

(18)

设位移函数为

(19)

将式(15)代入到式(14)中，并进行伽辽金积分，得到扰动微分方程

B1q″+B2q′+B3q+B4q2+B5q3=B6Pz

(20)

3 多尺度法求解主共振问题

设激励力为Pz=P0cos(ωt)，对式(20)进行量纲归一化处理，考虑系统的弱非线性问题，引入小参数ε，得到

(21)

接下来应用多尺度法对具有初挠度扰动的系统主共振问题进行求解，分别考虑一阶近似求解和二阶近似求解两种情况。

3.1 一阶近似

取一阶近似解

(22)

其中，T0=τ，T1=ετ。

将式(22)代入式(21)中，令的ε0、ε1项系数相等，可得：

(23)

(24)

式(23)的通解为

(25)

(26)

(27)

令a′=γ′=0，得到稳态运动下常磁场中铁磁圆板主共振幅频响应方程

(28)

3.2 二阶近似

取二阶近似解

ε2q2(T0,T1,T2)

(29)

其中，T0=τ，T1=ετ，T2=ε2τ。

将式(29)代入式(21)中，并分别令ε的零次、一次、二次项系数相等，可得各阶近似线性偏微分方程组

(30)

(31)

(32)

式(30)的通解为

(33)

代入式(31)

(34)

式中,cc为各等式右侧各项共轭复数项之和。

消除久期项可得

(35)

式(35)代入式(34)，求解可得式(34)的特解为

(36)

将q0，q1代入式(32)中，并消除久期项

(37)

(38)

4 数值分析

针对横向交变磁场中受到横向简谐激励力作用的软铁磁马氏体钢制圆薄板进行数值分析。尺寸参数为：R=0.3 m，h=0.005 m(图2(a)和图3(a)除外)，物理参数取值如表1。

表1 圆薄板物理参数[21]

图2和图3分别绘制了一阶近似和二阶近似求解方法下铁磁圆板的幅频特性曲线图。曲线表明，振幅在共振区域(εσ≈0附近)显著增加，曲线存在向右偏移现象，呈现硬弹簧特性。且随着调谐值由负数逐渐增加为正数时，共振幅值由单值解变为多值解。由图2(a)和图3(a)可看出，随着板厚增加，共振区域逐渐变窄，且当下表面磁场强度为100 A/m时，一阶近似与二阶近似解得的振幅十分相近，但图3(a)中的曲线振幅稍大。由图2(b)和图3(b)可看出，磁场强度较小时图2(b)中的曲线没有变化，而图3(b)中曲线随着磁场强度增大，曲线向右偏移的角度变小，有向左偏移的趋势。出现这种现象的原因可见式(28)和式(38)，二次非线性项系数中含有静载荷项，利用一阶近似多尺度法求解时，幅频响应方程中不体现二次项，常磁场仅影响阻尼项和固有频率，因此磁场较小时共振曲线无变化；而二阶近似求解时，随着磁场强度增加，二次项系数增大，其非线性增大，因此曲线逐渐向左偏移。图2(c)和图3(c)中曲线表明，随着激励力幅值增大，共振区域逐渐拓宽，上支曲线和下支下半部分振幅增大，下支上半部分曲线振幅减小。

图2 一阶近似幅频特性曲线图

图3 二阶近似幅频特性曲线图

图4和图5分别绘制了一阶近似和二阶近似求解下的振幅-磁场强度特性曲线图。由各图中的曲线可以看出，振幅-磁场强度特性曲线关于磁场强度Hn2=0 A/m呈左右对称形式，且在磁场强度较小时便激发了共振，振幅较大。由图4看出，当调谐值较小或激励力幅值较大时，曲线为单值解；随着调谐值增加或激励力幅值减小，两腰侧曲线开始内缩，存在多值解，直至最后分离形成上部分封闭曲线。图5曲线呈牛角状，当调谐值较小、激励力幅值较大时曲线两腰向内微收，随着调谐值增加、激励力幅值减小，两腰侧曲线内缩更加明显，最后两部分曲线分离形成上部分封闭曲线，存在3个解。

通过对比图4和图5发现，当磁场强度较小时一阶与二阶近似共振振幅大小相近，而当磁场强度增加到250 A/m时，二阶近似振幅急剧减小，但由于一阶近似求解时不体现含有常磁场静载的二次非线性项，因此一阶近似振幅在Hn2=12 000 A/m左右时才急剧减小。综上所述，磁场强度较小时一阶近似与二阶近似计算结果相近，而磁场强度较大时，二阶近似计算结果更加准确。

图6和图7给出的是不同调谐值与不同磁场强度下一阶近似和二阶近似振幅-激励力幅值特性曲线图。

图4 一阶近似振幅-磁场强度特性曲线图

图5 二阶近似振幅-磁场强度特性曲线图

图6 一阶近似振幅-激励力幅值特性曲线图

图7 二阶近似振幅-激励力幅值特性曲线图

图中曲线表明，当激励力幅值较小时便可以激发系统的主共振现象，且出现多值解，之后振幅随着激励力幅值的增大由多值解变为单值解，且单值解缓慢增加。曲线向左偏移，呈现软弹簧特性。

比较图6(a)和图7(a)看出，在Hn2=200 A/m时，图7(a)共振幅值大于图6(a)的共振幅值，随着调谐参数增大，上支曲线与下支上半部分曲线共振振幅增大，而下支下半部分曲线振幅减小。由图6(b)和图7(b)相比较可看出，图6(b)中在磁场强度数值较小时，曲线没有变化；图7(b)中上支曲线与下支上半部分曲线共振振幅随着磁场强度的增加而增加。

图8和图9通过提取共振曲线出现多值解的临界点绘制了分岔点变化图。其中：图8(a)和图9(a)分别提取了图2(a)和图3(a)中的多值解临界点，绘制出板厚-调谐参数的共振分岔点变化曲线，曲线呈向右下凹形非线性变化，随着板厚的减小，相应的调谐值增大而出现共振分岔现象；图8(b)和图9(b)分别提取了图6(b)和图7(b)中的多值解临界点，绘制出磁场强度-激励力幅值的共振分岔点变化曲线，曲线呈向右上非线性变化趋势，随着磁场强度的增大，相应的激励力幅值增大而出现共振分岔现象，且在激励力幅值较小时，曲线斜率非常大；图8(c)和图9(c)分别提取了图4(a)和图5(a)中的多值解临界点，绘制出磁场强度-调谐值的共振分岔点变化曲线，曲线呈向右下拱形非线性变化走势，随着磁场强度的减小，相应的调谐值增大而出现共振分岔现象。

图8 一阶近似求解分岔点

图9 二阶近似求解分岔点

图10和图11绘制了两种求解方法下的不同参量三维曲线变化图。由图10(a)和图11(a)看出，振幅随调谐值变化时，在共振区域振幅增加，且存在跳跃性，激励力幅值变大时共振曲线整体走势不变但共振区域拓宽。由图10(b)可看出，一阶近似下共振曲线在磁场强度较小时为分离的上下两支曲线，当磁场强度增大后，共振曲线变成一条曲线且最大振幅减小。由图11(b)可看出，在二阶近似下，共振曲线随着磁场强度的增加，逐渐向另一侧偏移，系统由硬弹簧特性变成软弹簧特性。由图10(c)和图11(c)中三维曲线发现，激励力幅值较小时，振幅-磁场强度曲线为封闭曲线与平滑曲线两部分，随着激励力幅值增长，两部分曲线逐渐靠近，最后合并成一条曲线。