基于多重分形的离心压缩机出口动态压力非线性特征研究及其在喘振识别中的应用
2021-01-16刘雁,高宽,何浩,马凯
刘 雁, 高 宽, 何 浩, 马 凯
(西北工业大学 机电学院,西安 710072)
离心压缩机在运行过程中,若流量减小到一定程度时,将发生非正常工况下的流动失稳,即喘振。喘振作为压缩机的一种固有特性,在对压缩机内部造成巨大冲击的同时也使整个机组产生强烈振动,可使压缩机转子和静子受交变力作用断裂,从而引起叶片飞出,甚至发生机毁人亡的事故[1]。因此,寻找一种准确快速的喘振识别及预测方法是保证压缩机高效运行的必要条件。
近年来,研究人员分别从喘振发生机理、分析预测及防喘振控制等方面进行了研究,旨在避免压缩机工作时喘振的发生。在喘振机理研究方面,其中一项研究热点就是压缩机喘振的模型研究。目前,国内外较为广泛用于研究的模型是Greitzer模型及其衍生的喘振模型,通过研究其结构参数的改变对系统压比和流量变化的影响,分析系统的工作状态,以期达到避免喘振的目的[2-5]。在喘振分析和预测方面,目前采用较多的方法是通过测试压缩机的出口压力和压缩机喉部压差判断系统是否工作在安全工作区。
虽然离心压缩机系统设置了安全工作区,可以使压缩机远离喘振区,达到离心压缩机防喘振的效果,但由于防喘振线的设置需要考虑安全裕度,相应的就要牺牲压缩机的工作效率。近年来,研究人员发现,当压缩机发生喘振之前,由于管网中积蓄了高压气体,在压缩机的叶道中会出现气流的严重分离,即旋转失速。而旋转失速作为离心压缩机产生喘振的前奏,可以在压缩机的出口管道中的气体动态压力上体现出来[6]。随着对离心压缩机喘振机理研究的深入,研究人员发现在压缩机的出、入口及叶轮处的压力信号属于非线性信号。因此,一些非线性动力学的分析方法如小波图像处理技术、神经网络和单重分形等被引入并应用于压缩机的出、入口的气体动态压力测试,目的是实现压缩机的喘振预测[7-9]。而在防喘振控制方面,目前也较多的采用如模糊控制、神经网络可变控制以及非线性主动控制等非线性控制方法实现[10-11]。
分形理论作为分析非线性系统中信号的一类重要方法,广泛地应用于湍流、地球科学、遗传学、生命科学和金融领域[12]。而离心压缩机出口动态压力信号作为一种典型的非线性信号,可以采用分形理论对其进行分析。在此动机下,我们采用了单重分形理论对其进行分析,分析出系统在不同工作状态下的动态压力变化的自相关特性。随着研究的深入,我们发现,当系统从稳态进入到喘振状态,其多重分形特性表现得更加明显。基于此背景,我们以800 kW离心压缩机系统在不同工况下的出口动态压力特征为分析对象,从非线性角度分析其多重分形特征,研究其精细结构的动力学特征,以期达到早期识别和预测喘振的目的,为压缩机喘振的主动控制奠定基础。
1 多重分形
简单地说,多重分形即为分形对象的分解,分解后每部分均有自己的分形维数。通过多重分形可以描述分形体不同层次的特征,即其局部奇异特性。
1.1 多重分形及其谱参数
假定一单位区间具有单位质量,将其分成若干子区间,每个区间长度为δ,同时为第k个子区间分配一个非负的包含时间点t0的序列μk(k≥1),则定义μk在时间点t0处的奇异性指数α(t0)为
(1)
奇异性指数α(t)也称作Hǒlder指数,在分形理论中表征分形体某小区域的分维,又称为局部分维,其值的大小可以反映小区域生长几率的大小。
对于一个时间序列,如果式(1)中的极限不存在,则表示序列在t0处的奇异性指数没有定义;如果α(t)为一常数,则说明该序列的奇异性可以仅用一个全局尺度指数来表征,这种分形特征就是单重分形特征;如果α(t)随时间t的变化而变化,即其尺度行为特征与时间有关,则表示该序列具有多重分形特性。与单重分形相比,多重分形的概念推广和拓展了人们对尺度行为的理解和认识,与时间相关的尺度特性能够反映出局部时间范围内的不规则现象[13]。
多重分形可用于表示分形体中小区域的分维,如果小区域的数目很大,α(t)则将单重分形的分形指数(又称为Hurst参数)扩充到多值,这就需要知道α(t)取不同值的概率,才能分析时间序列的特征。于是,得到了一个由不同α(t)组成的无穷序列构成的谱f(α)。f(α)的物理意义是表示相同α值子集的分形维数,即表示α(t)出现的概率,称为多重分形频谱(简称多重分形谱)。f(α)的取值应在[0,1]之间,通常是上凸形状(∩),也可以将多重分形谱理解为指数α(t)的概率分布(即密度)[14]。
1.2 多重分形谱物理量之间的关系
为了计算多重分形谱,通常采用盒子计数法,即把采样区间内的时间序列作为一维点集,用“盒子”进行覆盖。用度量为ε的“盒子”,将时间序列分为N个小区间。其中,ε趋近于0。将时间序列在该小区间的概率定义为Pi(ε)整个序列内奇异性指数相同的小区间个数定义为N(ε),则Pi(ε)和N(ε)的关系式定义为
Pi(ε)∝εα
(2)
N(ε)∝ε-f(α)
(3)
其中,α可以反映时间序列在不同划分尺寸ε下,物理量分布概率Pi(ε)随ε变化的各区间的性质,α越大,子集的概率越小(因为ε<1)。
统计物理给出了规则和不规则多重分形谱的计算方法。首先,定义一个配分函数
(4)
式(4)中,q称为权重因子,多重分形谱通过不同q的取值将分形体分成具有不同层次的区域来研究[14-15]。
若配分函数收敛,则等式
χq(ε)=ετ(q)
(5)
成立,即可以得到
τ(q)=lnχq(ε)/ln(ε)
(6)
其中,τ(q)称为结构函数。
设N(Pi)是概率为Pi(ε)的小区间的数目,则有
(7)
将式(2)、(3)代入式(7),并根据式(6)可以得出多重分形谱f(α)和奇异性指数α
f(α)=q·α-τ(q)
(8)
(9)
在分形结构中,单重分形可以看作是多重分形的特殊情况。当系统具有单重分形特征时,α(t)为一常数,用Hurst参数表示,f(α)为1。此时,式(8)可以变换为
1=q·H(q)-τ(q)
(10)
式(10)中,H(q)是Hurst参数,为一常数。此时,τ(q)为H的线性函数[16]。对于具有单重分形特征的时间序列,由于H(q)是常数,τ(q)和q满足线性关系;而当序列具有多重分形特征时,τ(q)则表现出非线性特性。因此,结构函数的形状呈现凸形是序列具有多重分形特性的典型标志。
1.3 多重分形谱与离心压缩机出口动态压力
奇异性指数α(t)的大小取决于离心压缩机系统在其动态行为中的信息,不同的α(t)值表示了系统在不同层次的奇异性程度。其中,多重分形谱参数αmin和αmax分别是最大和最小概率分布Pi(ε)的奇异性指数。因此,多重分形谱f(α)可以度量离心压缩机出口动态压力分形结构的复杂程度。定义多重分形谱的宽度
Δα=αmax-αmin
(11)
Δα的大小反应出口动态压力概率分布的均匀度,可以表征在标度不变的情况下,所分析时段内出口动态压力分布的均匀程度,即出口动态压力的幅度变化。谱宽度Δα越大表示出口动态压力分布越不均匀,波动越剧烈。Δα=0则对应完全均匀分布的状况,即当压力无任何波动时,多重分形谱将退化成二维空间中的一个点,此时就是均匀分形。
f(αmin)和f(αmax)分别表示最大值、最小值概率子集Pi(ε)的分形维数,可以分别描述出口动态压力最大值和最小值出现的次数。定义多重分形谱参数Δf(α)
Δf(α)=f(αmin)-f(αmax)
(12)
Δf(α)能够描述最大、最小概率的数目之比[17]。若多重分形谱的左端低于右端,图形向右钩,即Δf(α)<0,表示出口动态压力序列在这段时间内处于最小值的概率较大;若多重分形谱左端高于右端,图形向左钩,即Δf(α)>0,表示出口动态压力序列在这段时间内的幅值处于最高值的概率较大。
2 出口动态压力采集及频谱分析
2.1 采集系统
图1为用于分析离心压缩机工作状态的采集系统,其中离心压缩机的叶轮叶片数为16片,叶轮的额定转速为9 620 r/min,马赫数为0.6,由一台800 kW的直流电动机拖动。处于室温状态的大气,首先经过空气过滤器进入工作管路,在风室中等待压缩,当压缩机工作时进入离心压缩机。压缩后的气体通过出口管道及直径分别为250 mm和100 mm的两个电动防喘振阀,进入排气消声器,最终排入大气。
本文所分析的数据由动态压力采集模块完成,数据为800 kW离心压缩机系统在不同工况下的出口管道的动态压力。动态数据采集系统采用美国Crystal Instruments公司的动态信号分析仪CoCo-80,采样频率为20.48 kHz。传感器选用美国Kulite公司的动态压力传感器。
系统通过调节大防喘振阀和小防喘振阀的开度实现对出口压力的控制,随着防喘振阀的开度逐渐减小,系统逐渐由稳定状态进入喘振状态。整个实验过程为635.5 s,本文选取其中180~330 s共150 s的出口动态压力数据进行分析,将第180 s定义为时间起点。这段时间的数据包含了系统由稳态过渡到喘振的过程。
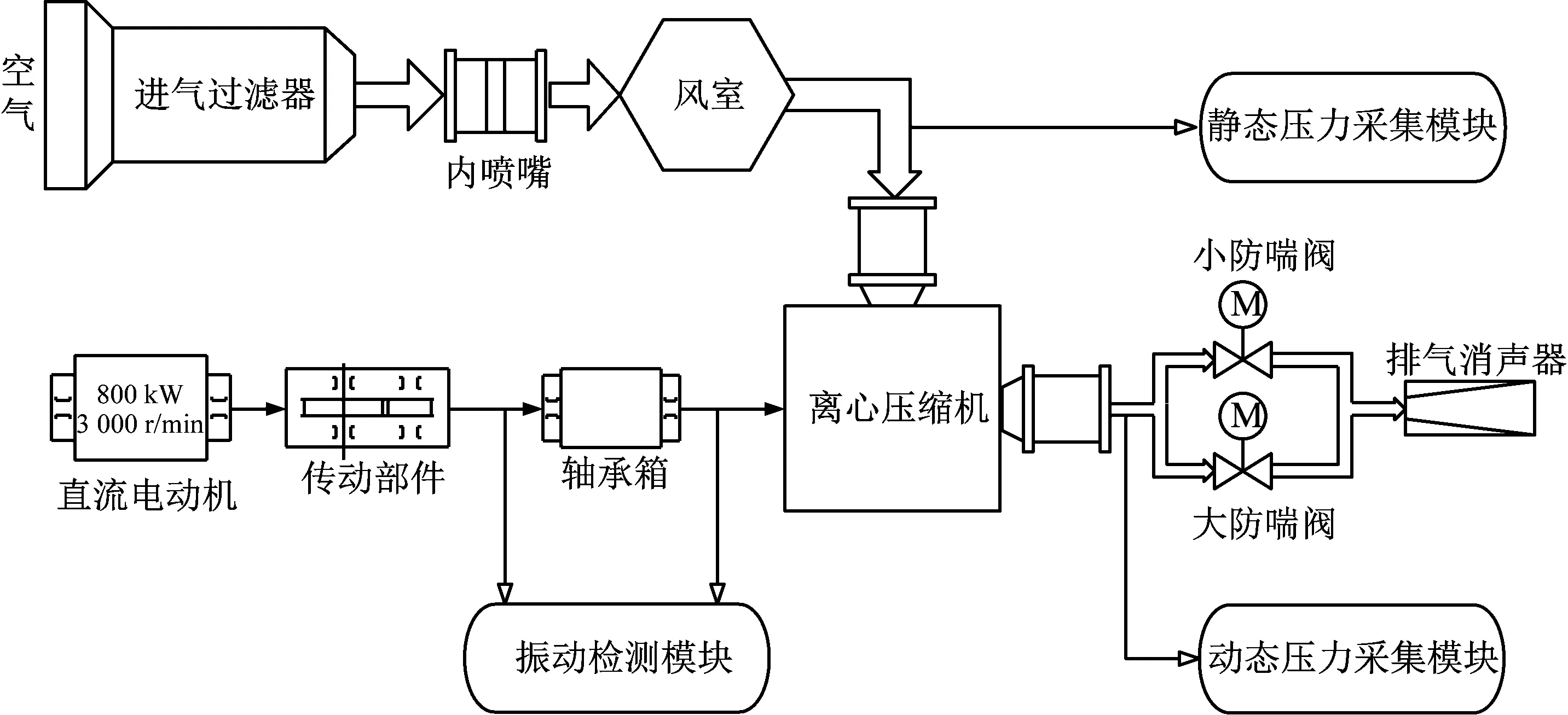
图1 采集系统
2.2 离心压缩机出口动态压力的波形与频谱
图2为离心压缩机的防喘振阀由打开到关闭时,离心压缩机出口动态压力的变化波形。可以看出,系统经历了稳态、过渡过程,最终进入喘振状态。在防喘振阀打开时,出口动态压力处于稳态阶段,如图2中的0~85 s时的状态,此时出口动态压力幅值较小,波形表现出随机特性。随着防喘振阀开度的减小,压缩机经过过渡过程进入喘振状态,出口动态压力幅值逐渐增大,如图2中的85~96 s。随着失稳状态的加深,系统进入喘振状态,出口波形开始表现出规律振动,波动周期明显变长,如图2中的96~150 s。
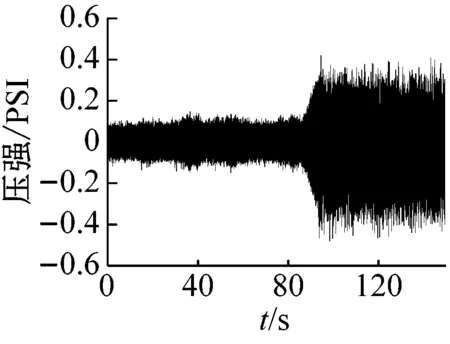
(a) 0~150 s
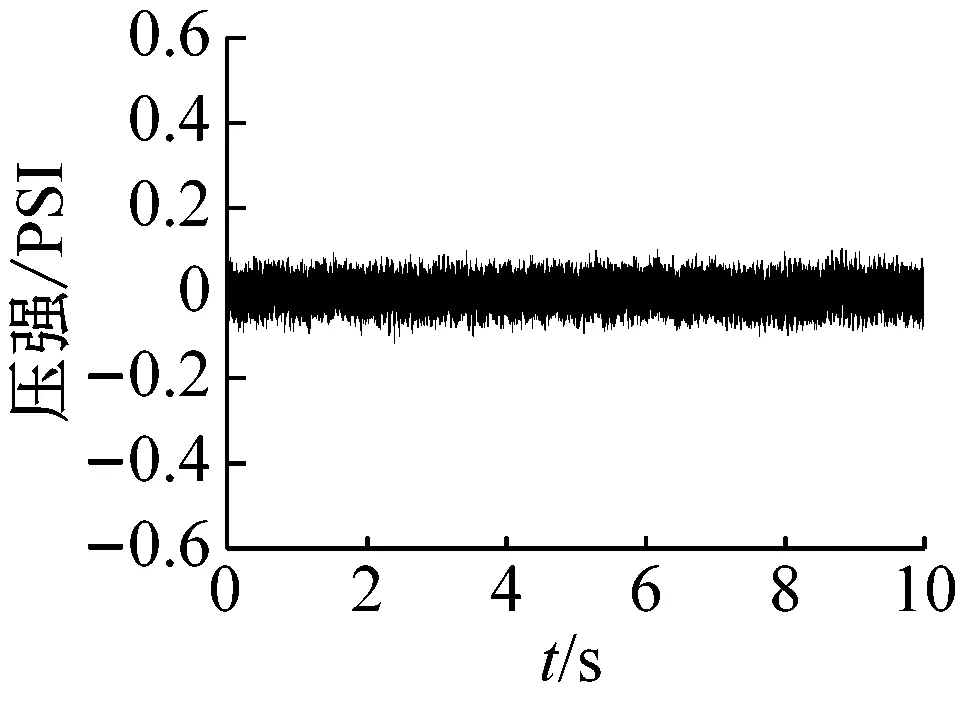
(b) 稳态时(0~10 s)
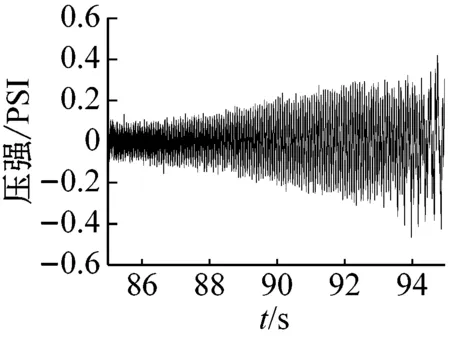
(c) 过渡过程时(85~95 s)
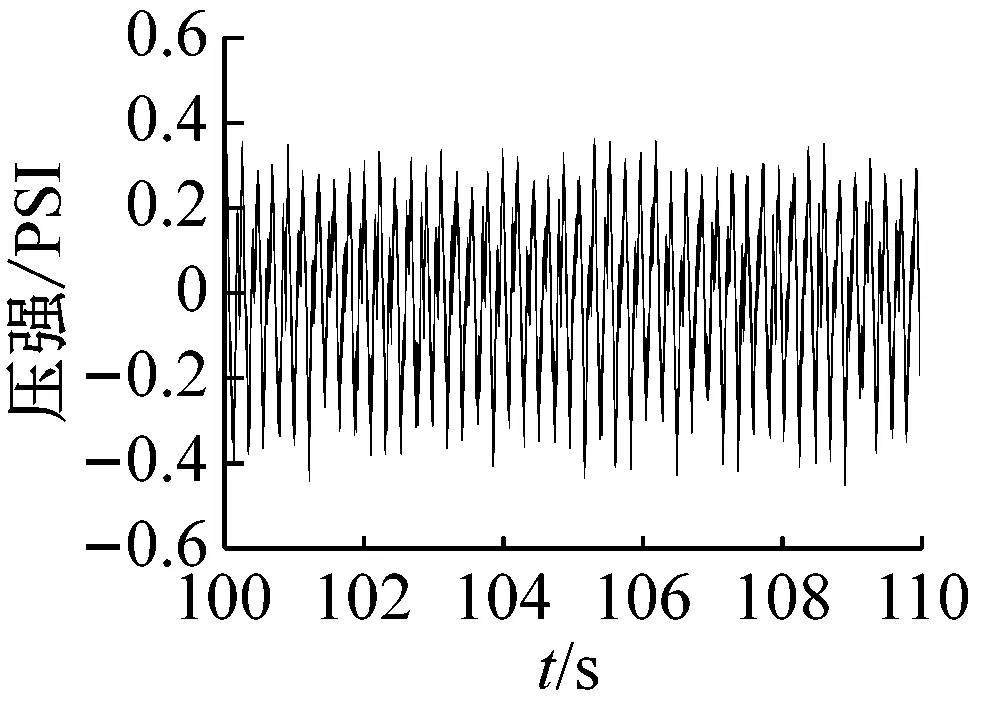
(d) 喘振时 (100~110 s)
图3为这三种工作状态时部分时段的频谱图,从图3可以看出,压缩机在稳态时出口动态压力的频谱较为分散,而随着喘振的加深,频谱越来越向低频处集中。进一步,从图3(c)可以看出,离心压缩机喘振时的频谱主要集中在0~0.2 Hz,能量高度集中,对系统的破坏力很强,极易发生事故。
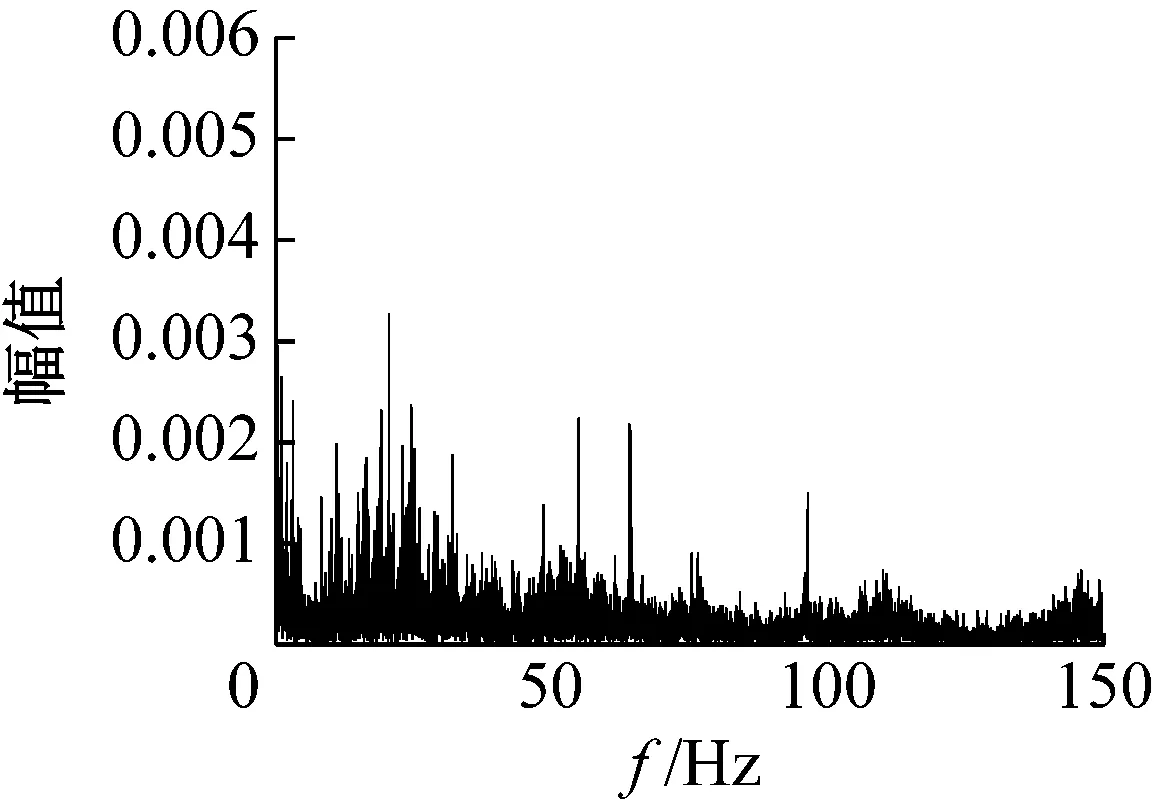
(a) 稳态时(0~10 s)
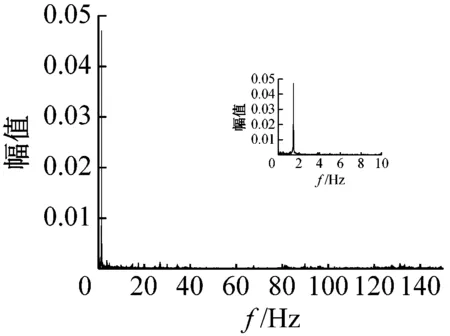
(b) 过渡过程时(85~95 s)
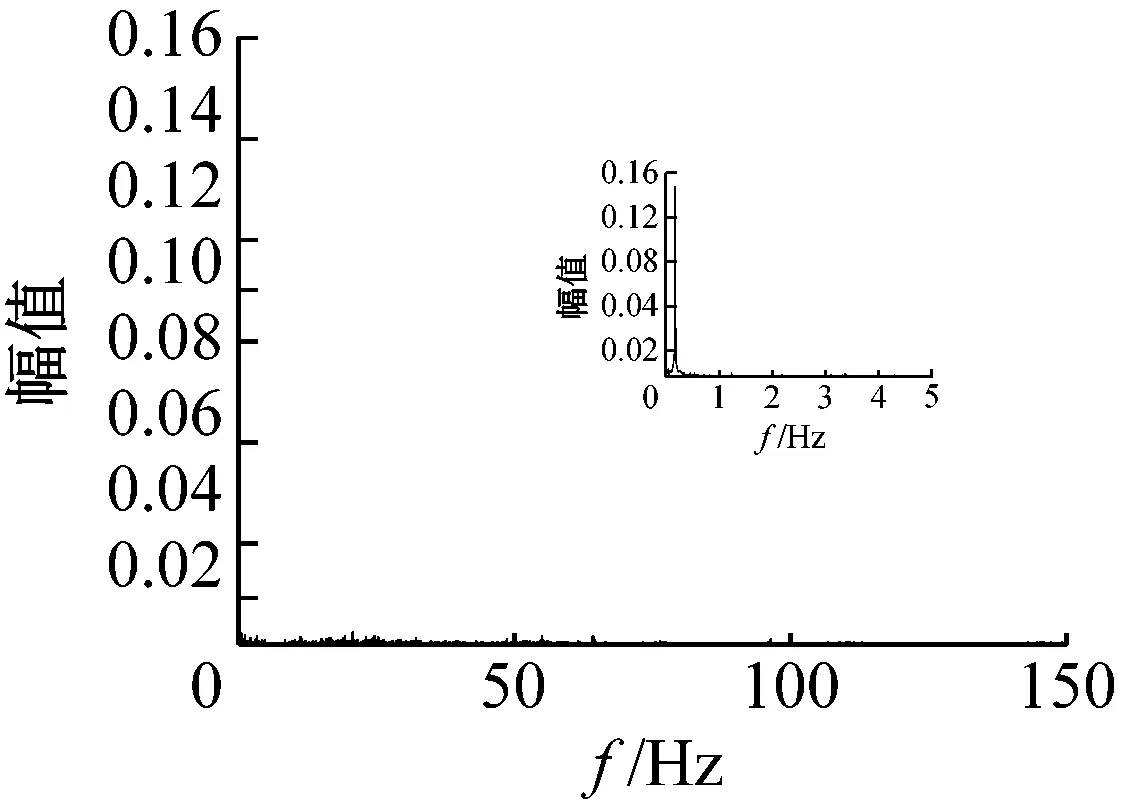
(c) 喘振时(100~110 s)
3 离心压缩机出口动态压力的多重分形特征
3.1 离心压缩机出口动态压力的结构函数
图4所示为离心压缩机出口动态压力的结构函数τ(q)的随权重因子q的变化曲线。这里选择离心压缩机在稳态、过渡过程和喘振三种状态的时段,每个时段选取5 s,以1 s为分析单元进行分析。从图4可以看出,在稳态时,结构函数随权重因子q的变化曲线十分平直,当系统进入非稳定状态时,曲线出现曲度,而随着系统经过过渡过程进入喘振状态,曲线的曲度加深。说明系统在稳态时的单重分形特征明显高于非稳态。系统从过渡过程进入喘振状态,系统的多重分形特征相应地变得十分明显。因此,我们进一步从多重分形的角度研究系统的非线性特征。
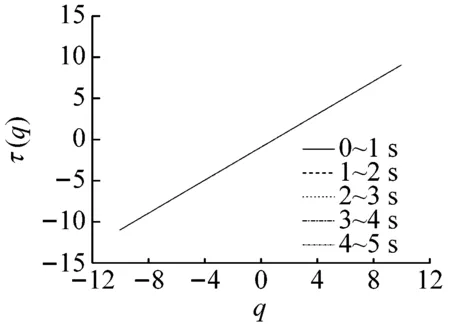
(a) 0~5 s
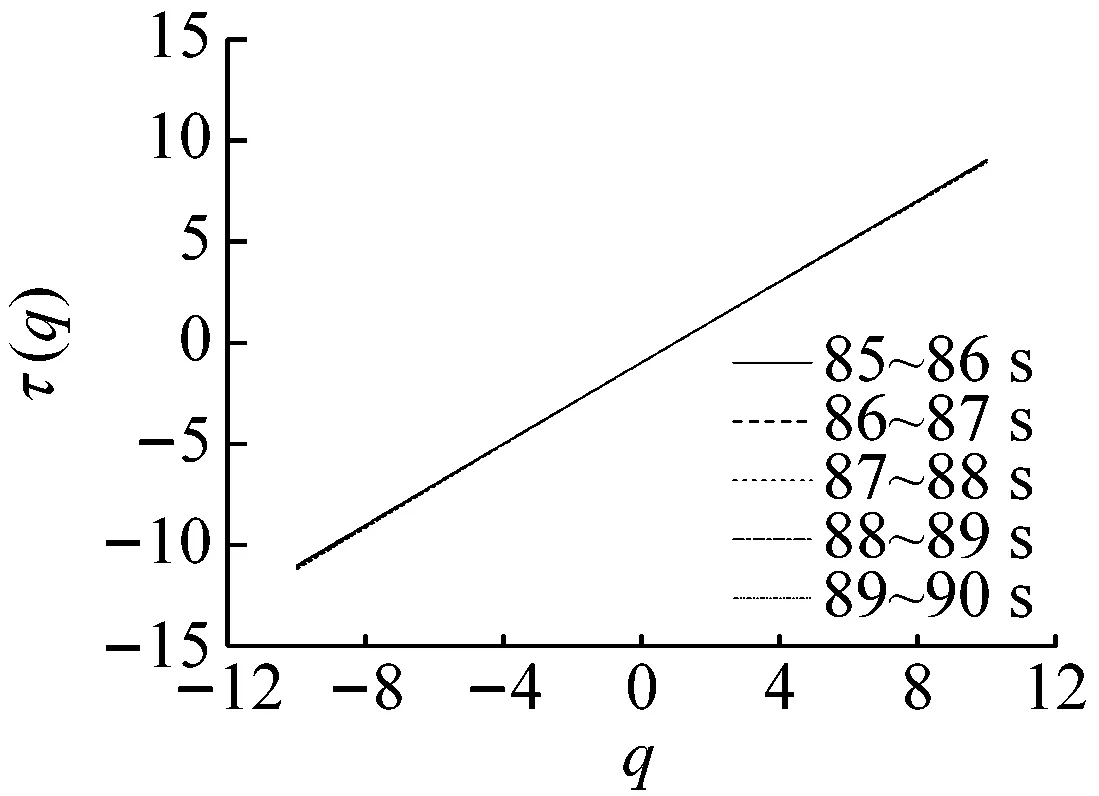
(b) 85~90 s
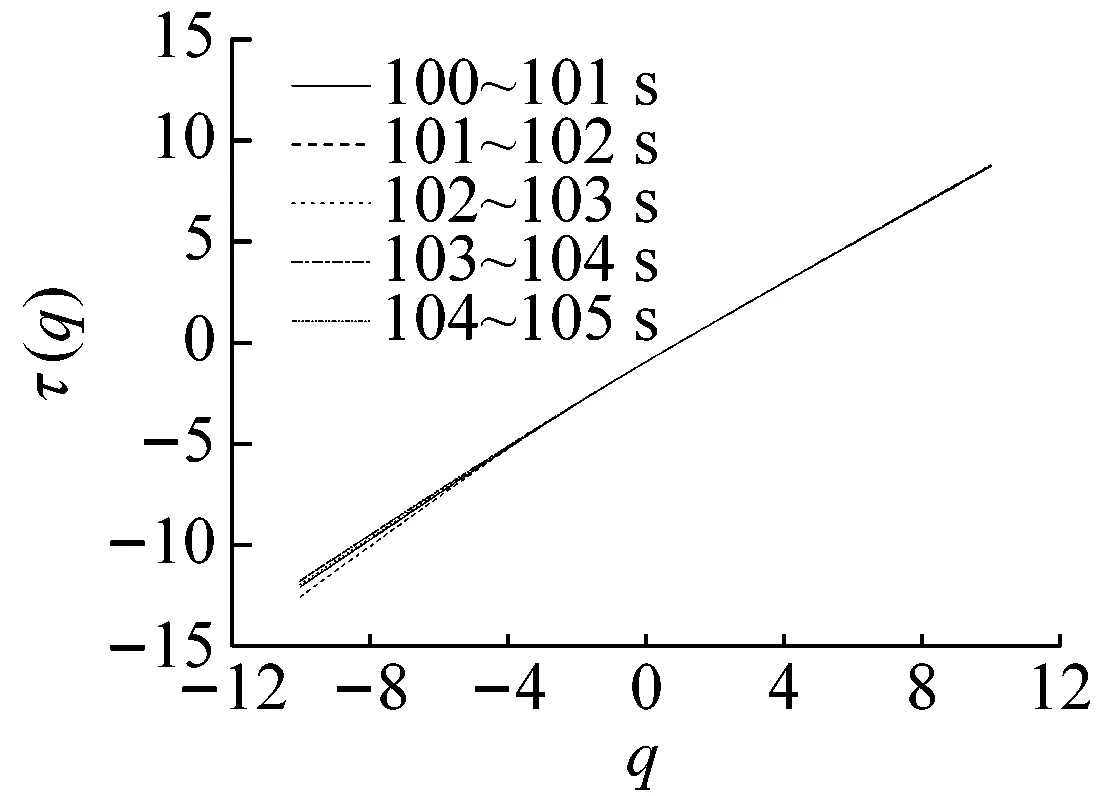
(c) 100~105 s
3.2 离心压缩机出口动态压力的多重分形谱
同样选取稳态、过渡过程和喘振三种状态,6个时段分析,每个时段选取5 s,以1 s为分析单元画出多重分形谱如图5所示。从图5可以看出,几乎所有时段的多重分形谱图都表现出向左钩的图形特征,即Δf(α)>0,表示这些时段出现最大值的概率大于出现最小值的概率。在稳态时,Δα很小,Δf(α)也较小,表明在此阶段离心压缩机的出口动态压力分布较均匀,系统发生喘振的几率较小。而随着系统由稳态经过过渡过程进入到喘振状态,Δα和Δf(α)都在增大,说明系统动态压力分布变得不均匀。而且在过渡过程时,Δα和Δf(α)的变化量都较大,说明此阶段系统的出口动态压力的分布十分不均匀,而且最大值、最小值出现的概率也不稳定。系统处于不稳定状态,极易引发失稳现象,从而发生喘振。
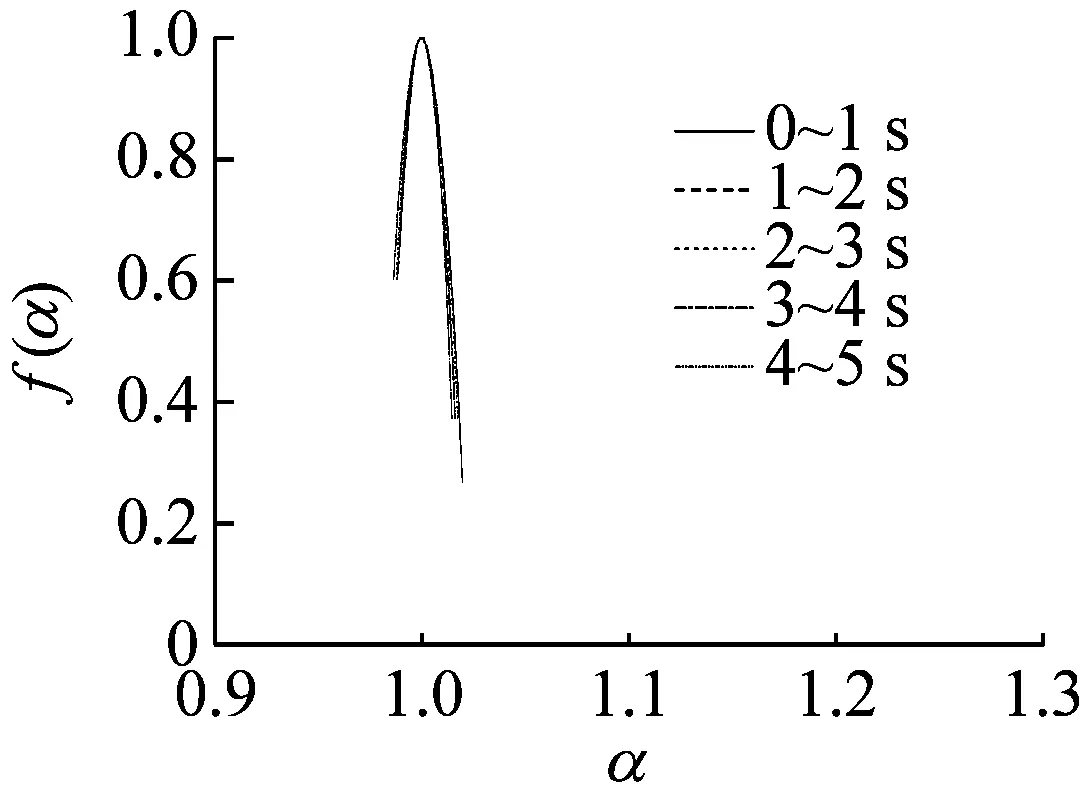
(a) 0~5 s
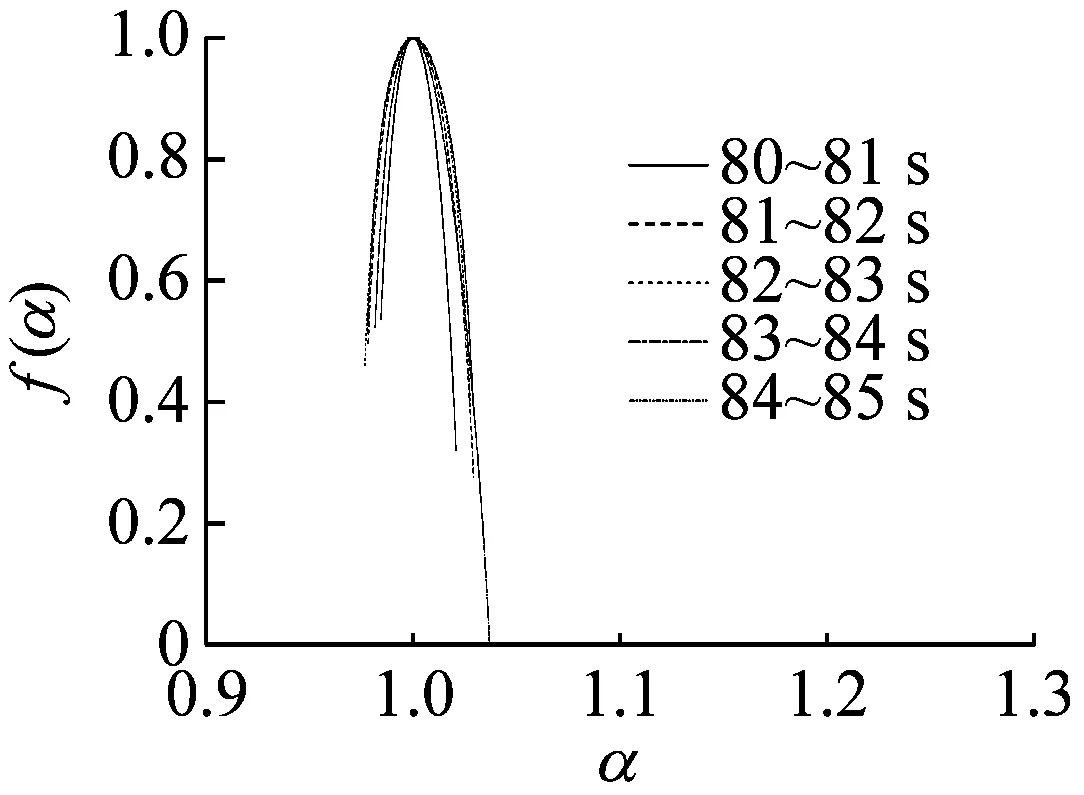
(b) 80~85 s
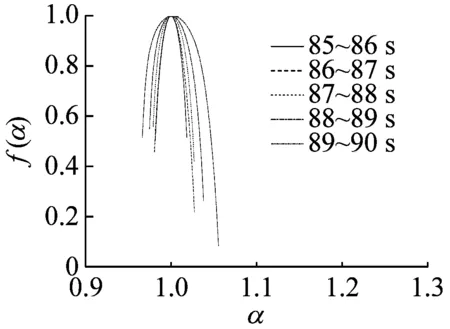
(c) 85~90 s
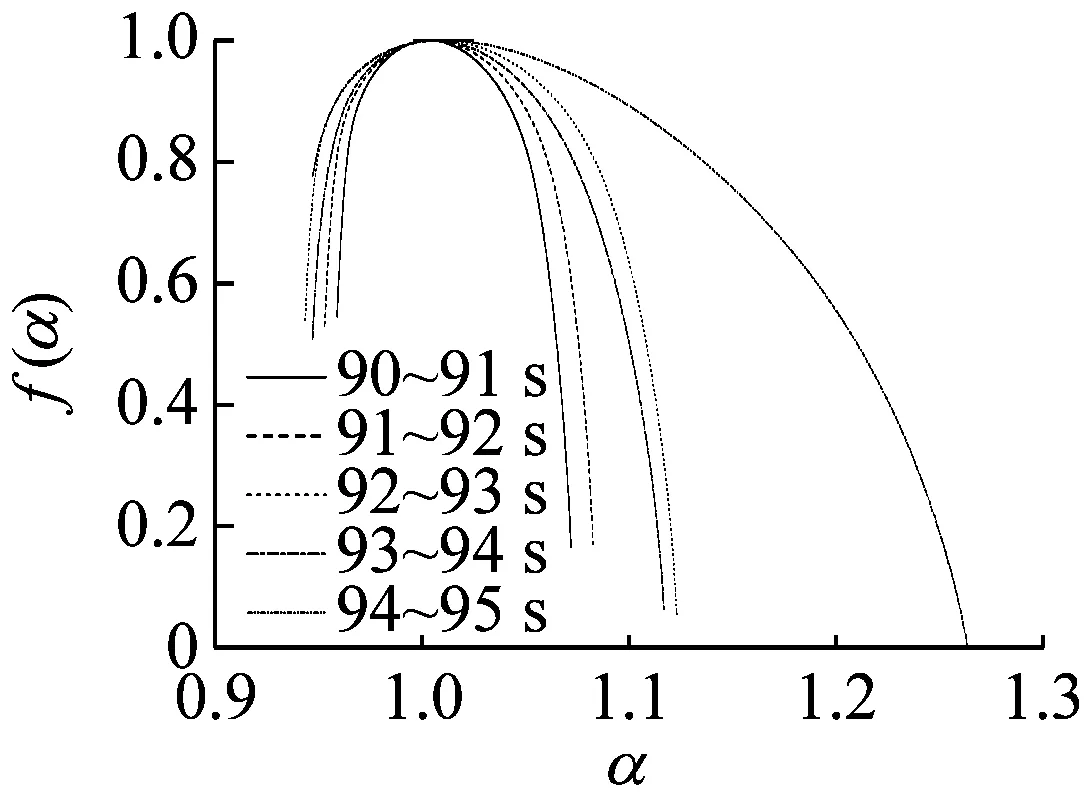
(d) 90~95 s
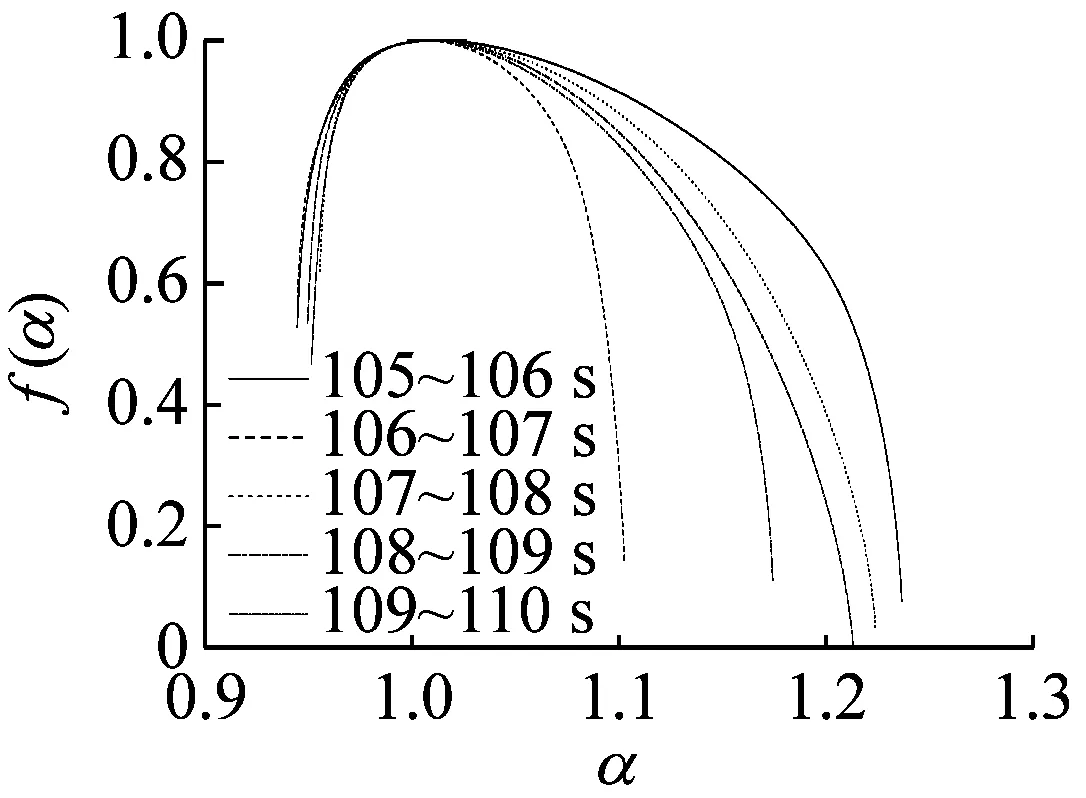
(e) 105~110 s
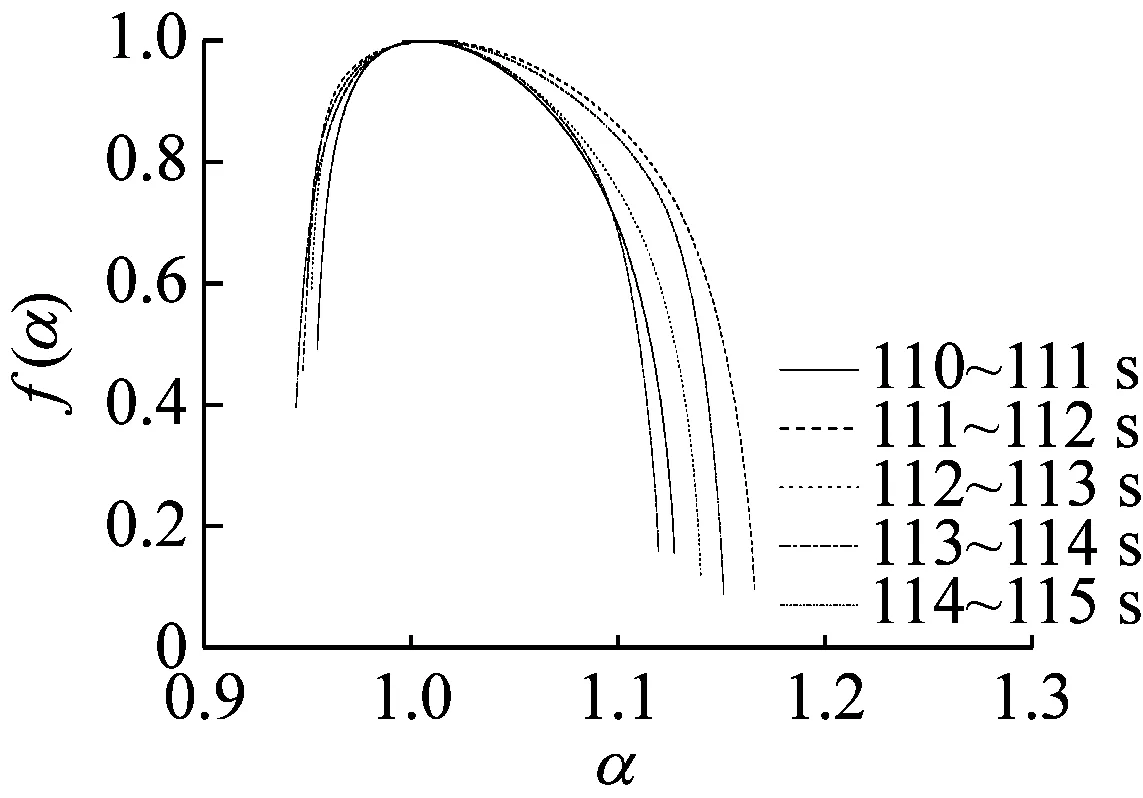
(f) 110~115 s
3.3 权重因子的选择与多重分形谱
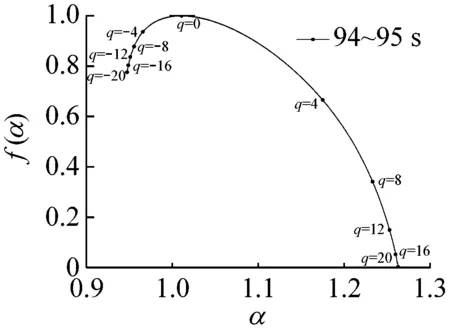
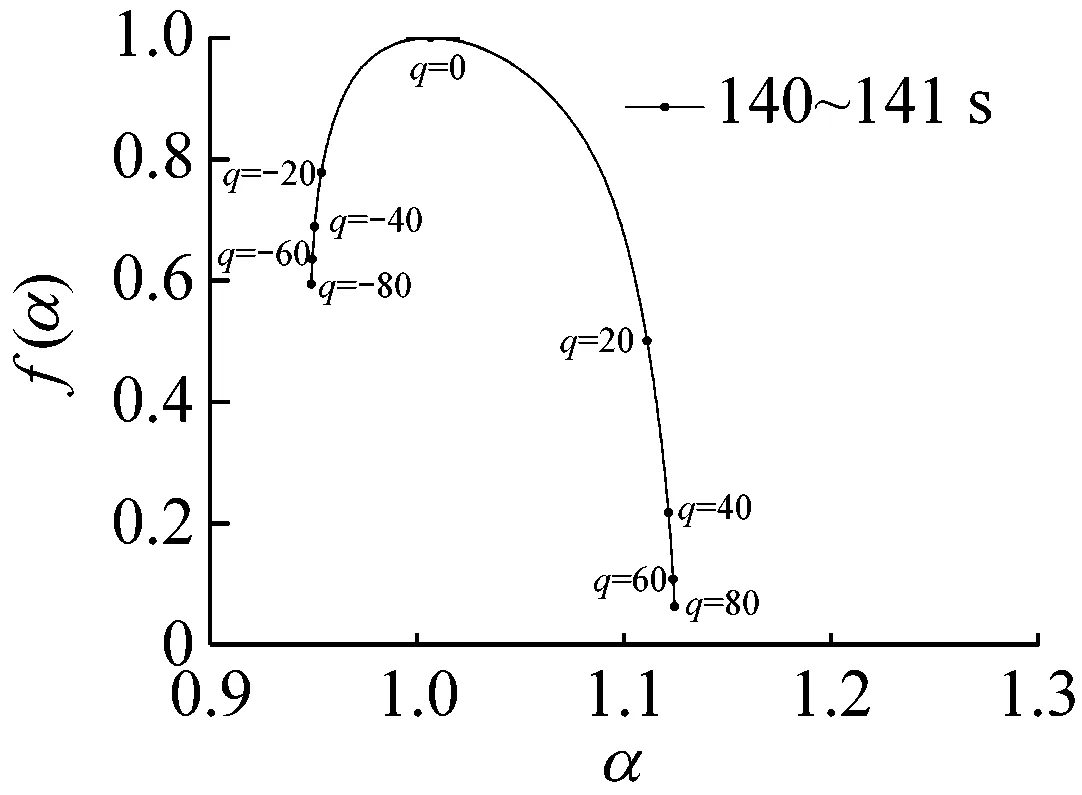
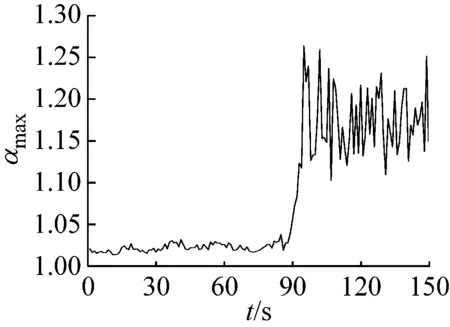
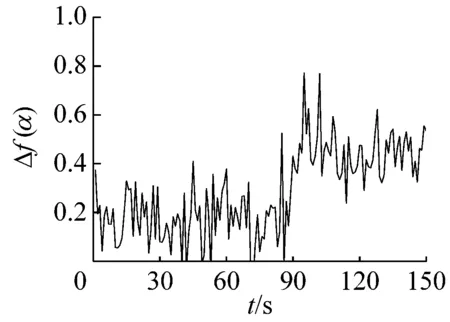
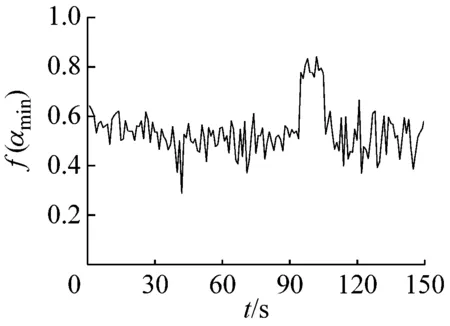
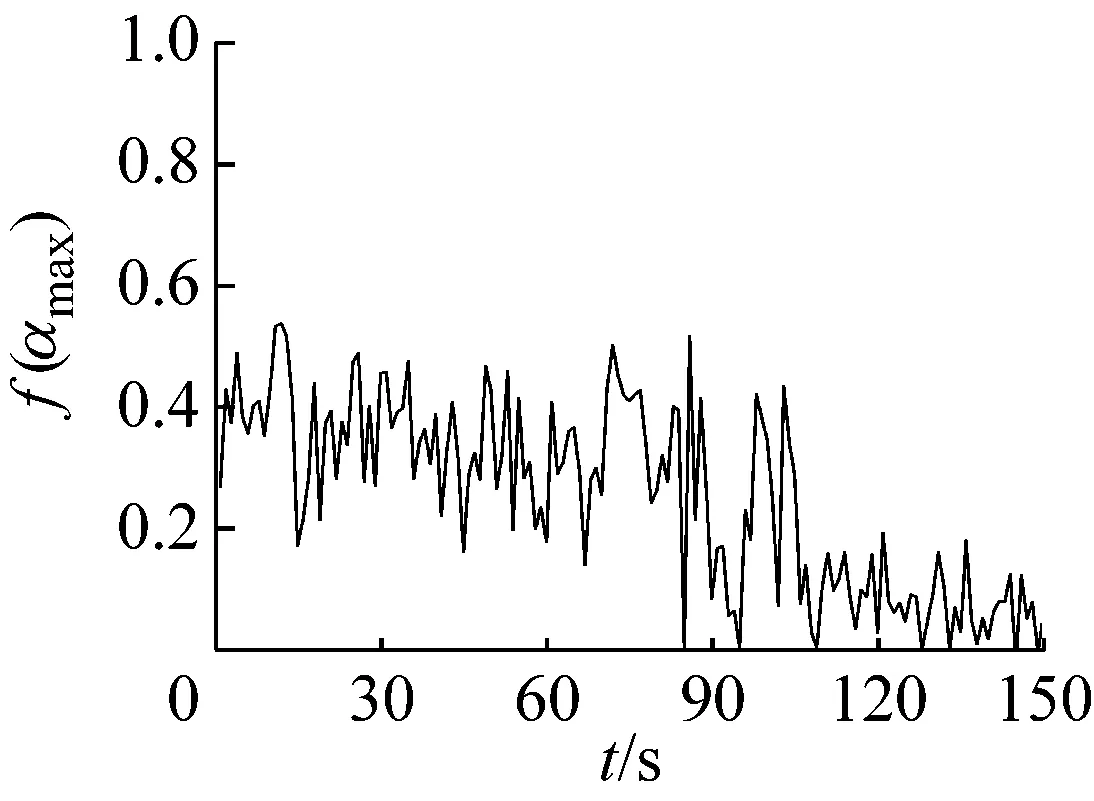
多重分形是通过不同q的取值将分形体分成具有不同层次的区域进行研究的。理论上q值的范围越大越好(-∞ 图6所示为系统在稳态、过渡过程和喘振三种状态中各选取1 s画出的权重因子q与多重分形谱的关系曲线。其中,40~41 s和140~141 s权重因子的范围为-80 (13) 其中,fmax为1。由于对于同一个|q|有2个k值,在实际计算时可以选择较大的值,然后通过设定k的阈值,如不超过0.1%,即可选取q的范围。按照这种选择方法,同时结合计算机运算工作量,在保证不发生溢出错误的情况下,0~94 s和106~150 s的压力序列选取|q|max=80,而94~106 s的压力序列选取|q|max=20。即可以保证全面分析动态压力的概率分布。 (a) 40~41 s (b) 94~95 s (c) 140~141 s (a) 40~41 s (b) 94~95 s (c) 140~141 s (a) 40~41 s (b) 94~95 s (c) 140~141 s 图9为离心压缩机出口动态压力的多重分形谱参数随时间的变化曲线,从图中可以看出离心压缩机从稳态到喘振,多重分形谱的各参数都发生了明显的变化。通过研究各参数的变化规律,得出以下结论: (1) 在0~85 s时,Δα接近于零,αmin最大而αmax最小,表明在此阶段系统出口动态压力分布均匀,波动较为平稳,出现喘振的几率较小。 (2) 在85~96 s时,αmax的值迅速增大,而αmin的值则迅速减小。这使得Δα迅速增加,系统出口动态压力的分布变得不均匀。f(αmax)在这一阶段波动的十分剧烈,表明压力波动出现最小值的概率变化较大,而f(αmin)波动变化不明显,表明压力波动出现最大值的概率变化不大。Δf(α)在此阶段出现了波动向上的变化趋势,表明压力波动出现最大值的概率与最小值的概率相比在增加,系统开始变得不稳定。 (3) 在96~150 s时,离心压缩机处于喘振状态,此阶段Δα的宽度远高于稳态时,表明压缩机的出口动态压力的分布不均匀,压力波动较为剧烈。多重分形谱参数在喘振阶段多处于较大的波动状态,表明系统的工作状态不稳定。与稳定状态相比,f(αmax)在这一阶段的值小于稳态时的值,表示此阶段出现最小值的概率小于稳态时的概率。f(αmin)在喘振阶段的波动和稳态时的波动量相比变化不大,即出现最大值的概率和在稳态时相当。因此,Δf(α)总体值也较大,表明出现最大值的概率与出现最小值的概率比值在增加。但是,f(αmin)在喘振初期出现了短暂的峰值平台,表明此时段出现最大值的概率最大,而且Δf(α)的峰值也出现在此短暂的时段,即出现最大值的概率与最小值的概率比值的最大值,表明此时段为出口动态压力波动最剧烈的时段。 进一步分析0~150 s的多重分形谱参数的变化规律。可以看出,所有多重分形谱参数在离心压缩机的过渡状态均出现了突变特征。其中,Δα、αmax和αmin在喘振时的波动量远大于稳态时的波动量,系统压力分布的不均匀程度较大。对于参数Δf(α)、f(αmax)和f(αmin)来说,在喘振时出现最小值的概率有所下降,而且在喘振初期,参数Δf(α)和f(αmin)出现了明显的高峰平台和峰值特征。因此,这几个参数可以进一步用于离心压缩机的初始喘振的预测。 (a) Δα (b) αmin (c) αmax (d) Δf(α) (e) f(αmin) (f) f(αmax) 以800 kW离心压缩机不同工作状态下的出口动态压力为研究对象,选取包含稳态、过渡过程和喘振状态150 s的数据进行分析,从多重分形的角度对其分形特征进行研究。离心压缩机出口动态压力结构函数的曲线在稳态时表现出线性特征,而在非稳态时表现出多重分形特征。表明离心压缩机出口动态压力的多重分形谱与离心压缩机的工作状态存在较为明显的关联关系。多重分形谱特征的分析结果显示,多重分形谱图在稳态时最窄,而经过过渡过程进入喘振,宽度明显增加,动态压力分布不均匀,并且在过渡过程时谱宽度的变化量较大,极易发生喘振。出口动态压力的多重分形谱参数在离心压缩机的过渡状态均出现了突变特征,尤其是Δα、αmin、αmax出现了明显的波动,而且这些参数在喘振时的波动量远大于稳态时的波动量。因此,可以采用这些参数判断系统进入过渡过程状态。而且,参数f(αmin)和Δf(α)在喘振初期也出现了明显的局部特征,两个参数可以用于判断系统是否进入喘振。因此,可以采用出口动态压力的多重分形谱参数实现离心压缩机初期喘振的识别和预测,并为进一步完成离心压缩机喘振的主动控制奠定基础。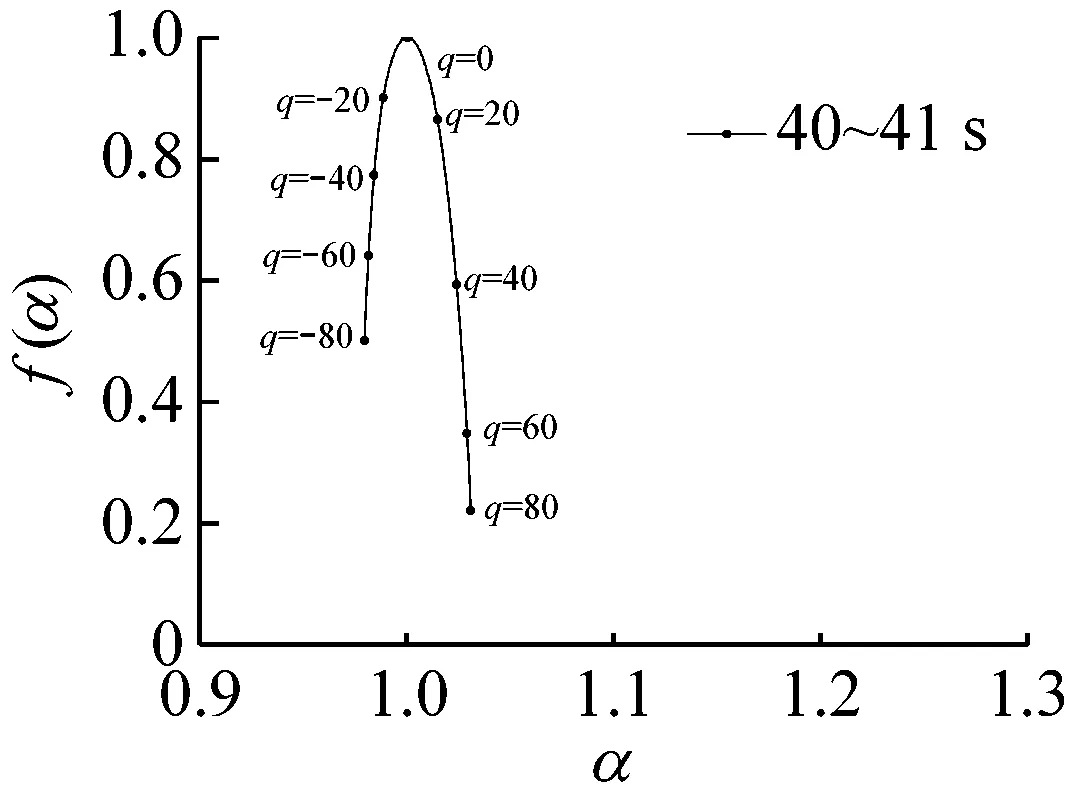
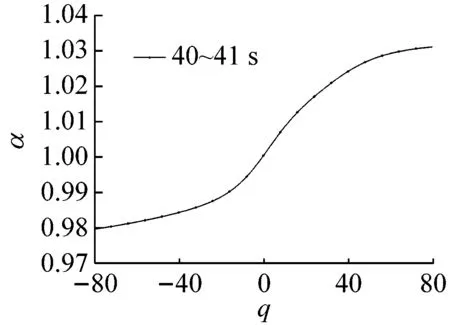
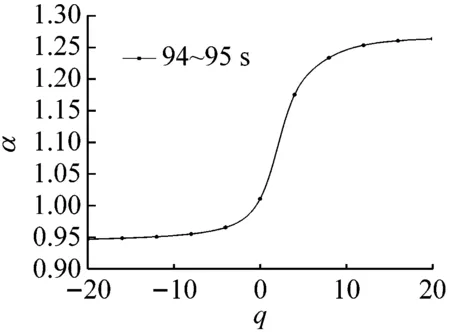
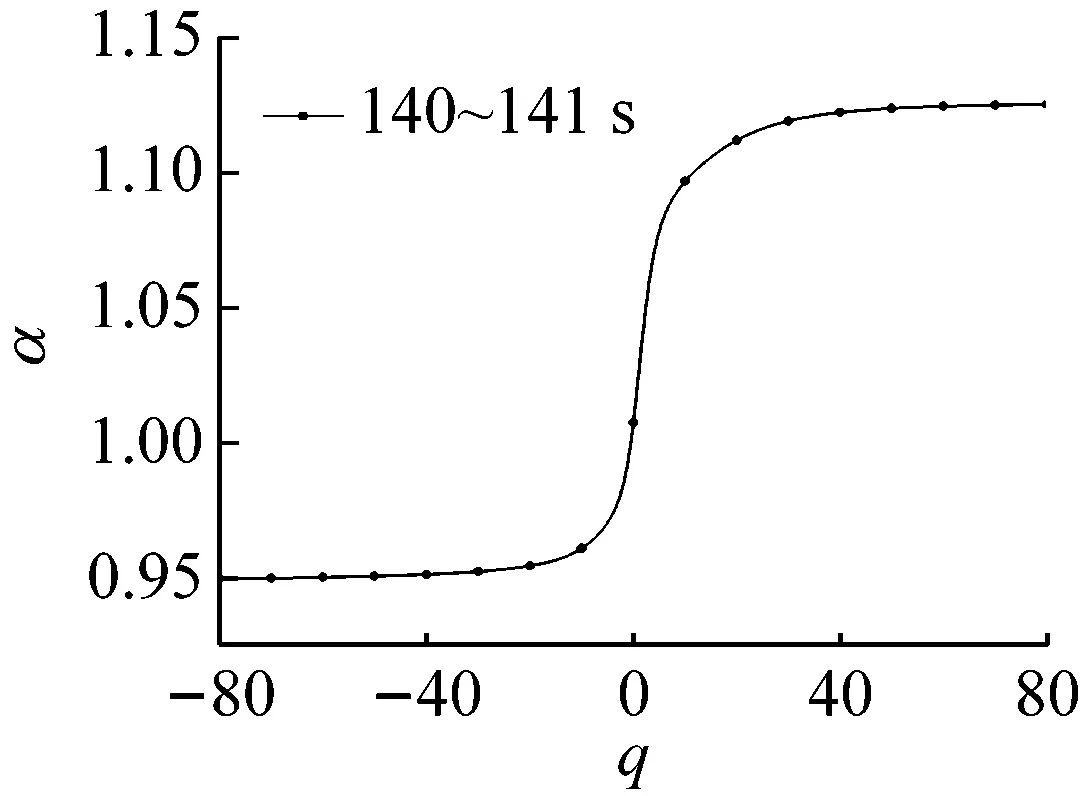
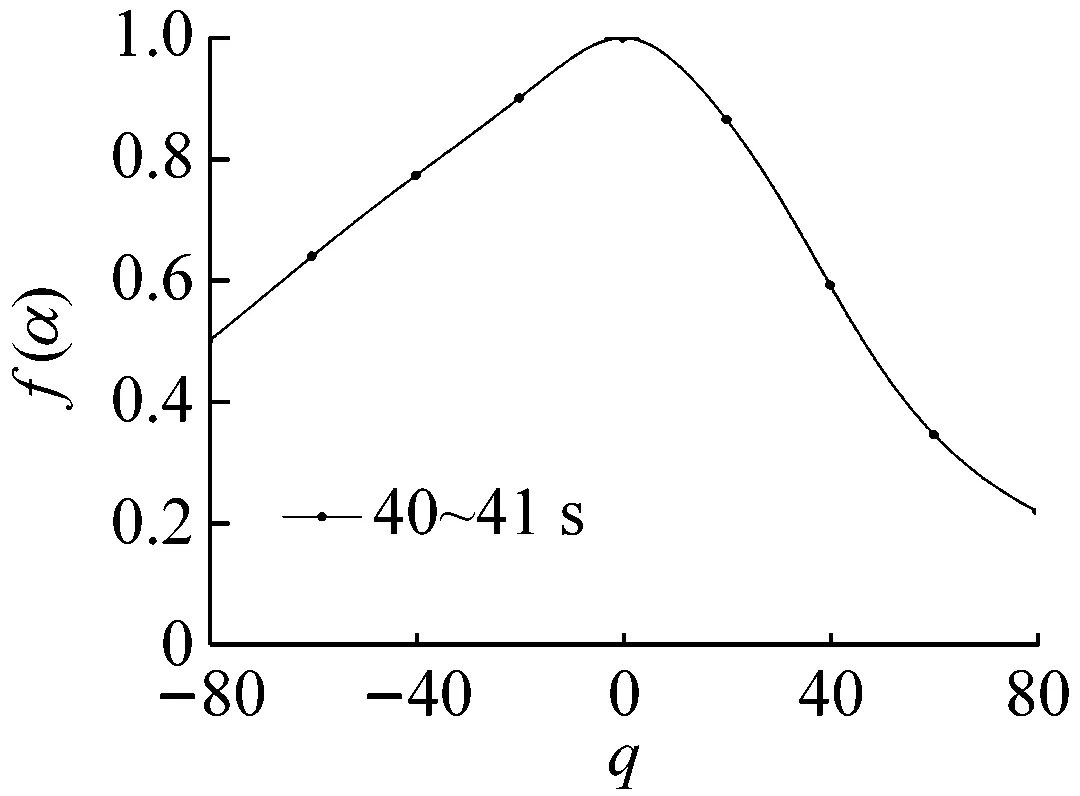
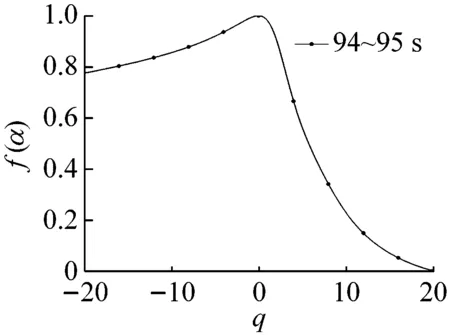
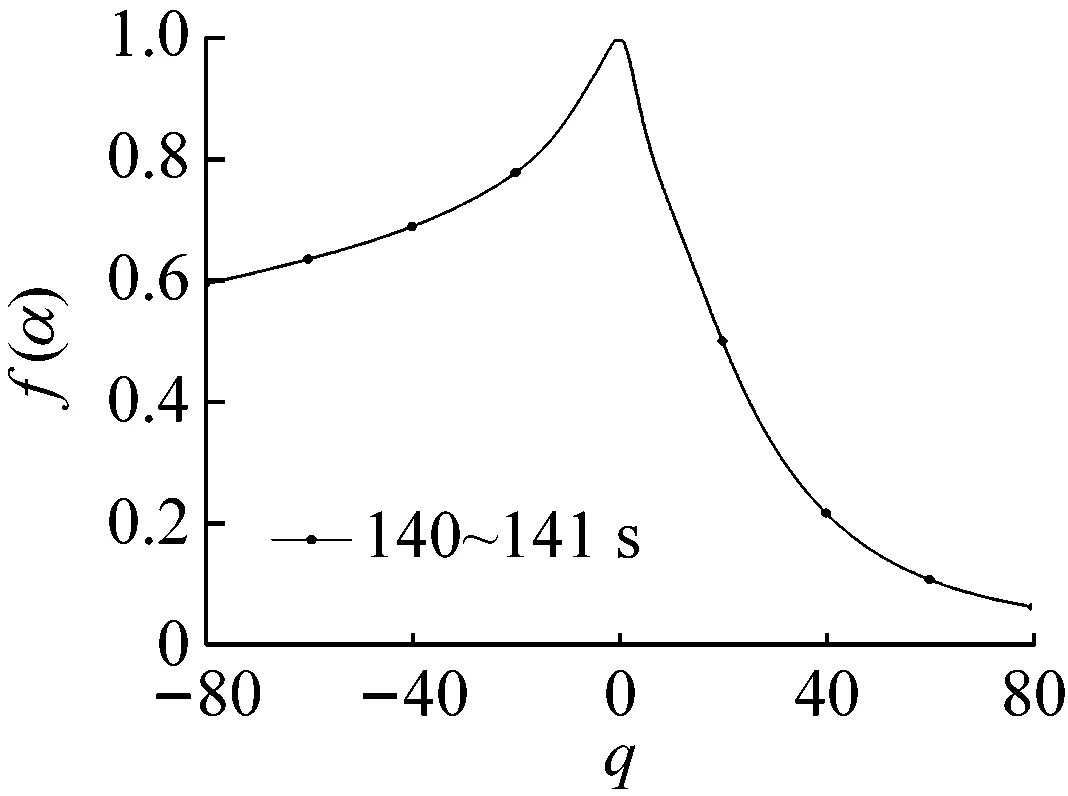
3.4 离心压缩机出口动态压力的多重分形谱参数
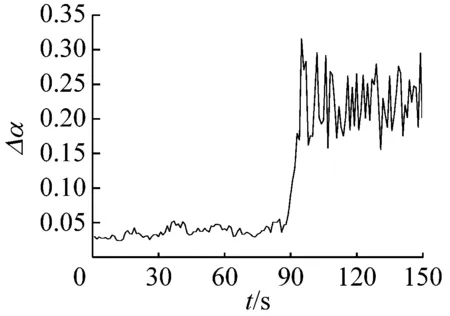
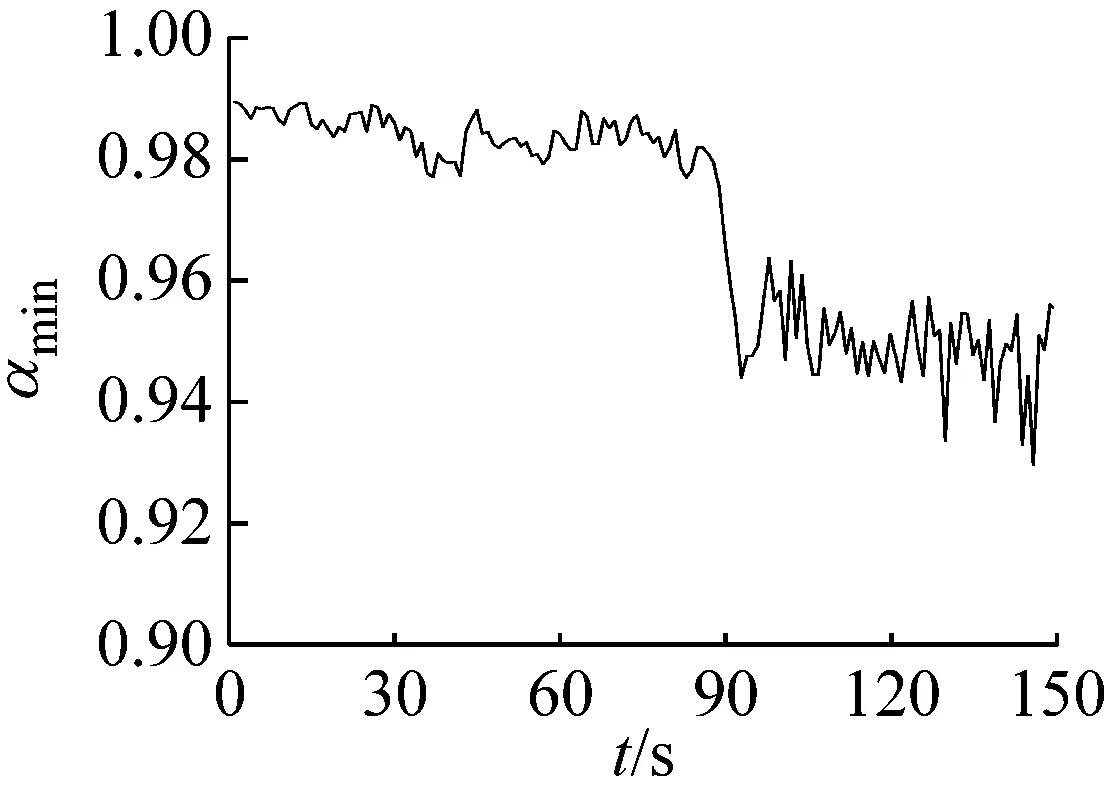
4 结 论
