基于BP神经网络的导线脱冰跳跃高度预测模型
2021-01-16黄桂灶吕中宾
文 楠, 严 波, 林 翔, 黄桂灶, 吕中宾, 张 博
(1. 重庆大学 航空航天学院, 重庆 400044; 2. 河南省电力公司电力科学研究院, 郑州 450052)
冰区导线上的覆冰在气温升高、自然风力作用或振动敲击下产生的同期或不同期脱落,会引起导线的不规则跳跃[1]。导线的脱冰跳跃可能会引起各相导线以及导地线之间的间隙小于电气绝缘间隙要求,从而引起闪络、跳闸等电气事故,严重影响输电线路的安全运行。
自20世纪40年代以来,国内外学者采用实验、理论和数值模拟方法对导线脱冰跳跃问题进行了研究。Morgan等[2]在真型输电线路上进行了模拟实验,通过在档中点释放集中载荷模拟导线脱冰后的最大冰跳高度。Jamaleddlne等[3-4]在人工气候实验室利用两档小模型进行脱冰模拟试验,测量了导线的最大跳跃高度、各个悬挂点张力变化以及悬垂绝缘子串的位移和偏摆角等。Van Dyke等[5]通过实验给出导线“拉链式”脱冰跳跃的冰跳高度估算方法。目前实验方法几乎均采用分布集中质量模拟导线上的覆冰,具有近似性,且由于实验代价大,实验研究结果非常有限。Oertli[6]基于能量原理推导出了覆冰导线脱冰后的冰跳高度公式,Wu等[7]基于能量守恒和应力弧垂变化关系得到了计算连续档导线脱冰跳跃高度的迭代方法。理论算法建立在简化模型上,这些简化与实际相差较大,应用受到限制。Kollar等[8]利用有限元方法模拟了分裂导线子导线脱冰动力响应,讨论了导线脱冰跳跃高度。然而,采用有限元方法得到导线脱冰跳跃高度需要建立导线模型,计算脱冰后的动力响应过程,工程设计中使用非常不便。Yan等[9]利用ABAQUS软件模拟研究了不同参数下输电线路脱冰动力响应过程,基于数值分析结果拟合得到导线脱冰跳跃高度的简化计算公式。我国输电线路设计规程[10]中也给出了导线冰跳高度计算公式,该两公式与覆冰导线脱冰前后的弧垂差Δf有关。最近,Huang等[11]利用比例模型试验研究了导线冰跳高度,并对文献[9]中提出的简化计算公式进行了修正。这些算法都需要通过非线性迭代确定导线脱冰前后的弧垂差Δf。
近年,随着人工智能技术的发展,机器学习方法在各个工程领域的应用研究受到了越来越多的重视。Tang等[12]针对列车碰撞问题,结合有限元仿真模拟和并行随机森林算法,建立了基于机器学习的预测模型,可以快速确定任意速度下机车碰撞的力-位移关系。Xu等[13]提出了一种基于微观模型和BP神经网格预测三维多相和多层编制复合材料弹性模量的方法,利用实验验证了模型和方法的正确性。淡淑恒等[14]建立了盆式绝缘子串的有限元模型,进行了电场计算,并利用神经网络算法优化了结构参数。Wang等[15]利用支持向量机和AdaBoost二级分类器研究了输电线路舞动早期预警方法。廖峥等[16]将输电线路预警问题归结为有监督机器学习方法的分类预测问题,提出了一种基于BP神经网络的舞动预警模型,构建了以风速、风向与线路的夹角、相对湿度以及温度为输入特征量的BP 神经网络学习算法。
本文结合有限元数值模拟和机器学习算法,研究基于BP神经网络预测导线脱冰跳跃高度的模型。该模型可以克服有限元计算效率低的缺点,避免采用工程简化方法时计算导线脱冰前后弧垂差Δf,仅需输入线路结构参数和覆冰脱冰参数即可快速计算出导线的脱冰跳跃高度,为冰区输电线路绝缘设计提供参考,同时,该模型还可以作为冰区运行线路脱冰跳跃引起电气事故的预警模型。
1 导线脱冰动力响应参数分析
1.1 有限元模拟方法
文献[3,9]指出,在冰区连续档线路设计中,一般取奇数档按等档距考虑,验算导线脱冰时的跳跃高度,因此本文采用的连续档模型均为等档距线路。Yan等的研究结果表明,对于奇数档线路,当中间档整档完全脱冰时导线的脱冰跳跃高度最大;且杆塔的变形对导线脱冰跳跃高度的影响很小。因而本文在建立有限元模型时忽略杆塔的影响,仅包含子导线、间隔棒、绝缘子串和线夹等。
导线采用索单元模拟,索单元只能承受拉伸不能承受压缩载荷,在ABAQUS有限元软件中可以通过将空间杆单元的材料设置为不可压缩实现[17]。研究表明单元长度取0.5 m可以满足单元收敛性要求。间隔棒可简化为由直径为0.05 m的圆杆构成的框架,根据模型与实际间隔棒重量相等计算其等效密度。线夹也做近似的简化,计算其等效密度时,还需加上悬垂联板的重量。绝缘子串简化为直径为0.15 m的直杆。间隔棒、线夹和绝缘子串均用梁单元离散。绝缘子串与导线之间约束三个平动自由度,释放转动自由度,间隔棒和线夹与导线之间完全固定。绝缘子串、线夹和间隔棒等金具的弹性模量取2.0×105MPa,泊松比取0.3。
要准确确定导线的阻尼十分困难,阻尼对导线脱冰后振动的衰减过程影响较明显,但是其在一定的取值范围内对导线脱冰后第一个振动峰值影响很小,该峰值决定了导线的最大脱冰跳跃高度。Roshan等[18]在模拟导线脱冰时,提出裸导线的阻尼为临界阻尼的 2%,覆冰导线取临界阻尼的10%,本文模拟中导线的阻尼比采用此取值。
考虑作用于导线上的自重和覆冰载荷,假设覆冰均匀分布在导线表面,脱冰前导线上总荷载可通过修改其等效密度来模拟,等效密度由导线自重和覆冰载荷确定。而脱冰载荷则可通过修改导线的惯性加速度来模拟,惯性加速度与导线脱冰率有关,具体模拟方法详见文献[9]。所有悬垂绝缘子串与杆塔连接的端点线位移固定约束,可以绕悬挂点自由转动,线路两端与耐张塔相连,设置为固定约束,典型五档连续档线路的有限元模型如图1所示。

图1 五档典型线路有限元模型
1.2 参数分析
要得到有效的预测模型,机器学习算法需要足够的样本集。为此,首先采用有限元方法模拟不同参数条件下导线的脱冰动力响应,获得导线的最大脱冰跳跃高度,为机器学习提供数据集,总共设计了841个组合参数。本节给出部分参数组合条件下,数值模拟得到的导线最大脱冰跳跃高度与各种参数之间的关系,这些参数包括档数、导线分裂数、导线型号、档距、高差、导线的初始张力、覆冰厚度和脱冰率等。
首先分析档数对导线脱冰跳跃高度的影响。图2所示为JL/G1A-500/45四分裂导线在覆冰厚度b=20 mm,中间档100%脱冰时,导线脱冰跳跃高度随档数的变化规律。图2(a)所示为无高差、不同档距情况下的结果;图2(b)为档距l=800 m、不同高差h情况下的结果。可以看出,档数对连续档线路导线脱冰跳跃高度的影响很小,5档以上线路几乎没有区别。因此,后面所有参数分析中均以5档连续档等档距线路为对象。

(a)
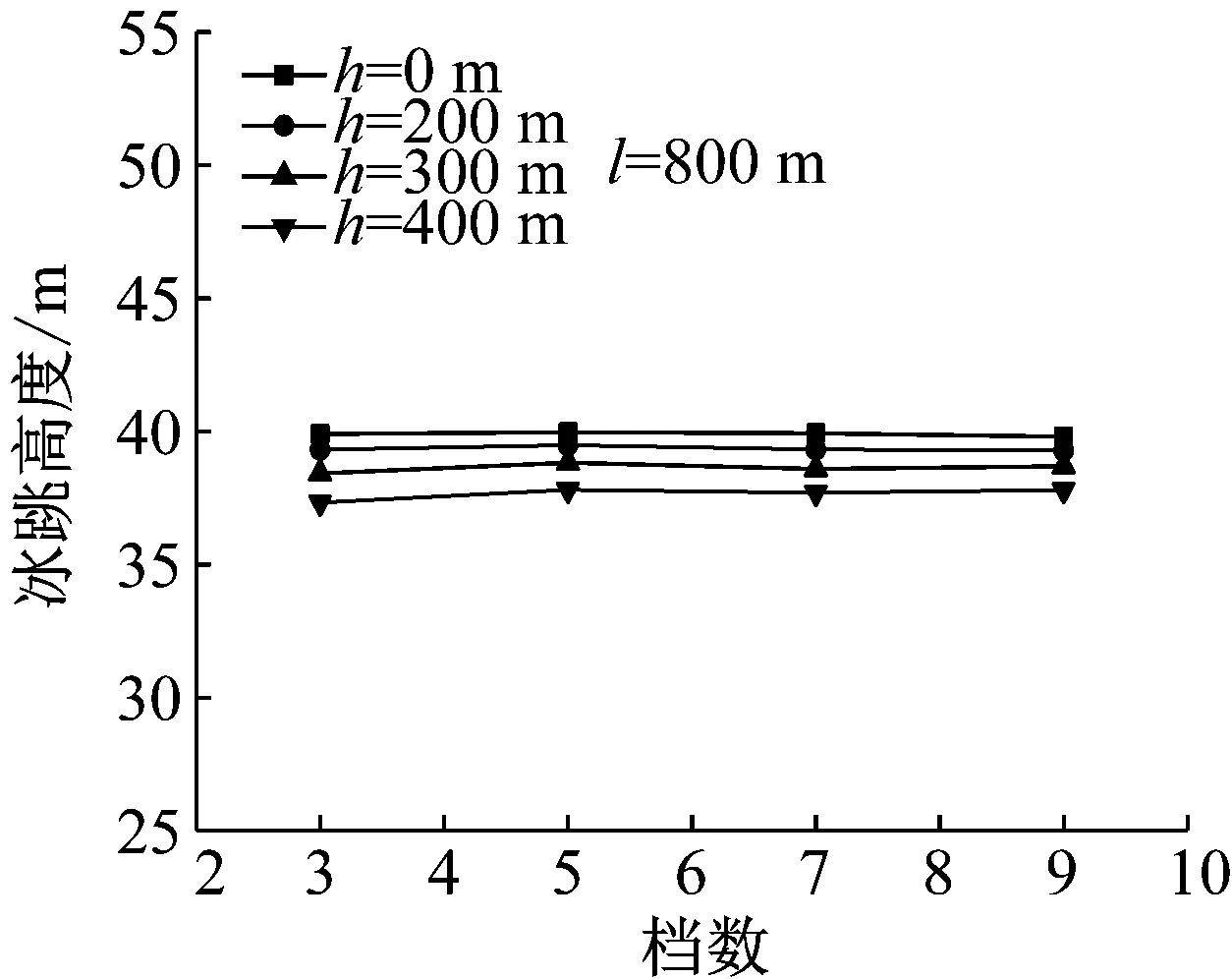
(b)
如图3所示为导线分裂数和型号对脱冰跳跃高度的影响规律。图3(a)为档距500 m,覆冰厚度20 mm,中间档100%脱冰,不同导线分裂数下的脱冰跳跃高度变化规律。可见分裂数越多,冰跳高度越小,这是因为本文所研究的对象中,分裂数越多的导线采用了直径越大的子导线。图3(b)为四分裂导线不同型号导线线路在上述工况下的结果,可见导线型号的不同也会影响导线脱冰跳跃高度。
图4所示为JL/G1A-500/45四分裂线路,不同覆冰厚度,100%脱冰时,档距和高差对导线脱冰跳跃高度的影响规律。图4(a)为无高差时档距对冰跳高度的影响,可见,600 m档距以下线路冰跳高度随档距线性变化,档距大于600 m且覆冰较厚时出现非线性变化规律。图4(b)为500 m档距时高差对冰跳高度的影响规律,可见随着高差的增大冰跳高度有所减小。
图5所示为JL/G1A-500/45四分裂导线,不同高差600 m档距线路,覆冰厚度和脱冰率对导线脱冰跳跃高度的影响。图5(a)为100%脱冰时覆冰厚度对冰跳高度的影响,图5(b)为覆冰20 mm时脱冰率对冰跳高度的影响,显然,冰跳高度随覆冰厚度和脱冰率的增大而增大。

(a)

(b)

(a)

(b)

(a)

(b)
图6所示为JL/G1A-500/45四分裂导线800 m档距下初始应力对冰跳高度的影响。可见,随着初始应力的增加脱冰跳跃高度先增大后减小。
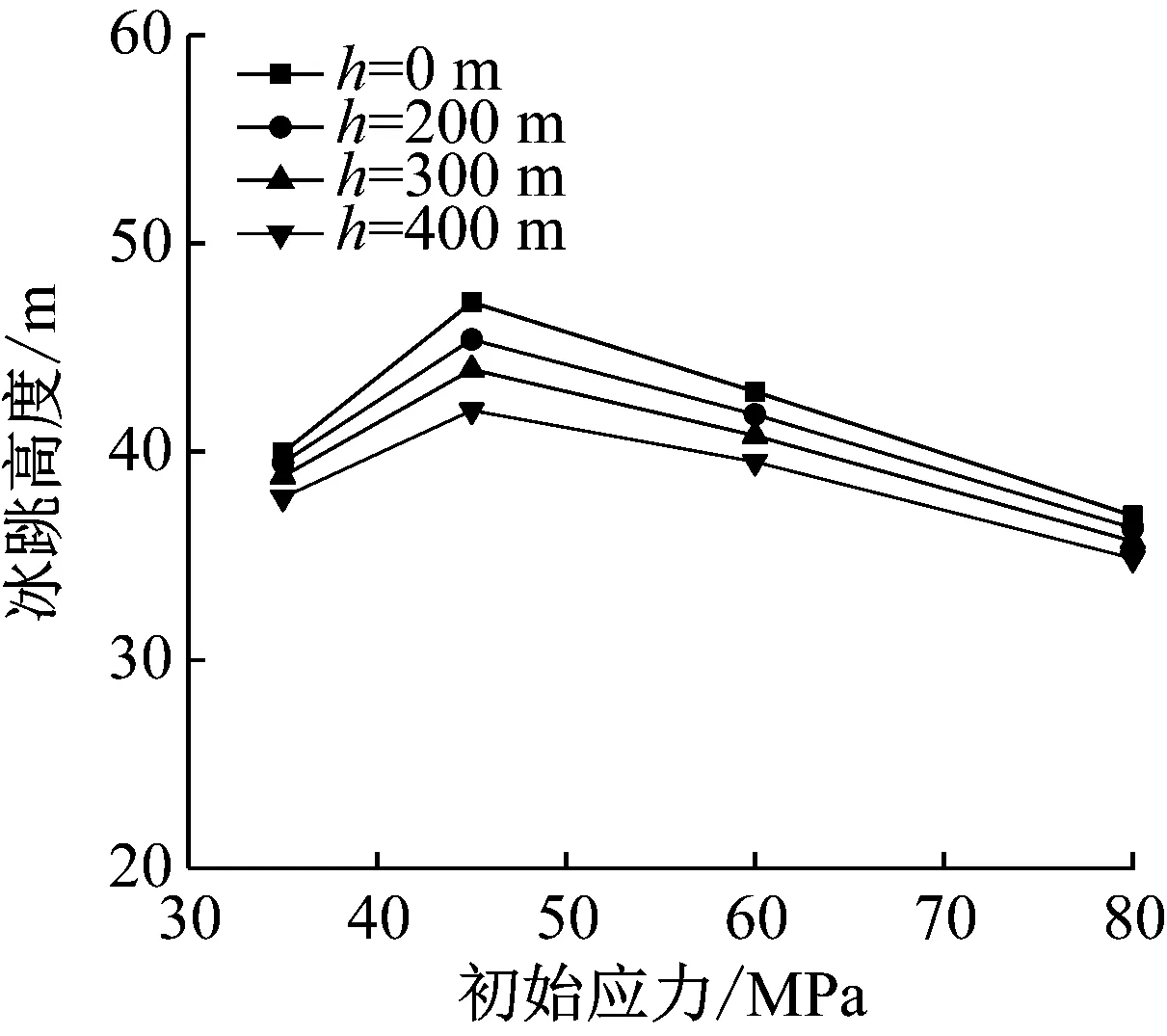
图6 不同档距初始应力对脱冰跳跃高度的影响
限于篇幅,未给出所有参数组合下导线脱冰跳跃高度的变化曲线。从前述结果可见,这些参数对导线脱冰跳跃高度的影响存在复杂的非线性关系。
2 导线脱冰跳跃高度预测模型
2.1 BP神经网络构建
BP神经网络算法具有很强的非线性映射能力以及较强的泛化能力,本文将采用这一算法。BP神经网络包含一个输入层、至少一个隐含层以及一个输出层,如图7所示。其包括数据信号的正向传播以及误差的反向传播两个过程,即计算误差按照从输入到输出的方向进行,而权值和阈值的调整则是从输出到输入。在此条件下,保证隐藏层神经单元足够多就能够模拟一定程度内的任意复杂非线性映射,当映射能力不足时就加入新的隐含层[19]。

图7 三层BP神经网络拓扑结构图
根据第1章的参数分析结果,选择影响冰跳高度的线路结构参数导线分裂数、导线型号、档距、高差,以及载荷参数初始应力、覆冰厚度和脱冰率作为输入变量,与之对应的导线脱冰跳跃高度为输出。激励函数是描述上层节点输出和下层节点输入之间关系的函数,分别采用有sigmoid函数,tanh函数以及Relu函数及其改进型激励函数进行训练,发现使用tanh函数的训练效果最好,这是因为tanh函数在特征相差明显时效果较好。另外,选择均方差作为损失函数,优化算法选择Adam算法,该算法具有收敛速度快,学习效果好,可以纠正学习率消失或高方差参数更新导致损失函数波动较大的问题。建模过程中,初始学习率设置为0.001,既可以保证快速顺利找到损失函数的最小值,又不至于过大反复震荡。
值得一提的是,作为输入变量的7个参数之间数值差异较大,这种差异会影响神经网络对于不同参数的敏感性从而导致训练结果较差;且激励函数使用tanh时一定要对输入层数值进行归一化,否则激活后的值会容易进入平坦区达到饱和,使隐层输出全部趋同。因此首先对输入数据做归一化处理,提高网络的学习效率和泛化能力。最后,BP神经网络需要在不断训练中调整权重和阈值,训练次数太少,会导致精度不够,而训练次数太多又可能出现过拟合。隐藏层层数和隐藏层单元数要随着网络训练结果进行修改,最终调整为隐藏层层数设置为3,前两层有64个单元,最后一层有32个单元。
2.2 模型训练
模型训练时需要训练集和验证集。训练集是用于模型学习的数据样本;验证集是在训练过程中预留出来的样本,可以用于模型的调参和对其能力的初步评估。对训练数据集的划分分别使用了留出法和交叉验证法。经过比较,随机排列的K-Flod交叉验证对数据学习最充分,效率最高。
样本集为第1章中数值模拟得到的841个有效结果,其中训练集包括681个样本,验证集包括76个,另外84个作为测试集。评估指标包括解释方差得分、平均绝对误差、均方差和拟合优度,这些指标用于指导调参过程。经过试验后得到训练次数在6 000次比较合理,图8给出了训练结果,横坐标Epoch为训练次数,Train loss为训练集上的损失函数值,Val loss是验证集上的损失函数值。可以看出训练集和验证集损失函数都趋近于0,说明损失函数已经收敛。

图8 BP神经网络训练结果
2.3 脱冰跳跃高度高度预测
本节针对测试集中的84个样本,将每个样本的7个参数作为输入,由前面得到的BP神经网络模型预测导线脱冰跳跃高度,并与我国输电线路设计规程[10]和文献[9]给出公式的结果进行比较。我国输电线路设计规程使用如下公式计算导线的脱冰跳跃高度
H=m(2-l/1 000)Δf
(1)
式中:l为档距;Δf为覆冰导线脱冰前后的弧垂差;m为考虑导线部分脱冰引入的常数,在整档完全脱冰时取1.0。
文献[9]基于数值模拟结果,通过线性回归的方法总结得到了以下计算脱冰跳跃高度的简化公式
H=1.82Δf
(2)
利用BP神经网络模型以及式(1)和(2)预测的导线脱冰跳跃高度和数值模拟结果进行比较,如图9所示。从图中可以看出,由BP神经网络模型预测得到的脱冰跳跃高度与有限元模拟结果吻合很好,最大相对误差为15.58%,其中仅4个样本的相对误差大于10.0%,1个样本的相对误差在5.0%~10.0%,其它均小于5.0%。利用式(2)得到的结果在脱冰跳跃高度较小的情况下吻合很好,但在脱冰跳跃高度较大时简化公式计算结果偏小,最大相对误差为38.17%,误差大于10.0%的样本多达35个。利用式(1)计算的结果与数值模拟结果偏差非常明显。该三种方法预测得到的导线脱冰跳跃高度的准确度如表1所示,可见与式(1)和(2)相比,BP神经网络模型的计算精度大幅度提高。

(a) BP神经网络模型
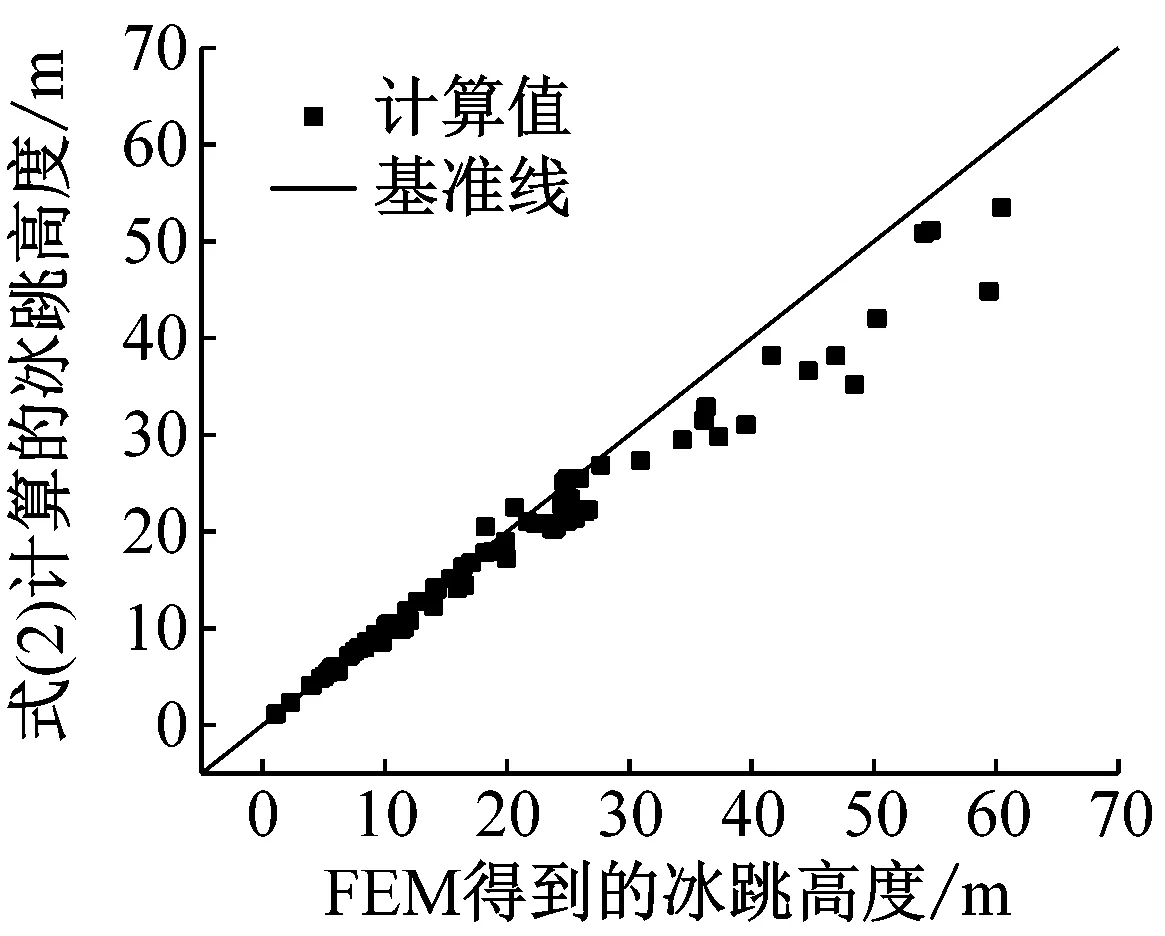
(b) 式(2)

(c)式(1)

表1 不同方法预测导线脱冰跳跃高度的准确度
3 结 论
本文采用有限元方法模拟不同参数下导线脱冰动力响应,得到不同参数组合条件下导线的最大脱冰跳跃高度,基于数值模拟结果得到BP神经网络导线脱冰跳跃高度预测模型,得到如下结论:
(1) 利用ABAQUS有限元软件数值模拟不同参数下的脱冰跳跃高度,得到了841个数据样本。分析表明,结构参数和载荷参数对导线脱冰跳跃高度的影响存在复杂的非线性关系。
(2) 构建了基于BP神经网络的覆冰导线脱冰跳跃高度预测模型,通过网络训练和优化调参,得到了具有较强泛化能力的预测模型。
(3) 利用测试集的样本数据,验证了BP神经网络预测模型的准确度。相对于现有方法,该模型的计算精度和效率得到大幅度提高,为冰区输电线路绝缘设计提供了有效的依据。
