基于RBF积分滑模的无人艇集群协同路径跟踪控制
2021-01-16施文煜曲星儒滕建平
施文煜, 梁 霄, 曲星儒, 滕建平
基于RBF积分滑模的无人艇集群协同路径跟踪控制
施文煜, 梁 霄*, 曲星儒, 滕建平
(大连海事大学 船舶与海洋工程学院, 辽宁 大连, 116026)
为满足船舶护航、目标围捕等任务要求, 文中提出了一种基于路径参数循环的欠驱动无人艇集群协同路径跟踪控制方法。在运动学设计方面, 结合视线制导与一致性算法, 设计无人艇集群协同制导律, 得到闭曲线上对称的编队队形, 实现对目标点进行围捕。在动力学设计方面, 考虑动力学模型不确定性及传统滑模导致的抖振问题, 利用神经网络逼近特性和饱和函数, 设计基于自适应径向基函数神经网络的分布式积分滑模控制器, 保证无人艇能够精确跟踪制导信号, 从而提高系统抗干扰性和路径跟踪精度。Lyapunov稳定性分析证明了闭环系统误差是全局渐近稳定的。仿真结果表明了所提出集群协同控制方法的有效性。
无人艇; 集群; 协同路径跟踪; 视线制导; 积分滑模; 自适应径向基函数
0 引言
水面无人艇(unmanned surface vessel, USV)作为一种无人海洋智能运载平台, 拥有体积小、航速快以及机动性强等特点, 在军事和民用领域都有着极其广泛的应用前景。随着海洋作业任务的日趋多样化, 单USV难以满足其实际应用需求。在此背景下, 构建多USV集群系统, 令多个USV协同完成作业任务成为全球发展趋势。
协同控制问题作为构建USV集群系统的基础, 近年来已成为各国学者研究的热点, 并取得了丰富的研究成果。目前, 常见的协同控制方法主要包括: 领航跟随法[1]、基于行为法[2]、虚拟结构法[3]和人工势场法[4]等。Ghommam等[5]基于虚拟结构法, 利用李雅普诺夫直接法和反步法设计了一种无人艇集群路径跟踪控制器。Hong等[6]研究了领航跟随方法和可变互连拓扑的多智能体系统一致性问题, 在考虑领航者状态不断变化且不可测的情况下, 基于邻居信息设计局部控制器, 使得各智能体都能跟随领航者且保证领航者状态估计误差有界。李芸等[7]将领航跟随法与人工势场法相结合以弥补单一领航跟随控制方法过于集中控制的不足。然而, 上述控制算法在存在局部极小值及目标不可达问题时, 无法保持稳定的编队队形, 而一致性协同控制方法可基于个体信息交互, 使集群系统中各USV信息在控制律作用下趋于一致, 以实现稳定的编队队形。对于多USV系统一致性问题, 通常基于矩阵理论、代数图论、稳定性理论和控制理论等理论知识以及相关的数学建模和USV系统的局部通信关系拓扑来进行研究。Jadbabie等[8]基于Vicsek模型, 引入图论、线性系统理论以及动态系统理论等对算法进行线性化, 使各智能体在有界的区域内网络拓扑结构保持联通的情况下, 各智能体位置和速度的运动方向在控制器的控制下最终实现一致。文献[9]基于路径跟踪控制以及一致性算法来设计编队控制策略, 以实现复杂海况中编队的协同控制, 但并未考虑航行器个体之间通信时延和编队通信拓扑切换等因素对编队协同控制的影响。Wang等[10]设计了一种分布式控制律, 通过路径参数设计一致性算法, 使各航行器在跟踪上几何路径的同时保持期望的编队队形, 但并未考虑海流干扰和参数不确定性的影响。
从上述文献可以看出, 多USV集群协同跟踪控制研究已取得了一些显著的成果。文中研究了一种在外界干扰和模型不确定情况下的无人艇集群协同目标包围控制方法。将视线(line-of-sight, LOS)制导与基于一致性协议的协同方法结合, 以保证无人艇集群能在圆曲线上均匀分布。利用积分滑模面设计动力学控制器对纵向推力以及转艏力矩进行控制, 使各无人艇快速稳定跟踪期望路径。考虑了实际环境中存在的外界干扰以及模型不确定性, 利用径向基函数(radial basis function, RBF)神经网络的逼近特性来逼近未知非线性项, 提高控制精度及系统抗干扰能力。
1 问题陈述
1.1 USV模型
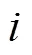
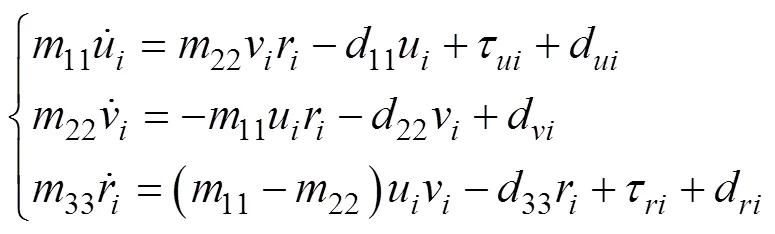
和

考虑USV在运动过程中存在漂角, 运动学模型可表示为
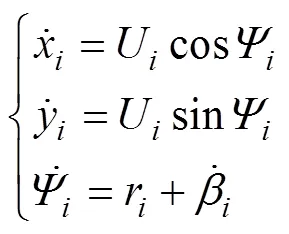
式中: 表示第艘USV的实际航行方向, 且,其中为漂角; 表示其实际运动速度大小。
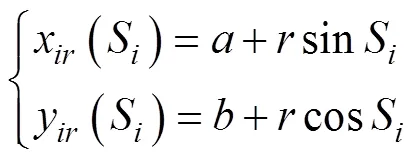
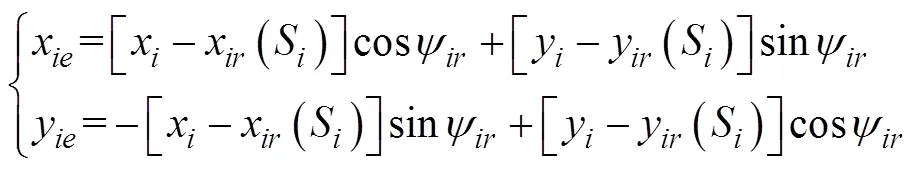
对上式求导并将式(3)代入可得误差动态方程
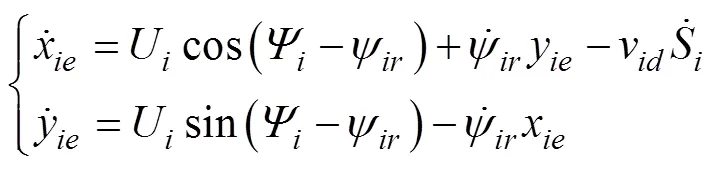
1.2 控制目标
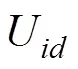
1) 路径跟踪控制目标
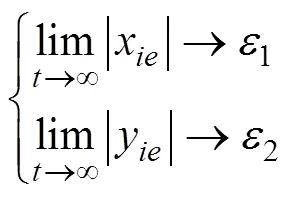
2) 参数协同控制目标
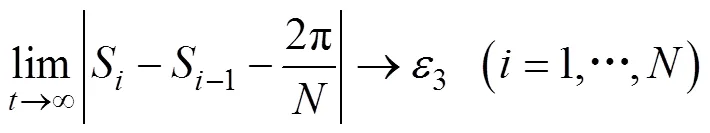
在运动学层次, 基于LOS制导方法设计期望速度和角速度, 并结合一致性协议设计路径参数协同算法; 在动力学层次, 设计分布式速度控制器和角速度控制器, 驱动无人艇跟踪期望路径, 实现编队目标包围。
2 控制器设计及稳定性分析
2.1 制导律设计
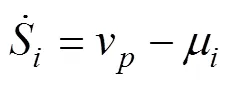
将上式代入式(6), 路径跟踪误差方程可改写为
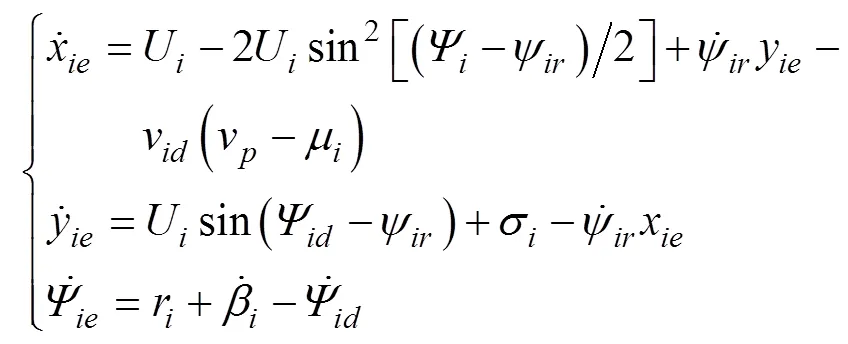
航向制导角

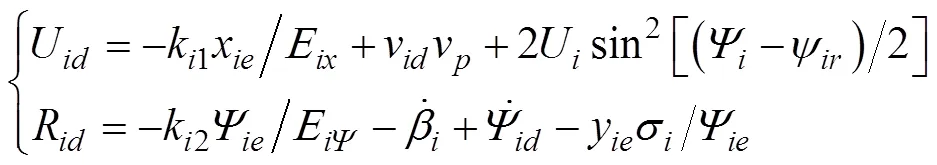
将式(12)代入误差动态方程可得
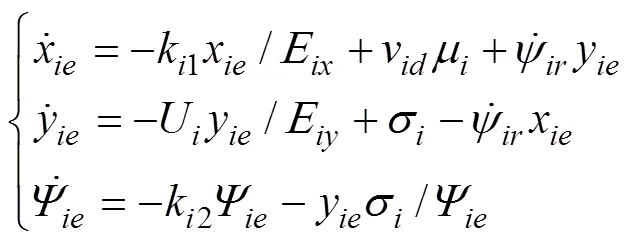
2.2 一致性协议
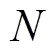
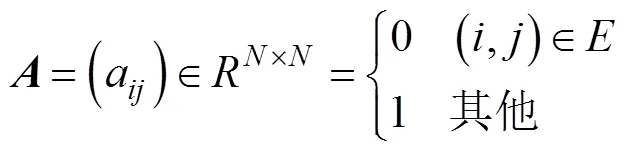
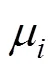
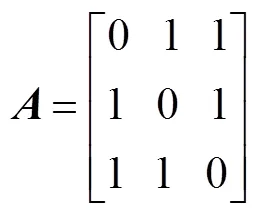
则
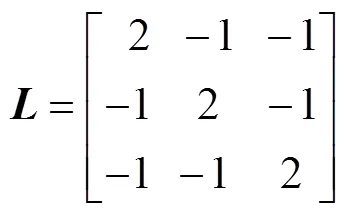
每艘动态的USV都满足动力学特性
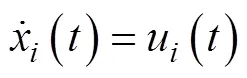
当且仅当每艘USV都满足协议
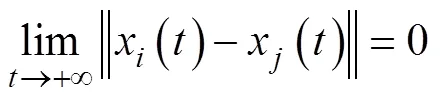
为使路径参数均匀分布, 设计基于相邻USV信息的路径参数更新律[14], 定义参数协同误差为
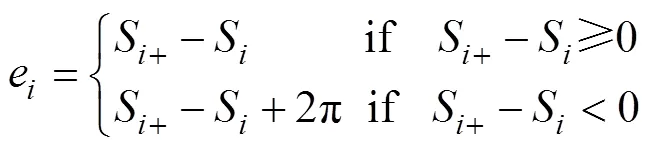
设计更新律为
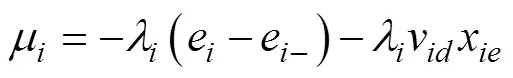
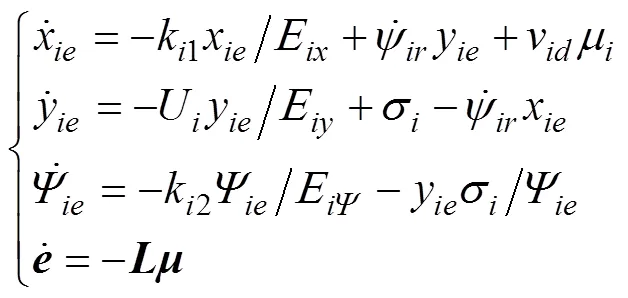
建立如下Lyapunov函数
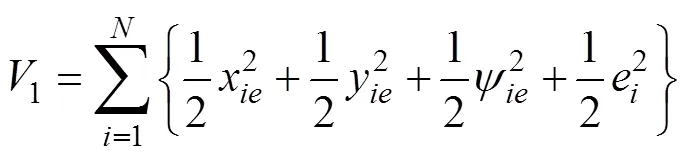
对式(22)求导, 并将式(21)代入可得
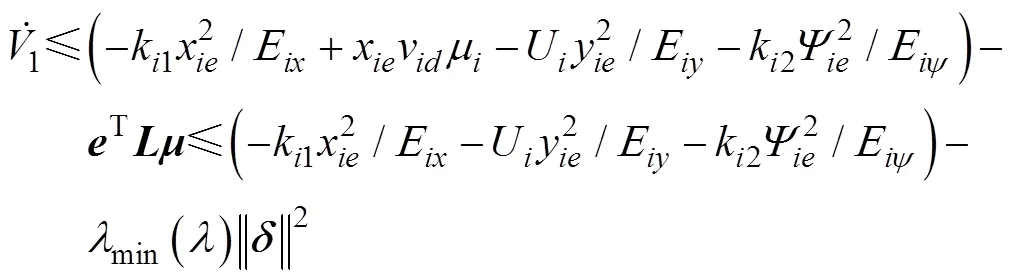
2.3 动力学控制器设计
USV在运动中会受到很多不确定性的影响, 包括自身模型存在较强的非线性和不确定性, 以及外界环境干扰。因此, 利用RBF神经网络快速逼近非线性函数的特性, 设计网络权重和实际控制律, 对模型不确定因素以及外界干扰在线估计。
考虑模型不确定及外界干扰, 动力学模型(1)可改写为
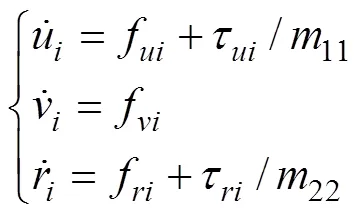
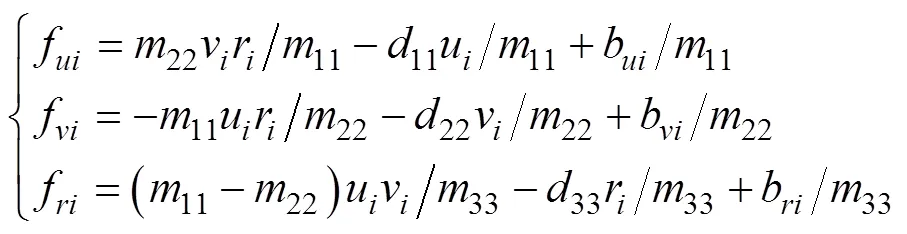
定义纵向速度及艏向角积分滑模面为
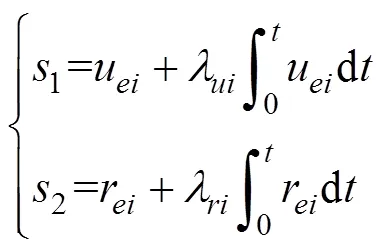
对上式求导得
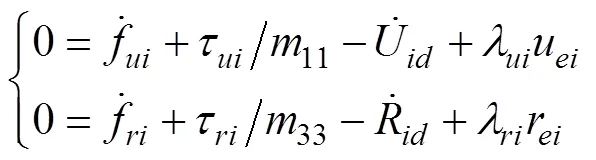
为了消除抖振, 选取指数趋近律为
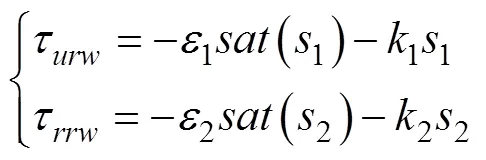
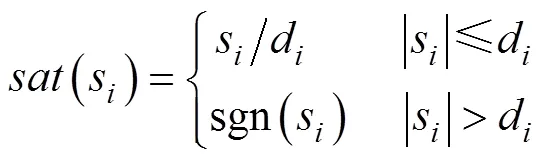
根据式(27)~式(29), 设计纵向速度和艏向角控制律为
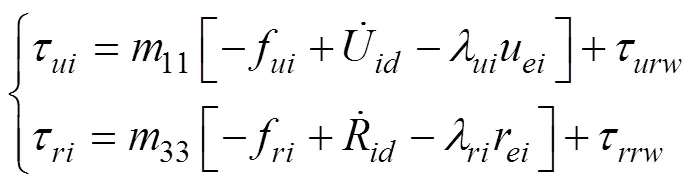
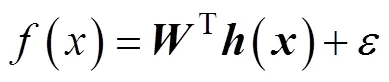

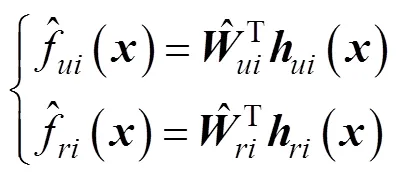
将RBF神经网络逼近算法代入自适应控制器中, 可得控制律为
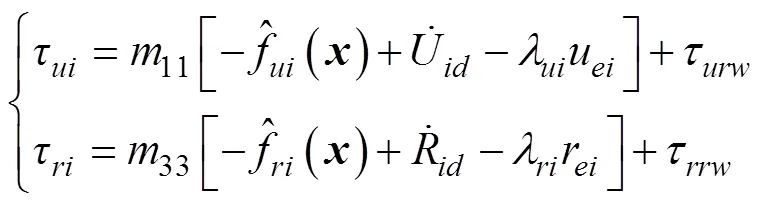
设计自适应律为

纵向速度与艏向角度误差为
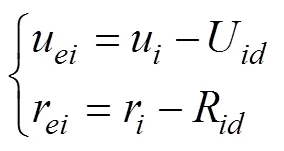
RBF神经网络估计误差为
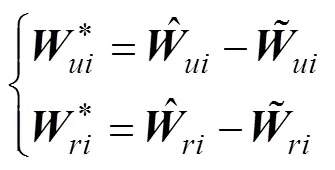
将式(34)代入式(24), 则闭环系统可表示为
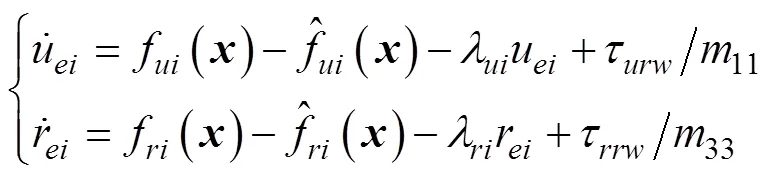
定义神经网络逼近误差
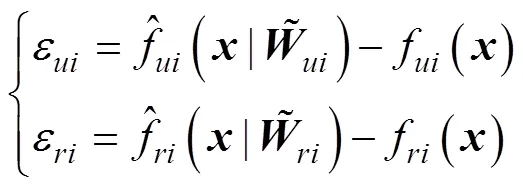
则式(38)可改写为

将式(31)代入式(38)可得
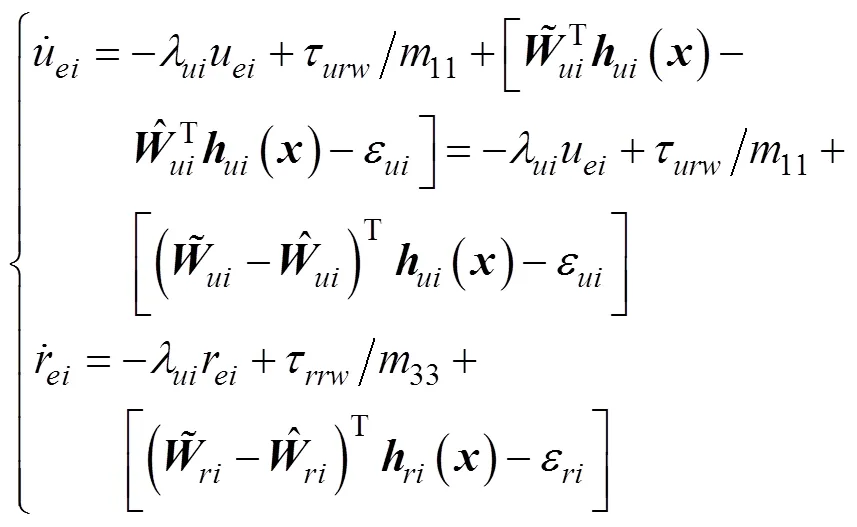
构建如下Lyapunov函数
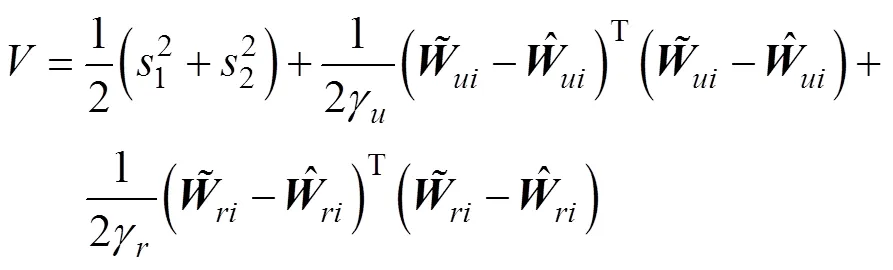
对上式求导并将自适应律代入可得
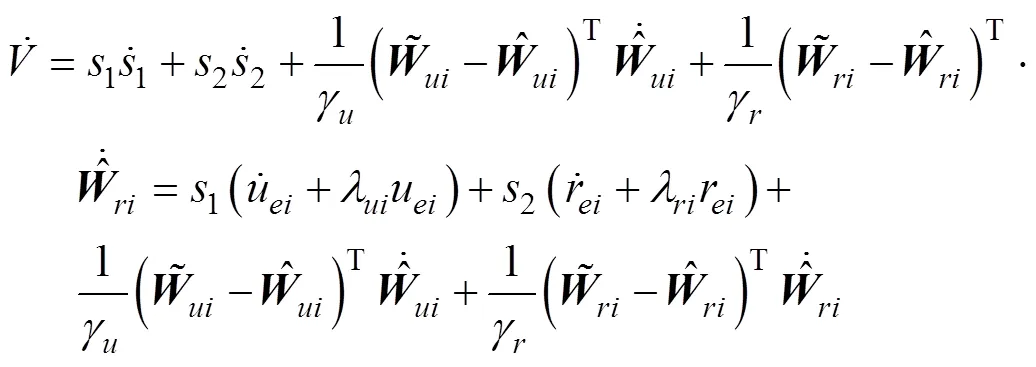
将式(41)代入上式可得
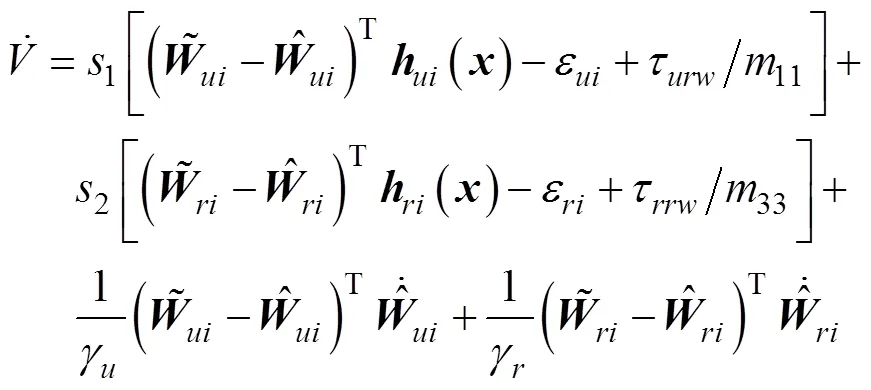
根据式(28)可得
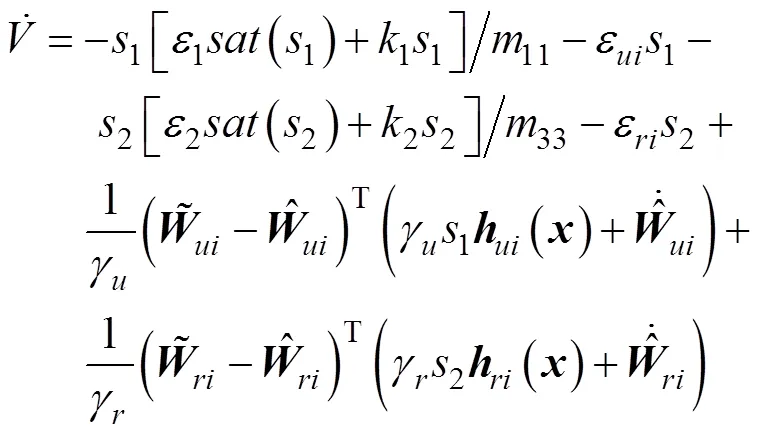
已知自适应律为式(35), 代入上式可得
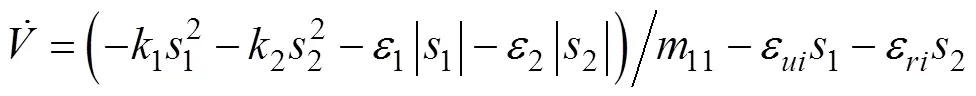
3 仿真试验
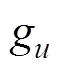
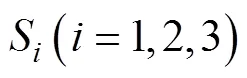
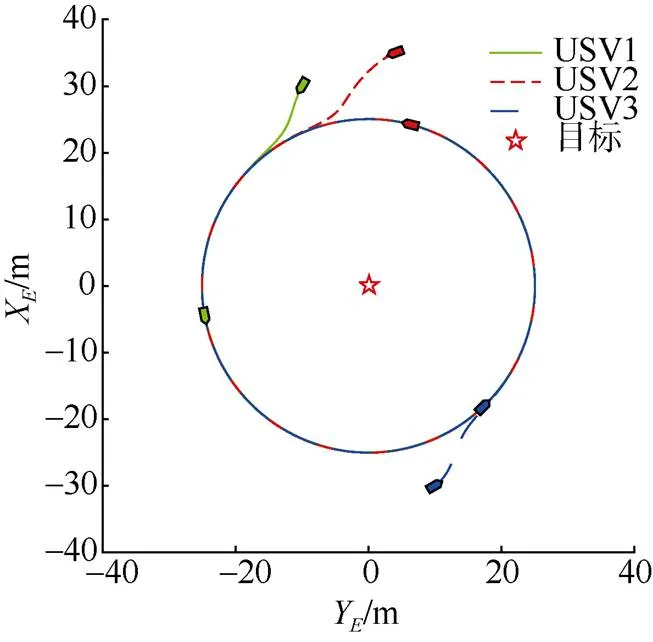
图3 协同目标包围仿真图
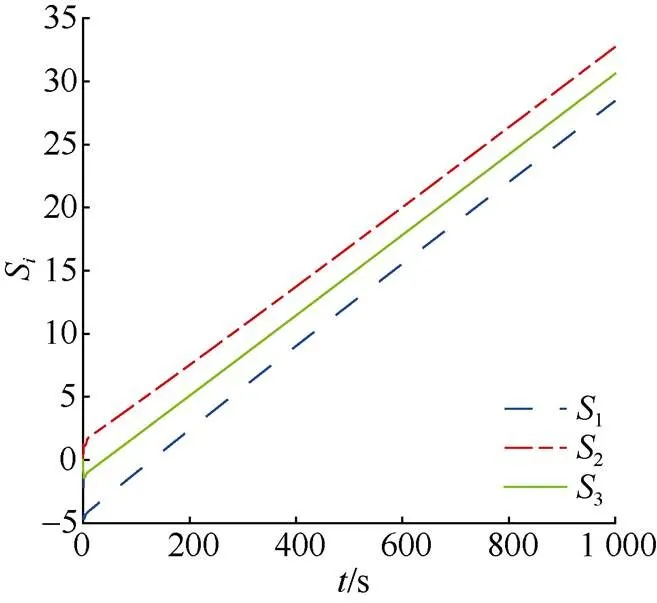
图4 无人艇路径参数曲线
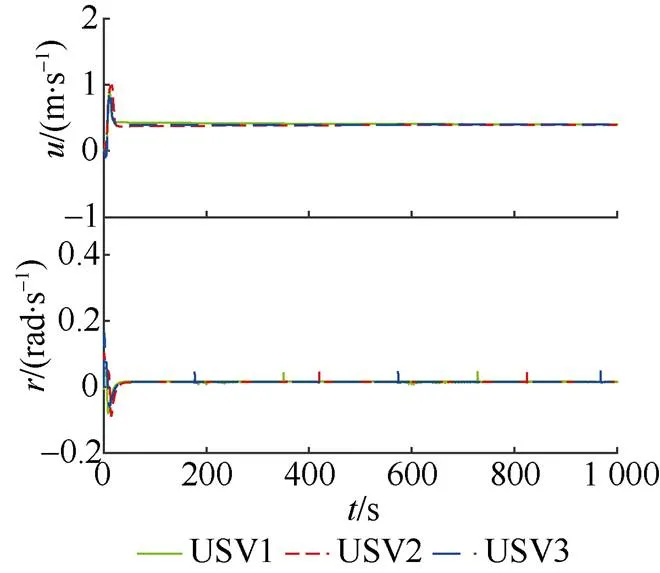
图5 纵向速度与转艏角速度曲线
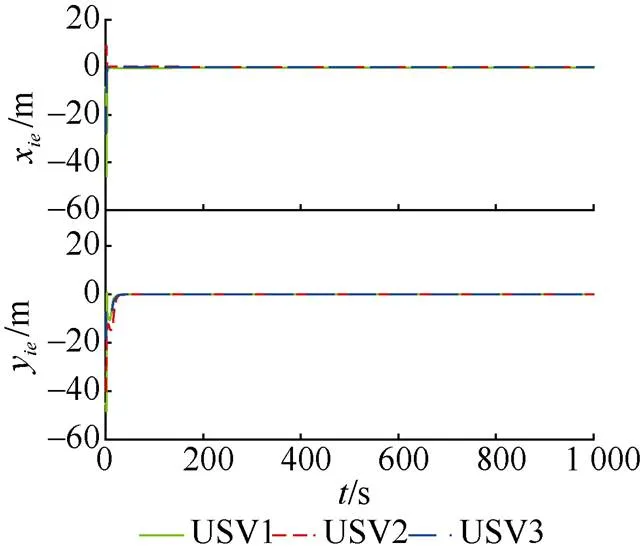
图6 跟踪误差曲线
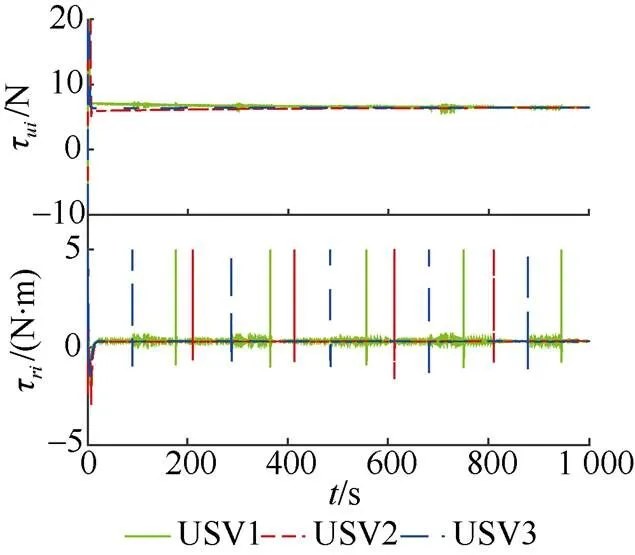
图7 纵向推力与转艏力矩响应曲线
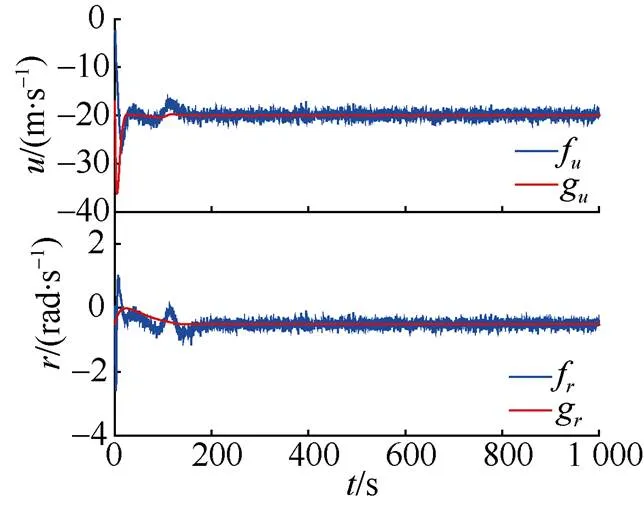
图8 未知非线性项估计
4 结束语
文中研究了一种在外界干扰和模型不确定情况下的无人艇集群协同目标包围控制方法。与现有研究方法相比, 文中方法具有以下优点:
1) 将LOS制导与一致性算法相结合提出了协同LOS制导律, 实现多USV集群协同路径跟踪;
2) 文中针对目标围捕等实际应用采用一种路径参数循环跟踪的方法实现闭曲线上对称的编队队形;
3) 文中设计的分布式积分滑模控制器能有效减弱系统抖振, 提高系统的抗干扰性和路径跟踪精度。
Lyapunov稳定性理论证明了闭环系统的稳定性, 仿真试验验证了协同控制器的有效性。未来将就各无人艇通信中存在的时延和无人艇集群拓扑变换等问题进行研究, 使之具有更广泛的工程应用意义。
[1] Edwards D B, Bean T A, Odell D L, et al. A Leader-Follower Algorithm for Multiple AUV Formations[C]// Gertrude Castellow Ford Center in Oxford USA IEEE/ OES Autonomous Underwater Vehicles. Oxford: IEEE, 2004: 40-46.
[2] Lee G, Chwa D. Decentralized Behavior-based Formation Control of Multiple Robots Considering Obstacle Avoidance[J]. Intelligent Service Robotics, 2018(11): 127-138.
[3] Kwak J H, Kang H D, Kim C H. The Formation-keeping of Multiple Mobile Robots Using Chained-poles[C]//Fukuoka Japan: ICROS-SICE International Joint Conference, 2009: 5695-5698.
[4] Jie J, Khajepour A, Melek W W, et al. Path Planning and Tracking for Robot Collision Avoidance Based on Model Predictive Control With Multiconstraints[J]. IEEE Transactions on Vehicular Technology, 2017(66): 952-964.
[5] Ghommam J, Mnif F. Coordinated Path-Following Control for a Group of Underactuated Surface Vessels[J]. IEEE Transactions on Industrial Electronics, 2009, 56(10): 3951-3963.
[6] Hong Y G, Hu J P, Gao L X. Tracking Control of Multi-agent Consensus with an Active Leader and Variable Topology[J]. Automatica, 2006, 42(7): 1177-1182.
[7] 李芸, 肖英杰. 领航跟随法和势函数组合的船舶编队控制[J]. 控制理论与应用, 2016, 33(9): 1259-1264.
Li Yun, Xiao Ying-jie. Combination of Leader-follower Method and Potential Function about Ship Formation Control[J]. Control Theory & Applications, 2016, 33(9): 1259-1264.
[8] Marasco A J, Givigi S N, Rabbath C A. Model Predictive Control for the Dynamic Encirclement of a Target[C]//American Control Conference. Montreal, Canada: IEEE, 2012: 2004-2009.
[9] 肖瑞武, 孙洪飞. 欠驱动水下航行器编队协同控制[J]. 集美大学学报(自然科学版), 2015, 20(6): 428-434.
Xiao Rui-wu, Sun Hong-fei. Coordinated Control over Formation of Under-actuated Underwater Vehicles[J]. Journal of Jimei University (Natural Science), 2015, 20(6): 428-434.
[10] Wang Y, Yan W, Huang Y, et al. Path Parameters Consensus Based Formation Control of Multiple Autonomous Underwater Vehicles in the Presence of Ocean Currents[C]//17th International Conference on Methods and Models in Automation and Robotics. Miedzyzdroje, Poland: MMAR, 2012: 427-432.
[11] Liang X, Qu X R, Hou Y H, et al. Distributed Coordinated Tracking Control of Multiple Unmanned Surface Vehicles under Complex Marine Environments[J]. Ocean Engineering, 2020(205): 1-9.
[12] 张先迪, 李正良. 图论及应用[M]. 北京: 高等教育出版社, 2008.
[13] 段敏. 多智能体系统分布式包围控制[D]. 重庆: 重庆大学, 2015.
[14] Olfati-Saber R, Murray R M. Consensus Problems in Networks of Agents with Switching Topology and Time-delays[J]. IEEE Transactions on Automatic Control, 2004, 49(9): 1520-1533.
[15] Liang X, Qu X R, Wang N, et al. A Novel Distributed and Self-Organized Swarm Control Framework for Underactuated Unmanned Marine Vehicles[J]. IEEE Access, 2019, 7: 112703-112712.
[16] Liang X, Qu X R, Wang N, et al. Swarm Control with Collision Avoidance for Multiple Underactuated Surface Vehicles[J]. Ocean Engineering, 2019, 191: 1-10.
[17] Liang X, Qu X R, Hou Y H, et al. Finite-time Sideslip Observer-based Synchronized Path-following Control of Multiple Unmanned Underwater Vehicles[J]. Ocean Engineering, 2020, 205: 107941
1. 徐鹏程, 曾庆军, 陈尧伟, 等. 基于导管螺旋桨负载的ROV推进器滑模控制[J]. 水下无人系统学报, 2020, 28(5).
2. 王香, 张永林. 基于RBF神经网络的AUV路径跟踪分数阶滑模控制[J]. 水下无人系统学报, 2020, 28(3).
3. 霍宇彤, 郭晨, 于浩淼. 欠驱动AUV三维路径跟踪RBF神经网络积分滑模控制[J]. 水下无人系统学报, 2020, 28(2).
4. 姜晓奇, 刘维亭, 魏海峰, 等. 基于全阶状态滑模观测器的混合永磁记忆电机磁链观测[J]. 水下无人系统学报, 2020, 28(2).
5. 李鑫, 黄茹楠, 丁宁. 输入受限的自主水下航行器自适应反演控制[J]. 水下无人系统学报, 2019, 27(6).
Collaborative Path Tracking Control Method of USV Cluster Based on RBF Integral Sliding Mode
SHI Wen-yu, LIANG Xiao*, QU Xing-ru, TENG Jian-ping
(School of Naval Architecture and Ocean Engineering, Dalian Maritime University, Dalian 116026, China)
To meet the requirements of ship escorts and target enclosure, a collaborative path tracking control method for underactuated unmanned surface vessel(USV) cluster based on a path parameter cycle is proposed in this study. In a kinematics design that includes line-of-sight guidance and a consistency algorithm, a collaborative guidance law is designed for the USV cluster. This design realizes symmetrical formation on a closed curve and target enclosure. In a dynamics design in which model uncertainties and chattering induced by the traditional sliding mode are considered, a distributed integral sliding mode controller based on an adaptive radial basis function neural network is designed. This distributed integral sliding mode controller uses the approximation characteristics of the neural network and the saturation function to ensure that the USV can track guidance signals accurately, thereby improving the anti-interference of the system and path tracking accuracy. The study also conducts a Lyapunov stability analysis to show that the errors of the closed-loop system are globally asymptotically stable. Simulation results reveal the effectiveness of the proposed collaborative path tracking control method.
unmanned surface vessel(USV); USV cluster; collaborative path tracking; line-of-sight guidance; integral sliding mode; adaptive radial basis function(RBF)
施文煜, 梁霄, 曲星儒, 等. 基于RBF积分滑模的无人艇集群协同路径跟踪控制[J]. 水下无人系统学报, 2020, 28(6): 626-633.
TJ630; U675.7; TP273.2
A
2096-3920(2020)06-0626-08
10.11993/j.issn.2096-3920.2020.06.006
2020-09-27;
2020-11-03.
国家自然科学基金资助项目(51879023); 辽宁省兴辽英才计划资助项目(XLYC1907180); 辽宁省自然科学基金资助项目(2019-KF-01-16).
梁 霄(1980-), 男, 教授, 博导, 主要研究方向为无人海洋航行器决策与控制技术.
(责任编辑: 许 妍)
