非均匀介质驻波声场纹影法成像及其声速测量的改善

陈水桥， 程诗卓， 郭 鹍， 陆子毅， 许熠辉

（浙江大学a.物理学系；b.竺可桢学院，杭州310027）

0 引 言

声场作为一种常见的物理场，由于其不便观测、稳定性差而在生活中的应用相对较少，且应用点往往集中于驻波声场。为了更加方便地研究驻波声场的特性，将其可视化无疑是一种直观且高效的方法［1-2］。纹影法基于声波与光波的一般作用规律：声场介质密度随声场的发生而改变，继而引起折射率的变化。当一束光穿过声场介质时，能够形成稳定的相位光栅，出现相应的纹影图像［3］。与其他方式相比，纹影法具有直接、快速、不破坏声场的优势，不仅为驻波声场静态特征的研究提供了一个更为直观可感的途径，其非侵入性更是适用于声场的动态与连续性研究。可视化作为一大优势，将难于测量的压力数据转化为易于测量的光强数据，为实验精度提供了保障，运用后期处理技术，还可使所得结果更为明显、美观，便于进一步分析。本实验利用超声波驻波声场的声辐射压力在空间中呈周期分布的性质，再结合纹影法，对非均匀空气介质中的超声波形成的驻波声场进行成像，并进行相关处理，使得能够直观反映出超声波驻波声场的某些特性，进而更加精准测量其波长以及其他关联数据。为使图像更加形象可视，在MATLAB中对图片做灰度直方图均衡化之后［4］，使得图像中原来灰度值分布集中的区域分布到其他区域，从而使得图像灰度值整体范围变大，某些局部灰度细节变化可见，从而达到增强图像对比度和清晰度的效果。并在此后进一步用图像处理工具进行了加工，再进行灰度-颜色映射处理，得到较好伪彩色纹影图。最后测量了声波速度，验证了实验效果。最后，还用数理方法分析了仪器系统的灵敏度。

1 基本原理

1.1 驻波声场形成原理

气体介质中驻波声场的形成综合利用了超声波的波动特性与能量特性［5］。如图1 所示，在声源对面设有反射度良好的反射装置，设声波波长为λ，L 为生源与反射端距离。由声源发出的超声波经反射端反射，反射波与原波频率相同、传播方向相反，当声源处与反射端相距L 为λ／2 的整数倍时，两者相干形成稳定驻波。

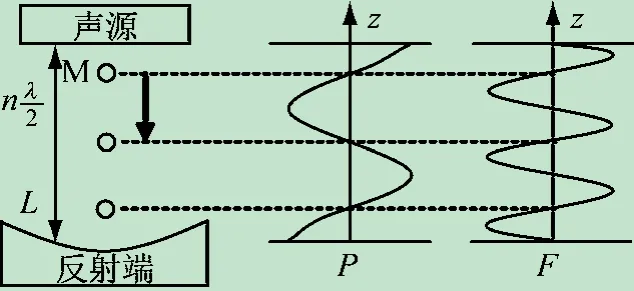
图1 驻波声场形成原理图

另外，由于超声波的能量特性，超声波声场改变了声源与反射端间的气体介质的密度分布，进而形成声场作用下的辐射压力。图1 中辐射压力为F，M 为一质量较小物体，P 是波源发出的声波的沿z 轴方向的振幅。

设两列相干波的波函数表达式为

将两类波合成为

可见，声辐射压力F沿波动方向为周期分布［6］。由于声辐射压力具有回复力的特性，此时如果将物体M置于波节处，当样品偏离平衡位置，就有被拉回原位置的趋势，当其位置相对于平衡位置有微小偏移时，会在附近做小振幅振动，最终在波节附近实现物体的悬浮。

1.2 纹影法成像原理

纹影法是一种将光通过相物体引起的相位分布转换为光强分布的方法［7］。如图2 所示，对于Z 型透镜光路，设通过相物体的入射光为

图2 纹影法成像原理示意图

通过相物体引起相位滞后（通常相位滞后很小），可表示为

式中：第1 项代表直射光；后1 项含有φ，它包含了相物体分布的信息，这两项的相干叠加构成了屏幕上相物体的像。由于相物体与周围介质在边缘具有折射率梯度，如果相物体折射率大，会使光线向相物体方向偏折，使得其区域与背景产生照度差异，从而使得相物体像的相位差异转化为照度差异，相物体可见（为方便起见，之后的讨论将主要简化为几何光学）。

1.3 非均匀介质中光的传播原理和偏折角推导

在均匀介质中光沿直线传播，而当介质中出现湍流、热对流等干扰因素时，会导致同一透明介质的局部折射率n发生变化，使得光线传播发生扰动。扰动区域的图像会与周围的图像形成差异，即可见阴影。

透明介质的折射率为

在标准大气中，对于可见光，格拉斯通-戴尔常数k≈0.23 cm3／g［8］。式中：空气密度ρ 的两个量级变化能引起n的值变化30%，因此若想通过光学手段观察密度变化小的气体，需要非常灵敏的光学设备。

忽略光的相干性，简化为几何光学。取右手直角坐标系x，y，z，令z 轴为未受扰动时的光线传播方向，x、y轴构成的平面垂直于z轴，如图3 所示。接下来证明，光的不均匀性所导致光的折射和弯曲程度与x、y平面内各自折射率梯度成正比［9］。

图3 非均匀介质中光传播的几何光学分析图

假设纹影光路为在x、y方向上各向同性的二维光路，即沿z 轴对称。图3 中，假设垂直折射率梯度dn／dy ＜0，且忽略在x、z轴上的折射率梯度变化，认为初始时刻通过z1的是平面波，波阵面垂直于水平光轴z轴。当波前通过被测对象，即从z1到z2时，设不同的微分时间Δt 对应微分距离Δz，折射的偏折角度为Δε。由于光线始终垂直于波前阵面，通过z1的水平光线同样有Δε的偏折角。

定义n ＝c0／c，其中本地光速为c，真空光速为c0。由图3 可知，

不同时刻Δt有Δt ＝Δz（n／c0），合并得：

当Δy→0 时，方程中n／（n1n2）可以简化为1／n。令所有微元趋近于0，可得：

由于ε是非常小的角度，因此可近似为dy／dz，即图中的斜率。将其代入导数后，可以得到：

该式揭示了折射梯度大小与折射光线曲率的关系。由此，在x、y轴方向上，光线的偏折角经积分可得

式中：n0为周围介质的折射率。

可以看到，光线的折射取决于折射率梯度，光线总是朝着n值较高的方向弯曲。而对于气体而言，光线总是朝着密度ρ较高的地方弯曲。这些非均匀透明介质所产生的梯度扰动即为纹影。所以，纹影图像也揭示了偏转角度的存在。

2 仪器系统

本文采用离轴单反射镜系统，主要包括声场系统和光学系统两大部分。其系统原理示意图如图4所示。

图4 仪器系统示意图

图中，声场系统需要让两个超声波换能器之间产生驻波声场［10］。根据当时的实验条件（温度、湿度等），计算出在该条件下超声波的理论波长λ，并预先将两个超声波换能器的间距调整为3λ。打开电源后稍微调整换能器间距使泡沫塑料小球能够在该声场中悬浮，由此来检验驻波声场的形成。本文应用的超声波发生器选用科美达可调频率功率超声波发生器，能够产生20 ～40 kHz的高频信号，最大功率300 W。超声波换能器采用28 kHz，60 W的压电陶瓷。

光学系统主要由球面反射镜、狭缝器、刀片和照相机组成。点光源用LED光源，可连续调节光强。球面反射镜的镜面直径203 mm，焦距800 mm。成像设备采用佳能EOS 80D 单反相机。在确认驻波声场的形成后，就对光路进行细致的调整以在相机中观察到驻波声场的纹影图像。方法如下：将点光源与一个光屏靠在一起，在之前确定的水平面上同时前后移动，找到一个图像最清晰、像点最小的位置，即球面镜的焦点。将点光源固定在焦点附近，用刀片挡掉一定量的光。调整刀片挡光量（约80% ～90%）、相机的位置、快门时间以及ISO以得到尽量大且清晰的纹影图像。其中球面反射镜放置在光源的曲率半径轴上（R ＝2f）。发散的光束将充满反射镜并且以相同的路径返回，在光源处形成光源的像。通过在光源和图像光束之间设置较小的离轴分离，并加入刀口即可构建与前一个纹影系统有相似效果的纹影系统。在焦距很大时，两个纹影系统的测试区域可以近似。测试区位于接受光源发散光的反射镜前，理想情况下，同一光束会两次横穿测试平面上的点，每次横穿时都会产生一个偏转角ε。

3 实验与分析

3.1 图像的获取与处理

调节相机参数，快门时间1／200 ～1／800，ISO80-160，帧率50，拍摄视频，截取其中效果较明显的帧如图5 所示。然后，在MATLAB中对图5 进行全局灰度增强和直方图均衡处理，使得纹影细节放大，调节效果如图6 所示。

图5 相机拍摄纹影图

图6 直方图均衡处理纹影图

在Lightroom中调节曲线，对图6 进行对比度、锐化、亮度调整，得到图7 效果图。再在MATLAB 中对图8 作灰度-颜色映射，得到伪彩色图。

图7 图像工具处理纹影图

图8 伪彩色纹影图

3.2 声速测量

游标卡尺测量超声波振子直径数据如表1 所示。

表1 超声波振子直径测量数据

所以u（D）＝0.04 mm，得到振子直径为D ＝（5.820 ±0.004）cm。

设超声波振子直径对应像素值为Δm，纹影波相邻两条彩色条纹间距对应像素值为Δn，其比值为

对图10 中多个条纹坐标进行测量，所得数据如表2 所示。为配合测量比值δ 需要，其中Δn 未连续测量，而是任意选择最清楚的条纹测量。

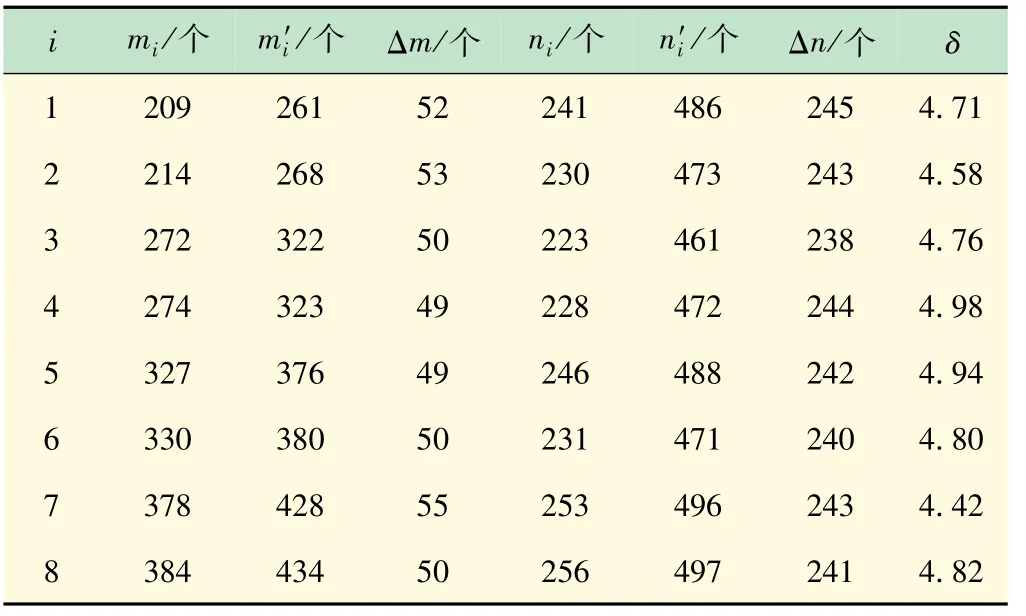
表2 条纹坐标测量值

又因为v ＝λ／T，λ ＝D／δ，T ＝1／f［11-12］，所以推导得声速测量公式为

已知超声波发生器所用频率f ＝28.013 kHz，Δ仪＝1 Hz。所以将上述测量值代入式（9），得到实验声速值：

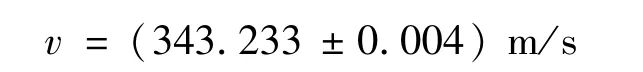
实验时室温为18.4 ℃，根据文献计算得该温度下声速理论值为342.431 7 m／s，所以本方法测量的声速误差较小。

3.3 仪器系统灵敏度分析

纹影光学系统最大的优势就是其灵敏度。它的输出图像为x、y轴的二维图像，图像特征由成像的缩放以及灰度对比决定，灵敏度仅需考虑这两点［15］。为了更方便讨论灵敏度，依然对Z 型反射镜系统进行分析［13，14］。设光源照度为B（cd／m2），假定采用的是一个水平光源狭缝和水平刀口，那么在没有刀口的情况下，纹影图像照度

式中：b为光源狭缝的宽度；h为光源狭缝的高度；f1为第1 反射镜的焦距；放大因子k 为纹影图像相当于测试区域的大小比例。［16］

让刀口阻挡除聚焦的光源像以外的所有光束（刀口成圆孔形），该部分具有高度a。用a 和f1／f2替换光源像的无遮挡实际高度h，f2为第2 反射镜的焦距，则式（10）可改写成

设ΔE 为照明变化值，是纹影图像照度E 与其背景照度E0的增益。假定纹影对象在实验区域有ε 的偏折角，y 轴分量εy将有部分光源图像在垂直刀口平面产生向上偏移距离Δa ＝εyf2，代替式（11）中的a，

则有

得到了测试区εy偏折形成的对应图像点的照度增益。

设对比度为C，指图像点对于一般纹影照度增益ΔE与纹影照度E的比值，即

设纹影灵敏度为s，也称对比灵敏度，定义为图像对比度比折射角度的变化率，即

对于单反射镜纹影光路，旁轴近似下，该结论也类似，第2 反射镜的焦距等于第1 反射镜的焦距，即单镜的焦距。

由此说明，在观察范围一定时，反射镜的焦距影响成像的灵敏度，因此需要一个大焦距的凹面镜。同时，刀口截止的程度也影响着纹影的对比度，因此也可以通过提高刀口截止来提高灵敏度。但刀口截止提高时，测试区域边缘会产生衍射光线，在刀口平面产生二次衍射，产生模糊效应，影响图像分辨，因此刀口截止不能无限提高。

4 结 语

通过自组纹影法测量装置能够直观便捷得到超声波驻波声场的一些性质，并且通过图像处理技术方便了对数据的准确获取。本文用光线折射几何理论证明了光的不均匀性所导致的光的折射和弯曲程度与x、y平面内各自折射率梯度成正比。得到的有关声场的数据和图形比较清晰，并准确测量了声速值，且与理论值误差较小。最后分析了影响成像的灵敏度以及对实验的各种影响因素。