固体表面能测定方法研究进展

王书敏，张丽华,代淑兰

(1.中北大学 化学工程与技术学院，山西 太原 030051；2.中北大学 环境与安全工程学院，山西 太原 030051)

在生产和生活中，界面现象无处不在，几乎每一个物理、化学过程都涵盖了界面体系。因此，通过实验测得物质各种界面能对工业发展和生活便利具有重大意义。在各种界面能中，固体表面能的测定对于高分子材料、多孔材料、涂料、分子筛等多种材料的理论研究和实践应用都有重要指导意义。

表面能概念自提出以来，如何较准确地测得其数值便成为一个需要解决的问题，因为液体表面能可以直接测得，但固体表面能只能通过其它测定方法间接获得。因此，许多研究人员对固体表面能的测定从温度外推、溶解热、价键理论、表面应力、接触角力学平衡等不同方面进行了探究。提出了多种固体表面能的测定方法。

1 温度外推法(熔融外推法)

1.1 测定原理

温度外推法是一种经验的通用方法，通过液体表面能的测定方法测得固体在高于其熔点时不同温度下的表面能，然后将温度外推至低温固态下，此时由表面能与温度的关系作回归曲线，得出低温下的表面能即为该固体的表面能[1]。

关于固体熔体表面能测定，可借鉴尹东霞等[2]介绍的液体表面能的测定方法，可利用差分最大压力气泡法、差分毛细管上升法[3]、悬滴法、静滴法等[4]方法测定物质液体或熔体的表面能。

温度外推法测定的过程也可以利用Etovos提出经由Ramsay和Skield[5]修正的关系式来确定固体表面能γ，关系式如下。

rV2/3=K(TC-T-d)

(1)

式中，V为摩尔体积；TC为临界温度；K为常数项；d为常数项。

对于大多数液体d=6.0时，K=2.1×10-7J/K。根据此式，经过计算也能估算出室温下的固体表面能。但此关系式仅适用于有临界温度的固体，对于大部分聚合物或者混合物固体并不适用。

1.2 存在的问题

温度外推法是假设固体物质在固态和液态时表面张力温度系数相同的情况下推出来的经验法[6]，对于不符合假定的固体并不适用，此方法用于可加热至熔点温度以上的无定型固体、碱性卤化物、有机聚合物等物质，但其精度较差，而且必须有一定经验，准确性受到操作人员的经验熟练影响，对于一些熔点很高或者高温下有危险的物质不适用该方法。

温度外推法测定的关键在于液体或熔体的表面能测定的精确，选取适合固体熔点和熔融环境的测定方法，可以提高温度外推法的测定可信度。

2 溶解热法

2.1 测定原理

Lipsett等[7]提出，固体溶解后界面被破坏，固体释放表面能，溶解热增加，使用精密的量热计测量不同粒径物质的溶解热，之后，通过计算物质不同粒径溶解热之间的差值得出总表面能，测定固体的总表面积，便可计算出单位面积固体的表面能。

Lipsett等测定了氯化钠晶体的溶解热，测得的实验结果表明，粒径大的NaCl溶解热为 3 882.75 J/mol，粒径小的溶解热比粒径大的溶解热大66.94 J/mol，当1 kg的氯化钠粗颗粒变为微颗粒时，总比表面积为2.8 m2/g，因此，氯化钠晶体的表面能为0.4 J/m2。

Benson等[8]用吸附法测定氯化钠比表面积，进而测得其比表面能为0.276 J/m，之后，Brunaues等[9]用溶解热法测定了氧化钙、氢氧化钙、水化硅钙在23 ℃时的比表面能分别为1.31，1.18 J/m2和0.386 J/m2，Balk等[10]测定了25 ℃时氯化钾的比表面能为0.252 J/m2。

2.2 存在的问题

Lipsett等提出的溶解热法要求有高灵敏度量热技术且固体是极细的粉体，可溶解于水中，例如卤化碱等可溶性盐固体，对于难溶的高聚物、金属、合金和一些非金属溶解热法不适用。

溶解热法的关键是量热技术和比表面积的测定，要想提高测量的精确度，可以从量热技术和比表面积测定方法进行改进。

3 晶体劈裂法

3.1 测定原理

研究者发现云母晶体具有明晰的解离面，容易分成毫米级的大薄片，采用劈裂功法测定其表面能十分有效，单位面积的劈裂功是固体表面能的2倍，Orowan[5]在研究了云母的性质以后提出了下述的关系式：

(2)

式中，T为薄片厚度为x时的张力；E为弹性模量；γ为所测定的固体表面能。

依据此方法的原理，Lazerew等[11]采用摆及其他不同的力，实验中控制摆所损失的能量等于新产生表面的自由能，测得云母表面自由能数据：干云母2.40 J/m2、湿云母1.77 J/m2，真空测得云母的表面能为4.5×10-4J/cm2，在空气中降为3.75×10-5J/cm2，这些数据表明，解离技术以及环境都会对该测定方法有很大影响。纪国法等[12]借助晶体劈裂功法计算页岩表面能，采用密度、声波时差2种参数获取计算结果，对比分析新的分形方法计算数据、传统方法预测数据与实验测试数据，新的分形方法计算平均误差为3.63%。

3.2 存在的问题

劈裂功法可用于盐、金属、半导体材料等表面能的测定，Orowan测定云母片时其难度大，精度差，测定环境使得形成新表面会有不同的膜吸附，所得结果相差很大，没有可靠的准确性。

对于劈裂过程的深一步探究以及控制测定环境可以使劈裂功法进一步发展，提高该方法的测定可信度。

4 应力拉伸法

4.1 测定原理

固体温度在接近熔点时，原子或分子都会发生一定程度的流动和滑移，当施加拉力时，其应变速度与应力成正比，测定薄片或者丝状固体应变速度与应力之间的关系，向熔点附近的细丝或薄片固体施加载荷，求出应力，测定其单位时间内的延伸长度，即可求得其应变速度。

Alexander等[13]给一根温度在1 273 K细金丝加上载荷，作应力与应变速率关系图，他们发现在载荷小的情况下应变速率与应力几乎呈直线，因此应变速度为零时的应力，恰好等于沿金丝线的表面张力。

该方法求得的表面应力是金熔点附近的近似表面张力(表面能)。Alexander等在1 273 K测定金丝的表面能为1.30～1.70 J/m2，此后，Udine等以此方法测得铜在接近熔点时的表面能约为1.37 J/m2。

4.2 存在的问题

应力拉伸法是测定薄片或者丝状固体的近似表面能，准确性没有得到其它理论和实验数据的验证和支撑，且该方法对固体材料的可延展性有较高的要求。

5 理论估算法

5.1 测定原理

固体的原子或分子相对被固定在晶体的晶格内，因此，知道晶格之间的力学关系，就可以从理论上计算表面能。固体晶体大致可分成离子晶体、分子晶体和金属晶体几种。Harkins等[14-15]用这几种理想晶体作为模型进行了固体的表面能计算。

以金属晶体[15]为例，可以通过蒸发能来计算晶体的表面能，一个原子的键合被破坏可通过升华热的形式表征，新的单位表面形成时，上层与下层的原子键合必然会被破坏。因此，表面能和升华热之间存在关系，例如铜晶体在体相中有12个原子，但是在表面区域周围只有9个原子，所以表面原子升华热能相当于与其他原子间的金属键断裂释放的能量，铜的升华能可测，为3.172×105J/cm，铜原子从体相内部移到表面，要断3根金属键，每个铜原子转移到表面所需的能量为8.78×10-20J。铜每平方米的原子为1.78×1019个，由于铜的临界温度很高，若假定熵的影响可以忽略，铜单位面积的表面能为 1.56 J/m2。

用此方法测得表面自由能与实验测定的相符，对于部分临界温度高的晶体来说是一个很好的计算方法。

Galanakis等[16]提出基于断裂晶体第一邻键数的简单规则，确定铜、银和金3种贵金属的表面能，当一个化学键被破坏时，这些金属的电子电荷的重排实际上不会导致剩余化学键的改变。因此，断裂键所需的能量与表面取向无关，表面能与断裂的最近邻键的数目成很好的近似比例。李晓燕等[17]使用最近邻断裂键(NNBB)模型来拟合Pt、Pd和Au表面的表面能。结果表明，该模型能够较准确地描述上述贵金属的表面能，提出所有元素的表面能和与断裂邻近键数之间都存在线性关系。

5.2 存在的问题

理论估算法要求固体必须是高度规整的晶体，Harkins等以几类理想晶体为模型计算了固体的表面能，Galanakis化学键断裂模型也只是提供理论计算，只适用于晶体的模型，对于非晶体和一些包含晶区与非晶区的高聚物来说，该方法并不适用。

6 表面链接法与电测法

6.1 表面链接法

Kendall[18]提出由表面力链接在一起的两个固体平面，单位面积的两个平面表面之间的界面能定义为Г，即从无穷远处到两个平面表面接触时释放的能量，对于相同的固体，Г是表面能的2倍，即Г=2γ。

Kendall通过实验证明，用球面比用平面更好，更容易达到平衡，两球接触模型见图1。

图1 两个直径为D的光滑球体在零载荷下接触直径为dFig.1 Two smooth spheres with diameter D andcontact diameter d under zero load

Hertz[19]提出可以用以下方程计算出界面能进而求出表面能γ：

d3=3(1-v2)

(3)

式中，d为接触点直径，W为球面上的外部载荷，D为球面直径，E为杨氏模量，v为泊松比。

Kendall提出，式(3)也适用于<1 μm的陶瓷颗粒，但是这种粒子测定表面能的难点是接触点的直径d只有十几纳米，Kendall通过电子显微镜测定了金属和聚乙二醇的接触直径。接触尺寸由粉末的弹性模量决定，得出在零外部载荷情况下，接触点直径与粉体表面能的公式：

d=[9πγD2(1-v2)/E]1/3

(4)

已知固体的直径D、泊松比v以及弹性模量E时，根据测定球体的接触直径便可求出固体的表面能。

6.2 电测法

1990年，Kendall[20-21]提出利用电测法测定粉体的表面能，以式(7)为基础，Maxwell[20]给出的电收缩电导(electrical constriction conductance)用c表示：

c=dC

(5)

式中，d为接触直径，C为球体的体电导率。

接触点粒子的表观电导率用C*表示，则：

C*=C[9πγ(1-v2)/DE]1/3

(6)

一个等球体立方填充的表面能可以通过测量致密电导率C*得到，知道粒子的真实电导率C、直径D和弹性模量E，即可求出固体表面能。

6.3 存在的问题

Kendall提出的表面链接法，是在两球接触模型的基础上测定表面能，Hertz提出的一种计算方程，准确性有待验证，之后Kendall提出利用电测法测定粉体的表面能，是在表面链接法的基础上发展而来，实验要求高，步骤复杂。自从提出该方法后，后来的研究者并没有对之进行实验和理论验证，其可靠性无从考证。

7 接触角法

7.1 接触角测定方法

液体接触固体表面时，平衡后会呈现一定的液滴形状，这是三相界面受力平衡的作用，关系式为：

γgs=γglcosθ+γls

(7)

式(7)就是Yong方程，见图2，θ被称为接触角。

图2 液体在固体表面的张力平衡和接触角Fig.2 Tension balance and contact angle ofliquid on solid surface

接触角测量可以分为角度测量法、长度测量法、力测量法和透过测量法等[22]几类，杜文琴等[23]比较了角度测量和长度测量的适用条件，丁晓峰等[24]介绍了接触角测量的技术。目前，测量接触角的方法有光反射法、竖版毛细升高法、小液滴法(量高法)[25]、躺滴法[26]、斜板法、吊环法、液饼法、表面张力法、曲线拟合法[27]、毛细法[28]、液桥法等[29]。可以根据固体粒径的不同选取适合的接触角测量方法。

7.2 基于接触角计算固体表面能方法

基于接触角计算固体表面能方法是在Yong方程的基础上推导而来的。式(7)中可测量的只有γgl和θ，γgs和γsl目前仍然难以通过实验直接测量，要计算Yong方程中的γgs和γsl，还需建立其他相关的方程来求解，因此，研究者们探索了很多计算表面能的方法，刘永明等[30]介绍了基于Yong方程建立的计算方法。

(1)Fowkes法

Fowkes等[31]认为固体表面能由许多能量分量组成，每种分量是不同的分子之间作用力的表现，各种分量关系为：

γ=γd+γn

(8)

式中，γ是总的表面能，γd和γn分别是由London力引起的表面色散分量和表面非色散分量，得到的计算公式是：

(9)

Kwok D Y等[32]使用1-戊醇和萘烷两种极性不同的液体测定了FC-722的固体表面能，测得1-戊醇表面能与色散表面能相等，得出1-戊醇是非极性分子的矛盾结果。从Kwok D Y的实验结论得出表面能分量途径的Fowkes法不能够反映物理事实。

(2)Owen-Wendt-Kaelble法

Owen与Wendt[33]在Fowkes的方法上进一步改进，认为表面能是另外两种表面分量组成：

γ=γd+γh

(10)

式中，γd是偶极-偶极分量，γh是氢键分量。

Owen与Wendt得到的计算公式为：

(11)

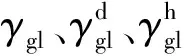
Kwok D Y等[32]用不同的液体测得相同固体的表面能，与Fowkes途径相似，选取不同的液体测量固体表面能，计算得到相同固体的表面能分量都各不相等，因此，采用该方法会预测出极性的固体是非极性的相反结论。选择不同的液体组合得到了相似的结果。

张子阳[35]在Owen-Wendt-Kaelble法的基础上，采用了水-二甲基亚砜(DMSO)、水-甲酰胺、水-乙二醇和水-甘油的二元混合物来测定接触角，建立了混合方程。通过制备平板聚二甲基硅氧烷(PDMS)和硅烷衍生玻璃两种疏水表面，得到了混合液的接触角，利用3种二元混合物测定的PDMS表面能与纯溶剂一致，但不确定度降低到13%以下，当将水-二甲基硅氧烷、水-甲酰胺和水-乙二醇的接触角组合在一起时，不确定度下降到5%左右。

(3)LW-AB法

Van Oss等[36]对表面能分量极性另作解释，认为极性部分是Lewis酸碱作用，即质子的供给电子体系。表面能γ由Lfshitz-van der Waal分量γLW和Lewis酸-碱分量γAB组成，γAB分为Lewis酸分量γ+和Lewis碱分量γ-。因此，对于固体表面能可以表示成以下形式：

(12)

对于固液界面，Van Oss等[36]认为其界面能与各极性分量也符合几何平均关系，得到的计算公式为：

(13)

该方法提出后，Kwok[37]采用LW-AB法计算FC721、Teflon、PET的固体表面能，结果发现，不同液体测定同一种固体的表面能相差很大，而且有出现负值的情况，因此Kwok认为用LW-AB法计算固体表面能并不能反映物质的实际情况。Hollander等[38]则有不同的观点，他认为Kwok选取液体的宽泛性也会导致LW-AB法计算固体表面能数据的不稳定，随后，他们提出了标准检测液体的选取组合：一种非极性液体与两种单极性液体的组合，采用该方法计算的表面能参数具有良好的一致性。Van Oss[39]经过对不同的液体组合的探究，最终发现丙三醇、二碘甲烷、水3种液体重复性最好。Sagit等[40]发现，在液体组合中，如果另外两种液体是不同极性的单极，则误差最小。其液体的性质越相似，相对误差则越大。

Bingjun Han等[41]在LW-AB法的基础上提出了表面粗糙度的概念，对不同粗糙度的接触角进行修正。

cosθw=rcosθ

(14)

式中，θw是测定接触角，θ是真实接触角，r是平滑面积与实际几何面积之比。

结合式(14)得：

(15)

Bingjun Han考虑固体表面的粗糙程度，采用四液法，计算固体表面能。

此外，用接触角计算固体表面能的方法还有很多，如Zisman法、Good-Girifalco[42]法、ZDA[43]法、Wu[44]调和平均法等。

7.3 存在的问题

接触角法是目前测定固体表面能应用最广泛的方法，该方法虽然操作简单，但是用接触角计算固体表面能仍然存在一些问题。罗晓斌等[45]比较了接触角计算表面能的方法，气体吸附[46]的影响、接触角的迟滞现象[47]、线性张力的影响、接触角<35°存在误差等都会影响接触角计算表面能的结果。

接触角法测定固体表面能虽然应用广泛，但目前对它存在较多争议，理论上和计算上有一定的缺陷，所推导的公式均带有假设条件，其测定结果仍只是假定条件的理论解，接触角测量的精确性和各种计算方法假定的分量的可行性仍然需要研究者进一步探究。

8 总结

实验测定固体表面能的方法有限，现有报道的测定方法得到的实验数据，不同测定方法的实验数据之间存在较大的差异，目前没有统一比较公认的测定方法。

针对不同的固体可以选用与其性能相适应的固体表面能测定方法。从溶解度的角度考虑，对于可溶性的固体物质，可以考虑采用溶解热的方法来测定固体表面能；从物质延展性来看，延展性好的固体物质可以用应力拉伸法来测定固体表面能；有明晰片层、易于劈裂的固体物质，可采用劈裂功法测定表面能；从晶体的方面考虑，规整度高的晶体固体，可以从理论估算其表面能，理论估算法也可以为其它实验测定方法提供参考；从固体的粒径尺寸出发，对于一些粉体可以采用表面链接法、电测法以及接触角法测定表面能；聚合物的固体表面能，根据聚合物的可熔性和延展性可以考虑使用温度外推法、应力拉伸法以及接触角法进行测量。

对于固体物质的表面能测量，不同的方法也可以相互提供验证依据，利用适用多种测定方法的固体，通过不同的固体表面能测定方法得到的实验数据可为改进方法提供参考。