基于自适应滑模观测器无位置传感器PMSM控制方法研究

姚艳艳，张会娟，刘建娟，吴才章，陈红梅

(河南工业大学 电气工程学院，郑州 450000)

0 引 言

id=0的矢量控制策略自问世以来便受到大量研究学者的青睐。为了实现永磁同步电机(Permanent Magnet Synchronous Motor，PMSM)的矢量控制需要获取电机转子位置和转速等信息进行实时反馈。采用位置、速度传感器直接测取转子位置和转速信息是较快捷有效的方法[1]。但是该方法仍存在体积大、成本高、引线多以及对环境要求高等问题[2]。为了解决这一问题，多种无位置传感器PMSM控制方法[3-6]相继问世。其中滑模观测器由于具有受电机参数变化影响小、对外界干扰鲁棒性强、响应时间小等优点脱颖而出[7]。

滑模观测器自身的工作机制会给闭环控制系统带来抖振问题。因此，怎么消除和削弱系统抖振成为一个研究难题[8-9]。文献[10]针对滑模观测器存在的系统抖振问题，提出了一种自抗扰控制器为核心的控制方法。该方法可以实现电机转子位置的估计，且具有良好的稳态性能。但是该算法相对复杂，实际应用难度较大。文献[11]提出了一种用滤波后的反电动势信号替代滤波前含有抖振的反电动势信号作为反馈信号的滑模观测器改进方案，削弱了系统抖振，但是该方法采用滤波后的反电动势信号，将产生一定的幅值、相位变化。

本文针对无位置传感器PMSM控制存在的转子位置与转速估计精度不高的问题，提出一种新型的自适应滑模观测器。首先，根据id=0矢量控制原理，建立PMSM数学模型。其次，结合自适应算法和锁相环技术，对传统滑模观测器进行改进。主要改进点是提出一个反电动势自适应估计环节代替传统的低通滤波器，从而提高电机转子位置与转速估计精度。最后，选用200 W的PMSM为被控对象，对该算法进行仿真与实验验证。

1 PMSM数学模型

在α-β坐标系下，电机定子电压状态方程为：

(1)

式中,uα、uβ为定子电压分量；iα、iβ为定子电流分量；p为微分算子；Ld、Lq为d-q轴电感分量；R为定子电阻；Eα、Eβ为反电动势分量，且满足：

(2)

式中,ωe为电角速度；θe为电角度；ψf为永磁体磁链。

由式(2)可知，表贴式三相PMSM的反电动势与电机转子的位置角和转速有关。电机转速越大，反电动势也越大，反之亦然。因此，通过获取电机的反电动势，便可估算出电机转子位置角度、转速等信息。

2 无位置传感器PMSM控制算法设计

无位置传感器PMSM控制系统框图如图1所示。其无位置传感器控制算法采用本文所设计的自适应滑模观测器。

图1 PMSM控制系统框图

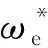
2.1 自适应滑模观测器设计

在PMSM数学模型中，将式(1)变形为：

(3)

本文采用的是表贴式PMSM，d-q轴电感分量Ld、Lq是相等的。因此，令Ls=Ld=Lq为d-q轴电感等效值。

传统滑模观测器采用sign符号函数构造观测方程，极易产生系统抖振。本论文采用sigmoid阈值函数构造观测方程，式(4)为sigmoid函数的定义式。

(4)

其中，a是一个正常数，其取值大小决定了sigmoid函数曲线收敛于±1的速度。在a>1的条件下，a的取值越大，sigmoid函数收敛速度越大，滑模控制系统的响应速度就越快。但也会导致函数边界层厚度减小，曲线特征就越接近sign函数，极易产生滑模抖振；反之，a取值越小，sigmoid函数边界层厚度越大，曲线就越平滑，产生的滑模抖振越小。但函数收敛速度也随之减小，从而影响滑模控制系统的动态性能。因此，为了保证滑模控制系统动态性能的同时降低滑模抖振，就需要选取合适的a值。本文选取的a值为20。

因此，根据式(3)电机定子电流状态方程，构造自适应滑模观测方程为：

(5)

(6)

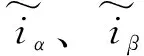
将式(5)减去式(3)，可得PMSM定子电流误差状态方程：

(7)

根据滑模面构造原则，构造滑模面函数为

(8)

当系统处于滑动模态时，式(9)成立。

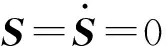
(9)

将式(9)代入式(7)可得电机反电动势的估计值：

(10)

为了使估计的反电动势更为光滑，本文提出了一个反电动势自适应估计环节替代传统的低通滤波器。通过引入自适应参数λ，设计合适的反电动势自适应律，从而降低锁相环对电机转子位置和转速的估计误差。

由于PMSM的电气时间常数很小，因此可以假设电机在一个周期内的加速度为零，即：

(11)

则对式(2)微分可得：

(12)

根据式(12)，设计如式(13)反电动势的自适应律。

(13)

其中，λ是一个正常数。λ取值过小，将会导致滑模观测器估计的反电动势波形失真，引起滑模控制系统震荡。反之，λ取值过大，则会增加系统的响应时间，从而影响滑模控制系统的动态性能。

根据式(11)和式(12)，将式(13)改写为

(14)

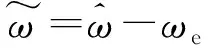
采用Lyapunov稳定性原理证明自适应滑模观测器的渐近稳定性。构造Lyapunov函数：

(15)

对式(15)求微分，并将式(14)代入可得：

(16)

由式(16)可知，自适应滑模观测器满足Lyapunov稳定性条件。因此，改进型滑模观测器能够实现电机反电动势的估计。

2.2 转子位置与转速的锁相环估计方法

本文采用锁相环技术实现电机转子位置和转速的估计，其原理框图如图2所示。

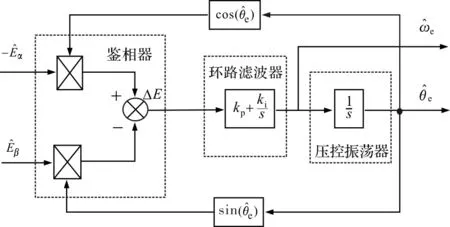
图2 转子位置与转速的锁相环估计框图

(17)

此时，图2的电机转子位置和转速估计框图可等效为

由图3可知，该估算系统的闭环传递函数为

图3 转子位置和转速估计等效结构图

(18)

误差传递函数为

(19)

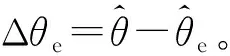
(20)

由式(20)可知，电机转子位置与转速的锁相环估计环节满足Lyapunov稳定性条件，即该锁相环可以实现电机转子位置和转速的准确估计。

3 仿真与实验验证

3.1 仿真验证

为了验证改进算法的估计性能，利用Matlab搭建PMSM仿真模型。选用规格为“36 V 200 W”的PMSM为被控对象，其具体参数详见表1。

表1 “36V 200W”PMSM参数

采用转速突变的情形来验证本文设计的算法。电机以额定转速3000 r/min的速度空载起动。在0.06 s时，电机转速突降为2500 r/min，观察改进型滑模观测器转子位置、转速的跟踪能力。自适应参数λ为800，滑模增益k为350，锁相环PI调节比例参数kp为3.5，积分参数ki为3。

本文将改进前后的滑模观测器的估计结果进行比较来分析算法的性能。首先分析反电动势的估计结果，其仿真波形如图4所示。仿真结果表明算法改进前后的反电动势估计波形都呈正弦规律变化。但是改进型算法与传统型相比，在0.06 s转速突变时，波形过渡更为平滑，且无毛刺现象。

图4 滑模观测器反电动势估计波形图

滑模观测器转速估计结果如图5所示，虚线是给定值，即电机转速输出；实线是估计值，即滑模观测器转速估计。由图5可知，两种观测器的转速估计都能很好地跟踪电机的转速输出，其调节时间约为0.01 s，但是传统滑模观测器的转速估计结果含有大量的谐波成份，系统抖振比较严重。在0.06 s转速突降时，传统滑模观测器有毛刺现象的出现，而自适应滑模观测器的估计结果比较平滑，进一步削弱了系统抖振问题。

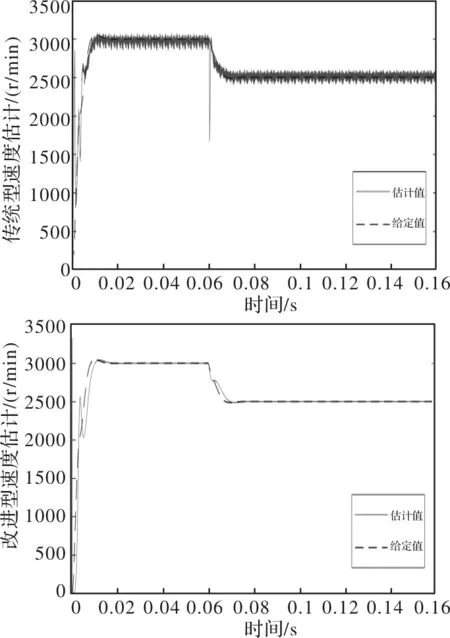
图5 滑模观测器转速估计波形图

为了分析电机转速的估计精度，将给定值与估计值做差得到电机转速估计误差波形如图6所示。数据处理可得，在电机转速2500 r/min下，传统型滑模观测器的转速估计稳态误差为97.28 r/min，改进后的自适应滑模观测器的转速估计稳态误差为4.67 r/min。改进型滑模观测器相对于传统型其转速估计精度提高了95.2%。

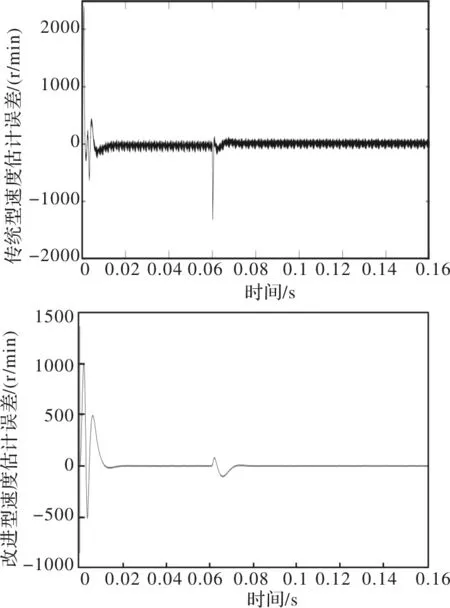
图6 滑模观测器转速估计误差波形图

图7为滑模观测器位置估计波形，虚线是给定值，即电机转子位置信息；实线是估计值，即转子位置估计。由图可知改进后的滑模观测器的位置估计抖振更小、更准确。

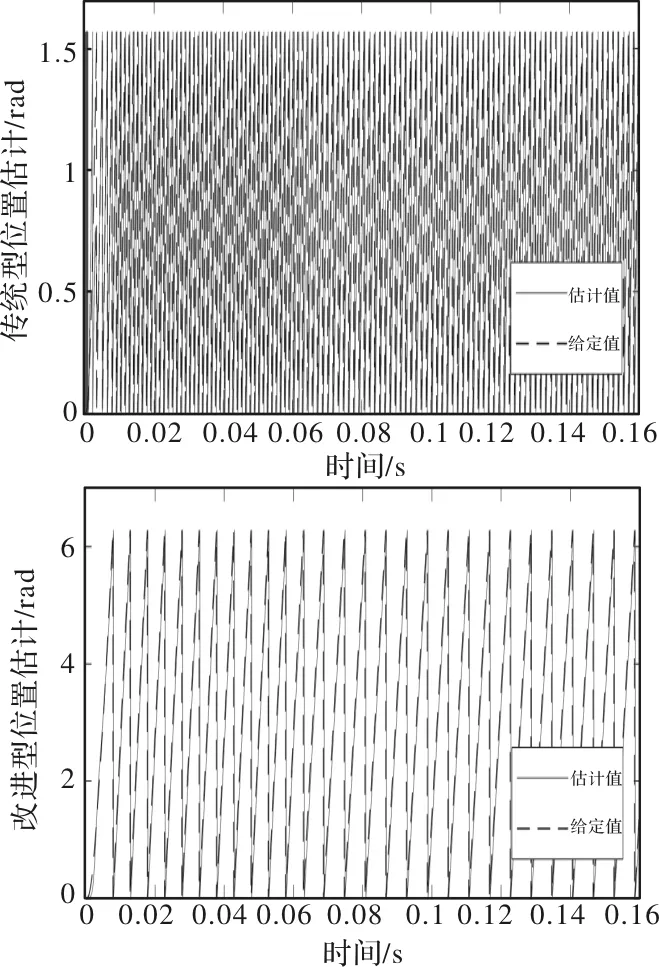
图7 滑模观测器位置估计波形图

为了进一步分析电机转子位置的估计精度，将给定值与估计值做差得到电机转子的位置估计误差波形如图8所示。在0.06 s转速突变时，位置估计误差出现了明显抖动。数据处理可得：在电机转速2500 r/min下，传统滑模观测器的位置估计稳态误差为0.327 rad，改进型滑模观测器的位置估计稳态误差为0.251 rad。改进型滑模观测器相对于传统型其位置估计精度提高了23.24%。分析结果与转速估计结果相一致，改进后算法能够提高滑模观测器观测精度。

图8 滑模观测器位置估计误差波形图

3.2 实验验证

为了进一步验证自适应滑模观测器的可行性，本论文以STM32F405为核心搭建如图9所示的PMSM控制平台。平台采用IR公司的F540N来驱动一台规格为“36 V 200 W”的正弦波PMSM。实验参数与仿真参数相同如表1所示。

图9 PMSM控制平台

为了验证自适应滑模观测器位置和转速估计的准确性，本文将该算法估计的转子位置和转速信息与光电编码器测得的数据进行比较分析。电机首先以额定转速3000 r/min空载起动。在3.8 s处转速突降为2500 r/min，电机转速波形如图10(a)所示。

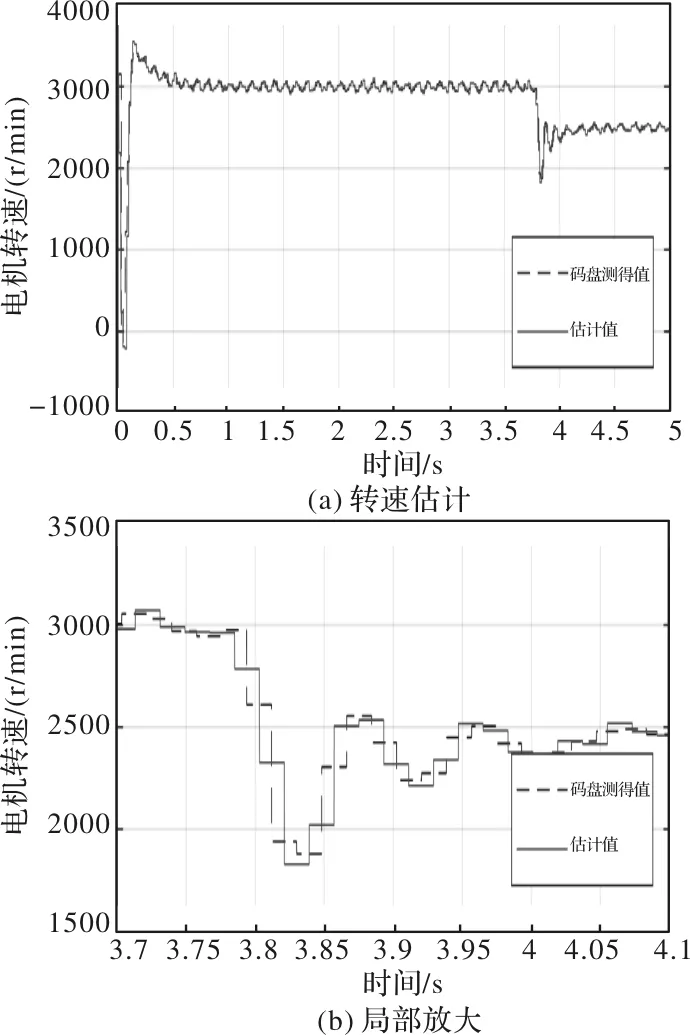
图10 自适应滑模观测器转速估计波形图

图中虚线表示的是光电编码器测得的转速波形，即码盘测得值；实线表示的是改进型滑模观测器转速估计波形，即估计值。将3.7～4.1 s的电机转速波形进行放大处理，如图10(b)所示。观察分析可得：改进型滑模观测器转速估计波形与光电编码器测得的转速波形契合度很高，具有很好的转速跟踪能力。

为了分析转速估计精度，将码盘测得值与估计值做差可得电机转速估计误差，如图11(a)所示。将其部分转速估计误差波形进行放大处理，如图11(b)所示。数据处理分析可得：在电机转速为额定转速3000 r/min下，改进型滑模观测器的转速估计稳态误差为79 r/min。

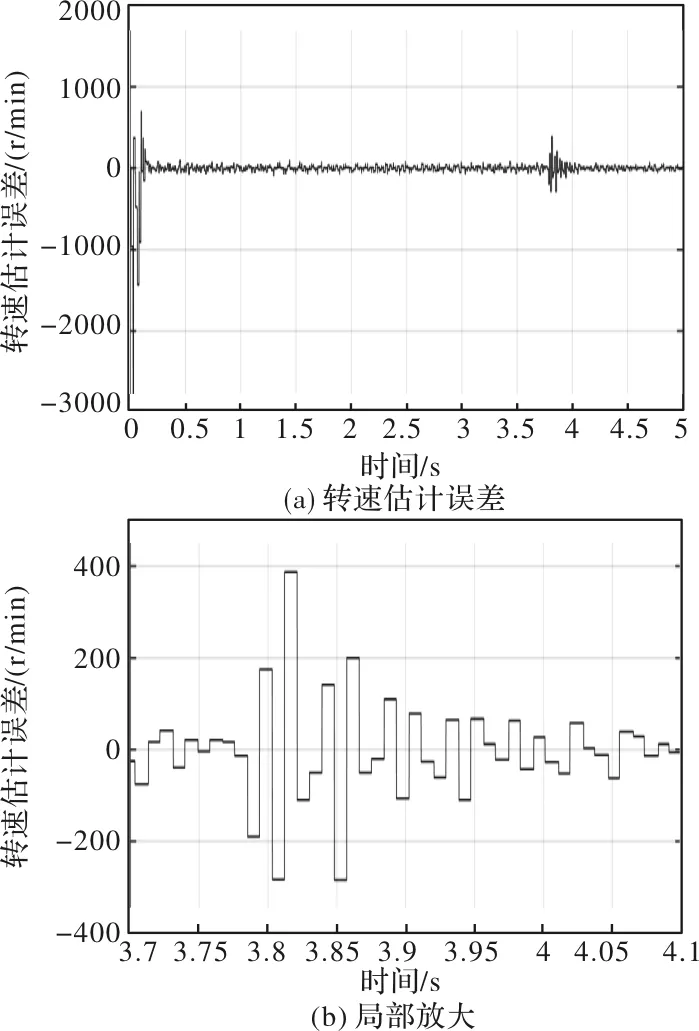
图11 自适应滑模观测器转速估计误差波形图

图12(a)为电机转子位置的波形图。图中虚线是由光电编码器直接测量的电机转子电角度，即码盘测得值。实线表示的是改进型滑模观测器对电机转子位置的估计波形，即估计值。由图12(b)可知，估计值与码盘测得值波形几乎重合。

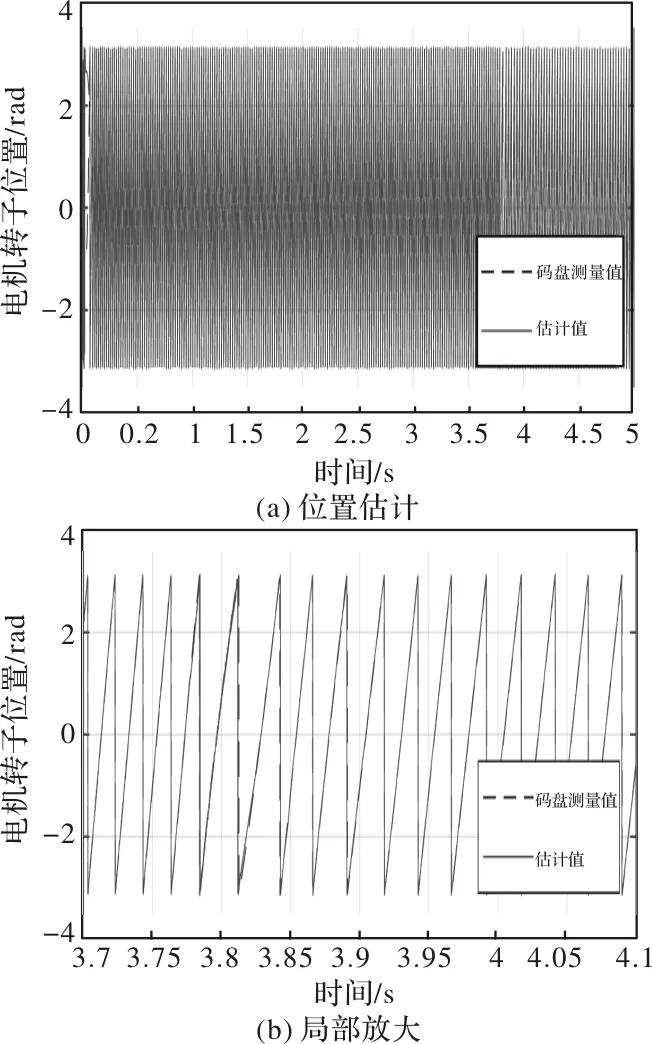
图12 自适应滑模观测器位置估计波形图

为了更好地分析改进型滑模观测器位置估计精度，将码盘测得值与估计值做差可得电机转子位置误差波形，如图13(a)所示。由图13(b)电机转子位置估计误差波形的局部放大图可知，电机在额定转速3000 r/min下，改进型滑模观测器的位置估计稳态误差为0.129 rad。综上所述，改进型滑模观测器可以实现无位置传感器PMSM高精度控制。

图13 自适应滑模观测器位置估计误差波形图

4 结 语

本文针对无位置传感器PMSM控制存在的转子位置与转速估计精度不高的问题，设计了一种新型的自适应滑模观测器。采用Sigmoid阈值函数代替sign符号函数，降低系统抖振；提出了一个反电动势自适应估计环节优化电机反电动势的估计值；采用锁相环技术实现转子位置和转速的高精度估计。根据Lyapunov稳定性原理，证明了本文所提控制策略的渐进稳定性。仿真与实验结果显示，改进型滑模观测器的反电动势估计值与传统相比更光滑，大大削弱了系统抖振；电机转子位置和转速都具有很好的跟踪性能，其稳态误差分别为0.129 rad、79 r/min。综上所述，改进型滑模观测器可以实现无位置传感器PMSM高精度控制。