“工字形”直线超声电机的结构设计与模态分析

张 健，王笑竹，何 勍，荆 珂

(1.营口理工学院,辽宁 营口 115014；2. 辽宁工业大学,辽宁 锦州 121001)

0 引 言

超声电机利用压电材料的逆压电效应，激发弹性体在超声频率范围内微幅振动，将这种微幅振动转换成动子的旋转或直线运动，来实现功率输出以达到驱动负载的目的[1]。超声电机不同于传统的电磁电机，它没有磁极绕组和磁路，不依靠电磁相互作用来转换能量，且无噪声、无电磁干扰、响应快，是一种可称之环保型动力源[2]。在航天、机器人、汽车、照相机、医疗器械、微电子机械等领域都已得到成功的应用[3]。

直线超声电机是超声电机领域的一个重要分支。以其结构简单，设计灵活、越来越得到人们的关注，在微型、直线运动装置的驱动和控制领域有着广阔的应用前景，已经成为国内外研究的热点之一。从20世纪80年代，国外一些学者和科研机构就开始了直线型超声电机的研究[4]，哈尔滨工业大学研制出一种基于夹心换能器式直线超声电机，驱动齿产生椭圆运动，推动导轨运动。电机在40N预紧力下，无负载速度480mm/s；纵振驱动电压120V，弯振驱动电压180V，预紧力110N，相位差60°时最大推力25N，最大速度为270mm/s。南京航空航天大学研制出一种纵、弯复合模态直线超声电机，两定子并联同时驱动时，弯振电压峰峰值为300V，纵振电压峰峰值为200V，频率为36.77kHz，最大推力为23N。清华大学研制了一种双振子型直线超声电机，由2个对称的摇头振子构成，驱动导轨直线运动。电机最大空载速度704mm/s，预压力为12.69N，电压峰峰值为226V时，驱动力为21N。上海大学研制出仿生步行小型直线超声电机，利用一组压电元件激振，激发出弹性体的绕X轴弯曲和绕Z轴扭转耦合振动模态。实现行走驱动。无负荷最大输出速度为0.08m/s，样机上可搭载的最大负荷为15N。

直线超声电机研究工作主要集中在高校、科研机构，所研究的电机在输出力、稳定性、实际应用等方面和国外相比还有一定的差距[5]。超声电机存在的性能不稳、效率低、负载特性难以预测、难以实现精确控制以及无法按照性能要求进行设计[6]。电机输出性能不高，与实际应用还有差距，目前实际应用的只能达10W左右[7]。

本论文在纵、弯复合模态直线超声电机的基础上，提出利用“工字形”金属弹性体两侧直梁的1阶伸缩模态和3阶弯曲模态叠加，交替拨动动子实现双向力的输出的一种直线驻波超声电机，对“工字形”弹性体的几种振动模态进行分析，完成“工字形”振子的结构设计，以纵、弯振动模态频率差最小为目标对振子进行了优化设计，确定振子的各结构参数；对原理样机进行测试分析，为后续超声电机的驱动控制做理论铺垫。

1 “工字形”弹性体的振动模态

“工字形”弹性体的振动模态驱动方案利用两侧直梁的3阶对称弯曲振动与1阶交替伸缩振动模态叠加形成复合振动模态，其驱动过程如图1所示，左侧直梁伸长的同时又做弯曲振动，两端部驱动点同时向左上(下)拨动动子，此时右侧直梁驱动点与动子脱离，弹性体振子相对动子向右运动；接下来两侧直梁恢复到初始状态，弹性体振子依靠惯性继续向右运动；下一过程右侧直梁做拉伸振动又做弯曲振动，两端部驱动点向左上(下)拨动动子。弹性体振子继续向右运动。图2所示，为两模态不同相位差所对应的驱动点运动轨迹，当0<φ<π时，椭圆运动轨迹为顺时针方向；当-π<φ<0时，椭圆运动轨迹为逆时针方向。当相位差变化φ=π/2，驱动点运动轨迹方向发生改变，振子反向驱动。反向驱动过程与正向过程类似。

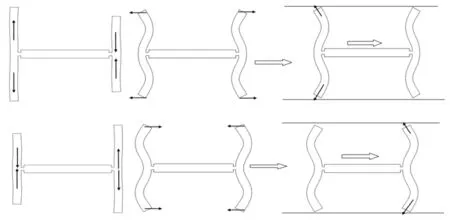
图1 3阶对称弯曲振动与1阶交替伸缩振动模态

图2 相位差与运动轨迹的关系

2 振子的结构及模态优化

根据振动理论中，梁弯曲振动固有频率与直梁的长度的关系与伸缩振动杆的长度与固有频率的关系，可推导出

(1)

(2)

式中，fB3为3阶弯曲振动固有频率；fL1为1阶伸缩振动固有频率；h为直梁的厚度；ρ为直梁单位体积的质量。

由式(1)和式(2)可知，振子两侧直梁的长度与振动模态的频率成反比，振子工作模态频率过高，压电陶瓷片容易发热，振动幅值变小，将影响电机性能。振子工作模态的频率过低，压电陶瓷片性能不易发挥。一般振子的工作频率在25kHz～55kHz之间。综合考虑，把振子的工作频率选在35kHz附近。

令两频率相等 ，整理得

(3)

振子的工作频率设为35kHz，

联立式(2)和式(3)得，l= 52mm，h= 4.675mm。

驱动齿不易过高，宽度不易过小否则影响刚度易断裂。综合各种因素，本文选择驱动齿尺寸选为齿高为1.5mm，厚度为2mm。

设计复合模态直线电机关键在于如何用同一频率电信号，同时激发出两工作模态。这需要对振子的结构进行优化。在Ansys中建立振子的有限元模型，通过调节振子结构尺寸参数，来完成对振子振动模态频率差最小化的动态设计。使振子的两工作模态满足：共振频率点接近(频率差最小)，即在两共振频率范围内用某一频率的电信号激励时两模态都能接近共振状态，振幅足够大。

振子结构的具体尺寸、陶瓷片的位置、柔性铰链及支撑结构的尺寸等都需要进一步优化才能获得。振子的工作模态如图3所示，图3(a)为伸缩振动模态，其固有频率为33.07kHz；图3(b)为弯曲振动模态，其固有频率为33.08kHz，频率差为8Hz。

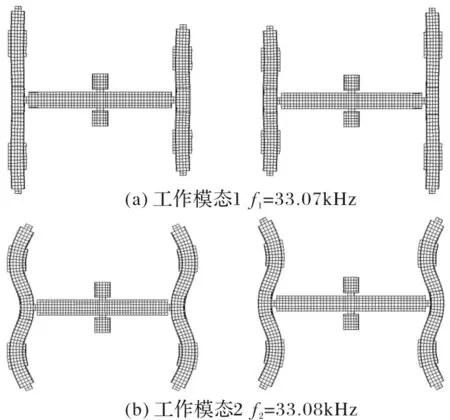
图3 振子的工作模态

2.1 工作模态的影响因素分析

根据振动理论，直梁长度和厚度对梁的纵、弯振动模态影响较大。弯曲模态近似线性变化且斜率较大，伸缩振动模态频率变化较平缓。横梁长度、厚度对伸缩振动模态几乎无影响，对弯曲振动模态影响严重。对电机会产生不利影响。由于支撑结构选在振动模态的节面处，支撑结构与振子之间的柔性铰链对模态影响很小。通过分析发现，此铰链尺寸变化时，频率差变化范围在几十赫兹。然而，纵横梁间的柔性铰链对振子的两模态的影响较为敏感。超出柔性铰链尺寸变化范围，弯曲模态振型有明显变化(纵向有位移变化)，会导致电机无法工作。因此柔性铰链长度的变化对伸缩振动模态几乎无影响，对弯曲振动模态的频率影响较大。

2.2 振子的刚度分析

由于直线超声电机是通过振子驱动齿拨动动子滑块做直线运动的，振子的柔性铰链、驱动齿部位往往是主要受力部位，而且结构比较薄弱。因此，有必要对振子的驱动齿、柔性铰链部位进行静力学分析，分析各节点位移对力载荷响应情况，即振子的刚度分析。由于振子两侧直梁是交替工作的。因此，在振子的单侧直梁两驱动齿端部x轴方向(与动子运动方向反向)施加力载荷F，观察柔性铰链、驱动齿各节点x轴向位移变化。

在柔性铰链、驱动齿上取四个节点A、B、C、D在振子两侧驱动齿施加力载荷F，观察节点x轴向位移变化。图4为振子在力载荷作用下各节点位移变化云图，可以看出，驱动齿端部位移变化最大。

图4 振子在力载荷作用下应变云图

图5为各节点刚度曲线，曲线的斜率为各节点的刚度。图5(a)为柔性铰链处A、B、C点刚度曲线，从曲线斜率可知，各节点的位移变形量随着施加的力的增加而增大，其中A点刚度最大12 N/μm，B点刚度最小为3.7N/μm。图5(b)为驱动齿D节点刚度曲线，刚度为0.074N/μm。

图5 各节点刚度曲线

3 样机的实验研究

根据振子结构优化结果，加工试制了原理样机，如图6所示。把电机固定在实验平台上(图7)，用细绳将动子滑块上的销钉经过测试支架与重物(砝码)连接，动子正、反方向运动带动重物运动。

图6 原理样机

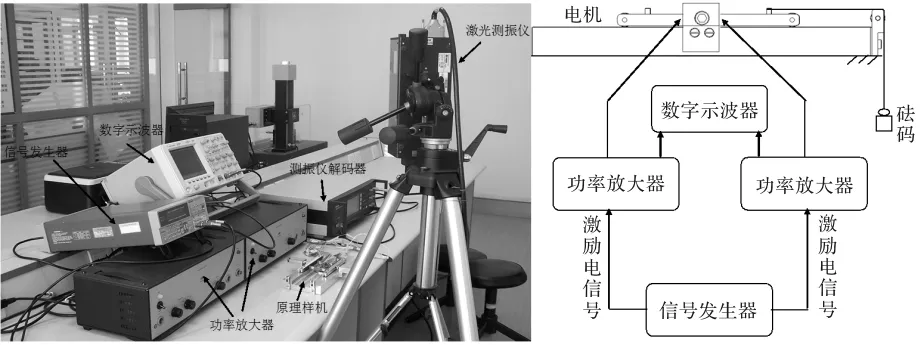
图7 实验测试平台

模态测试时将频率设定在Ansys模态分析结果的数值上，在其附近进行微调，通过扫描两侧纵向直梁的侧面来确定弯曲模态的振型及共振频率。实验测得振子的两工作模态的共振频率的频率差为200Hz，在30.60kHz与30.80kHz范围之间的某个频率值能使振子的两个振动模态同时接近共振状态。

如图8所示，将振子工作模态的谐振频率与有限元法计算得到的固有频率进行对比，可知，振子的实测谐振频率与有限元计算的数据有一定的偏差。实测的频率值比有限元计算值要低，其原因是在测试时振子的边界条件与有限元计算时相比发生了变化。另外，利用有限元分析软件对振子进行模态分析以及结构优化时，有限单元网格的大小以及材料属性参数与实际材料属性之间有偏差，另外，压电陶瓷片与弹性体之间黏结层的等因素都对振子的谐振频率产生影响，导致了计算结果与实测数据之间有一定的偏差。

图8 振子幅频特性曲线

3.1 振幅分布情况测试

伸缩振动模态驱动齿质点纵向振幅和弯曲模态驱动齿质点横向振幅对振子的输出推力及驱动速度均有很大的影响。

图9为伸缩振动模态、弯曲振动模态驱动齿质点纵向振幅与激励电压的关系曲线，从图中可以看出两模态的振幅都随激励电压的升高而增大，但振幅增到一定值，趋于平稳。需要合理选择激励电压，若激励电压过低振幅就会偏小，压电陶瓷片性能不易发挥；若激励电压过大，振子的振幅过高，压电陶瓷片发热严重容易损坏。但是，从两幅图对比来看两模态激励电压不均衡，若想达到同一振幅，伸缩振动模态所需的激振电压要高。这是由于激励两工作模态的压电陶瓷片数量不均造成的，这一问题在实验中可通过调整两路电信号激励的压电陶瓷片数量来解决。图10所示，分别为在电压峰峰值为40V激振频率为30.88kHz，激励压电陶瓷片时1号直梁和2号直梁测试点振幅分布曲线，从图中可知有四个节点(位移为零)三个峰(谷)值点和两个振幅极值点(驱动齿端面上的点)。

图9 振幅与电压的关系

图10 直梁测试点振幅分布曲线

3.2 样机的输出性能研究

通常，直线超声电机是在振子工作模态谐振频率附近工作的。测试时将频率设定在Ansys模态分析结果的数值上，在其附近进行微调，通过扫描两侧纵向直梁的侧面来确定弯曲模态的振型及共振频率。实验测得：样机的工作频率在30.76kHz附近时动子正反向灵活运动，输出性能最优。图11所示为振子在小预紧力、驱动单侧滑块时激励电压与速度关系曲线。可知，速度变化与驱动电压成正比，当驱动电压最大值为238V时，电机动子Vmax=240mm/s。当驱动电压最大值为119V时，单侧滑块获得正反方向相同的速度。

图11 电压与速度关系曲线

在动子滑块销钉上吊砝码加负载测试，图12为预紧力为1.28N时激励电压和负载关系曲线。负载随着电压的增加而增加，当电压峰峰值为300V时，单侧动子滑块单向最大输出力为0.5N。

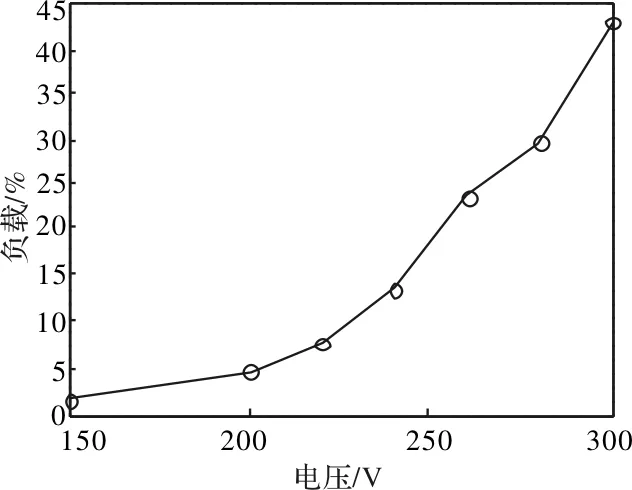
图12 电压与负载关系曲线

电机振子是依靠摩擦力驱动动子滑块运动的，预紧力越大动子所获得的摩擦力越大。但是，预紧力过大，不仅影响振子的工作模态，而且，影响振子切向驱动速度。图13为激励电压峰峰值为250V，负载为20g时，预紧力与动子运动速度的关系曲线，可见随着所施加的预紧力的增加，动子滑块的运动速度先增加然后下降，而且变化趋势较为明显。因此，预紧力对电机的输出性能有重要的影响，在一定范围内，适度的预紧力可增加振子的驱动速度，若预紧力过大将影响振子驱动速度。

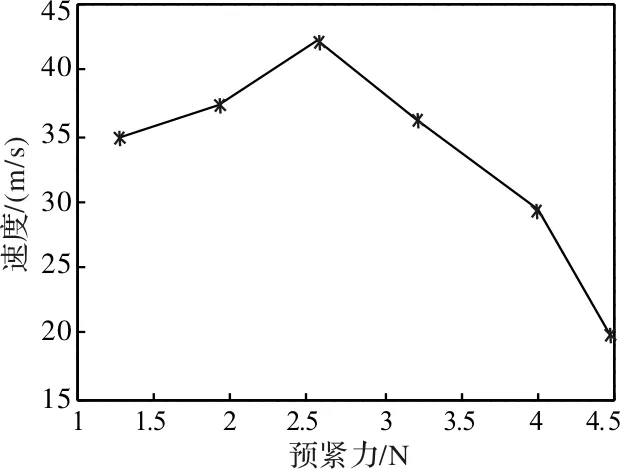
图13 预紧力与速度关系曲线

图14所示，施加2.5N的预紧力，激励电压峰峰值250V，对电机两侧滑块加载时，其速度与载荷关系图。从图中可知，载荷与速度间成反比。正、反两方向曲线不吻合。这说明电机的正反方向性能不同。产生这种现象的原因是两侧驱动齿与动子滑块摩擦材料的接触状况不同以及两侧预紧力调节的程度不一致所造成的。

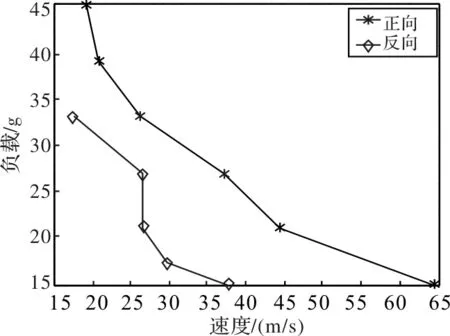
图14 速度与负载关系曲线(载荷与速度关系)

4 结 论

本文在纵、弯复合模态直线超声电机的基础上，提出并试制了一种新型的直线超声电机。通过改变两模态激励电信号相位差实现动子的正、反方向运动。利用Ansys软件对振子进行了结构动态设计，使两模态频率差最小。从而，达到利用同一驱动电源驱动，简化驱动电路设计的目的。

(1)提出了一种“工字形”振子结构，并对“工字形”弹性体的复合振动模态及其驱动方案进行了分析，选定了一种基于其两侧直梁的1阶交替伸缩和3阶对称弯曲复合振动模态作为样机的工作模态。

(2)对“工字形”压电振子进行了结构优化设计。以纵、弯振动模态频率差最小为目标对振子进行了优化，确定了振子的各结构参数。分析表明，中间横梁、纵横梁之间的柔性铰链尺寸参数对模态影响较为敏感。

(3)对振子以及原理样机进行测试。样机在两个谐振频率之间的30.76 kHz的频率驱动下，动子输出性能最优。