异步起动永磁同步电动机电磁振动特性及抑制措施的研究

唐 旭，林旭梅，朱文杰

(青岛理工大学 信息与控制工程学院，山东 青岛 266525)

0 引 言

电机的振动噪声主要分为三类：电磁噪声、机械噪声、空气动力噪声，其中，电磁噪声是电机振动噪声的主要来源。电磁噪声是由电磁振动引起的，而电磁振动则是由不断变化的电磁力作用于定子铁心所激发的。与传统的电励磁电机相比，永磁电机中永磁体产生的气隙磁密分布接近矩形，含有大量的谐波，这使得永磁电机的电磁振动通常比同规格的电励磁电机严重得多。

文献[1]基于气隙磁密的计算推导了表面式永磁电机电磁力的解析表达式，文献[2-3]利用电磁及结构有限元法计算了表面式及普通内置式等单边开槽永磁电机的电磁振动噪声，文献[4-6]研究了通过定子辅助槽、偏心磁极、改变定子齿形状等方法抑制表面式永磁电机的电磁振动，文献[7]研究了通过在定子绕组中注入补偿电流抑制永磁电机的电磁振动，文献[8]研究通过软件算法削弱永磁电机控制系统中由死区、电流采样失真而产生的振动噪声。

与表面式及普通内置式等单边开槽永磁电机相比，异步起动永磁同步电动机定转子双边开槽，电机运行时，作用于定子铁心的电磁力的分布更加复杂，难以直接采用单边开槽永磁电机的电磁振动分析方法及抑制措施。文献[9]利用有限元法计算了异步起动永磁同步电动机的电磁力分布，并进行了模态分析，计算了电磁力作用下的振动幅值；文献[10]则基于电机振动噪声信号的提取、分析，进行了异步起动永磁同步电动机的故障诊断。可以看出，目前针对异步起动永磁同步电动机电磁振动的研究尚不多见，并且尚未有文献研究该类电机电磁振动的有效抑制措施。

本文提出了一种解析分析异步起动永磁同步电动机负载运行时电磁力的方法，该方法可以建立不同阶数、频率的电磁力与电机主要结构参数之间的明晰关系；在此基础之上，本文研究了通过改变定子齿宽抑制异步起动永磁同步电动机的电磁振动，得到了相应的定子齿宽确定方法。以一台1.5kW、4极异步起动永磁同步电动机为例，利用有限元法验证了上述电磁振动抑制措施的有效性。

1 异步起动永磁同步电动机电磁力的解析分析

本文研究的是采用串联式磁路结构的异步起动永磁同步电动机，其定转子铁心冲片结构如图1所示，采用其他磁路结构的异步起动永磁同步电动机电磁振动的分析方法与之类似。

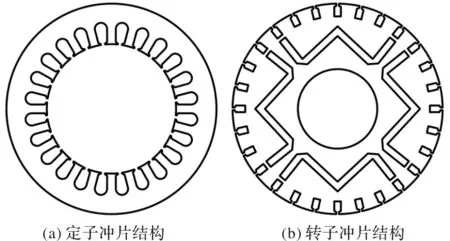
图1 本文研究的异步起动永磁同步电动机定转子冲片结构

根据麦克斯韦张量法，作用于定子铁心内表面的径向电磁力密度可以表示为

(1)

式中，θ为气隙圆周角，μ0为空气磁导率，Br(θ,t)为径向气隙磁密分布，Bt(θ,t)为切向气隙磁密分布。为了便于计算，假设定转子铁心的磁导率无穷大；与径向气隙磁密相比，电机的切向气隙磁密忽略不计。

电机的径向气隙磁密分布可以表示为

(2)

式中，F(θ,t)为定子绕组磁动势Fs(θ,t)、转子永磁体磁动势FPM(θ,t)的合成磁动势，δe为考虑定转子铁心双边开槽时的等效气隙长度，λs(θ)、λr(θ,t)分别为定子齿槽、转子齿槽对应的相对气隙磁导函数。

将式(2)代入式(1)可得

(3)

因此，在分别求得相应的定子绕组与转子永磁体磁动势、定转子齿槽对应的相对气隙磁导函数的傅里叶展开式之后，就可以得到电机径向电磁力密度分布的解析表达式。

(1)永磁体磁动势FPM(θ,t)的相关傅里叶展开式

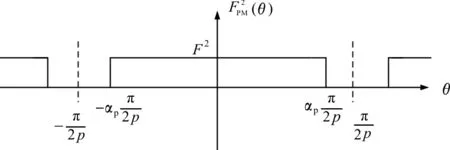
t=0时刻，转子内置永磁体产生的空间磁动势分布FPM(θ)如图2所示。其中，θ=0的位置设置在某一指定永磁磁极的中心线上，p为电机的极对数，αp为永磁磁极的极弧系数，F为永磁体磁动势的幅值。本文所提出的电磁力解析分析方法目的不在于电磁力的准确计算，因此并未给出F的具体值。

图2 FPM(θ)的分布

FPM(θ)的傅里叶展开式为

FPM(θ)=∑Fμ1cos(μ1pθ)

(4)

式中，μ1=1,3,5,…，转子旋转时，对应的FPM(θ,t)的傅里叶展开式为

FPM(θ,t)=∑Fμ1cos(μ1ωt-μ1pθ)

(5)

式中，ω为电机旋转的电角速度。

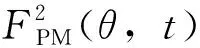
图的分布

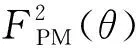
(6)

式中，μ2=1,2,3,…。

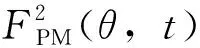
(7)

(2)定子绕组磁动势Fs(θ,t)的傅里叶展开式

不考虑t=0时刻定子A相绕组轴线与指定永磁磁极中心线之间的夹角，假设电机三相对称电流按照正弦波规律变化，且t=0时刻定子A相绕组电流达到最大值时，三相合成的空间磁动势基波及各次谐波分布可表示为

(8)

考虑t=0时刻A相绕组轴线与指定永磁磁极中心线之间的空间夹角φ时，Fs(θ,t)可表示为

Fs(θ,t)=∑Fvcos(ωt-vpθ+vpφ)

(9)

式中，v=6m+1，m=…,-3,-2,-1,0,1,2,3,…。

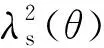
图的分布

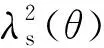
(10)

式中，k1=1,2,3,…。

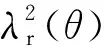
图的分布

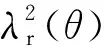
(11)

式中，k2=1,2,3,…。

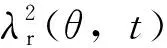
(12)

将式(5)、式(7)、式(9)、式(10)、式(12)代入式(3)，可以得到异步起动永磁同步电动机的电磁力解析表达式，按照产生电磁力的磁动势来源可分为三类，进一步整理可得电磁力的阶数、频率成分，如表1所示，其中，f为电源频率。

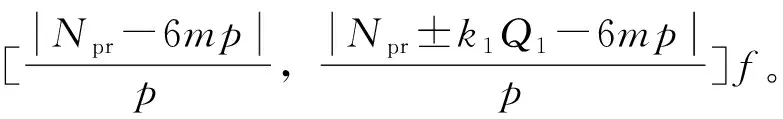
2 异步起动永磁同步电动机的电磁振动响应分析

2.1 电磁力的有限元计算分析

本文研究所采用的样机是一台1.5 kW、4极异步起动永磁同步电动机，其定转子冲片如图1所示，主要参数如表2所示。

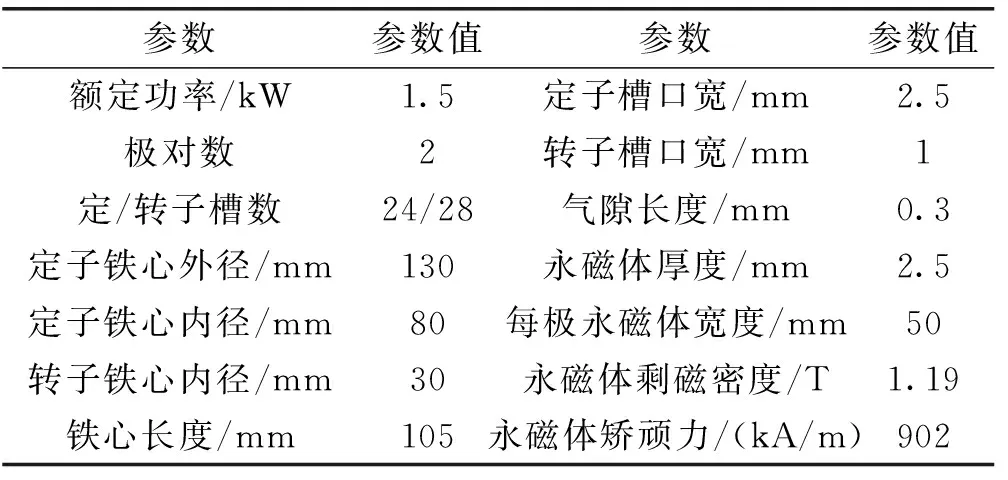
表2 样机的主要参数

利用有限元法计算得到的样机带额定负载转矩稳定运行时，某一瞬间的径向电磁力密度沿气隙圆周的分布如图6所示，其傅里叶分解结果如图7所示。可以看出，样机电磁力的最小阶数为4，主要阶数为4的整数倍。

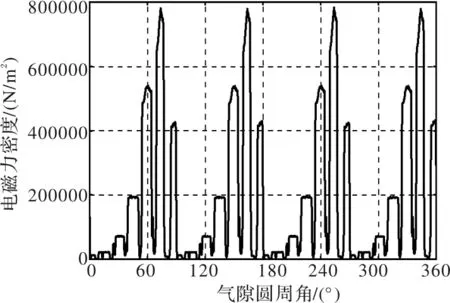
图6 样机的径向电磁力密度分布

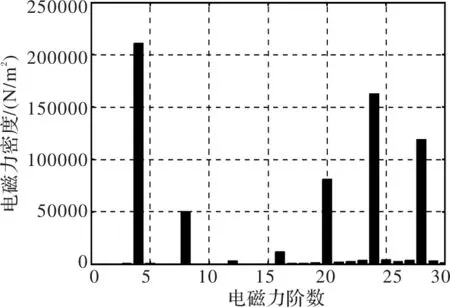
图7 样机径向电磁力密度分布的傅里叶分解结果

根据表1，可以得到电机电磁力的最小阶数为GCD(2p,Q1)，主要阶数为GCD(2p,Q1)的整数倍；对于样机，可以计算其电磁力的最小阶数为4，主要阶数为4的整数倍，与有限元计算结果相吻合。

径向电磁力引起的振动噪声不仅与电磁力的幅值有关，还与电磁力的阶数Npr有关，一般只考虑Npr≤4的电磁力；对于样机，只需考虑4阶电磁力。

样机带额定负载转矩稳定运行时，利用有限元法计算得到的某一定子齿顶的固定位置处4阶电磁力的变化曲线，如图8所示，对其作傅里叶分解，可以得到4阶电磁力中不同频率成分的幅值，如图9所示；可以看出，4阶电磁力的主要频率成分包括[2,4,8,10,14,16,22,26,…]f。根据表1，可以计算样机4阶电磁力的主要谐波次数为6k-2、6k-4 (k=1,2,3,…)，与有限元计算结果相吻合。

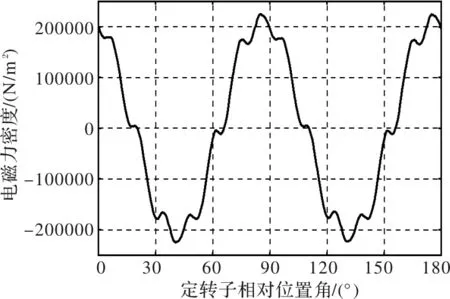
图8 定子齿顶处4阶电磁力的变化曲线

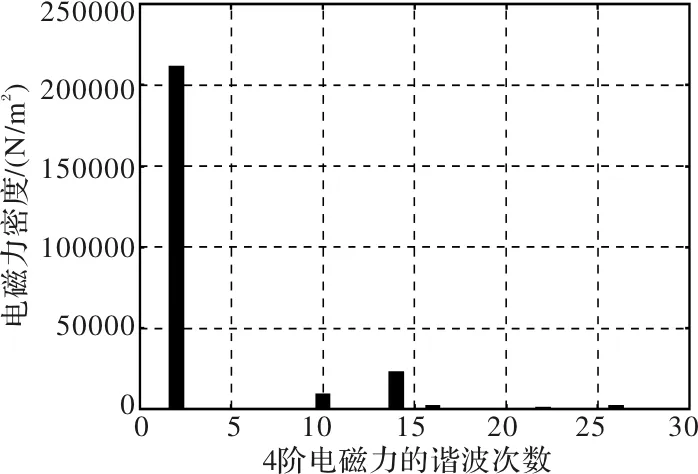
图9 4阶电磁力变化曲线的傅里叶分解结果

从上述分析可以看出，利用本文提出的分析方法得到的异步起动永磁同步电动机径向电磁力的解析表达式，可以准确反映电磁力的主要阶数及频率成分，可用于进一步研究电磁振动的抑制措施。

2.2 电磁振动噪声的机械阻抗分析模型

根据文献[4]中电磁振动噪声的机械阻抗分析模型，当幅值为Pr的Npr阶电磁力作用于定子铁心内表面时，等效的集中力为

Pre=2πRi1l1Pr

(13)

式中，Ri1为定子铁心的内半径，l1为定子铁心的轴向长度。

该集中力作用于定子铁心和机壳时，引起的振动位移为

(14)

式中，K1、K2分别为定子铁心和机壳的刚度，m1、m2分别为定子铁心和机壳的等效质量，ωr为Npr阶电磁力的角频率。

产生的辐射声功率为

(15)

式中，ρ0、c0分别为空气的密度和声波在空气中的传播速度，Sf为声辐射模型的表面积。对应的声功率级为

(16)

不同频率的噪声产生的合成声功率级为

(17)

根据有限元法计算得到的4阶电磁力各次谐波的幅值，利用电磁振动噪声的机械阻抗分析模型，可以计算样机4阶电磁力产生的电磁振动噪声频谱，如图10所示。可以看出，幅值最大的声功率级出现在4900Hz(98次谐波)处。根据式(14)可以得到电机Npr阶振动模态的固有频率为

(18)

根据式(18)可以得到样机4阶振动模态的固有频率为4876.3Hz，4阶电磁力98次谐波的频率(4900Hz)与之接近，较小的电磁力就能引起较大的电磁振动噪声。因此，对于样机而言，4阶电磁力的98次谐波就是需要抑制的对象。

利用式(17)可以得到图10所示电磁振动噪声频谱的合成声功率级为75.03dB；另外，通过对图8所示的4阶电磁力变化曲线作傅里叶分解，可以得到其98次谐波的幅值为239.27N/m2。

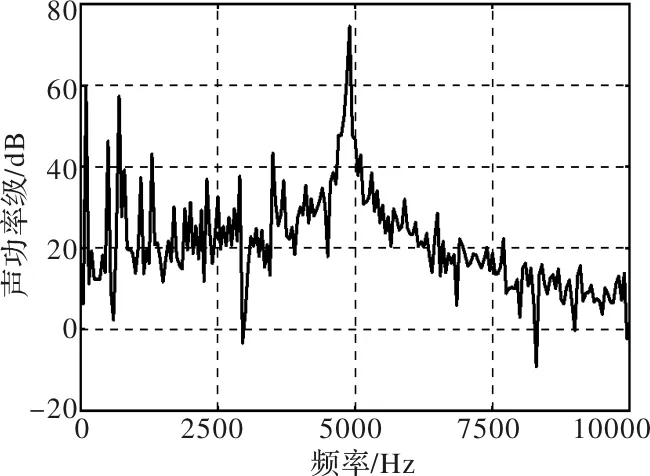
图10 样机的电磁振动噪声频谱

3 异步起动永磁同步电动机电磁振动的抑制

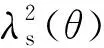
(19)

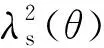
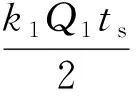
(20)

即能有效抑制电机电磁振动的定子齿宽为

(21)

式中，k=1,2,3,…。

分析表1可知，产生4阶电磁力的98次谐波、与Gk1相关的来源包括：

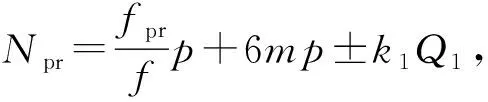
综上，对样机电磁振动起主要作用的电磁力项满足

(22)

由2.2节可知，对表2所示样机的电磁振动起主要作用的是4阶电磁力的98次谐波。将Npr=4、fpr/f=98代入式(22)，可得产生4阶电磁力98次谐波的定子齿槽相对气隙磁导函数谐波次数为k1=8，代入式(21)可得能有效抑制样机电磁振动的定子齿宽为ts=11.25°(原定子齿宽为11.42°)，此时样机带额定负载转矩稳定运行，相应的4阶电磁力产生的电磁振动噪声频谱如图11所示。此时，样机的合成声功率级为73.37dB，相比原模型降低了1.66dB；同时，改变定子齿宽后，4阶电磁力98次谐波的幅值为187.48N/(m2)，减小了21.65%。

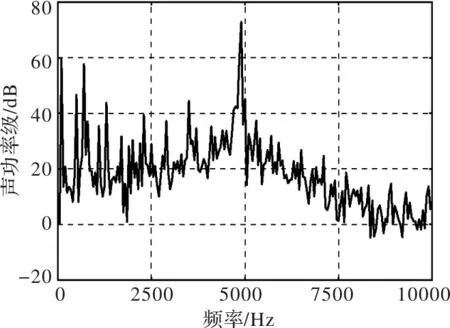
图11 样机改变定子齿宽后的电磁振动噪声频谱

4 结 论

本文针对异步起动永磁同步电动机定转子双边开槽、转子铁心内置永磁体，导致其电磁力成分复杂、解析计算难度大这一关键难点问题，提出了一种新的电磁力解析分析方法，建立了不同阶数、频率的电磁力与电机定转子齿槽参数之间的关系，并据此研究了通过优化定子齿宽抑制该类电机负载运行时的电磁振动；以一台1.5kW、4极异步起动永磁同步电动机为样机，利用有限元法验证了上述抑制措施的有效性，同时证明了本文提出的电磁力解析分析方法的有效性。