双能X射线高动态范围安检图像压缩算法

原培新， 陈鼎夫

(东北大学 机械工程与自动化学院， 辽宁 沈阳 110819)

X射线检测在国家公共安防领域扮演着特别重要的角色.它通过透射的方法扫描旅客的行李物品，并生成透照图像使安检人员可以在不打开旅客个人物品时查看是否携带违禁物.

现今安检最常用的是双能X射线检测系统.它通过产生高能与低能两种不同能量的射线对同一物品进行扫描，生成高、低能两幅图像，并各自包含部分微小细节，因此须同时对它们进行处理[1].

X射线安检图像噪声大、细节丰富，但最主要的问题在于其扫描出来的数据为16位数据，具有较高的动态范围，但高动态范围显示器的造价成本昂贵，应用于安检设备性价比较低.若要将高动态范围的图像直接显示在普通显示器上，则需要进行动态范围的压缩，降低检测数据的位数，这势必会导致数据信息的丢失，使显示出来的图像丢失部分细节.同时，由于安检图像的对比度较低，图像在黑暗区域、高亮区域以及物体重合区域显示不清，增加了安检人员的工作难度.因此，在压缩X射线图像动态范围的同时，如何增强图像细节信息、提高对比度是目前所需解决的重点.本文提出了一种基于多尺度局部保边(local edge-preserving,LEP)滤波的自适应色调映射算法以解决以上问题.

1 双能X射线的色调映射算法

现今对X射线图像的动态范围压缩以及图像增强的研究主要集中于工业探测领域以及医疗医学领域[2]，而对X射线安检图像的处理研究较少.

常见的色调映射算法有线性压缩法、对数函数压缩法、梯度压缩法[3]、基于双边滤波法等.线性压缩法是将图像每个像素点的灰度值线性缩小至原来的1/256，但这样做会造成对比度降低，灰度过于集中；对数函数压缩法能够保持图像的整体明亮效果，但会丢失大量细节信息；梯度压缩法在处理完图像之后，还需要进行泊松方程的求解，较为费时，不适用于安检这种比较注重实时性的领域.

基于双边滤波[4]的算法以及基于指导滤波、基于加权最小二乘滤波[5]的算法都与本文算法有相似之处，它们都是通过滤波将原图像分解为基础层与细节层，不足之处在于双边滤波算法处理后会引起边缘过度锐化，造成梯度反转且会出现“阶梯效应”；指导滤波算法不能很好地保持边缘，而加权最小二乘滤波算法的平滑效果较好，但对细节的提取较弱.

本文综合上述问题，采用局部边缘保持滤波，同时对高、低能图像进行多尺度滤波，分别得到1个基础层以及3个细节层；对细节层进行自适应的增强，对基础层进行自适应对数压缩，并将处理后的各层图像合并，进行直方图调整.最后将高、低能图像融合得到细节清晰、对比度高、噪声小的低动态范围双能X射线安检图像，具体算法流程如图1所示.

1.1 图像预处理

首先分别将安检机检测到的高、低能数据代入至算法中，由于检测数据为16位数据，数据范围为[0,65 535]，因此首先对数据进行归一化处理，处理公式为

I=Iin/maxIin.

(1)

式中：Iin代表输入图像的灰度值；maxIin代表输入图像灰度值的最大值；I代表归一化处理后的灰度值.

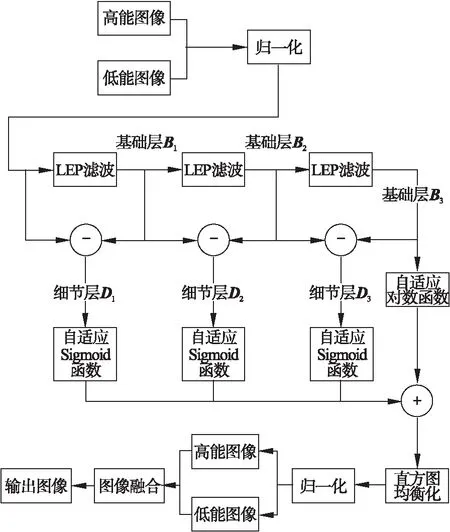
图1 算法流程图

1.2 局部保边(LEP)滤波

局部保边(LEP)滤波[6]与加权最小二乘滤波的想法一致，都希望滤波后的图像在具有较大梯度区域以外的区域能够尽可能平滑，同时使处理后的图像与原图像接近一致.但局部边缘保持滤波对显著边缘的定义不同，它认为显著边缘不仅仅是全局大梯度区域，在局部具有相对较大梯度的部分也被归为图像的显著边缘，因此在LEP滤波中，具有局部较大梯度的区域也被分解至基础层.

局部边缘保持滤波可以简单理解为求式(2)的最小值：

(2)

式中：Bi,j表示输出图像的(i,j)像素点的灰度；Ii，j为输入图像(i,j)像素点的灰度；w为滤波窗口；Ii，j表示(i,j)像素点处I的梯度；Bi,j表示(i,j)像素点处B的梯度；α为可调节参数，β用于调节梯度敏感度.对输入图像进行局部滤波以保留局部边缘.

受指导滤波[7]的启发，LEP滤波认为，在滤波过程中输入与输出图像呈线性关系，因此有

Bi，j=awIi,j+bw,(i,j)∈w.

(3)

联立式(2)与式(3)并求偏导可得

(4)

在每一个滤波窗口w中都含有N个像素，而每个像素又会被N个窗口所包含.每一个窗口都会有一组aw，bw，因此对输出Bi来说，也会有N种结果，对这N种结果取均值即可得到输出.

(5)

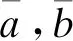
1.3 多尺度分解

图像多尺度分解是将图像经滤波器滤波后分解为一个基础层以及多个细节层的过程.

常用的多尺度分解方法分为两种:第一种为对原始输入图像进行多次滤波，每次选择不同大小的滤波窗口，之后对每次滤波后的细节层进行处理并最终将它们融合；第二种方法是对原始图像进行迭代地滤波分解，即每次都是对上一次滤波后输出的基础层进行再次滤波，并依次增大滤波窗口.两种方法都能够得到一系列逐步平滑的图像，但针对安检图像，第一种方法的效果并不明显，且易出现拼接痕迹，因此本文选择迭代分解法.

对原始输入图像进行一次LEP滤波后可得到一个输出图像，即为基础层，将输入图像与输出图像作差可得一个细节层.基础层保留着原始图像的局部均值以及局部突出边缘，而细节层包含着在零梯度周围震荡的信号.迭代地使用滤波器对图像进行滤波分解并依次增大滤波半径可得一个基础层以及多个细节层，实验表明：进行3次迭代滤波后可近乎完全提取图像细节，且运行时间较短，因此将滤波尺度定为3，具体表达式如下：

Bl=Ll(Bl-1),

(6)

Dl=Bl-Bl-1，

(7)

Iout=B3+D1+D2+D3.

(8)

式中Bl,Dl,Iout分别代表基础层、细节层和输出图像，B0为原始输入图像；Ll代表滤波函数；l代表滤波次数，l=1～3.

1.4 细节层自适应增强

在图像多尺度分解以后，需要对不同尺度下得到的细节层进行增强，提升对比度，从而达到增强图像细节信息的目的.

由于细节层包含许多在零梯度周围震荡的信息，因此希望找到一个函数，能够压缩远离0的较大值，同时增强较小值.此外，这样的增强函数还应使图像中每一点的偏离大致相等，且为了避免梯度反转，增强函数还应为凸函数，并关于原点对称.

满足上述条件的函数有Sigmoid函数[8]，如式(9)所示：

(9)

其形状大致如图2所示.

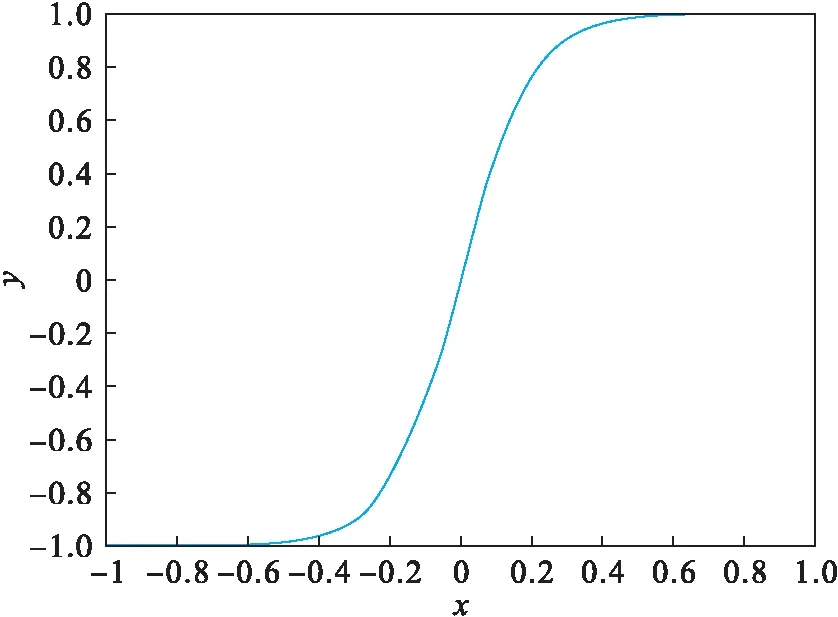
图2 Sigmoid函数

一般的Sigmoid函数都能够增强细节层，但是一些残留在细节层里的强边缘也会随着细节的增强而增强，当它们与基础层相加后就会引起较强的光晕现象，因此本文在Sigmoid函数里加入了梯度项，用来控制较大梯度的强边缘带来的影响，改进函数如下：

(10)

本文算法应用式(10)对图像的细节层进行增强，同时能够尽可能避免光晕的出现.

1.5 基础层对数自适应压缩

本文算法对3次迭代后得到的基础层采用自适应对数函数进行动态范围的调整，原因在于对数函数符合人眼对物体亮度的感知，同时，物质对X射线能量的衰减呈指数形式，因此在对数域上操作能够得到更好的表现.

Stockham于1972年首次提出应用对数函数对图像的亮度进行调整[9]，但其算法由于设置了一个固定的对数基底，无法同时对黑暗及高亮区域进行有效调整.Drago等提出了一种自适应对数色调映射算法[10]，它可以根据输入图像各点像素亮度值的不同，自适应地调整对数基底，具体变换公式如下：

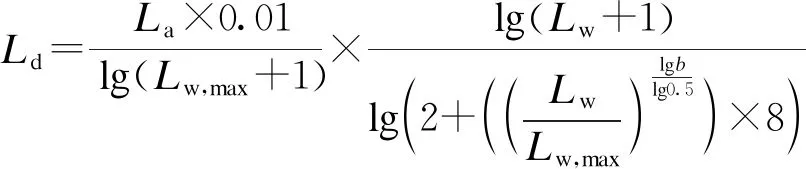
(11)

式中：Lw为输入图像各点亮度值；Lw,max为最大亮度值；La为一比例因子，用于调整输出图像的亮度，这里取La=100 cd/m2；偏置函数b(x)用于自适应调整对数基底：

(12)

式中：b为一关键系数，用于压缩高亮区域值并增强黑暗区域细节的可见度，实验表明b的取值在0.7～0.9之间时，大部分图像都能够取得较好效果，这里取b=0.8.

1.6 直方图均衡化

在X射线安检图像产生以及处理过程中，必然会产生噪声，因此应该进行直方图均衡化[11]调

整.本文算法对经过上述处理后的图像的灰度级前后各0.5%进行调整并对调整后图像进行归一化操作，以减少噪声对图像的影响，同时提升主要像素的对比度.以工具箱为例，处理前后的效果如图3所示；直方图的对比如图4所示.

图3 直方图均衡处理前后效果对比

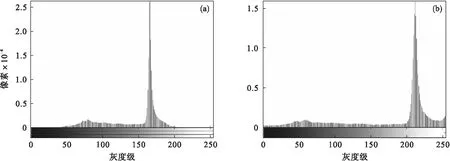
图4 图像灰度直方图调整前后对比

1.7 双能X射线图像融合

行李物品在经过双能安检设备后，会在高能探测器以及低能探测器上分别出现一幅包含有物品信息的扫描图像.有些内部结构较厚的地方可能在高能图像中显示较为清楚，而有些细微的结构则可能在低能图像中才能显示清楚，因此分别对高、低能安检图像进行上述处理以后，还需进行图像融合，将高、低能图像所包含的有用信息结合起来，生成一幅便于安检人员观察的图像.

常用的X射线融合方法有灰度最大值法、基于小波融合法[12]、加权平均法等，本文算法将采用主成分分析法对双能图像进行按权重融合，具体步骤如下：

1)分别将待融合的高、低能图像写成列向量的形式，并组成为一个n行、2列的矩阵，其中n代表待融合图像的总像素数.对上述矩阵求协方差矩阵，形式如下：

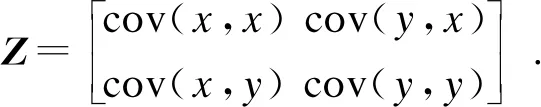
(13)

2)求取矩阵Z的特征值与特征向量.

3)设上述协方差矩阵中较大的特征值所对应的特征向量为(a0,a1)T，则第一幅图像的融合权重为a0/(a0+a1)，第二幅图像的融合权重为a1/(a0+a1) .

采用上述方法对图像进行融合，耗时较短，符合安检图像处理实时性的要求，且没有较明显的拼接痕迹.

2 实验结果对比与分析

为验证本文算法的可行性，搭建实验平台，采用Intel(R) Core(TM) i7-7700HQ CPU 2.80 GHz处理器，16 GB内存，Windows 10及64位操作系统，编译环境为MATLAB2018b.

实验设备采用沈阳地泰设备检测有限公司的DEX6550双视角X射线检查设备，该设备为16位数据采集系统，实验数据均来自沈阳地铁1，2号线的真实数据，原始图像的动态范围为[0,65 535].

针对本文算法所提出的一些可人为修改参数，取值如下：α=0.1，β=1，滤波次数l=3；滤波窗口w的半径依次选为2，12，22；b=0.8.

2.1 主观评价

对图像最直接、最可靠的评价方法便是主观评价.对安检图像来讲，主观评价一幅图像的好坏，主要是看安检人员能否看清包裹内的全部物品；当物品之间有重叠或内部结构较厚时，是否能将它们的轮廓全部分清.本文选取了在安检中较为常见的工具箱和手提包，处理前后的对比如图5所示.

图5 本文算法处理前后对比

由图5a、图5b可以很清晰地看到，在处理后，图像整体的对比度效果提升，细节得到增强，左上方电路板的纹路显示更加清晰，下方线圈的微小细节也得到显示；由图5c、图5d可以看出，整个箱内的重合物体在处理后，各自的边缘都能得到较为清晰的显示.

同时，将本文算法与对数压缩、基于Sigmoid函数压缩以及基于LEP滤波压缩进行对比，如图6所示，也可以清晰看出本文算法对图像的改善.

2.2 客观评价

为了避免受到光照等周围环境以及观察者本身状态、心理的影响，本文在对算法进行主观评价的同时，还将对调整后的图像进行客观评价[13]，采用的评价标准有信息熵、对比度提升指数以及峰值信噪比.

图6 不同算法对比

信息熵[14]描述的是一幅图像所含信息的丰富程度，其值越大，则表示图像中所包含的信息越丰富；对比度提升指数[15]是针对射线图像对比度普遍较低所提出的用来评价X射线在增强后对比度变化的指标；峰值信噪比[16]用来表示图像处理后的失真情况，其值越大，图像失真越少.

信息熵的计算公式为

(14)

式中：Pi表示灰度级为i的概率；G表示图像的总灰度级.

对比度提升指数的计算公式为

(15)

(16)

(17)

式中：Cori,Cpro分别表示处理前与处理后图像；m(·)为取均值；fmax(i,j)，fmin(i,j)表示输入图像的像素点(i,j)在3×3窗口内像素最大、最小值；gmax(i,j)，gmin(i,j)表示增强后像素的最大、最小值.

峰值信噪比的计算公式为

(18)

式中：M×Q表示原图尺寸(像素数)；f(i,j)，g(i,j)分别代表处理前后图像的灰度值.

本文利用上述3个客观评价标准对处理后图像进行评价，并对比本文算法与其他算法之间的差异，同时，为了规避实验数据较少给结果带来的偶然性，另外选取三幅图片进行实验，所得结果如表1所示.

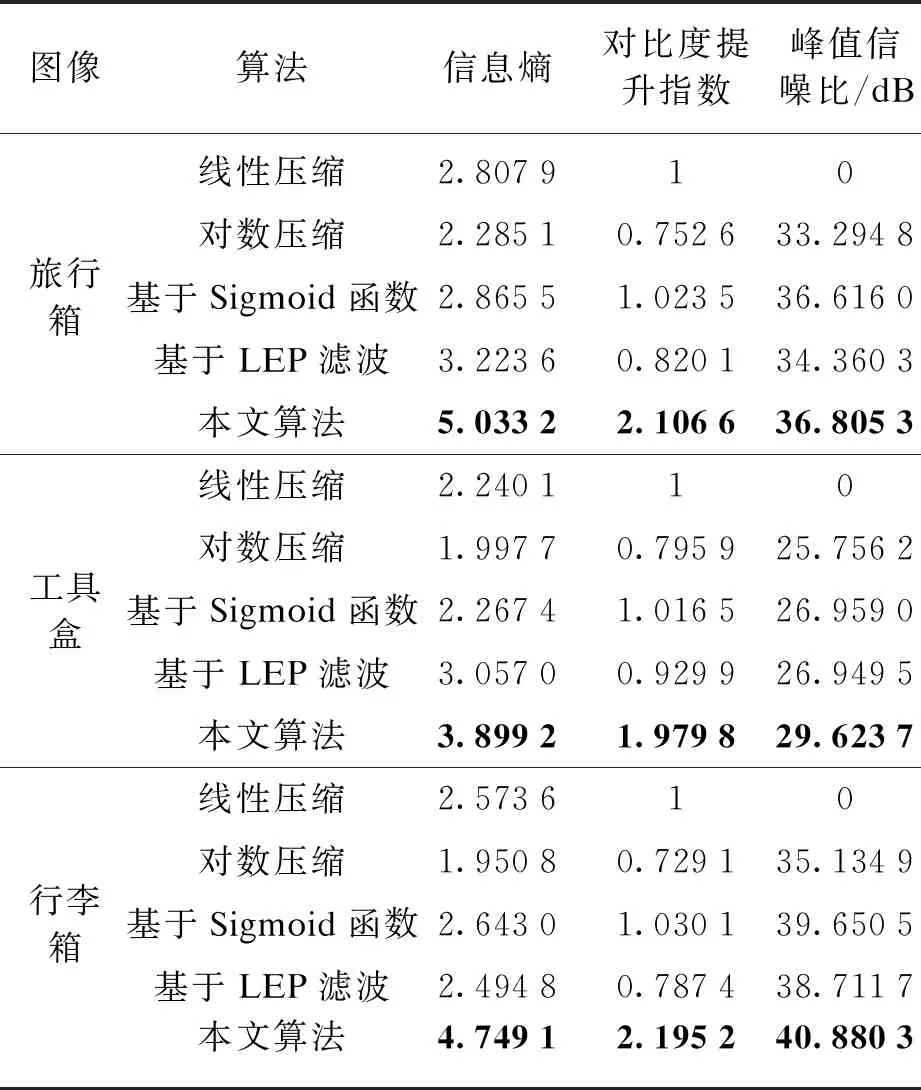
表1 不同算法客观评价

由表1可以看出，相较于其他色调映射算法，经本文所提算法进行动态范围调整后的图像，其信息熵、对比度提升指数、峰值信噪比都有显著提高，同时本文算法的平均处理时间在1.2 s左右，符合安检工作的实时性.这表明本文算法不仅能够有效压缩动态范围，同时能够增强图像所蕴含的细节信息、提高图像对比度及整体明暗程度，得到比其他算法更好的低动态范围双能X射线安检图像.

3 结 论

针对高动态范围双能X射线图像的特点，本文从实际出发，结合安检工作中对输出图像的实际需求，应用局部保边滤波器对输入图像进行迭代滤波，并对得到的细节层以及基础层同时进行自适应处理，之后将它们相加.最后进行直方图均衡化操作并按照权重融合高、低能图像，得到低动态范围双能X射线安检图像.实验结果表明，本文算法在压缩动态范围的同时，能够改善安检图像的缺点，得到细节清晰、对比度高、更加便于安检人员观察的图像，符合实际要求.后续可将本算法针对实时线扫描系统，并结合双视角进行改进，得到实时无痕的清晰图像.