基于改进理想点模型的岩体结构面分级方法

2021-01-15王述红朱宝强

东北大学学报（自然科学版） 2021年1期

王述红，朱宝强，张泽

(东北大学资源与土木工程学院，辽宁沈阳 110819)

岩体由各种各样杂乱无章的结构面和块体组成，结构面按成因可分为原生结构面、次生结构面和构造结构面.大量的工程实践表明，岩体的破坏常常是沿着控稳结构面的破坏，在工程扰动情况下，结构面的力学效应及岩坡和隧道的稳定性主要取决于结构面规模和工程地质特性[1-2]，因此对结构面进行“分级”对于进一步深入研究结构面特性[3]及分析岩体稳定性有重要意义.

目前，对于岩体分级[4-6]和围岩分级[7-9]的研究较多，而针对结构面的分级方法，主要为宏观分析，如谷德振[10]在1979年依据结构面的规模将其分为5级，然而该分级体系的宏观性导致了其更适合于大范围的区域地质稳定性研究，不便于指导工程实践.张倬元等[11]又根据结构面对岩体力学行为的影响程度，将其划分为贯通性宏观结构面、显现结构面和隐微结构面，该分级同样较为宏观.后来，向波等[12]在总结了前人研究的基础上，加入了部分定量指标，并结合相关国家标准将结构面分为更加细致的5种级别.Sun等[13]结合四川省峨眉山某水电站工程，将现场结构面细分为4组9个亚类，为类似地区结构面的分级提供了参考.

上述研究均不同程度地推进了结构面分级体系的发展，但研究多为宏观上的定性判断，不便于指导工程设计和施工.鉴于此，本文将多指标评价的理想点模型引入结构面分级中，通过对模型权重求解进行改进，提出了一种基于改进理想点模型的结构面定量分级方法，并将该方法应用于重庆市兴隆隧道现场实测的典型结构面分级中，将分级结果与实际工程进行对比分析，验证了所提方法的可靠性和实用性.

1 结构面分级的多指标评价体系

影响结构面分级的因素有许多，本文对结构面的定量分级主要是结合向波等[12]提出的定性及半定量分级体系(见表1)，该分级体系中结构面分级的主要影响因素有：①结构面两侧岩壁岩性、强度及风化程度；②结构面的粗糙度；③结构面充填物性质；④结构面富水程度.

表1 结构面分级体系

根据以上所述各影响因素，为便于计算，指标应选取定量或半定量指标，对于定性指标，则应进行定量化处理，类比“岩体分级”[4-6]及“围岩分级”[7-9]中指标选取方法和指标获取可行性，确定以下7个指标对结构面分级进行定量表征，主要包括：泉流量(X1)、岩石基本质量指标(X2)、单轴饱和抗压强度(X3)、岩体完整性系数(X4)、风化系数(X5)、充填系数(X6)、粗糙系数(X7)，并以此为依据将结构面分为5级，多指标分级体系如图1所示.

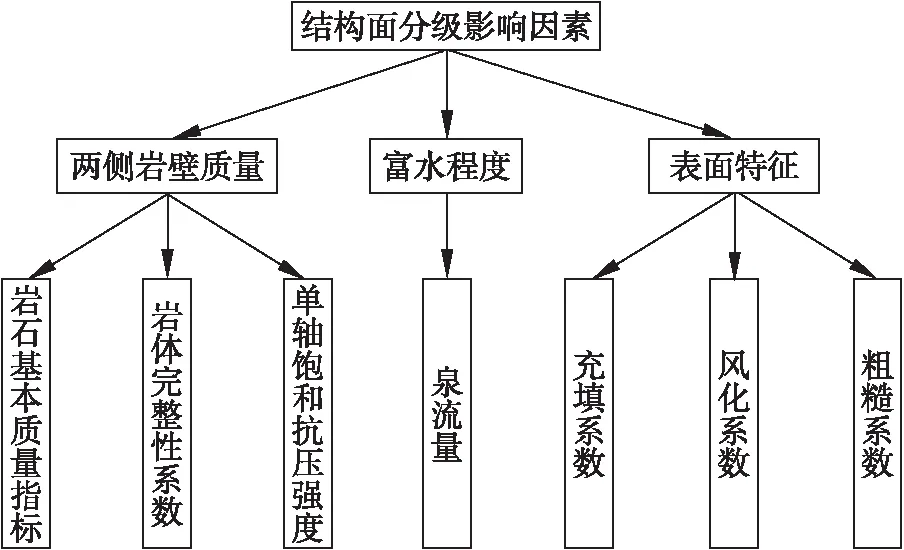
图1 结构面多指标分级体系

2 结构面分级的改进理想点模型

理想点模型是由Hwang和Yoon[14]于1981年提出的基于多指标的多方案分析方法.该方法操作简单，不需要复杂的计算过程，结果十分客观[15].本文将其引入结构面的分级中，充分利用原始结构面数据信息，对结构面进行定量分级，并针对该方法权重确定较为主观的缺点，提出了对该方法进行改进，利用层次分析法求得主观权重；然后结合熵权法确定客观权重，并利用最小熵原理优化主、客观权重，由此确定分级指标的最优组合权重.建立结构面分级的改进理想点模型，从而对结构面进行合理分级，为后续抗剪强度确定及岩体稳定性分析奠定基础.其主要流程如图2所示，为便于工程应用，笔者基于Matlab平台编制了该部分程序.

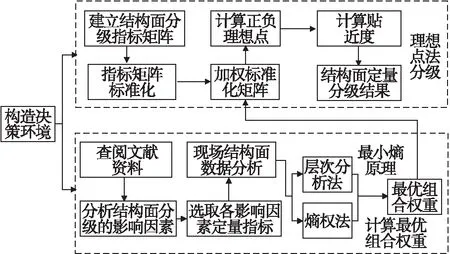
图2 改进理想点模型分级流程

2.1 结构面分级指标量化

对于泉流量(X1)，结合实际工程确定其定量评价指标见表2.对于岩石基本质量指标(X2)、单轴饱和抗压强度(X3)、岩体完整性系数(X4)，其指标量化采用国标分级标准，见表3.对于风化系数(X5)、充填系数(X6)、粗糙系数(X7)，结合GSI岩体质量分级法中的SCR部分确定其定量化评价指标，见表4.

综上，可得到结构面分级各指标的定量化汇总结果，见表5.

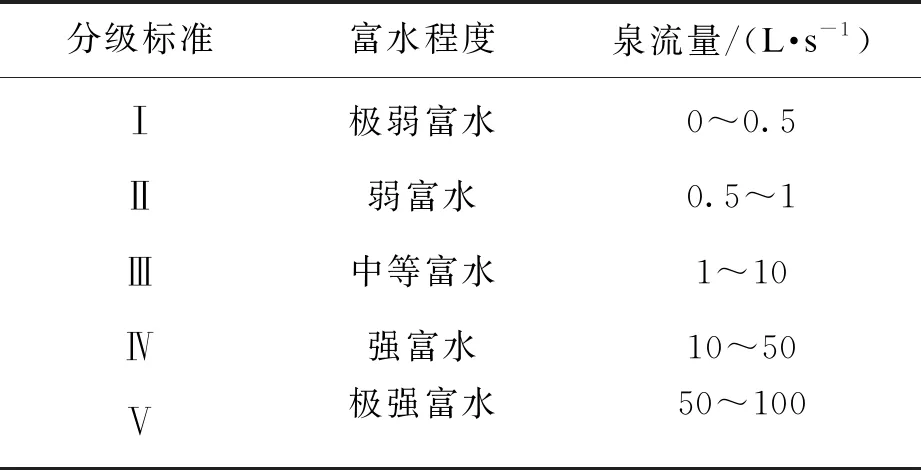
表2 结构面富水程度评价指标量化

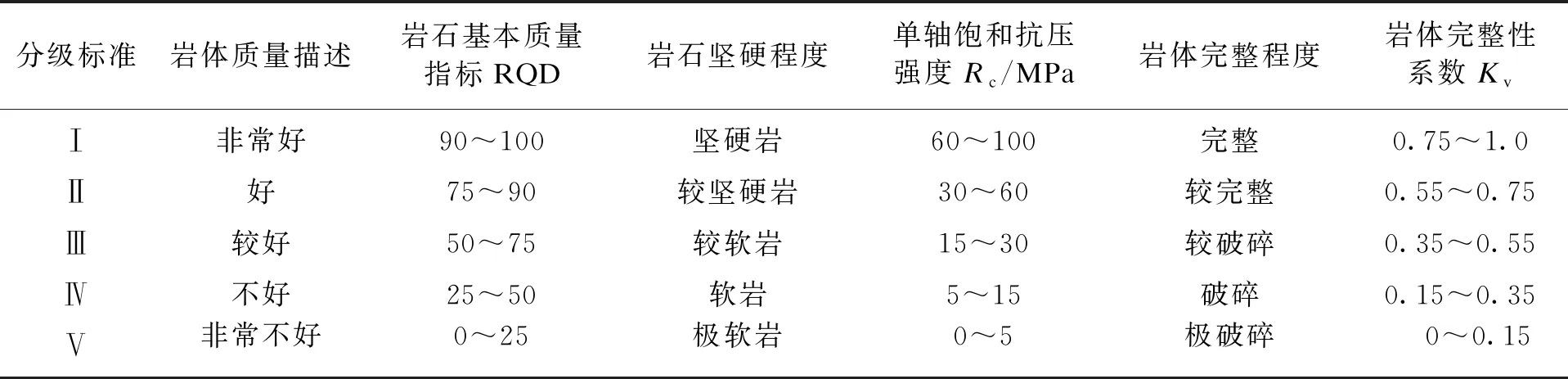
表3 结构面两侧岩壁质量评价指标量化

表4 结构面表面特征评价指标量化

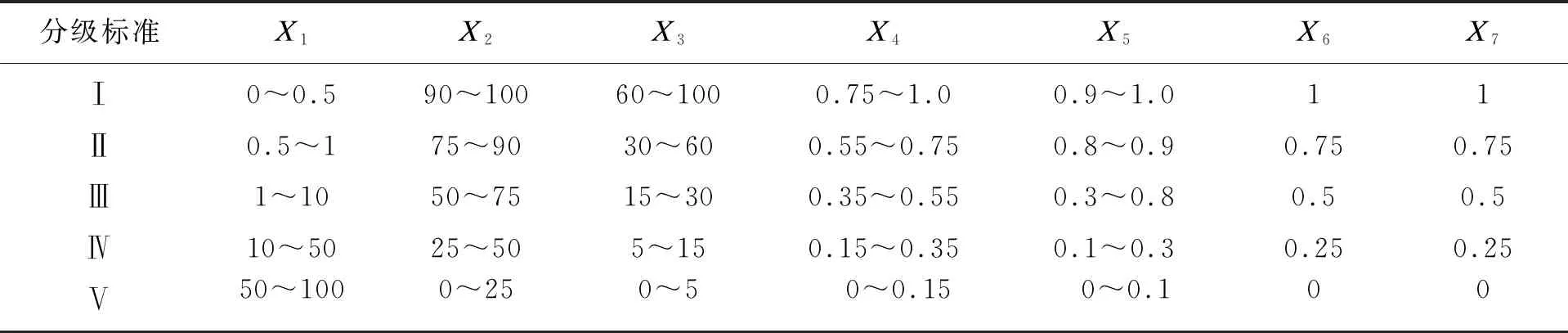
表5 结构面定量分级指标

2.2 建立分级指标矩阵

设有m个待分级结构面样本，含有n个分级指标，对应的评估值xij(i=1,2,…,m;j=1,2,…,n)，则分级指标矩阵为

(1)

2.3 分级指标矩阵标准化

由于结构面各分级指标具有不同量纲及量纲单位，为了消除该影响，需要对指标进行无量纲化，经过标准化后的分级指标矩阵为

(2)

对于收益型指标：

对于消耗型指标：

2.4 加权标准化分级指标矩阵

2.4.1 层次分析法确定主观权重

2.4.2 熵权法确定客观权重

熵权法是一种客观赋权法，它仅依赖于数据本身的离散性，目前已经广泛应用于工程技术领域，采用该方法确定分级指标客观权重的具体步骤如下：

1)建立原始结构面数据评价矩阵：

P=(pij)m×n.

(3)

式中，pij为指标初始评价值.

2)归一化原始矩阵，得到标准矩阵：

P*=(pij*)m×n，

(4)

(5)

3)设ωj′为第j个评价指标的熵权，即所求客观权重，则

(6)

2.4.3 确定最优组合权重

为弥补单一赋权带来的缺陷，本文利用层次分析法求得各分级指标的主观权重ω*，利用熵权法确定客观权重ω′，ω′=(ω1′，ω2′，…，ωn′)，以此来修正主观权重，最终得到最优组合权重ω，为使三者尽可能接近，依据最小熵原理对主、客观权重进行组合，即

(7)

然后利用拉格朗日乘子法得到最优组合权重为

(8)

2.4.4 加权标准化分级指标矩阵

将最优组合权重与标准化分级指标矩阵相乘，得到加权标准化矩阵F=(fij)m×n=(ωjyij)m×n，即

(9)

2.5 构建评价指标体系

2.5.1 理想点和反理想点的确定

评价指标一般分为收益型和消耗型[17-18]，收益型指标越大越好，消耗型指标越小越好，此时结构面所属等级也就越低.本文中泉流量属于消耗型指标，其余指标均为收益型.若指标单调变化，则可定义如下理想点和反理想点.

当指标为收益型时，定义

(10)

当指标为消耗型时，定义

(11)

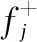
2.5.2 构建理想点评价函数

各分级方案与理想点的距离采用欧氏距离来度量，具体含义为距离理想点越近，反理想点越远，分级结果就越好，具体公式为

(12)

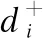
2.6 贴近度分析

对于一组结构面数据，当分级指标距理想点越近，距反理想点越远时，表明该结构面等级越靠近理想点(即，等级越高)，该程度可以用贴近度β来表示，即

(13)

基于上述原理，可根据贴近度判断各结构面所属等级，判断规则见表6.

3 工程实例

重庆市三环高速公路合川至长寿段兴隆隧道位于重庆市渝北区木耳镇良桥村，隧道在构造上位于重庆-沙坪向斜北西翼与龙王洞背斜之间，隧址区围岩岩性主要为侏罗系上沙溪庙组中风化砂岩和泥岩，岩体结构呈大块状，富水程度较低.

本文以现场实测的15条具有代表性的结构面数据为例，进一步验证改进理想点模型应用于结构面分级中的可靠性和实用性，结合现场各工点原位试验结果，采用文献[12]所述方法确定各结构面所属等级.

3.1 确定无量纲化分级指标矩阵

对实测的15条结构面的各分级指标按式(2)进行无量纲化，得到无量纲化的分级指标见表7.

3.2 确定分级指标的组合权重

利用层次分析法，结合结构面特征参数及专家意见，确定各分级指标的主观权重为

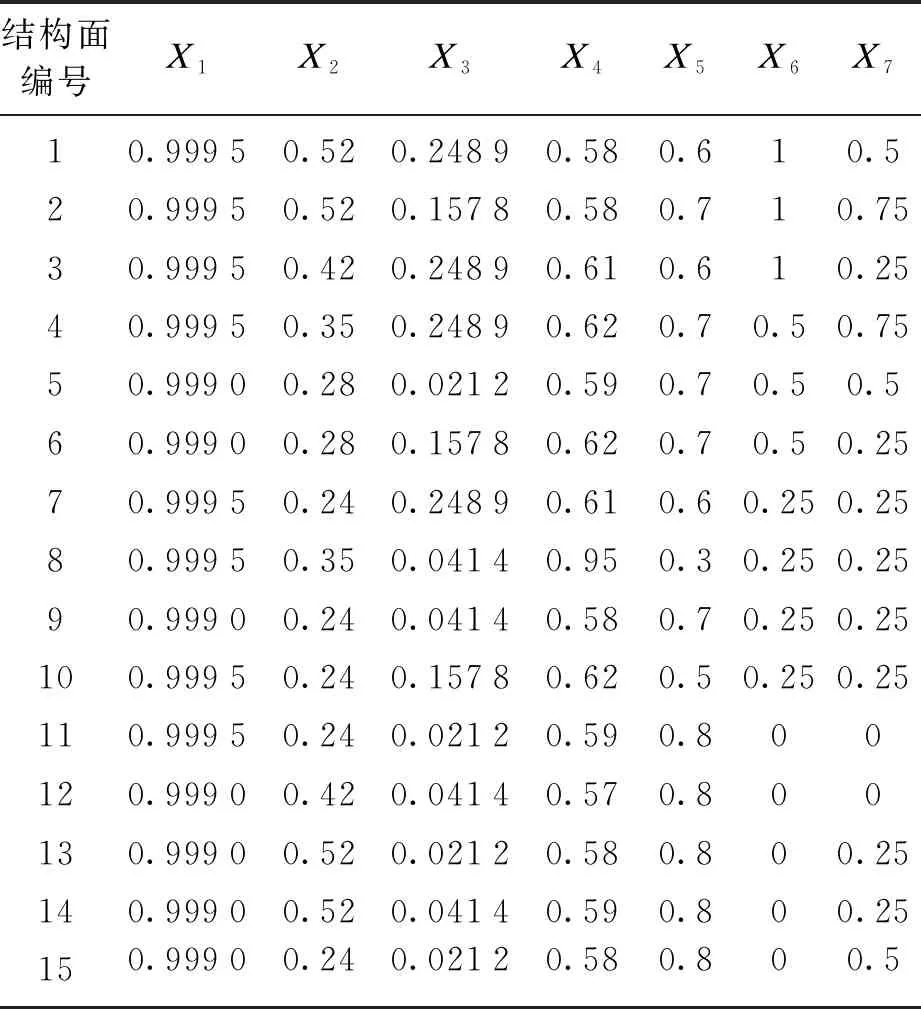
表7 实测结构面分级指标(无量纲化)

ω*=(0.108 7,0.110 7,0.142 5,
0.085 7,0.079 5,0.308 2,0.164 7).

然后利用式(3)～式(6)中熵权法计算得到各分级指标客观权重为

ω′=(0.031 7,0.085 0,0.280 8,
0.053 4,0.069 3,0.302 1,0.177 7).

然后由式(7)，式(8)确定最优组合权重为

ω=(0.074 4,0.069 4,0.210 7,
0.026 5,0.049 5,0.389 6,0.189 9).

3.3 加权标准化分级指标矩阵

确定最优组合权重后，将表5中分级指标无量纲化，并结合表7中无量纲化后的15条实测结构面，代入式(9)可求得加权标准化分级指标矩阵为

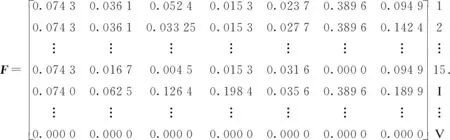
3.4 确定理想点和反理想点

将加权后的标准化矩阵代入式(10)，式(11),可求得理想点与反理想点为

3.5 确定贴近度

将3.3节及3.4节计算结果代入式(12)，式(13)，确定实测结构面及各等级结构面贴近度分别见表8和表9.

3.6 结果分析

结合表6中分级标准及表8和表9中贴近度计算结果，确定各条结构面所属分级结果见表10，各方法与实际分级数量的误差对比结果如图3所示.

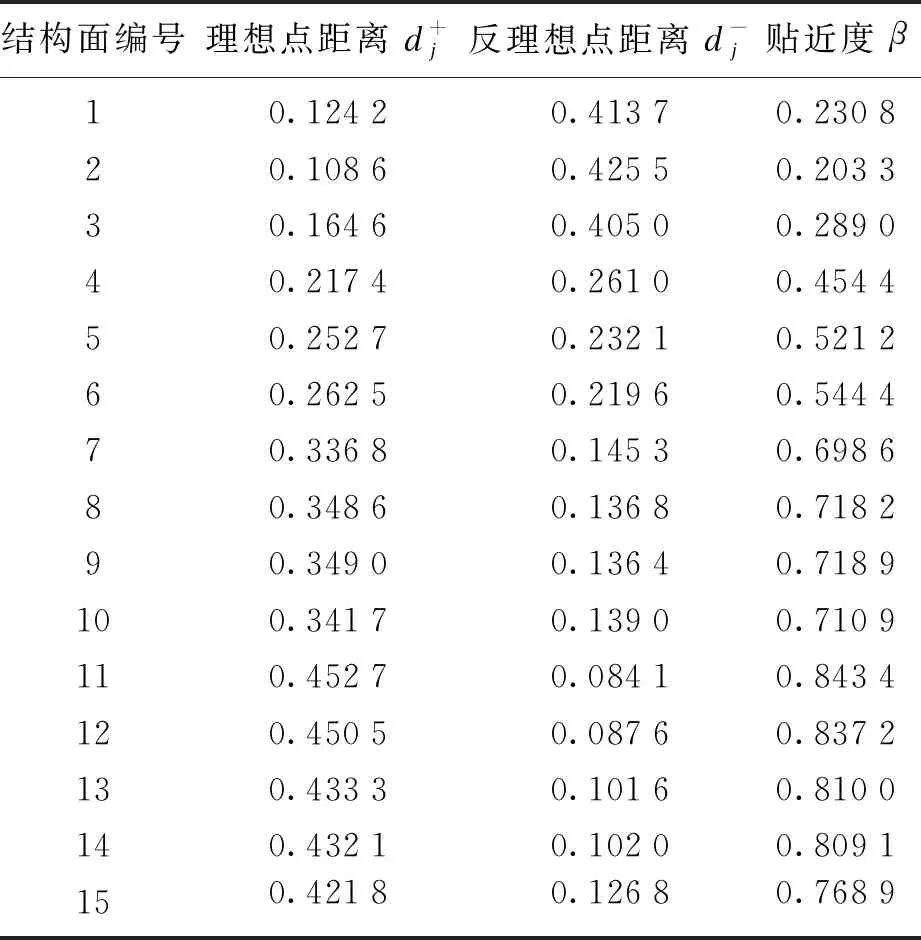
表8 实测结构面贴近度计算结果

表9 各等级结构面贴近度计算结果

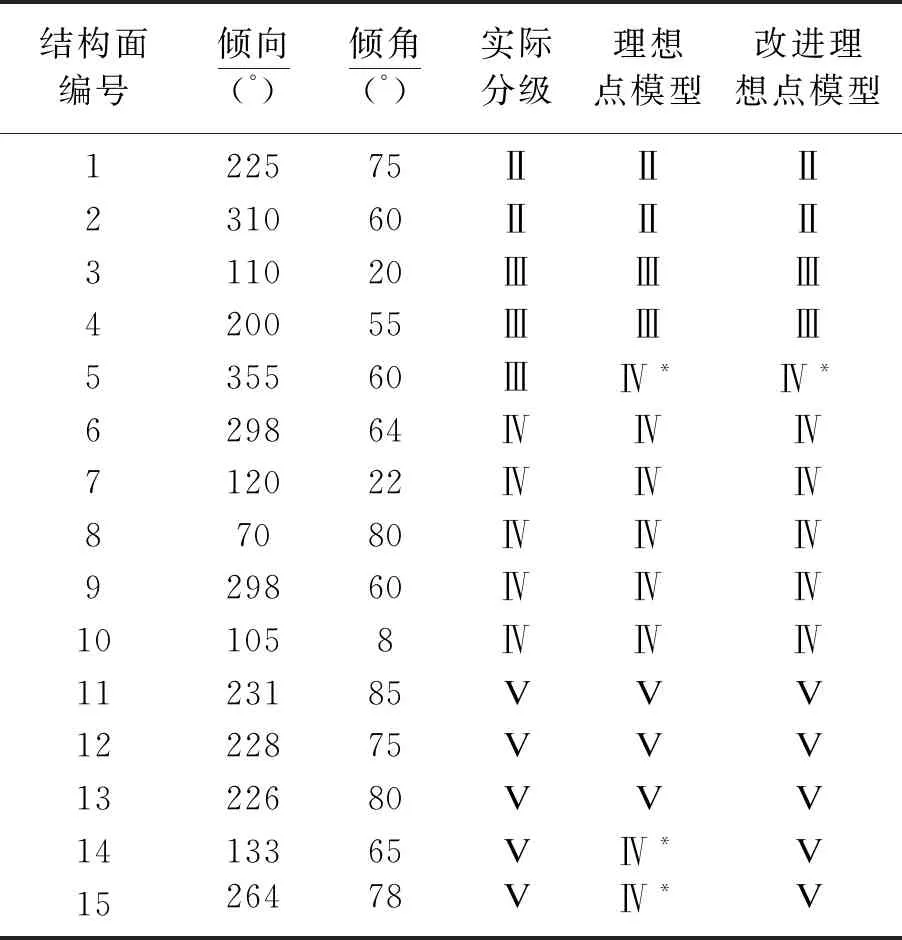
表10 结构面定量分级结果

图3 结构面分级结果误差对比

由表10及图3中的对比结果可知，本文所提改进理想点模型在应用于结构面分级时，仅第5条结构面等级划分结果(Ⅳ级)略高于实际分级(Ⅲ级)，整体分级结果与实际较为接近.进一步分析出现分级偏差的结构面可知，该结构面贴近度计算结果为0.521 2，与分级标准中的0.508 3较为接近，分级时将介于两级之间的结构面判别为其中一级，事实上，由于结构面等级越高，其性质也越差，因此按高等级结构面分析实际工程时更有利于保证施工安全，即判别结果偏于保守，也说明了本文方法具有一定的可行性.另外，改进理想点模型分级的准确率为93.3%(1条分级出现偏差，14条分级准确)，远优于改进前理想点模型(准确率80%，3条分级出现偏差，12条分级准确)，表明了本文方法应用于结构面分级中具有较好的工程实用性.