微粒受介电泳效应的动力学建模和仿真
2021-01-15胡晟,王克,蔡露
胡 晟, 王 克, 蔡 露
(东北大学秦皇岛分校 控制工程学院, 河北 秦皇岛 066004)
介电泳(dielectrophoresis, DEP)作为一种微/纳粒子操控、分离、富集和输运技术,已经受到国内、外学者的广泛关注和学习[1-4].在非均匀电场作用下,粒子电极化的应力不平衡,因此会发生沿电场强度梯度方向的定向运动.微粒向电场强度较强区域运动,该介电泳力称为正介电泳力(positive DEP, pDEP).反之,负介电泳力(negative DEP, nDEP)则驱使粒子运动到电场强度较弱的空间位置.上述正、负介电泳力的选取主要与粒子或溶液的介电常数、电导率和激励频率有关.伴随数学物理方法和计算方法学的飞速发展,目前介电泳的理论研究也取得了长足的进步.根据经典电偶极矩法[5-6]和Maxwell应力张量法[7-8]关于介电泳力的物理描述,粒子运动轨迹和拓扑形态的仿真结果,都有效地证实了实验观测和电极设计.
然而,从当前的数学建模和仿真分析来看,粒子承受介电泳力作用的动力学研究仍然存在一些问题需要进一步研究和解决,主要由于编程的复杂以及后期代码的维护工作.特别对于粒子承受排斥力与介电泳吸附效应等问题时,粒子相互作用力的受力矩阵也导致了求解精度和迭代次数的成倍增加,而关于代码的优化和电场偏微分方程的求解仍需要一个更好的方法和工具进行优化求解.基于COMSOL Multiphysics 5.3a有限元分析软件通过各种内置的方法已经极大解决了物理域的网格离散和偏微分方程求解.通过Laplace微分方程和边界条件的设定,可以快速得到电极芯片内部的电压分布[9-10],从而掌握电场变化的方向和强度.COMSOL Multiphysics 5.3a软件提供了粒子跟踪模块(particle tracing module, PTM),该模块极大扩大了场与粒子相互作用的研究内涵.可以根据求解得到的物理场进行粒子运动特征的分析和学习.Zhao等[11]最早采用PTM和AC/DC Module结合的方法进行了粒子受介电泳效应的动力学研究.但是他们研究所提供的相关信息相对较少,并且介电泳粒子成链效应仍存在研究不足等缺点.本文重新对粒子位于介电泳芯片的粒子受力运动问题进行了仿真和研究,丰富了COMSOL Multiphysics 5.3a软件在介电泳粒子操控领域的理论研究,使该软件提供的AC/DC和PTM模块可以较好解决现有Velocity-Verlet或ODE算法编程困难、执行效率低的问题.
1 原理与物理场模型
微粒的介电泳力产生机理归因于电场分布的非均匀特性,从空间角度观察粒子运动可分为全局和局部效应.全局介电泳效应主要是电极产生的电场在较大尺度空间诱导粒子输运和富集.但是局部介电泳效应,则是微粒迫使均匀电场在局部或粒子附近发生扭曲,进一步诱导周围粒子移动成链的过程.在无损耗介质溶液中,电极产生的介电泳力表达式[1]为
FDEP=(p·)E.
(1)
式中:E为外界激励电场强度;为哈密顿算子;p为粒子的电偶极矩,其表达式[5,12]为
p=4πε0εma3βE.
(2)
式中:ε0和εm分别为真空介电常数和溶液的相对介电常数;a为粒子的半径;β=(εp-εm)/(εp+2εm),代表粒子与溶液的电极化率,εp是粒子的相对介电常数.
然而,粒子承受的局部介电泳力与它们之间的电偶极矩动量密切相关,表达式[5,13]为
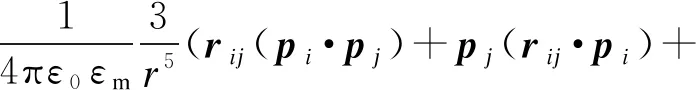

(3)
式中:pi和pj分别为i粒子和j粒子各自的电偶极矩,可由式(2)计算得出;rij是i粒子和j粒子的单位方向矢量;dij是标量,代表了i粒子和j粒子之间的欧拉距离.需要注意,COMSOL Multiphysics 5.3a的PTM中,关于Particle-Particle Interaction应力项提供了dest子函数用于求解剩余粒子的空间位置.通过Variables对话框编写上述函数解析式作为内联函数,以便于应力求解所需.
另外粒子相互碰撞和迁移还应包含相互排斥力,防止粒子发生重合现象,表达式[13-14]为
(4)
式中:δmin为两个粒子之间的最短距离;1/κ为排斥力作用范围;Frep0为标量值,通常等于静电力大小.
粒子在运动过程中还受Stokes拖曳力,并且粒子所受的重力分别满足式(5)和式(6).
Fs=6πηau,
(5)
(6)
式中:u为粒子移动速度;η为溶液黏度;ρp和ρm分别为粒子和溶液的密度;g则是重力加速度.对于i和j粒子的应力模型,如图1所示.此外,粒子下方的芯片底面也需要设置排斥力,防止粒子运动至求解域外.
(7)
式中:Fw0是墙壁给予粒子的最大排斥力;ri是i粒子的空间位置(xi,yi,zi).式(4)和式(7)的初始值Frep0,Fw0和1/κ分别取值2.3×10-12N,1×10-10N和0.01.同时,求解域中剩余5个墙壁面,设定Freeze边界条件,有利于粒子的观测和学习.

图1 微粒受力示意图
2 结果和讨论
2.1 均匀电场
首先进行平行极板产生均匀电场的求解,图1中,左、右边界分别设定+3.5 V和接地边界条件,其余边界为绝缘边界条件.通过求解Laplace方程,即式(8)和式(9),可得到施加电压后芯片内部的电场分布[15].
E=-V,
(8)
D=ε0εrE.
(9)
式中:V为电势的标量场;εr为溶液与粒子的相对介电常数.相关的仿真参数如表1所示.根据上述应力表达式的简要说明,采用PTM获取AC/DC的电场数值进行粒子应力模拟.因此得到相关的粒子运动结果,如图2所示.在均匀电场中,粒子受局部介电泳效应将发生定向迁移,最终形成一定长度的珍珠链结构.同时,PTM模块的灵活可编程特点,也能进行不同尺寸粒子在均匀电场应力下的运动特征分析.图3为粒子半径为 5 μm 和2.5 μm时的仿真结果.从图中发现,混合了不同尺寸粒子很难实现珍珠链结构,主要归因于偶极子之间空间对称性不匹配.

表1 仿真模型关键参数
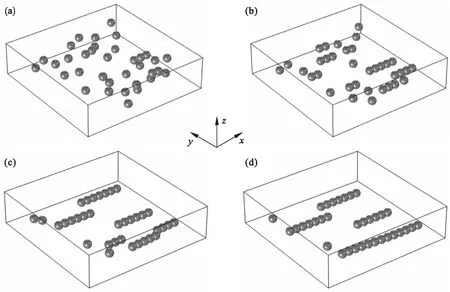
图2 均匀电场下,35个粒子且半径为5 μm的仿真结果
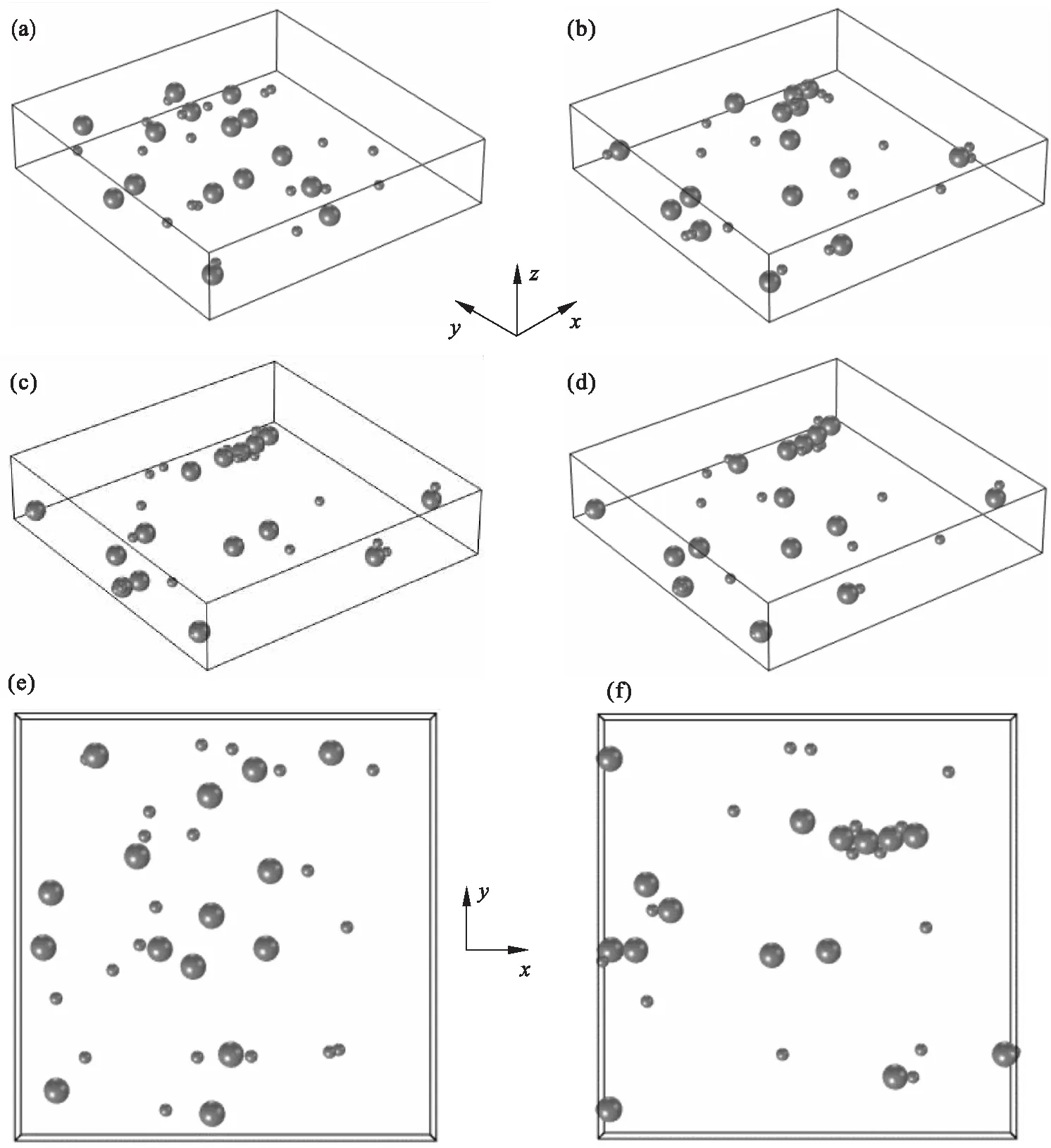
图3 均匀电场下,15个半径为5 μm和20个半径为2.5 μm的粒子仿真结果
2.2 非均匀电场
设置金属电极产生非均匀电场,诱导粒子向电场较强或较弱方向运动.激励电极如图4a所示,右侧负电极接地.电极电压仍为+3.5 V.聚苯乙烯粒子εp为2.25,受负介电泳力运动到电场强度较弱位置,并且局部形成短链结构,如图4c所示.然后对粒子表面进行化学修饰,假设微粒εp为120,高于水溶液80,电极针尖附近的粒子将运动到其附近,如图4d所示.但是远离针尖的粒子所受正介电泳力相对较弱,则逐渐沉淀至芯片底部.
另外采用电极阵列型结构计算区域内35个半径5 μm的微粒运动结果,如图5所示.负介电泳效应时,靠近边缘的粒子运动到电极与电极之间电场较弱区域.反之正介电泳力驱使粒子到电极边缘位置,该模拟结果也与文献[16-18]实验基本类似.
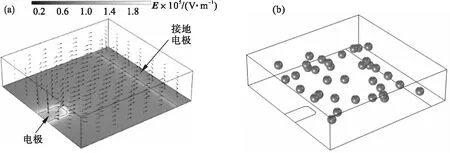

图4 非均匀电场下,半径为5 μm的35个粒子承受负、正介电泳力仿真结果

图5 阵列型电极结构中,粒子承受负、正介电泳力的仿真结果
3 结 论
1) 本文采用了COMSOL Multiphysics 5.3a软件,通过求解Laplace方程获得求解域内的电场分布;后期耦合了粒子追踪模块,模拟芯片内微粒受介电泳效应的运动行为.
2) 仿真结果表明,本文方法能有效降低计算程序的繁琐程度,提高动态模拟的人机可视化效果.较好解决现有Velocity-Verlet或ODE算法编程困难、执行效率低的问题.
