基于降噪回溯SAMP算法的Massive MIMO信道估计
2021-01-15李春树
徐 昊 李春树,2
1(宁夏大学物理与电子电气工程学院 宁夏 银川 750021) 2(宁夏沙漠信息智能感知重点实验室 宁夏 银川 750021)
0 引 言
在传统MIMO系统中,天线数量较少,基站最多配置8根天线。为了满足人们对高速数据传输的要求,引入了Massive MIMO的概念。在Massive MIMO系统中,基站处配置了上百根天线,在同一时频信道上为几十个用户提供服务,提供了很大的空间自由度。根据信息论,基站天线数目越多,系统的频谱效率也成比例增加。因此,Massive MIMO的优势主要在于频谱效率高,能量效率高,抗干扰能力强。在使用Massive MIMO移动通信的过程中发送信号会受到无线信道和噪声的影响而发生畸变,这就使得接收端无法正确接收发送信号。为了能无失真地恢复发送端的信息,接收端须利用信道估计技术来准确地估计信道状态信息并对接收信号进行相应的补偿。故信道估计的好坏影响了通信系统的性能,成为无线通信系统中的一个关键技术。对于Massive MIMO系统,庞大的天线数量和用户数量,使得信道估计在复杂度和导频需求方面成倍增加,信道状态信息获取十分困难。为改善Massive MIMO的系统性能,促进无线通信技术的发展,Massive MIMO信道估计的算法成为当前研究的热点问题[1-5]。现有的信道估计方法主要有LS算法和MMES算法[6]。但是由于Massive MIMO系统中信号矩阵维数较大,导致传统算法的计算量十分庞大,并不适用于实际。针对信号的稀疏性,压缩感知算法应运而生[7]。该算法大大降低了计算复杂度,在图像、信号处理等领域得到广泛应用。传统的压缩感知算法有OMP算法[8]、CoSAMP算法[9-10]、SAMP算法[11]等。通过对该类算法的研究,本文针对SAMP算法中元素选择和未能有效去除噪声的问题,提出降噪回溯SAMP(NrSAMP)算法。
1 Massive MIMO信道模型
考虑文献[12]中Massive MIMO系统上行链路模型如图1所示,每个蜂窝小区中有K个单天线用户,共有L个小区。每个小区配置一个基站,该基站配置了M根天线并采用中心激励的方式来服务于K个用户。蜂窝小区中一个单天线用户发送的训练序列为X,Y表示上行链路的接收信号。
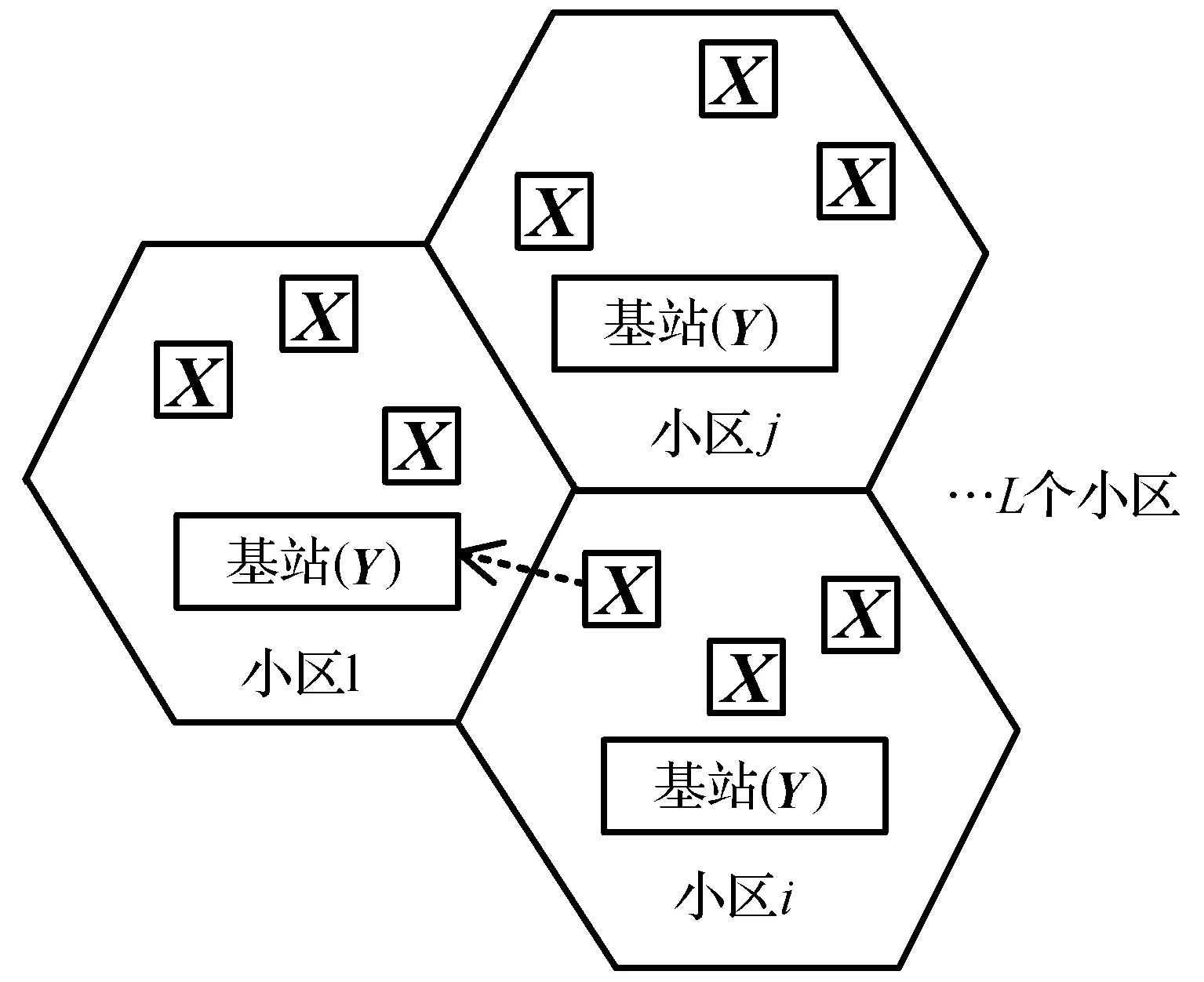
图1 Massive MIMO系统模型
令H1l∈RM×K为第l个小区内用户到第一个小区基站信道矩阵参数,由于Massive MIMO系统特性,信道矩阵中用大尺度衰落和小尺度衰落表征其衰落特性:
Hli=GliDli
(1)
式中:Gli表示第i个小区内K个用户到第l个小区基站的M根天线之间传播的小尺度衰落,是一个M×K维的均值为0、方差为1的高斯随机矩阵。Dli表示第i个小区内K个用户到第l个小区基站之间传播的无线传播衰落系数,来模拟信道中的大尺度衰落,是一个K×K维的对角矩阵。令小区用户发送训练序列长度为J。因此,目标小区l基站接收到的信号表示为:

(2)
式中:Hl是L个小区内的所有用户对目标小区的合成信道矩阵,其维度为M×KL;X表示L个小区内所有用户发送的训练序列的合成矩阵,其维度为KL×J;Nl为一个M×J的高斯噪声矩阵。将式(2)进行转置操作,可得到:
(3)
2 压缩感知与重构


(4)
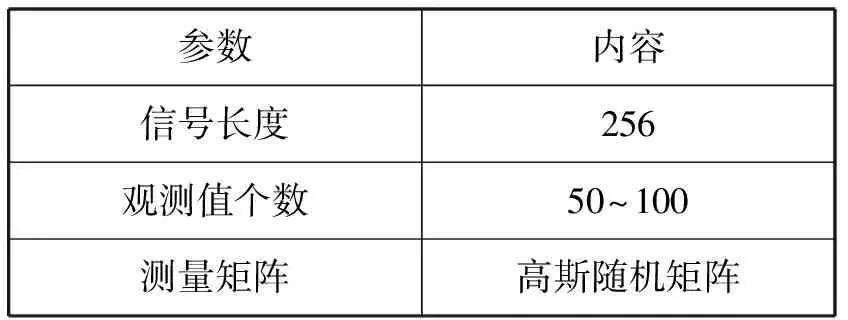
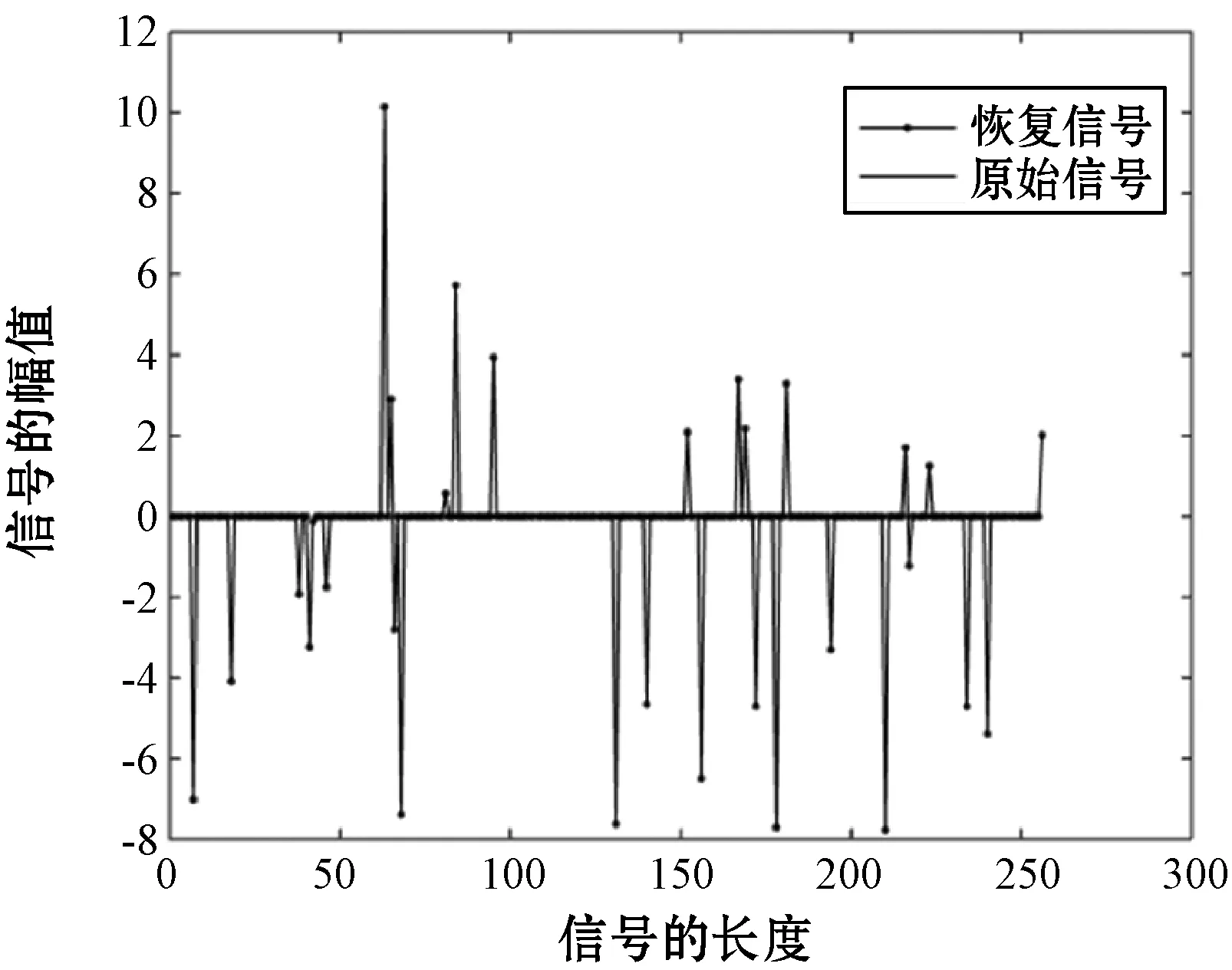
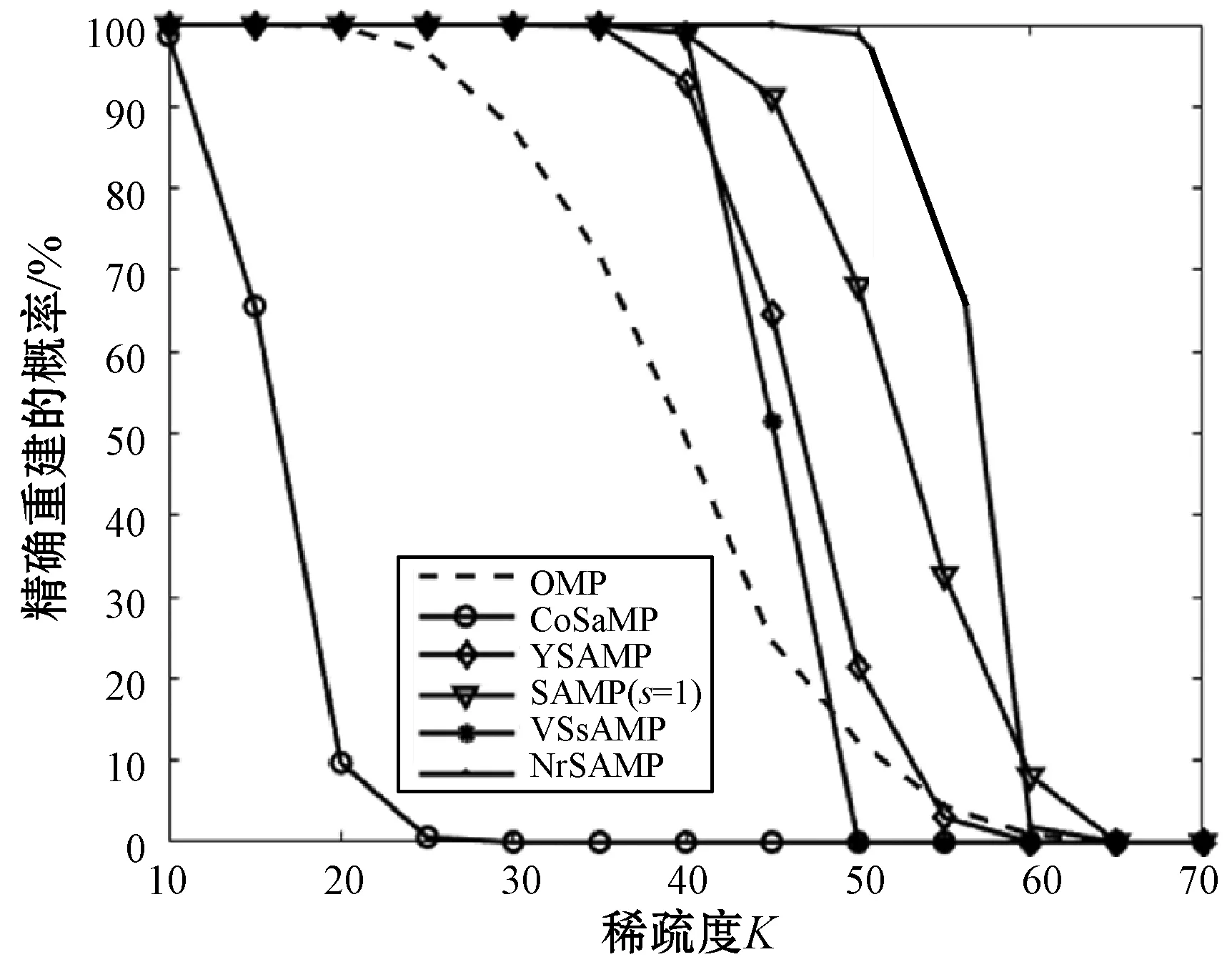
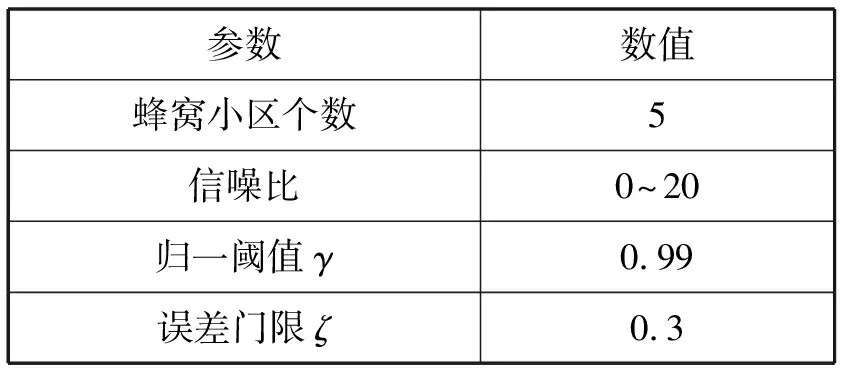
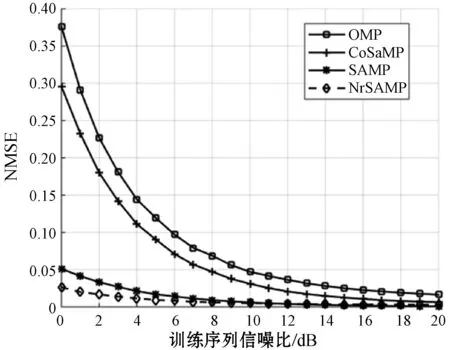
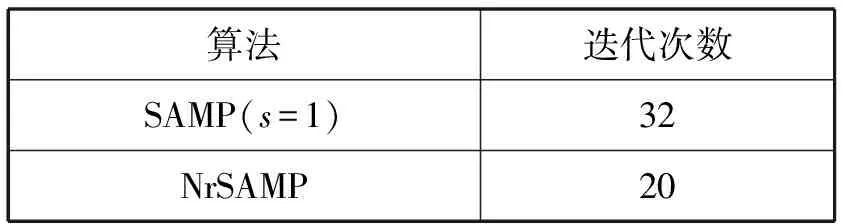
式中:Θ是投影系数,且Θ为[θi]=[ Z=ΦK=ΦΨΘ (5) 将式(5)与式(3)比较,通过Z和Φ可重构出信号K,将压缩感知算法应用于信道估计时,令Z为基站接收信号Y,Φ为小区发送信号X,重构信号K为估计的信道模型H。如此对应,可以得到式(6),证明可以通过压缩感知算法来实现对信道的估计。 Y=XH (6) 式中:Y为M×1的列向量,是M个观测值;X为M×N的测量矩阵。常见的测量矩阵有高斯矩阵、伯努利随机矩阵等。在接收端由式(6)通过重构算法求出信号X的N个元素。压缩感知信道估计主要分为:导频序列的构建;导频采样点的观测值Y;根据采样值和测量矩阵来恢复完整信道。 自然环境中噪声对信号有很大的影响,这会导致信号畸变严重,然而在一般的压缩感知算法中并没有对噪声进行相应的处理。本文提出利用奇异熵[13-14]理论对信号进行降噪处理,通过设置合适的阈值筛选出包含信息量较大的原子,改进算法中原子选择的方法。 假设XM×N为一个受噪声污染的信号。根据奇异值分解理论,对一个信号矩阵,有一个M×l的矩阵U,一个l×l的对角矩阵Λ和一个n×l的矩阵V使得式(7)成立。 (7) (8) (9) (10) 传统的贪婪类算法需要事先知道信号的稀疏度,然而这在现实生活中是难以确定的。所以SAMP算法是为了弥补稀疏度未知这一条件而产生的稀疏度自适应匹配追踪算法。现有研究中包括对SAMP算法的一些改进算法,例如:通过比较循环前后残差大小判断加大或是减小步长用以逼近信号稀疏度的改进的SAMP(YSAMP)[15]算法;通过设置阈值调整步长变化,使得大步长逐渐减小逼近稀疏度,从而减少运算时长的变步长稀疏度自适应匹配追踪(VsSAMP)[16]算法等。这些算法是针对SAMP算法中步长固定不变,可能存在过估计以及迭代次数的问题而提出的算法。利用表1中的参数来对SAMP算法以及其相应的改进算法进行测试,结果如图2和图3所示。 表1 SAMP算法参数选择 图2 不同步长测量次数与重构精度的关系 图3 在低测量次数下SAMP算法与其改进算法的重构精度比较 对图2和图3分析可知,测量次数较少的情况下,YSAMP算法对信号的重构精度要低于VsSAMP算法,当SAMP算法的步长为1时,信号的重构精度最佳。虽然步长为1使得每次迭代选取的原子数少,造成迭代次数增加,但所获得的精度最高。测量次数越多,文献[15-16]中提出的改进算法能够逼近步长为1时的测量精度。但是考虑到信号在发射过程中会有大尺度、小尺度衰落、噪声等对信号的影响,因此对信号进行降噪处理是必要的。 为了能在NrSAMP算法的初始阶段使用一个恰当的步长而不是通过残差或阈值的判断后回溯算法重新计算再进行比较计算得到合适的步长,本文利用有限等距特性(RIP)[17]对信号的稀疏度进行预估计,并利用此稀疏度作为步长可有效减少算法的迭代步数并获得良好的重构精度。测量矩阵Φ的RIP参数δ2k为式(11)中的最小δ。 (11) 因此,本文提出的基于降噪回溯SAMP(NrSAMP)算法的伪代码如下: 输入:接收信号y为测量向量,发送信号矩阵X对应为测量矩阵Φ,门限值为γ和ζ。 1. 计算u= 2. 用集合F对应的原子组成新的观测矩阵XF,判断是否满足式(10),若满足则K0=K0+1,并转入步骤1。否则继续执行算法。 5. 计算式(10),求得满足Epe≥γ的pe值。 7. 更新索引集Λi=Λi(pos(1:pe)),其中pos表示选择前pe个元素。 算法中门限值γ为归一化阈值,其决定了重构信号的比例,0.97≤γ≤0.99。另一个门限值ζ为信道估计误差的允许范围,一般0.1≤ζ≤0.5即可。 对本文提出的NrSAMP算法进行单次重构测试。由图4可以看出NrSAMP算法有较好的重构精度。 图4 NrSAMP算法单次重构测试 为了更清晰地显示NrSAMP算法的优势,将NrSAMP算法与OMP算法、CoSaMP算法、步长为1的SAMP算法、YSAMP算法、VsSAMP算法进行比较。其中高斯稀疏信号的信号长度为256,以固定测量数为128,稀疏度K范围为10到70,对不同的稀疏度进行多次模拟,以计算精确重构概率与信号稀疏度K的关系,所得到的仿真结果如图5所示。分析可知,NrSAMP算法的性能要比同类算法好得多。在同类算法中,OMP和CoSaMP随着稀疏度的逐渐增大而失去对信号的重构效果,但是SAMP及其改进算法和NrSAMP算法仍然保持对信号重构的精度。由于在本次仿真中信号数据较大,稀疏度的取值范围较大,这就证明NrSAMP算法在Massive MIMO系统中进行信道估计是可行的。 图5 不同算法稀疏度K与精确重构概率的关系 将NrSAMP算法应用到Massive MIMO系统中,该系统模型各项参数如表2所示。 表2 Massive MIMO模型参数 续表2 在此Massive MIMO模型中将本文提出的NrSAMP算法与SAMP、CoSaMP、OMP算法在重构精度上进行比较。由图2和图3可知SAMP算法选择初始步长为1,可达到同类SAMP重构精度最大化。故在Massive MIMO信道估计中设置SAMP算法的初始步长为1。得到的结果如图6所示,分析可知,由于NrSAMP算法具有降噪优势,故其在低信噪比情况下能获得比SAMP算法更好的重构率,在高信噪比情况下两者的重构精度相似,二者不论在低信噪比或是高信噪比情况下得到的重构率都比传统的贪婪类算法OMP和CoSaMP得到的重构精度要高。 图6 不同算法在Massive MIMO系统中信道估计的精度 因OMP和CoSaMP算法的稀疏度为已知条件,对每一列接收信号的迭代次数即为这两种算法的稀疏度,故不列入迭代次数的表中,只对NrSAMP和初始步长为1的SAMP算法进行比较,结果如表3所示。 表3 算法迭代次数比较 由表3和图6可以看出,NrSAMP算法在较低的迭代次数下获得的信道估计精度比步长为1时的SAMP算法更高。 本文提出的NrSAMP算法,在应用中能够对信号有较高的重构精度,因此能获得准确的信道估计结果,降低了传统信道估计的复杂度,在同类压缩感知算法中具有降噪的优势。该算法中,迭代次数虽然比步长为1的SAMP算法小,但由于算法在回溯部分是通过迭代次数来保证重构精度,因此后续目标是继续优化原子选择的方法,使算法能保证选出尽可能多的有效原子,在获得高的重构精度的同时,降低算法的运行时间。3 奇异熵理论
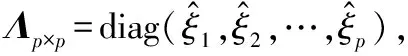
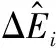
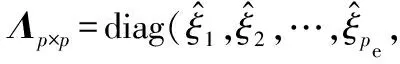
4 Massive MIMO信道估计


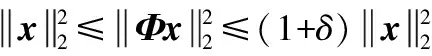


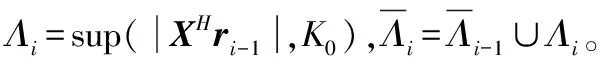
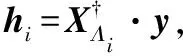

5 实验结果及分析

6 结 语
