考虑货物时间价值的船舶调度多目标优化方法

张安莉，席天为

(重庆师范大学 数学科学学院，重庆 401331)

0 引言

随着世界商贸的飞速发展，利用集装箱船进行商品运输越来越受到国际贸易公司的青睐，成为各大航运企业投资发展的重要领域。在全球提倡低碳经济和绿色航运的背景下，企业能否获得最好经济效益，各航线上船只的调度显得尤为重要。实际运营当中，适当降低船速可以有效减少油耗成本与碳排放成本，因此是船运企业最常用的经营策略。但降低船只航速又会导致运输时间延长，货物的时间价值损失增大。长此以往，由此引发的服务质量水平下降会直接损害航运企业的长期利益。在市场竞争愈发激烈的情况之下，如何兼顾以上因素，科学合理规划船只的调度，实现总利润最大化，是各个航运企业需要面对的重要问题。

目前已有众多学者对船舶的调度问题进行了研究。例如早在上个世纪末，Lane[1]、Ronen[2]及Claessens[3]等学者先后提出了集装箱船只在各航线上的配船优化概念，研究了在航线和货运需求已知的情况下，航运公司的船只调度优化问题。1997年Powell等人[4]利用整数规划模型解决了航运公司的配船问题。2009年Fagerholt[5]以成本最小和船型及发船频次为目标建立了优化模型。随着低碳航运的提出，研究人员逐步将碳排放量纳入研究范围。2009年Corbett等[6]建立了考虑航速的优化模型，研究了碳税对航运公司利润的影响。2013年许欢等[7]建立了以利润最大和碳排放最小为目标的优化模型，并利用智能算法进行求解。2017年 De等[8]将时间窗，吃水限制等影响因素纳入考虑范围，建立了以总利润最大和碳排放总量最小的双目标优化模型。总之大多数学者都是在针对调度问题本身或者是求解算法进行研究[9-15]。值得注意的是，以上研究中均未考虑到货物的时间价值损失[9]。货物的时间价值主要体现在以下几个方面：一是货物本身价值的损失，特别是时间紧或保质期较短的货物最为明显；二是运输时间越长，货物发生损坏的可能性就越大；三是运输时间过长会导致某些类别的货物贬值。关于货物的时间价值的研究主要集中于陆上的交通与物流，在航线船只的调度方面的研究相对来说较少。本文在现有的研究基础上综合考虑，结合航运公司航线上船只调度的生产实际，首先为保证服务质量，提高企业的长期利益，引入货物时间价值概念；再以含碳税成本的总成本最低和货物时间价值损失最小为目标建立了双目标数学模型；其次利用NSGA-Ⅱ算法对模型进行优化求解；最后以某航运企业的数据进行数值实验，证明了模型与算法的可行性与有效性。

1 问题提出

发展低碳经济模式已经成为了航运业的主流趋势。在此背景下，航运业通常考虑通过降低航速来降低含碳税的总成本，而降低航速通常意味着货物的时间价值损失增大，从而影响航运业的长远利益。如何权衡航线上船只的调度是各个航运企业必须做出的选择。基于此，同时考虑含碳税的总成本和货物时间价值损失并建立一个关于船舶调度的多目标优化模型显得尤为重要。

2 模型建立

2.1 模型假设

为建立上述模型，本文作如下基本假设：a) 营运航线及各航线上的货运需求已知；b) 同一航线上船只的发船频率相同；c) 研究期间只考虑航运公司自有船舶，不考虑租赁情况；d) 不考虑研究期间的油价波动；e) 航行时只考虑重油的消耗，停泊在港口时只考虑轻油的消耗。

2.2 符号定义

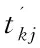
b)决策变量。xkj表示航线j上船型k的营运数量；vkj表示航线j上船型k的船速；Ok表示船型k的闲置数量。

2.3 模型建立

2.3.1 年运营总成本

航运公司的年运营总成本包括了船只的闲置成本，航行的固定成本(包括船员工资成本，维修成本，管理成本，物料成本等)，油耗成本，以及碳税成本。其中，船型k的闲置成本为Fk，船型k的闲置数量为Ok，则船只的闲置成本为：

单船k航行的固定成本Ckj，航线j上的k型船只数量为xkj，则船只的固定成本为：

油耗成本包括两部分：航行时的油耗成本与停泊时的油耗成本。其中航行时的天数可表示为

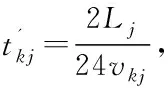
碳税成本是税率e、碳排放因子以及燃料排放量这三者的乘积，其中航行时重油的碳排放因子为θ1，停泊在港口时轻油的碳排放因子为θ2，则碳税成本为

于是年运营总成本为F=A+B+C+D。

2.3.2 货物时间价值损失

货物的时间价值损失主要是与运输时间有关，当运输时间越短时，货物的时间价值损失越小。单次运输的货物时间价值损失可由如下公式求得：

2.3.3 本文模型

基于上述分析，本文的多目标数学模型如下：

minF，

(1)

(2)

s.t.

(3)

(4)

(5)

(6)

(7)

xkj≥0,∀k∈K,∀j∈J,

(8)

Ok≥0,∀k∈K。

(9)

其中：式(1)为第一个目标函数，表示运营所需的总成本；式(2)为第二个目标函数，表示货物的时间价值损失；式(3)表示各航线上配备的船只发班数量不少于计划班次，式(4)表示满足各航线的货运需求，式(5)表示某船型船只分配在各航线上的数量与其闲置数量之和等于该船型的总数量，式(6)表示保证所有的船型的船只量之和与船只总拥有量相同，式(7)表示各航线上船舶的航速限制，式(8-9)保证决策变量的非负性。

3 模型求解算法

3.1 模型算法分析

由于上文中构建的多目标数学模型的决策变量中既有整数型变量，又有连续型变量，而且模型中存在非线性关系，因此该模型为一个多目标混合整数非线性规划模型。本文将采用带有精英策略的快速非支配排序遗传算法(NSGA-Ⅱ)进行求解。

3.2 NSGA-Ⅱ算法

Step1：实数编码的方式随机生成初始种群N，经过非支配排序与拥挤度计算后，再通过遗传、交叉、变异三个基本操作得到第一代子代种群；

Step2：从第二代开始，将父代种群与子代种群进行合并，然后进行快速非支配排序，同时对各非支配层中的个体进行拥挤度计算，根据非支配关系与拥挤度选取合适的个体组成新的父代种群；

Step3：通过遗传算法的基本步骤产生新的子代种群，重复以上步骤，直到满足程序结束的条件为止。算法流程图如图1所示。

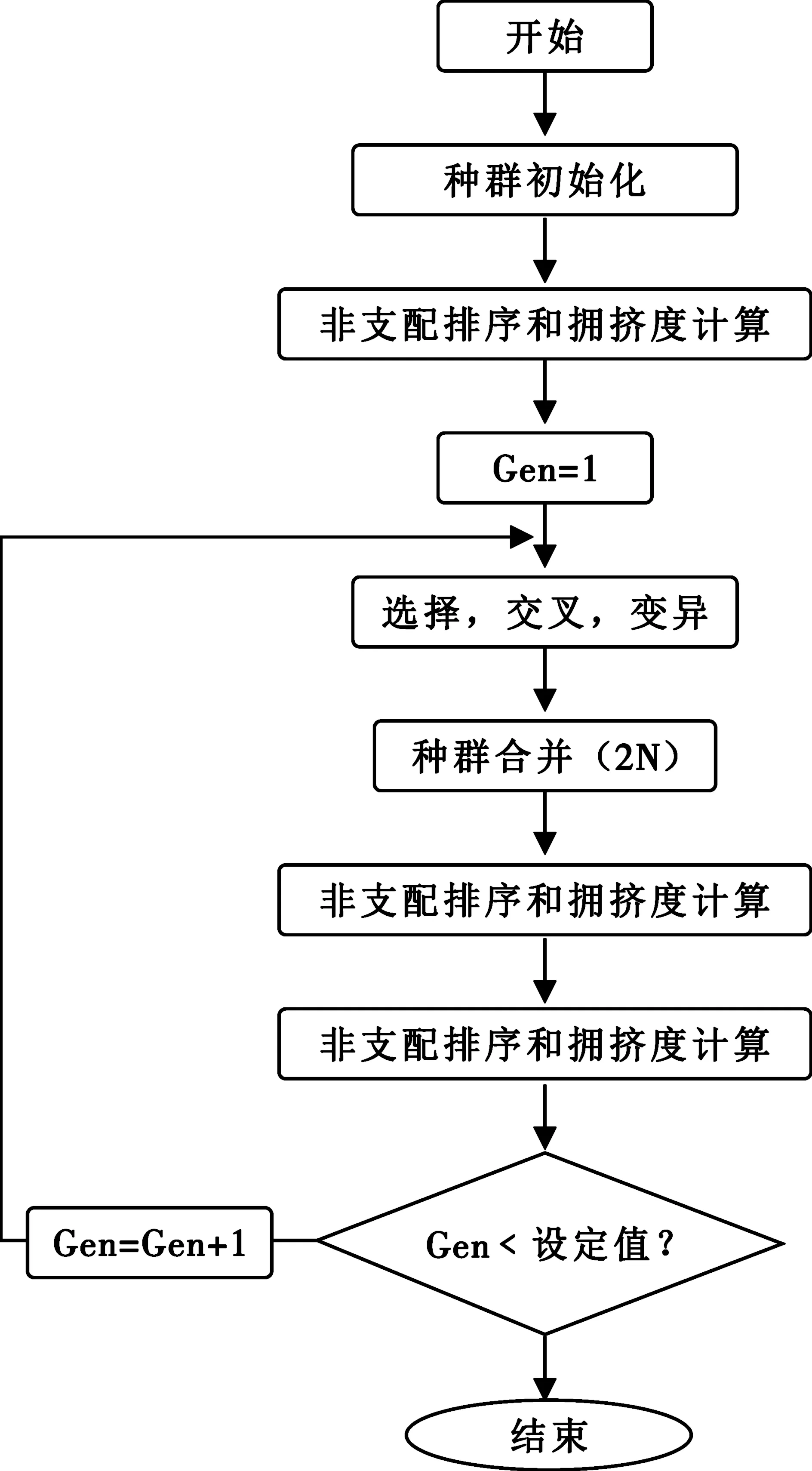
图1 NSGA-Ⅱ算法流程

4 数值实验

4.1 基础数据

现有某航运企业计划根据航线上的实际情况设计船只的调度方案。该企业有3种船型，共23条船，运营3条航线，所有船舶的年运营时间均为342天，其他数据信息如表1-表4[15]。并假设所有船型的航速范围均在[14,25]之间；重油的价格Pr为185美元/吨；轻油的价格Pc为310美元/吨；航行时的碳排放系数θ1为3.114；港口的碳排放系数θ2为3.206；税率e为5。单位集装箱货物的价值Vf为30万美元；年货物持有成本系数ρ为20%。

表1 船舶航线信息

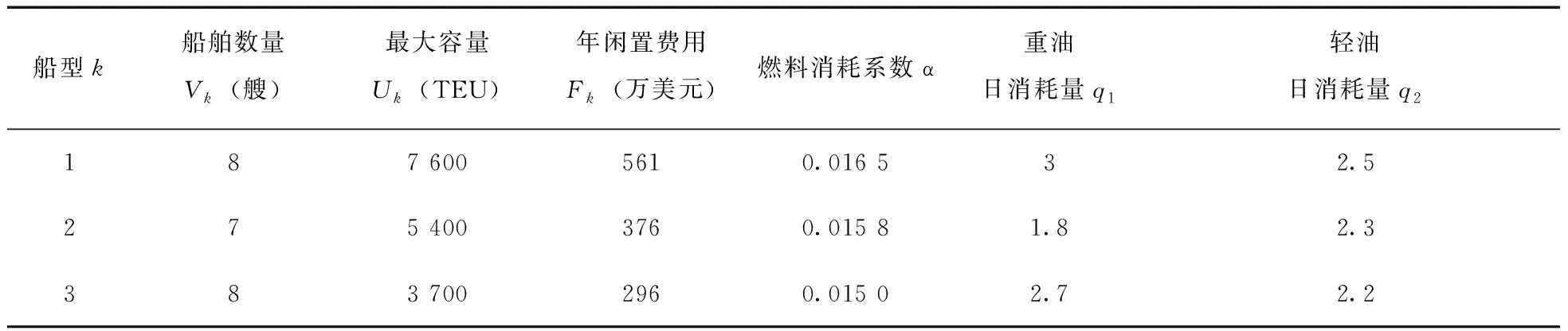
表2 船舶数据

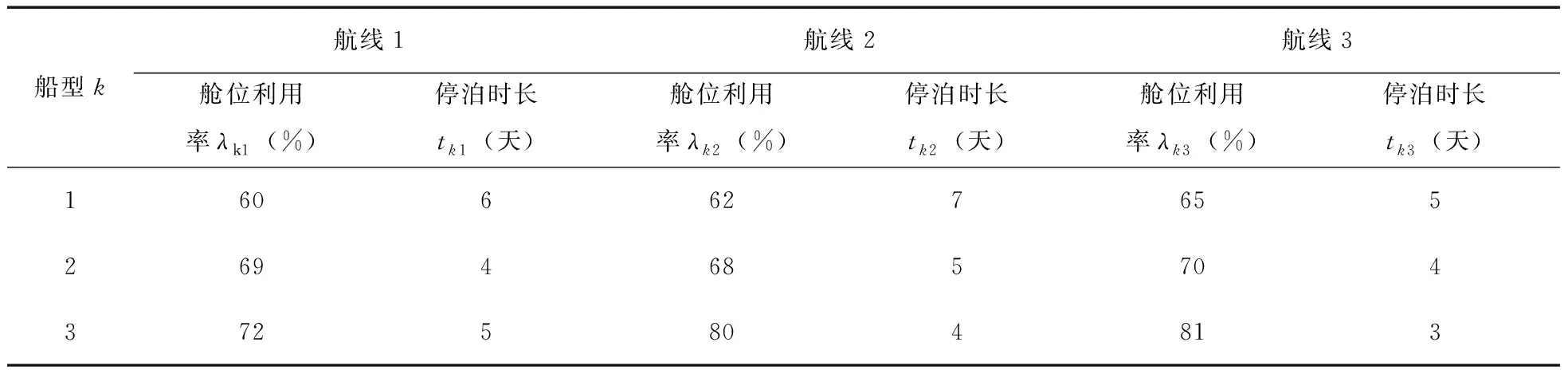
表3 各航线各船型装载率与停泊时长

表4 年运营成本

4.2 方案优化

利用MATLAB编程，采用NSGA-Ⅱ算法，取种群数量N=50，交叉率为0.6，变异率为0.1，迭代次数为2000，得到20个同时满足要求的pareto解(见表5)。

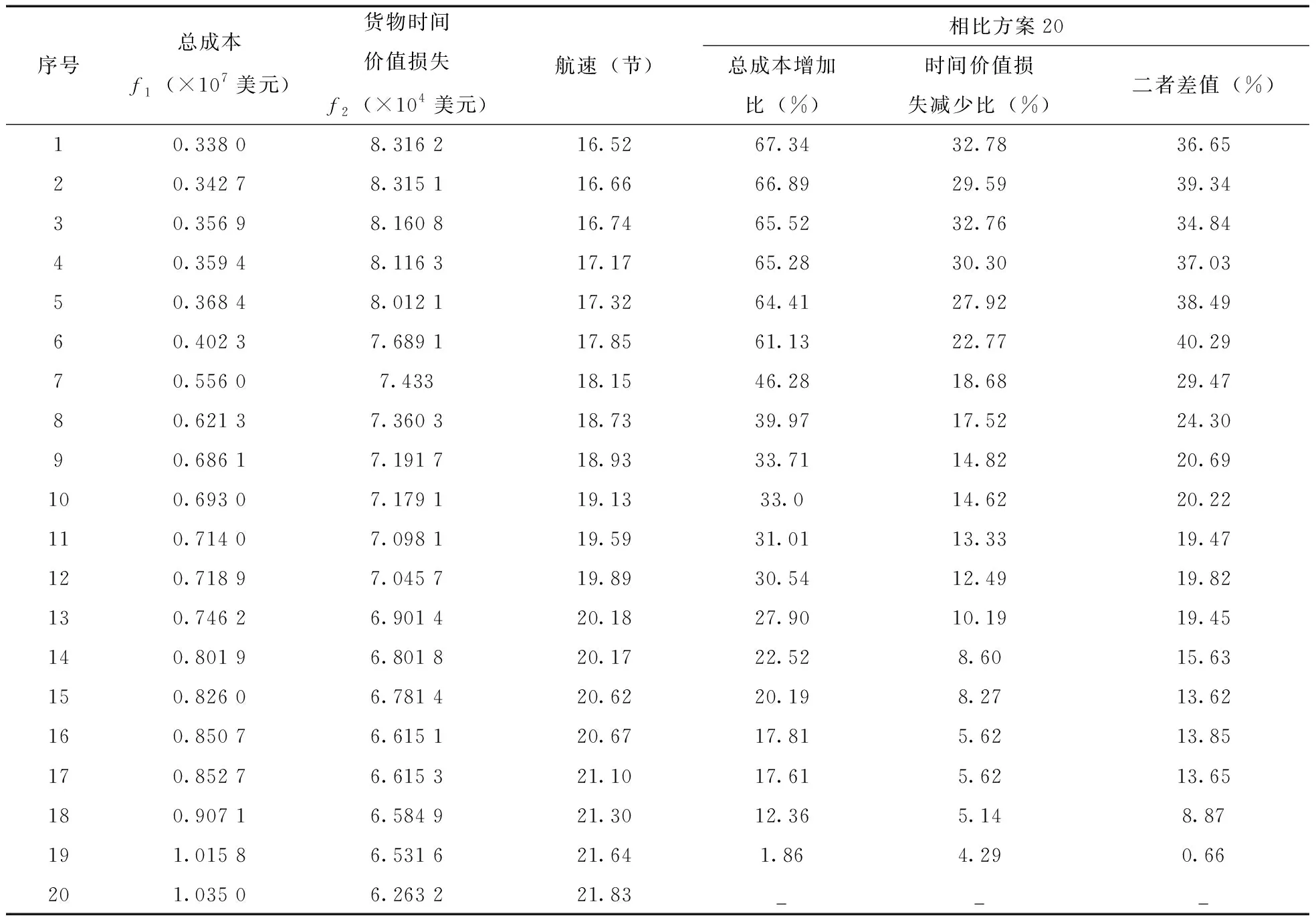
表5 Pareto解集对应的参数表

由表5可知，当各船只的平均航速越大时，总成本越高，货物时间价值损失越低。如表5中的方案6的总成本为4023万美元，货物时间价值损失为76 891美元，相比于其他方案，如方案20，虽然货物时间价值损失变高了22.77%，但总成本减少了61.13%，并且二者差值达到最高为40.29%。若在市场低迷时，方案6也不失为一个最佳的方案，方案6具体可见表6和表7。

表6 船只调度数量方案

表7 各航线的航速

4.3 碳税变化的影响

碳税税率变化对船只航速与数量的影响，见图2及图3。

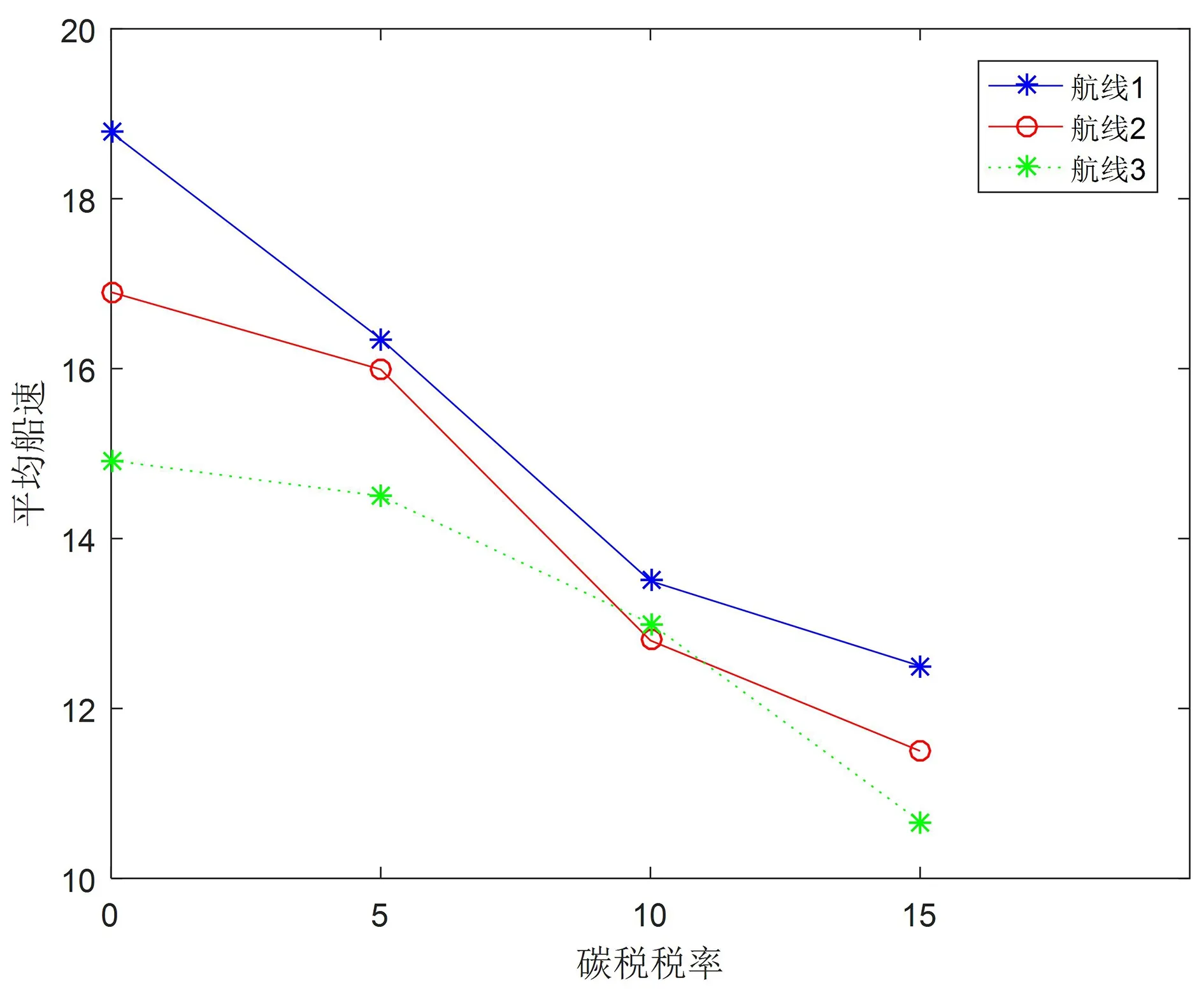
图2 各航线上船只船速的变化

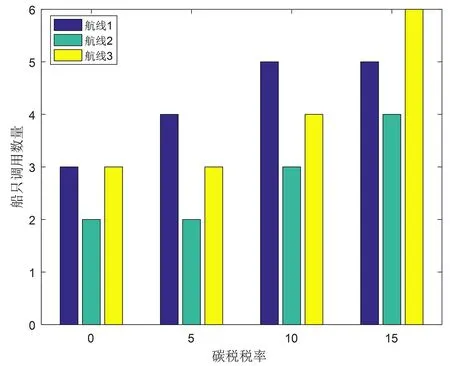
图3 各航线上运营船只数量的变化

由图2可以看出，当税率提高时，各航线上的平均船速均呈下降趋势。由图3可知，随着税率的增高，各航线上的运营船只数量也呈增加趋势。说明当碳税增加到一定程度时，船运企业为降低运营成本不得不通过降低船速来控制碳税成本，同时为了保证货物价值需投入更多的船只。

4.4 货物时间价值变化的影响

各类货物(如汽车零件，时装，食品，茶叶等)的持有损失率各不同。由此分别取1%、5%、10%、15%和25%共5种损失率进行分析，见图4。

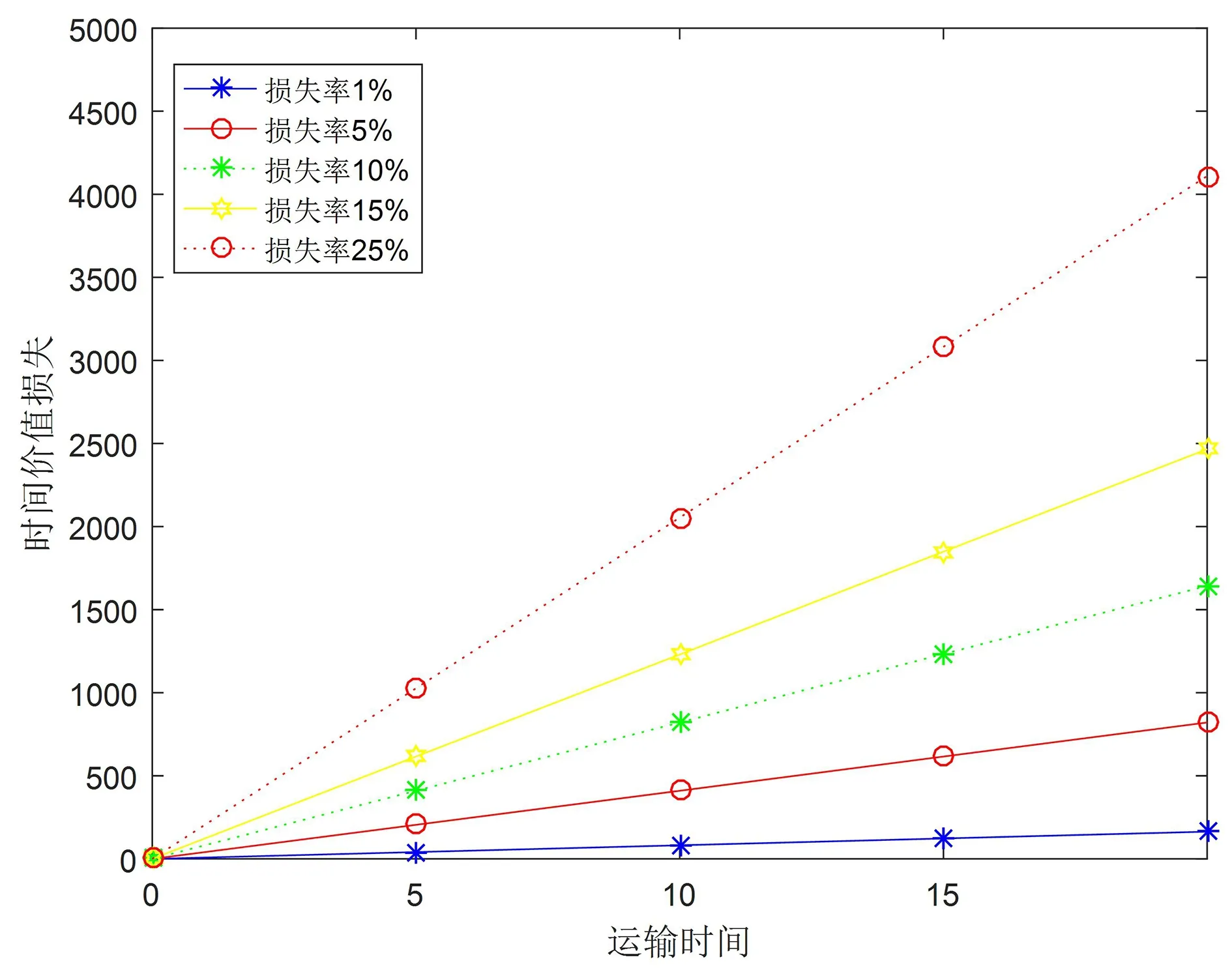
图4 货物时间价值损失变化

由图4可以看出，对于高损失率的货物，运输时间过长会急剧地导致损失变大。在绿色航运要求的范围内，当货物属性明确时，若遇到高价值损失货物则必须优先考虑货物运输时间损失，其次考虑运营总成本。若是低价值损失货物，可优先考虑含碳成本的总成本。

综上，决策者可以根据市场状况和企业战略目标科学地选择方案。当市场需求低迷且货物损失率较低的时候，航运企业可以优先考虑成本因素，适当降低航速；当市场需求良好的情况下，航运公司可以优先考虑货物时间价值损失，保证服务质量水平，提高企业的市场竞争力，适当提高航速。

5 结论

本文针对航运企业集装箱船只的调度问题，建立了以运营总成本(包含碳排放成本)最小和货物时间价值损失最小为目标的多目标优化模型，并利用NSGA-Ⅱ算法对模型进行了求解，最后以某航运企业航线上的数据进行了数值实验，验证了文中提出的优化思路和算法在解决实际问题当中的有效性，取得了满足要求的pareto解集。企业决策者可以根据航运市场实际状况和企业战略目标从中选择科学合适的方案。值得注意的是，影响船舶调度的因素还有很多，比如实际航行当中船只的吃水限制，港口的时间窗口限制等，因此方案还需要进一步优化，基于以上情况的航线调度优化方案将是下一步需要研究的课题。