基于双向2DPCA算法的高分五号卫星图像降维研究
2021-01-14何春,郭科
何 春,郭 科
(1.西华师范大学 教育信息技术中心,四川 南充637009;2.数学地质四川省重点实验室(成都理工大学),四川 成都610059)
0 引言
随着遥感技术的不断发展,高光谱图像的光谱分辨率可达纳米数量级,在获得地物图像信息的同时,也获得其丰富的光谱信息,真正做到了图像与光谱的结合,具有图谱合一的重要特性[1]。高光谱图像具有光谱分辨率高、波段多、相邻波段间互相关性强等特点。但是,由于高光谱图像的波段众多,波段数据之间势必存在大量冗余。庞大的数据量对图像的存储、传输和处理造成了很多困难。为了更好地实现高光谱图像的地物识别和分类等应用目的,其数据的预处理过程就显得尤为重要[2],保留重要信息、去除图像噪声和减少数据冗余是预处理的主要目的。
主成分分析(PCA)已在高光谱遥感领域得到了广泛应用,是一种常见的对高光谱数据进行降维的处理方法,但其在降维时,需要先将波段图像转换成一维向量,这样不但会破坏图像的结构信息,还由于维度的增加,加大了计算量[3]。2004年,Yang Jian等[4]提出了二维主成分分析(2DPCA),它无需将波段图像转换成一维向量,直接利用二维图像矩阵提取特征,既保留了图像的结构信息,也使计算时间大大缩短。但是2DPCA只是在图像矩阵的行方向上提取特征,降低维数,而忽略了对列方向的操作,导致其降维效果还不够理想。针对上述问题,Zhang等[5]在2005年提出了双向2DPCA算法((2D)2PCA),该方法在图像的行和列方向上同时进行二维主成分分析,即同时降低了图像矩阵在行和列方向上的维数,其降维效果得到了极大的提升。
然而,双向2DPCA方法在高光谱图像降维中的应用却见刊极少,目前对高分五号卫星图像的研究也相对较少。本文拟将双向2DPCA降维算法应用于高分五号卫星图像,既是为检验该算法对高分五号卫星图像的降维性能,同时也为该卫星图像的后续处理做好准备。实验证明,双向2DPCA算法对于高分五号卫星图像具有极好的降维效果。
1 双向2DPCA算法
1.1 二维主成分分析(2DPCA)
假设某高光谱遥感图像A具有p个波段(A1,A2,…,Ap),图像矩阵尺寸为m×n像素。X∈Rn×n1(n≥n1)是由相互正交的列向量组成的投影矩阵,将图像矩阵A通过Score=AX的线性变换投影到X上,得到m×n1的矩阵Score,Score即为图像A在X上的投影特征矩阵,X即为投影矩阵,2DPCA的思想就是寻找最优投影矩阵[6]。算法步骤如下:
(1)
b)计算高光谱图像A在行方向上的协方差矩阵C1(维度为n×n):
(2)
c)求解协方差矩阵C1的特征值和特征向量,选择C1的前n1个最大特征值λ1,λ2,…,λn1,以及对应的特征向量X1,X2,…,Xn1,则X=[X1,X2,…,Xn1]即是最优的投影矩阵(维度为n×n1)。
d)将各波段图像Ai(i=1,2,…,p)投影到投影矩阵X上,得到各波段图像在行方向上的主成分,也即投影特征矩阵Scorei(维度为m×n1):
Scorei=AiX。
(3)
1.2 双向二维主成分分析((2D)2PCA)
二维主成分分析只是在图像矩阵的行方向对数据进行分析,即对p个m×n样本矩阵从行方向降维后,得到投影矩阵X=[X1,X2,…,Xn1],以及样本的投影特征矩阵Scorei=AiX(i=1,2,…,p)。这样,m×n的图像矩阵降维到了m×n1(n≥n1)[7]。双向二维主成分分析继续对样本矩阵的列方向进行降维分析,同理得到投影矩阵Y=[Y1,Y2,…,Yn2] ,以及样本的特征矩阵Si=YTScorei=YTAiX(i=1,2,…,p)。这样,m×n的图像矩阵降维到了n2×n1(m≥n2,n≥n1)。算法步骤如下:
ɑ)计算高光谱图像A在列方向上的协方差矩阵C2(维度为m×m):
(4)
b)求解协方差矩阵C2的特征值和特征向量,选择C2的前n2个最大特征值λ1,λ2,…,λn2,以及对应的特征向量Y1,Y2,…,Yn2,则Y=[Y1,Y2,…,Yn2]即是最优的投影矩阵(维度为m×n2)。
c)将各波段图像Ai(i=1,2,…,p)同时投影到投影矩阵Y和X上,得到各波段图像在行和列方向上的主成分,也即投影特征矩阵Si(维度为n2×n1):
Si=YTScorei=YTAiX。(i=1,2,…,p)
(5)
d)提取了各波段图像矩阵在行、列方向上的主成分Si后,可以通过下式重构每个波段的图像Bi:
Bi=YSiXT=YYTAiXXT。 (i=1,2,…,p)。
(6)
相比2DPCA,(2D)2PCA进一步将图像矩阵m×n的主成分从m×n1(n≥n1)压缩到了n2×n1(m≥n2,n≥n1),从而实现了在行和列上都对图像数据进行了降维[8]。
1.3 算法评价
对高光谱遥感图像A进行了降维后,可以通过图像信息保持率μ(等同于特征值的累计贡献率)、图像压缩率φ以及峰值信噪比PSNR三个指标对其降维性能进行评价[9]。
a)图像信息保持率(μ1表示行方向上特征值的累计贡献率,μ2表示列方向上特征值的累计贡献率)
(7)
b)图像压缩率
(8)
对于高光谱图像而言,波段数值p一般都比较大,在这种情况下,图像压缩率φ可用
近似代替。
c)峰值信噪比(PSNR)
图像在经过压缩处理之后,输出的图像都会在某些程度上与原始图像不同,峰值信噪比就是用来评价一幅图像压缩后和原图像相比质量的好坏,单位为dB。PSNR值越高,图像压缩后失真越小,其有效信息保留越多[10],反之亦然。在本文中,使用峰值信噪比对经过主成分提取后重构的波段图像与原图像进行评价和对比。
对于一幅大小为m×n的原始图像A和经过降维处理后的图像B,PSNR的计算公式为:
(9)
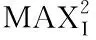
(10)
2 实验及分析
2.1 实验环境及图像
本文实验软件环境为MATLAB R2014a以及ENVI Classic 5.1。
本文采用的高光谱图像来源于高分五号卫星图像。高分五号卫星于2018年5月9日在我国太原卫星发射中心成功发射, 作为全球首颗大气和陆地综合高光谱观测卫星,高分五号卫星 “上可看大气、中可观地表、下可探地矿”,同时高分五号也是世界上第一颗能对陆地和大气进行综合观测的卫星[11]。本文研究的图像尺寸为361×429像素,具有330个波段。拍摄地点位于我国东北某地。下图1为该遥感图像的真彩色显示。

图1 实验图像
2.2 实验结果及分析
在对330个波段图像提取了行和列的主成分后,通过特征值的累计贡献率可以看出,行和列的第1主成分就包含了原图像85%的信息。429个行主成分中,前167个主成分包含了原图像99%的信息;361个列主成分中,前123个主成分包含了原图像99%的信息。表1列举了行和列的前1~10个主成分所包含的图像信息比例。图2提供了行列主成分包含的信息保持率趋势图。从趋势图可以看出,行和列前面的主成分都已包含了图像的绝大部分信息,后面的主成分对图像信息贡献极小,趋势也逐渐平缓。

表1 行和列前1~10个主成分包含的图像信息保持率(%)
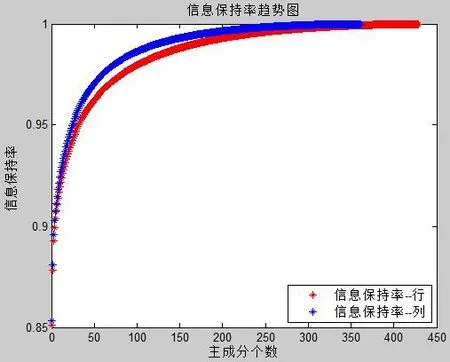
图2 行列主成分信息保持率趋势图
为了获得更详细的降维数据和结果,表2 对比分析了2DPCA算法以及双向2DPCA算法,给出了不同信息保持率对应的主成分大小以及图像压缩率的具体数值。从表中可以看到,随着信息保持率的增加,两种算法的主成分尺寸以及对应的图像压缩率均在逐渐变大,但是在相同的信息保持率下,双向2DPCA算法的主成分尺寸小于2DPCA算法,其对应的图像压缩率也远远小于2DPCA算法。这是因为2DPCA仅仅对图像的列进行降维,而行并没有改变,故主成分尺寸更大,其图像压缩率也更大。这也证明了双向2DPCA算法的降维能力更强。同时从表中可以看到,即使是信息保持率高达99.9%时,双向2DPCA算法的主成分尺寸也能够降维到274×341,对应的图像压缩率只有60.33%,而2DPCA算法的图像压缩率高达79.49%,这表明双向2DPCA算法的降维效果极好,能够大大节省计算机存储数据的空间,极其有利于对数据的后期处理。
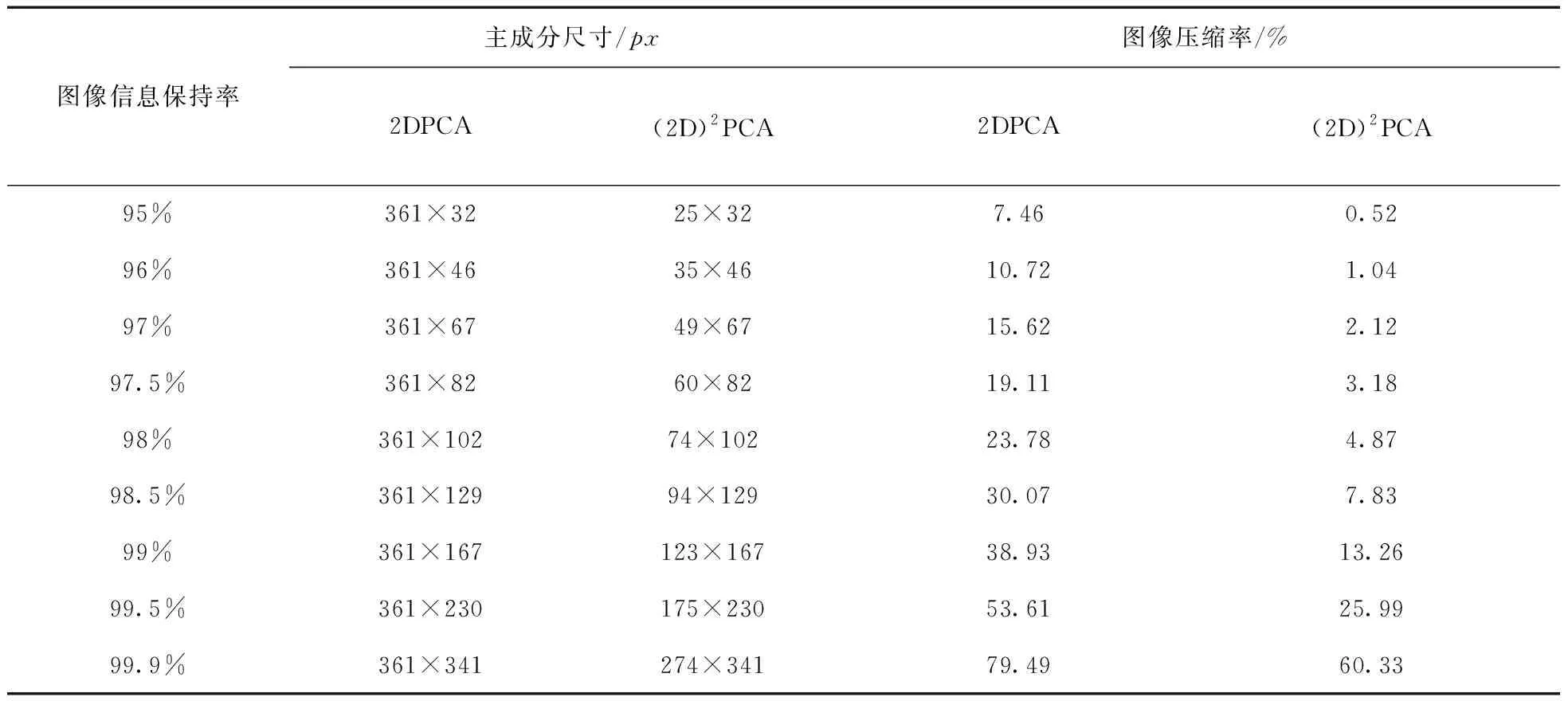
表2 2DPCA算法与双向2DPCA算法的降维效果对比
在提取了主成分后,需要对波段图像进行重构。由于高光谱图像波段较多,故本实验从330个波段图像中选取了5个噪声小、图像表现较好的波段进行图像重构,分别是第90、120、150、180、210波段。表3继续对比分析了2DPCA算法以及双向2DPCA算法,显示了这5个波段分别在信息保持率为98%、99%、99.9%时,原图像与重构图像的峰值信噪比。从表3可以看出,两种算法的共同趋势是,这5个波段在相同信息保持率下的PSNR值比较接近,而同一波段的PSNR值随信息保持率的增加而增加,这证明了信息保持率越高,所提取的主成分就越多,获取的图像有效信息也就越多,那么相应的PSNR值也就越高[12]。同时,从表中数据对比可以看出,在相同的信息保持率下,5个波段对应的2DPCA算法的PSNR值均略高于双向2DPCA算法,这是因为2DPCA算法的主成分尺寸更大,图像压缩率更高。然而用比双向2DPCA算法大得多的主成分尺寸和图像压缩率来换取只比双向2DPCA算法略高的PSNR值,再次证明双向2DPCA算法的降维性能远远超出2DPCA算法。
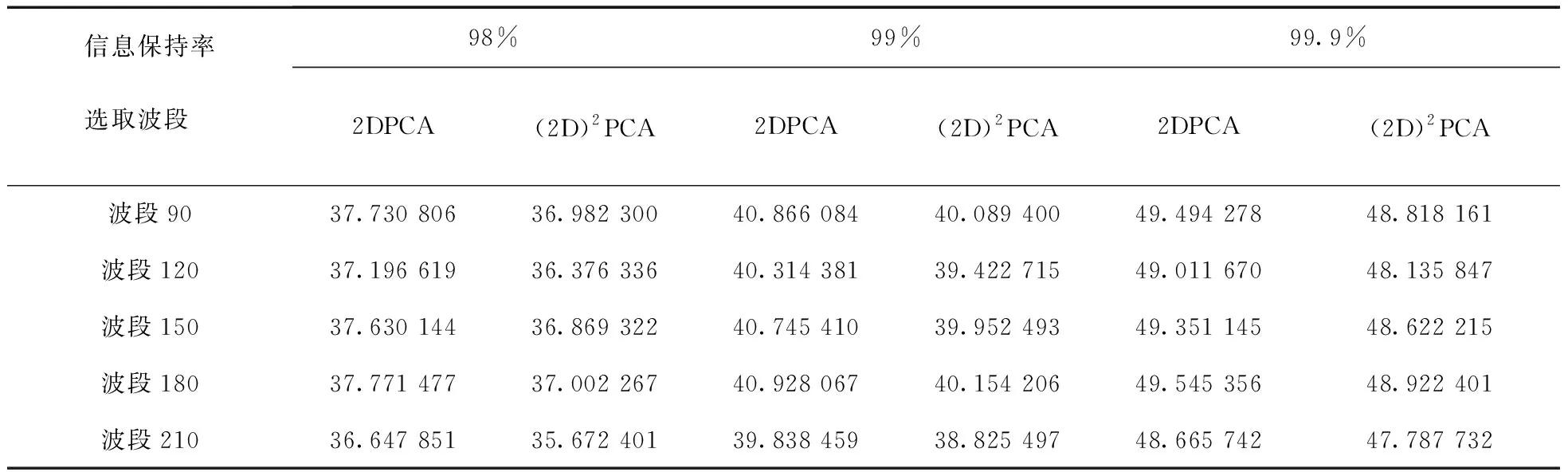
表3 2DPCA算法与双向2DPCA算法在不同信息保持率下的PSNR对比(dB)
图3~图7分别显示了这5个波段的原图像以及利用2DPCA算法和双向2DPCA算法在信息保持率为98%和99.9%时对其重构的图像。从各波段原图像可以看出,波段90的灰度变化较多,结构比较复杂,具有更多的细节信息,而波段210灰度变化较少、过渡比较平稳,图像整体结构较为简单,相对提供的细节信息更少。
当信息保持率为98%时,可以看出两种算法的重构图像其整体清晰度都不高,图像的大部分细节和纹理信息都已丢失。其中2DPCA算法的重构图像充斥着竖条纹,双向2DPCA算法的重构图像则充斥着横竖条纹,这是因为2DPCA算法只对图像的行向量进行降维,故经降维重构后的图像在行方向上会丢失一些信息,导致图像中出现了竖条纹,而双向2DPCA算法同时对行和列进行降维,所以其重构图像在行和列方向上都会丢失一些信息,故图像会出现横竖条纹。在5个波段中,第90波段的条纹最多,第210波段的条纹相对最少。而从表3数据得知,当信息保持率为98%时,两种算法在波段90的PSNR值均比波段210稍高一些。出现这种情况是因为2DPCA算法和双向2DPCA算法的图像重构效果和图像压缩率都对遥感图像的灰度值比较敏感[13],对于灰度变化较多,灰度值变化范围较大的图像重构效果相对较差,而对灰度值变化范围小,图像结构更为简单的图像重构效果相对较好。
当信息保持率为99.9%时,两种算法的5张重构图像都能较好的保留地物的边缘和纹理信息,图像中的条纹明显减少,其中又以图像结构较为简单的210波段重构图像效果最好。从肉眼判断两种算法的重构效果基本一致。在2DPCA算法与双向2DPCA算法的处理过程中,图像的大部分低频信息集中在前面的主成分中,而大部分高频信息集中在后面的主成分中[14]。地物的边缘和纹理属于高频信息,所以相较于98%的信息保持率而言,99.9%的信息保持率提取了更多的高频主成分,所以其重构图像能够较好的保持地物的边缘和纹理信息[15],图像整体更为清晰、干净,对原图像的还原能力更强。

图3 选取波段的原图像

图4 2DPCA算法在信息保持率为98%时的重构图像

图5 双向2DPCA算法在信息保持率为98%时的重构图像

图6 2DPCA算法在信息保持率为99.9%时的重构图像

图7 双向2DPCA算法在信息保持率为99.9%时的重构图像
3 结论
本文通过对2DPCA算法与双向2DPCA算法的实验比较,对高分五号卫星图像进行了降维研究,结论如下:
在行和列方向上,双向2DPCA算法提取的第1主成分均能包含原图像85%的信息,行方向39%的主成分以及列方向34%的主成分就能包含原图像99%的信息。主成分提取后对应的图像压缩率比较低,有效的节省了数据存储的空间,同时充分说明了所提取主成分的高效性。另外,重构图像的PSNR值也比较理想。
由于双向2DPCA算法需要计算图像数据的协方差的特性,导致了该算法对图像的灰度值变化范围比较敏感。相对而言,灰度值变化范围较小的波段,其图像重构效果更好。由于图像的高频信息更多集中在提取主成分的后半部分,故较大信息保持率对应的重构图像能更好的保留其边缘和纹理信息,图像整体更为清晰。
总体而言,双向2DPCA算法对于高分五号卫星图像降维的效果比较好,具有普适性,可以推广应用于其他高分五号卫星图像。
