数学问题解答

2020年10月号问题解答

(解答由问题提供人给出)

2566如图，等腰△PAB中，PA=PB,过三角形中一点O作直线交边PA,PB于点E,F(不同于A,B)，使AE=OE,BF=OF.直线AO与PB交点为N,直线BO与PA交点为M,直线MF与NE交点为Q,直线AF与BE交点为R.求证：P,Q,R三点共线.

(山东省泰安市宁阳第一中学 刘才华 271400)

证明直线MB割△PEF三边所在直线于点M,O,B,

又PA=PB，AE=OE,BF=OF，

由塞瓦定理逆定理得直线PO,EN,FM三线相交于点Q,则P,Q,O三点共线.

(1)

设PO与AB交于点D,

∠APD=α,∠BPD=β.

在△PEF中,

在△PAB中,

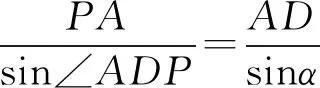
由塞瓦定理逆定理得直线PD,AF,BE三线相交于点R,则P,D,R三点共线.

(2)

由(1)、(2)及P,O,D三点共线得P,Q,R三点共线.

2567已知a,b,c>0,求证：

(陕西省咸阳师范学院基础教育课程研究中心 安振平 712000)

证明因为a2+b2+c2≥ab+bc+ca,

所以 (a+b+c)2≥3(ab+bc+ca).

据此，并应用柯西不等式，得

令x=a+b+c,只要证

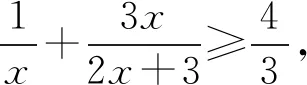
2568以任意三角形各边为底边分别向外侧作同向相似的三角形，则位于外侧的三个顶点构成的三角形与原三角形重心重合．

(湖北省公安县第一中学 杨先义 434300)

证明如图，三角形外三个相似三角形的两个内角分别记为α,β，设A(x1,y1)，B(x2,y2)，C(x3,y3)，现求D(xD,yD)．

由于图形中仅有有限条线段，因此，不妨设所有线段的斜率都存在．

当α,β都不是直角时，由夹角公式得

同理

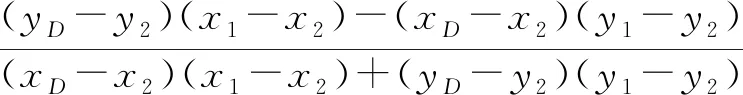
解之得

类此可得到

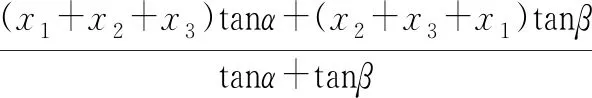
=x1+x2+x3，

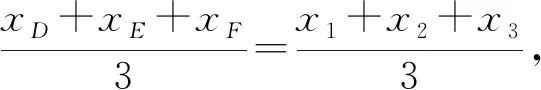
所以△ABC与△DEF的重心重合．

当α,β中有一个为直角(例如β为直角)时，有

解之得xD=x2+(y2-y1)tanα，

yD=y2+(x1-x2)tanα，

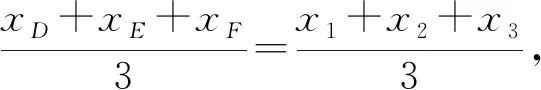
所以△ABC与△DEF的重心重合．

(河南省方城县教研室 邵明宪 473200)

2570如图，已知I是△ABC的内心，点G是∠B相对的旁心，D是BC边的中点，DI交AC于点F，求证：CF=GF.

(北京市陈经纶中学 龚浩生 100020)

证明因为I是内心，G是旁心，

所以B,I,G三点共线.

连结BG，交AC于E，连结GC，延长BC到T.

由DIF截△BCE，根据梅涅劳斯定理，得

①

又AI,AG分别是△ABC的内角平分线和外角平分线，

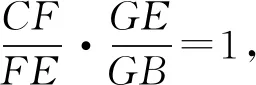
所以FG//BC，

所以∠FGC=∠GCT=∠FCG，

所以CF=GF.

2020年11月号问题

(来稿请注明出处——编者)

2571在△ABC中，试证：

(浙江湖州市双林中学 李建潮 周秋斓 313012)

2572已知⊙O是△ABC的外接圆(如图)，E,F分别是两边AB,AC的中点；CM，BN分别是AB，AC边上的高，相交于点H；EF，MN交于点P,联结AP，OH.求证：AP⊥OH.

(江西省高安市石脑二中 王典辉 330818)

2573已知实数a,b,c,d>0，且a+b+c+d=1，求证：

(重庆三峡学院数学与统计学院 陈晓春 404000)

2574设k为正整数,求证不定方程4kx2-y2=1无整数解.

(天津水运高级技工学校 黄兆麟 300456)

(江苏省海门中学 徐巧石 226100)